2.4. التجميع الثنائي#

تقوم خوارزميات التجميع الثنائي بتجميع صفوف وأعمدة مصفوفة البيانات في وقت واحد. تُعرف مجموعات الصفوف والأعمدة هذه باسم التجميعات الثنائية. يحدد كل منها مصفوفة فرعية من مصفوفة البيانات الأصلية ببعض الخصائص المطلوبة.

على سبيل المثال، بالنظر إلى مصفوفة من الشكل (10، 10)، فإن أحد التجميعات الثنائية المحتملة بثلاثة صفوف وعمودين يحث مصفوفة فرعية من الشكل (3، 2):

>>> import numpy as np
>>> data = np.arange(100).reshape(10, 10)
>>> rows = np.array([0, 2, 3])[:, np.newaxis]
>>> columns = np.array([1, 2])
>>> data[rows, columns]
array([[ 1,  2],
       [21, 22],
       [31, 32]])

لأغراض التصور، بالنظر إلى التجميع الثنائي، قد يتم إعادة ترتيب صفوف وأعمدة مصفوفة البيانات لجعل التجميع الثنائي متجاورًا.

تختلف الخوارزميات في كيفية تعريف التجميعات الثنائية. بعض الأنواع الشائعة تشمل:

  • قيم ثابتة أو صفوف ثابتة أو أعمدة ثابتة

  • قيم عالية أو منخفضة بشكل غير عادي

  • مصفوفات فرعية ذات تباين منخفض

  • صفوف أو أعمدة مترابطة

تختلف الخوارزميات أيضًا في كيفية تعيين الصفوف والأعمدة للتجميعات الثنائية، مما يؤدي إلى هياكل تجميع ثنائي مختلفة. تحدث هياكل الكتل القطرية أو رقعة الشطرنج عندما يتم تقسيم الصفوف والأعمدة إلى أقسام.

إذا كان كل صف وكل عمود ينتمي إلى مجموعة ثنائية واحدة بالضبط، فإن إعادة ترتيب صفوف وأعمدة مصفوفة البيانات تكشف عن التجميعات الثنائية على القطر. فيما يلي مثال على هذا الهيكل حيث تحتوي التجميعات الثنائية على قيم متوسطة أعلى من الصفوف والأعمدة الأخرى:

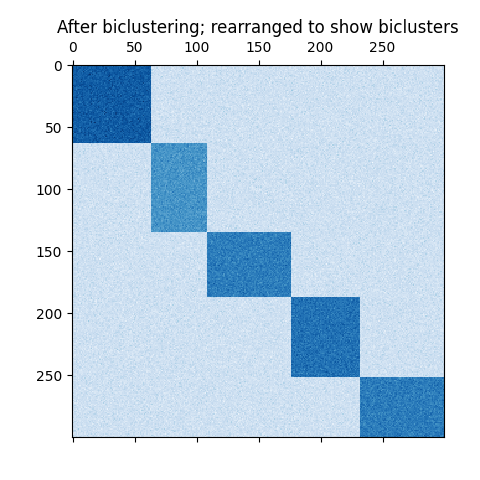
../_images/sphx_glr_plot_spectral_coclustering_003.png

مثال على التجميعات الثنائية التي تم تشكيلها عن طريق تقسيم الصفوف والأعمدة.#

في حالة رقعة الشطرنج، ينتمي كل صف إلى جميع مجموعات الأعمدة، وينتمي كل عمود إلى جميع مجموعات الصفوف. فيما يلي مثال على هذا الهيكل حيث يكون تباين القيم داخل كل مجموعة ثنائية صغيرًا:

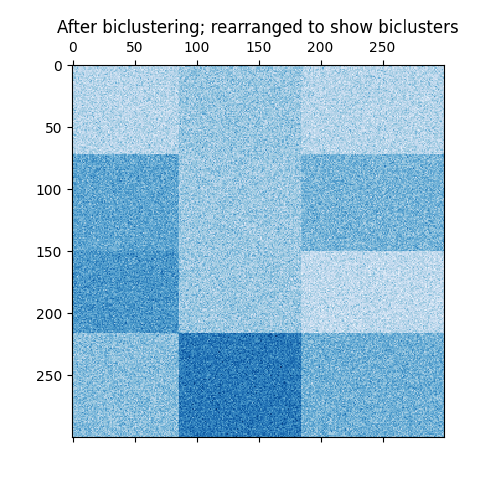
../_images/sphx_glr_plot_spectral_biclustering_003.png

مثال على التجميعات الثنائية رقعة الشطرنج.#

بعد ملاءمة نموذج، يمكن العثور على عضوية مجموعة الصفوف والأعمدة في سمات rows_ و columns_. rows_[i] هو متجه ثنائي مع إدخالات غير صفرية تقابل الصفوف التي تنتمي إلى التجميع الثنائي i. وبالمثل، يشير columns_[i] إلى الأعمدة التي تنتمي إلى التجميع الثنائي i.

تحتوي بعض النماذج أيضًا على سمات row_labels_ و column_labels_. تقسم هذه النماذج الصفوف والأعمدة، كما هو الحال في هياكل التجميع الثنائي للكتل القطرية ورقعة الشطرنج.

ملاحظة

للتجميع الثنائي العديد من الأسماء الأخرى في مجالات مختلفة بما في ذلك التجميع المشترك، والتجميع ثنائي الوضع، والتجميع ثنائي الاتجاه، والتجميع الكتلي، والتجميع ثنائي الاتجاه المقترن، إلخ. تعكس أسماء بعض الخوارزميات، مثل خوارزمية التجميع المشترك الطيفي، هذه الأسماء البديلة.

2.4.1. التجميع المشترك الطيفي#

تجد خوارزمية SpectralCoclustering مجموعات ثنائية ذات قيم أعلى من تلك الموجودة في الصفوف والأعمدة الأخرى المقابلة. ينتمي كل صف وكل عمود إلى مجموعة ثنائية واحدة بالضبط، لذا فإن إعادة ترتيب الصفوف والأعمدة لجعل الأقسام متجاورة يكشف عن هذه القيم العالية على طول القطر:

ملاحظة

تعامل الخوارزمية مصفوفة بيانات الإدخال على أنها رسم بياني ثنائي: تتوافق صفوف وأعمدة المصفوفة مع مجموعتي الرؤوس، ويتوافق كل إدخال مع حافة بين صف وعمود. تقوم الخوارزمية بتقريب القطع الطبيعي لهذا الرسم البياني للعثور على رسوم بيانية فرعية ثقيلة.

2.4.1.1. الصيغة الرياضية#

يمكن إيجاد حل تقريبي للقطع الطبيعي الأمثل من خلال تحليل القيمة الذاتية المعمم لـ Laplacian للرسم البياني. عادةً ما يعني هذا العمل مباشرةً مع مصفوفة Laplacian. إذا كانت مصفوفة البيانات الأصلية \(A\) لها شكل \(m \times n\)، فإن مصفوفة Laplacian للرسم البياني الثنائي المقابل لها شكل \((m + n) \times (m + n)\). ومع ذلك، في هذه الحالة، من الممكن العمل مباشرةً مع \(A\)، وهو أصغر وأكثر كفاءة.

يتم معالجة مصفوفة الإدخال \(A\) مسبقًا على النحو التالي:

\[A_n = R^{-1/2} A C^{-1/2}\]

حيث \(R\) هي المصفوفة القطرية مع الإدخال \(i\) يساوي \(\sum_{j} A_{ij}\) و \(C\) هي المصفوفة القطرية مع الإدخال \(j\) يساوي \(\sum_{i} A_{ij}\).

يوفر تحليل القيمة المفردة، \(A_n = U \Sigma V^\top\)، أقسام صفوف وأعمدة \(A\). تعطي مجموعة فرعية من المتجهات المفردة اليسرى أقسام الصف، وتعطي مجموعة فرعية من المتجهات المفردة اليمنى أقسام العمود.

\(\ell = \lceil \log_2 k \rceil\) المتجهات المفردة، بدءًا من الثانية، توفر معلومات التقسيم المطلوبة. يتم استخدامها لتشكيل المصفوفة \(Z\):

\[\begin{split}Z = \begin{bmatrix} R^{-1/2} U \\\\ C^{-1/2} V \end{bmatrix}\end{split}\]

حيث أعمدة \(U\) هي \(u_2, \dots, u_{\ell + 1}\)، وبالمثل لـ \(V\).

ثم يتم تجميع صفوف \(Z\) باستخدام k-means. توفر التسميات n_rows الأولى تقسيم الصف، وتوفر التسميات n_columns المتبقية تقسيم العمود.

أمثلة

  • sphx_glr_auto_examples_bicluster/plot_spectral_coclustering.py: مثال بسيط يوضح كيفية إنشاء مصفوفة بيانات مع مجموعات ثنائية وتطبيق هذه الطريقة عليها.

  • sphx_glr_auto_examples_bicluster/plot_bicluster_newsgroups.py: مثال على إيجاد مجموعات ثنائية في مجموعة بيانات مجموعات الأخبار العشرين.

المراجع

2.4.2. التجميع الثنائي الطيفي#

تفترض خوارزمية SpectralBiclustering أن مصفوفة بيانات الإدخال لها بنية رقعة شطرنج مخفية. قد يتم تقسيم صفوف وأعمدة المصفوفة ذات هذا الهيكل بحيث تكون إدخالات أي مجموعة ثنائية في حاصل الضرب الديكارتي لمجموعات الصفوف ومجموعات الأعمدة ثابتة تقريبًا. على سبيل المثال، إذا كان هناك قسمان للصفوف وثلاثة أقسام للأعمدة، فسينتمي كل صف إلى ثلاث مجموعات ثنائية، وسينتمي كل عمود إلى مجموعتين ثنائيتين.

تقوم الخوارزمية بتقسيم صفوف وأعمدة المصفوفة بحيث توفر مصفوفة رقعة الشطرنج الثابتة الكتلية المقابلة تقريبًا جيدًا للمصفوفة الأصلية.

الصيغة الرياضية

يتم أولاً تطبيع مصفوفة الإدخال \(A\) لجعل نمط رقعة الشطرنج أكثر وضوحًا. هناك ثلاث طرق ممكنة:

  1. تطبيع الصفوف والأعمدة المستقلة، كما هو الحال في التجميع المشترك الطيفي. تجعل هذه الطريقة مجموع الصفوف ثابتًا ومجموع الأعمدة ثابتًا مختلفًا.

  2. Bistochastization: تطبيع الصفوف والأعمدة المتكرر حتى التقارب. تجعل هذه الطريقة كل من الصفوف والأعمدة مجموعًا إلى نفس الثابت.

  3. تطبيع السجل: يتم حساب سجل مصفوفة البيانات: \(L = \log A\). ثم متوسط العمود \(\overline{L_{i \cdot}}\)، متوسط الصف \(\overline{L_{\cdot j}}\)، والمتوسط الإجمالي \(\overline{L_{\cdot \cdot}}\) من \(L\) يتم حسابها. يتم حساب المصفوفة النهائية وفقًا للصيغة

\[K_{ij} = L_{ij} - \overline{L_{i \cdot}} - \overline{L_{\cdot j}} + \overline{L_{\cdot \cdot}}\]

بعد التطبيع، يتم حساب المتجهات المفردة القليلة الأولى، تمامًا كما هو الحال في خوارزمية التجميع المشترك الطيفي.

إذا تم استخدام تطبيع السجل، فإن جميع المتجهات المفردة ذات مغزى. ومع ذلك، إذا تم استخدام التطبيع المستقل أو bistochastization، فإن المتجهات المفردة الأولى، \(u_1\) و \(v_1\). يتم تجاهلها. من الآن فصاعدًا، تشير المتجهات المفردة "الأولى" إلى \(u_2 \dots u_{p+1}\) و \(v_2 \dots v_{p+1}\) باستثناء حالة تطبيع السجل.

بالنظر إلى هذه المتجهات المفردة، يتم تصنيفها وفقًا لأيها يمكن تقريبه بشكل أفضل بواسطة متجه ثابت متقطع. تم العثور على التقريبات لكل متجه باستخدام k-means أحادي البعد وتم تسجيلها باستخدام المسافة الإقليدية. يتم اختيار مجموعة فرعية من أفضل متجه مفرد يسار ويمين. بعد ذلك، يتم عرض البيانات على هذه المجموعة الفرعية الأفضل من المتجهات المفردة وتجميعها.

على سبيل المثال، إذا تم حساب \(p\) متجهات مفردة، فسيتم العثور على \(q\) الأفضل كما هو موضح، حيث \(q<p\). دع \(U\) تكون المصفوفة ذات الأعمدة \(q\) أفضل المتجهات المفردة اليسرى، وبالمثل \(V\) لليمين. لتقسيم الصفوف، يتم عرض صفوف \(A\) على مساحة \(q\) الأبعاد: \(A * V\). معاملة \(m\) صفوف هذه المصفوفة \(m \times q\) كعينات والتجميع باستخدام k-means ينتج عنها تسميات الصفوف. وبالمثل، فإن إسقاط الأعمدة على \(A^{\top} * U\) وتجميع هذه المصفوفة \(n \times q\) ينتج عنه تسميات الأعمدة.

أمثلة

  • sphx_glr_auto_examples_bicluster/plot_spectral_biclustering.py: مثال بسيط يوضح كيفية إنشاء مصفوفة رقعة الشطرنج وتجميعها ثنائيًا.

المراجع

2.4.3. تقييم التجميع الثنائي#

هناك طريقتان لتقييم نتيجة التجميع الثنائي: داخلي وخارجي. تعتمد المقاييس الداخلية، مثل استقرار الكتلة، فقط على البيانات والنتيجة نفسها. لا توجد حاليًا مقاييس تجميع ثنائي داخلي في scikit-learn. تشير المقاييس الخارجية إلى مصدر خارجي للمعلومات، مثل الحل الحقيقي. عند العمل مع بيانات حقيقية، يكون الحل الحقيقي غير معروف عادةً، ولكن قد يكون التجميع الثنائي للبيانات الاصطناعية مفيدًا لتقييم الخوارزميات على وجه التحديد لأن الحل الحقيقي معروف.

لمقارنة مجموعة من التجميعات الثنائية التي تم العثور عليها بمجموعة التجميعات الثنائية الحقيقية، يلزم وجود مقياسين للتشابه: مقياس تشابه للتجميعات الثنائية الفردية، وطريقة لدمج أوجه التشابه الفردية هذه في درجة إجمالية.

لمقارنة التجميعات الثنائية الفردية، تم استخدام عدة مقاييس. في الوقت الحالي، تم تنفيذ فهرس Jaccard فقط:

\[J(A, B) = \frac{|A \cap B|}{|A| + |B| - |A \cap B|}\]

حيث \(A\) و \(B\) عبارة عن مجموعات ثنائية، \(|A \cap B|\) هو عدد العناصر في تقاطعها. يصل فهرس Jaccard إلى الحد الأدنى له وهو 0 عندما لا تتداخل التجميعات الثنائية على الإطلاق ويصل إلى الحد الأقصى له وهو 1 عندما تكون متطابقة.

تم تطوير عدة طرق لمقارنة مجموعتين من التجميعات الثنائية. في الوقت الحالي، تتوفر consensus_score (Hochreiter et. al.، 2010) فقط:

  1. احسب أوجه تشابه التجميع الثنائي لأزواج التجميعات الثنائية، واحدة في كل مجموعة، باستخدام فهرس Jaccard أو مقياس مشابه.

  2. قم بتعيين التجميعات الثنائية من مجموعة إلى أخرى بطريقة فردية لزيادة مجموع أوجه التشابه بينها. يتم تنفيذ هذه الخطوة باستخدام scipy.optimize.linear_sum_assignment، الذي يستخدم خوارزمية Jonker-Volgenant المعدلة.

  3. يتم قسمة مجموع أوجه التشابه النهائي على حجم المجموعة الأكبر.

تحدث درجة الإجماع الدنيا، 0، عندما تكون جميع أزواج التجميعات الثنائية متباينة تمامًا. تحدث الدرجة القصوى، 1، عندما تكون كلتا المجموعتين متطابقتين.

المراجع