1.1. النماذج الخطية#

فيما يلي مجموعة من الأساليب المُخصصة للانحدار حيث من المُتوقع أن تكون القيمة المستهدفة عبارة عن تركيبة خطية من الميزات. في الصيغة الرياضية، إذا كانت \(\hat{y}\) هي القيمة المُتوقعة.

\[\hat{y}(w, x) = w_0 + w_1 x_1 + ... + w_p x_p\]

عبر الوحدة، نُشير إلى المتجه \(w = (w_1, ..., w_p)\) كـ coef_ و \(w_0\) كـ intercept_.

لإجراء التصنيف باستخدام النماذج الخطية المُعممة، انظر الانحدار اللوجستي.

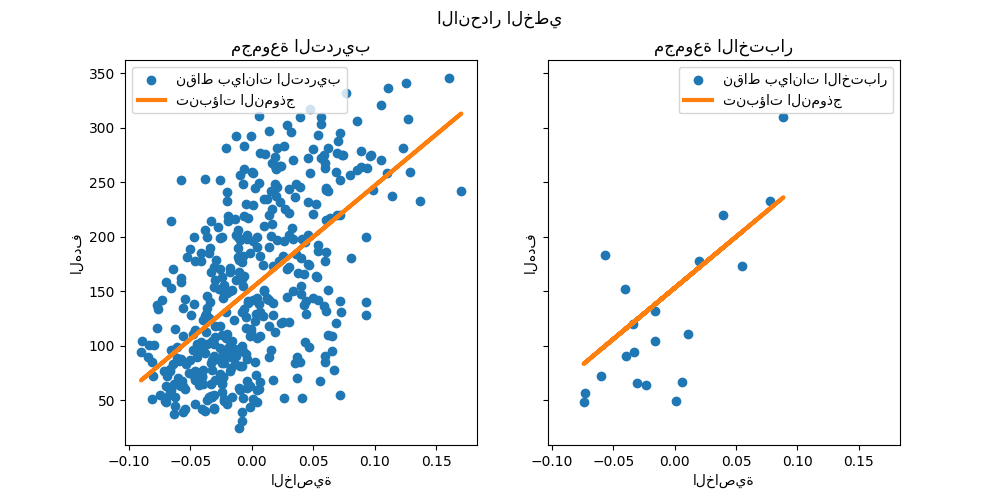
1.1.1. المربعات الصغرى العادية#

LinearRegression يُناسب نموذجًا خطيًا بمعاملات \(w = (w_1, ..., w_p)\) لتقليل مجموع البواقي من المربعات بين الأهداف المُلاحظة في مجموعة البيانات، و الأهداف التي تنبأ بها التقريب الخطي. رياضيًا، يحل مشكلة بالشكل:

\[\min_{w} || X w - y||_2^2\]
../_images/sphx_glr_plot_ols_001.png

سيأخذ LinearRegression في أسلوبه fit مصفوفات X و y ويُخزن المعاملات \(w\) للنموذج الخطي في عضويته coef_:

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
>>> reg.coef_
array([0.5, 0.5])

تعتمد تقديرات المعاملات للمربعات الصغرى العادية على استقلال الميزات. عندما تكون الميزات مُرتبطة و أعمدة مصفوفة التصميم \(X\) لها تبعية خطية تقريبية، تصبح مصفوفة التصميم قريبة من المفردة ونتيجة لذلك، يصبح تقدير المربعات الصغرى حساسًا للغاية للأخطاء العشوائية في الهدف المُلاحظ، مما يُنتج تباينًا كبيرًا. يمكن أن تنشأ حالة التعدد الخطي هذه، على سبيل المثال، عندما يتم جمع البيانات بدون تصميم تجريبي.

أمثلة

1.1.1.1. المربعات الصغرى غير السالبة#

من الممكن تقييد جميع المعاملات لتكون غير سالبة، وهو ما قد يكون مفيدًا عندما تُمثِّل بعض الكميات المادية أو غير السالبة بشكل طبيعي (على سبيل المثال، عدد الترددات أو أسعار السلع). LinearRegression يقبل معلمة منطقية positive: عند تعيينها إلى True، يتم تطبيق المربعات الصغرى غير السالبة.

أمثلة

1.1.1.2. تعقيد المربعات الصغرى العادية#

يتم حساب حل المربعات الصغرى باستخدام تحليل القيمة المنفردة لـ X. إذا كانت X مصفوفة ذات شكل (n_samples, n_features)، فإن هذه الطريقة لها تكلفة \(O(n_{\text{samples}} n_{\text{features}}^2)\)، بافتراض أن \(n_{\text{samples}} \geq n_{\text{features}}\).

1.1.2. انحدار ريدج والتصنيف#

1.1.2.1. الانحدار#

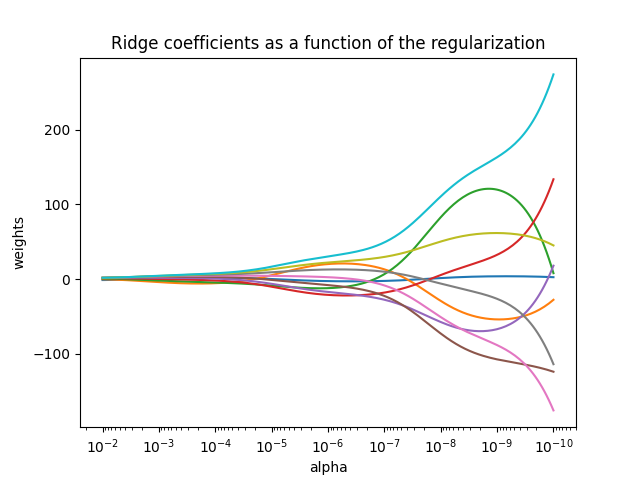
يعالج انحدار Ridge بعض مشاكل المربعات الصغرى العادية عن طريق فرض عقوبة على حجم المعاملات. تُقلل معاملات ريدج مجموع البواقي المُعاقب من المربعات:

\[\min_{w} || X w - y||_2^2 + \alpha ||w||_2^2\]

تتحكم معلمة التعقيد \(\alpha \geq 0\) في مقدار الانكماش: كلما زادت قيمة \(\alpha\)، زاد مقدار الانكماش وبالتالي أصبحت المعاملات أكثر قوة للتعددية الخطية.

../_images/sphx_glr_plot_ridge_path_001.png

كما هو الحال مع النماذج الخطية الأخرى، سيأخذ Ridge في أسلوبه fit مصفوفات X و y ويُخزن المعاملات \(w\) للنموذج الخطي في عضويته coef_:

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge(alpha=.5)
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5)
>>> reg.coef_
array([0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...

لاحظ أن الفئة Ridge تسمح للمستخدم بتحديد أنه يجب اختيار المحلل تلقائيًا عن طريق تعيين solver="auto". عند تحديد هذا الخيار، سيختار Ridge بين محللات "lbfgs" و "cholesky" و "sparse_cg". سيبدأ Ridge في فحص الشروط الموضحة في الجدول التالي من أعلى إلى أسفل. إذا كان الشرط صحيحًا، فسيتم اختيار المحلل المُقابل.

1.1.2.2. التصنيف#

يحتوي مُنحدِر Ridge على مُتغير مُصنف: RidgeClassifier. يُحوِّل هذا المُصنف أولاً الأهداف الثنائية إلى {-1, 1} ثم يُعامل المشكلة كمهمة انحدار، ويُحسِّن نفس الهدف على النحو الوارد أعلاه. تُقابل الفئة المُتوقعة إشارة تنبؤ المُنحدِر. بالنسبة للتصنيف متعدد الفئات، يتم مُعالجة المشكلة على أنها انحدار متعدد المخرجات، وتُقابل الفئة المُتوقعة الإخراج ذي القيمة الأعلى.

قد يبدو من المشكوك فيه استخدام خسارة المربعات الصغرى (المُعاقبة) لملاءمة نموذج تصنيف بدلاً من خسائر اللوجستية أو المفصلية الأكثر تقليدية. ومع ذلك، من الناحية العملية، يمكن أن تؤدي جميع هذه النماذج إلى درجات تحقق متبادل مُتشابهة من حيث الدقة أو الدقة / الاستدعاء، بينما خسارة المربعات الصغرى المُعاقبة التي يستخدمها RidgeClassifier تسمح باختيار مُختلف تمامًا للمحللات العددية مع ملفات تعريف أداء حسابية مُتميزة.

يمكن أن يكون RidgeClassifier أسرع بكثير من على سبيل المثال LogisticRegression مع عدد كبير من الفئات لأنه يمكنه حساب مصفوفة الإسقاط \((X^T X)^{-1} X^T\) مرة واحدة فقط.

يُشار أحيانًا إلى هذا المُصنف باسم آلات متجه دعم المربعات الصغرى مع نواة خطية.

أمثلة

1.1.2.3. تعقيد ريدج#

هذه الطريقة لها نفس ترتيب التعقيد مثل المربعات الصغرى العادية.

1.1.2.4. تعيين معلمة التنظيم: التحقق المتبادل لترك واحد#

RidgeCV و RidgeClassifierCV يُطبقان انحدار / تصنيف ريدج مع التحقق المتبادل المُدمج لمعلمة alpha. يعملان بنفس طريقة GridSearchCV باستثناء أنه يتم تعيينه افتراضيًا إلى التحقق المتبادل الفعال لترك واحد. عند استخدام التحقق المتبادل الافتراضي، لا يمكن أن تكون alpha 0 بسبب الصيغة المُستخدمة لحساب خطأ ترك واحد. انظر [RL2007] للتفاصيل.

مثال على الاستخدام:

>>> import numpy as np
>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13))
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
RidgeCV(alphas=array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
      1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06]))
>>> reg.alpha_
0.01

سيؤدي تحديد قيمة سمة cv إلى تشغيل استخدام التحقق المتبادل باستخدام GridSearchCV، على سبيل المثال cv=10 للتحقق المتبادل من 10 طيات، بدلاً من التحقق المتبادل لترك واحد.

المراجع#
[RL2007]

"ملاحظات حول المربعات الصغرى المُنظّمة", Rifkin & Lippert (التقرير الفني <http://cbcl.mit.edu/publications/ps/MIT-CSAIL-TR-2007-025.pdf>`_، شرائح الدورة).

1.1.3. Lasso#

Lasso هو نموذج خطي يُقدِّر معاملات متفرقة. إنه مفيد في بعض السياقات نظرًا لميله إلى تفضيل الحلول التي تحتوي على عدد أقل من المعاملات غير الصفرية، مما يُقلل بشكل فعال من عدد الميزات التي يعتمد عليها الحل المُعين. لهذا السبب، يُعد Lasso ومتغيراته أساسيين في مجال الاستشعار المضغوط. في ظل ظروف مُعينة، يمكنه استرداد مجموعة المعاملات غير الصفرية الدقيقة (انظر sphx_glr_auto_examples_applications_plot_tomography_l1_reconstruction.py).

رياضيًا، يتكون من نموذج خطي مع مُصطلح تنظيم مُضاف. دالة الهدف التي يجب تقليلها هي:

\[\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha ||w||_1}\]

وبالتالي، يحل تقدير lasso تقليل عقوبة المربعات الصغرى مع إضافة \(\alpha ||w||_1\)، حيث \(\alpha\) ثابت و \(||w||_1\) هي قاعدة \(\ell_1\) لـ متجه المعاملات.

يستخدم التطبيق في الفئة Lasso النزول الإحداثي كـ خوارزمية لملاءمة المعاملات. انظر انحدار الزاوية الصغرى للحصول على تطبيق آخر:

>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha=0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1)
>>> reg.predict([[1, 1]])
array([0.8])

تُعد دالة lasso_path مفيدة للمهام ذات المستوى الأدنى، حيث إنها تحسب المعاملات على طول المسار الكامل للقيم المُمكنة.

أمثلة

ملاحظة

اختيار الميزات باستخدام Lasso

نظرًا لأن انحدار Lasso يُعطي نماذج متفرقة، فإنه يمكن استخدامه لاختيار الميزات، كما هو مُفصَّل في اختيار الميزات القائم على L1.

المراجع#

يشرح المرجعان التاليان التكرارات المُستخدمة في محلل النزول الإحداثي لـ scikit-learn، وكذلك حساب فجوة الازدواجية المُستخدم للتحكم في التقارب.

  • "مسار التنظيم للنماذج الخطية المُعممة عن طريق النزول الإحداثي", Friedman, Hastie & Tibshirani, J Stat Softw, 2010 (الورقة).

  • "أسلوب نقطة داخلية للمربعات الصغرى المُنظّمة بـ L1 واسعة النطاق," S. J. Kim, K. Koh, M. Lustig, S. Boyd and D. Gorinevsky, في IEEE Journal of Selected Topics in Signal Processing، 2007 (الورقة)

1.1.3.1. تعيين معلمة التنظيم#

تتحكم معلمة alpha في درجة تفرق المعاملات المُقدّرة.

1.1.3.1.1. استخدام التحقق المتبادل#

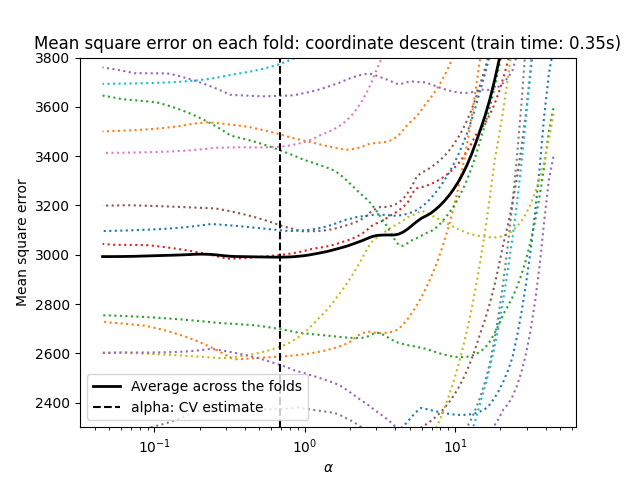
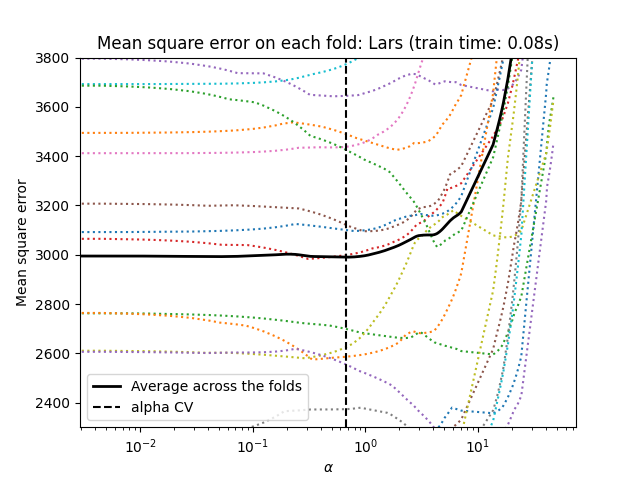
يُظهِر scikit-learn الكائنات التي تُعيِّن معلمة Lasso alpha عن طريق التحقق المتبادل: LassoCV و LassoLarsCV. LassoLarsCV يعتمد على خوارزمية انحدار الزاوية الصغرى الموضحة أدناه.

بالنسبة لمجموعات البيانات عالية الأبعاد ذات العديد من الميزات الخطية، LassoCV غالبًا ما يكون مُفضلًا. ومع ذلك، فإن LassoLarsCV له ميزة استكشاف المزيد من قيم معلمة alpha ذات الصلة، و إذا كان عدد العينات صغيرًا جدًا مُقارنةً بعدد الميزات، فإنه غالبًا ما يكون أسرع من LassoCV.

lasso_cv_1 lasso_cv_2

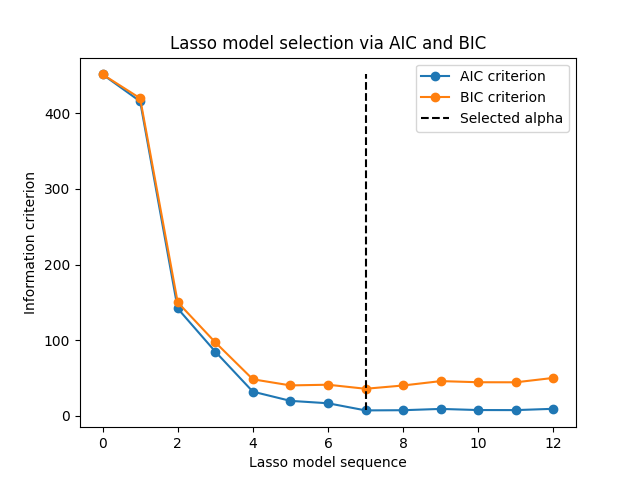
1.1.3.1.2. اختيار النموذج القائم على معيار المعلومات#

بدلاً من ذلك، يقترح المُقدِّر LassoLarsIC استخدام معيار معلومات Akaike (AIC) ومعيار معلومات Bayes (BIC). إنه بديل أقل تكلفة من الناحية الحسابية للعثور على القيمة المثلى لـ alpha حيث يتم حساب مسار التنظيم مرة واحدة فقط بدلاً من k + 1 مرة عند استخدام التحقق المتبادل k-fold.

في الواقع، يتم حساب هذه المعايير على مجموعة التدريب داخل العينة. باختصار، يعاقبون الدرجات المُتفائلة جدًا لنماذج Lasso المختلفة بواسطة مرونتها (راجع قسم "التفاصيل الرياضية" أدناه).

ومع ذلك، تحتاج هذه المعايير إلى تقدير مناسب لدرجات حرية الحل، ويتم اشتقاقها لعينات كبيرة (نتائج مقاربة) وتفترض أن النموذج الصحيح هو مرشح قيد التحقيق. كما أنها تميل إلى الانهيار عندما تكون المشكلة سيئة الشرط (على سبيل المثال، المزيد من الميزات من العينات).

../_images/sphx_glr_plot_lasso_lars_ic_001.png

أمثلة

1.1.3.1.3. معايير AIC و BIC#

قد يختلف تعريف AIC (وبالتالي BIC) في الأدبيات. في هذا القسم، نُقدم المزيد من المعلومات حول المعيار المحسوب في scikit-learn.

التفاصيل الرياضية#

يتم تعريف معيار AIC على النحو التالي:

\[AIC = -2 \log(\hat{L}) + 2 d\]

حيث \(\hat{L}\) هو أقصى احتمالية للنموذج و \(d\) هو عدد المعلمات (يُشار إليها أيضًا بدرجات الحرية في القسم السابق).

يستبدل تعريف BIC الثابت \(2\) بـ \(\log(N)\):

\[BIC = -2 \log(\hat{L}) + \log(N) d\]

حيث \(N\) هو عدد العينات.

بالنسبة لنموذج غاوسي خطي، يتم تعريف أقصى احتمالية للسجل على النحو التالي:

\[\log(\hat{L}) = - \frac{n}{2} \log(2 \pi) - \frac{n}{2} \ln(\sigma^2) - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{2\sigma^2}\]

حيث \(\sigma^2\) هو تقدير لتباين الضوضاء، \(y_i\) و \(\hat{y}_i\) هما الأهداف الحقيقية والمتوقعة على التوالي، و \(n\) هو عدد العينات.

يؤدي توصيل أقصى احتمالية للسجل في صيغة AIC إلى:

\[AIC = n \log(2 \pi \sigma^2) + \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sigma^2} + 2 d\]

يتم تجاهل المصطلح الأول من التعبير أعلاه أحيانًا لأنه ثابت عندما يتم توفير \(\sigma^2\). بالإضافة إلى ذلك، يُذكر أحيانًا أن AIC يُعادل إحصائية \(C_p\) [12]. ومع ذلك، بمعنى دقيق، فإنه يُعادل فقط حتى ثابت مُعين وعامل ضربي.

أخيرًا، ذكرنا أعلاه أن \(\sigma^2\) هو تقدير لـ تباين الضوضاء. في LassoLarsIC عندما لا يتم توفير معلمة noise_variance (افتراضي)، يتم تقدير تباين الضوضاء عبر المُقدِّر غير المُتحيز [13] المُعرَّف على النحو التالي:

\[\sigma^2 = \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{n - p}\]

حيث \(p\) هو عدد الميزات و \(\hat{y}_i\) هو الهدف المتوقع باستخدام انحدار المربعات الصغرى العادية. لاحظ أن هذه الصيغة صالحة فقط عندما n_samples > n_features.

المراجع

1.1.3.1.4. مقارنة مع معلمة التنظيم لـ SVM#

التكافؤ بين alpha ومعلمة التنظيم لـ SVM، C مُعطى بواسطة alpha = 1 / C أو alpha = 1 / (n_samples * C)، اعتمادًا على المُقدِّر ودالة الهدف الدقيقة التي يُحسِّنها النموذج.

1.1.4. Lasso متعدد المهام#

MultiTaskLasso هو نموذج خطي يُقدِّر المعاملات المتفرقة لمشاكل الانحدار المتعددة بشكل مُشترك: y هي مصفوفة ثنائية الأبعاد، ذات شكل (n_samples, n_tasks). القيد هو أن الميزات المحددة هي نفسها لجميع مشاكل الانحدار، وتسمى أيضًا المهام.

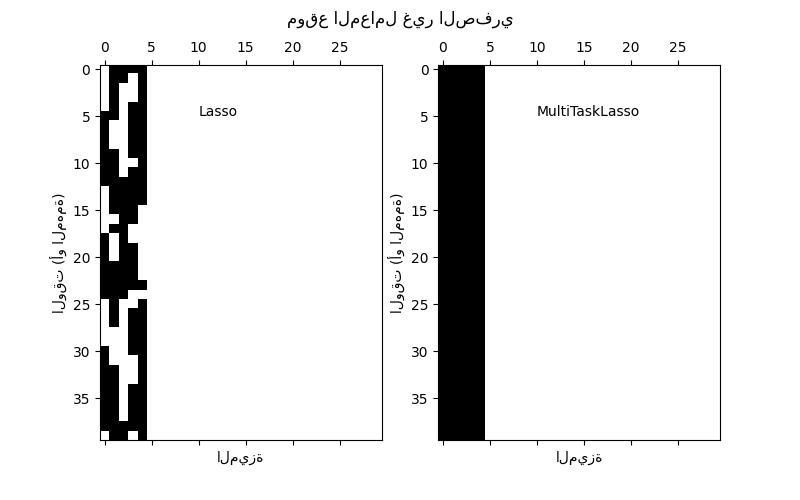
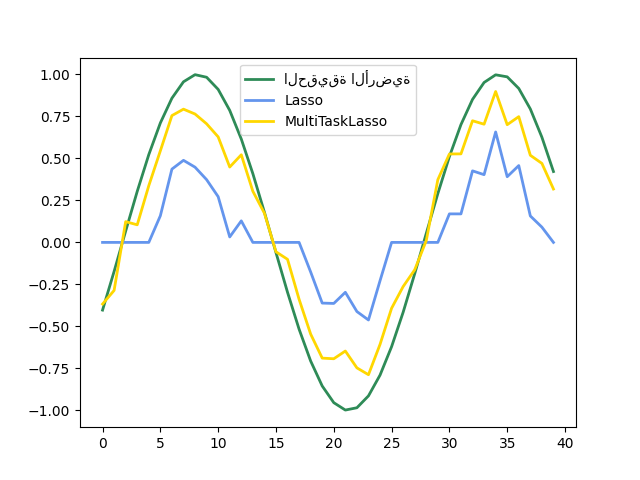
تُقارن الصورة التالية موقع الإدخالات غير الصفرية في مصفوفة المعاملات W التي تم الحصول عليها باستخدام Lasso بسيط أو MultiTaskLasso. تُعطي تقديرات Lasso قيمًا غير صفرية مُشتتة بينما القيم غير الصفرية لـ MultiTaskLasso هي أعمدة كاملة.

multi_task_lasso_1 multi_task_lasso_2

ملاءمة نموذج سلسلة زمنية، بفرض أن تكون أي ميزة نشطة نشطة في جميع الأوقات.

أمثلة

التفاصيل الرياضية#

رياضيًا، يتكون من نموذج خطي مُدرَّب بمزيج من قاعدة \(\ell_1\) \(\ell_2\) لتنظيم. دالة الهدف التي يجب تقليلها هي:

\[\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W - Y||_{\text{Fro}} ^ 2 + \alpha ||W||_{21}}\]

حيث يُشير \(\text{Fro}\) إلى قاعدة Frobenius

\[||A||_{\text{Fro}} = \sqrt{\sum_{ij} a_{ij}^2}\]

و \(\ell_1\) \(\ell_2\) تقرأ

\[||A||_{2 1} = \sum_i \sqrt{\sum_j a_{ij}^2}.\]

يستخدم التطبيق في الفئة MultiTaskLasso النزول الإحداثي كخوارزمية لملاءمة المعاملات.

1.1.5. Elastic-Net#

ElasticNet هو نموذج انحدار خطي مُدرَّب بكل من تنظيم \(\ell_1\) و \(\ell_2\) للمعاملات. يسمح هذا المزيج بتعلم نموذج متفرق حيث يكون عدد قليل من الأوزان غير صفري مثل Lasso، مع الحفاظ على خصائص التنظيم لـ Ridge. نتحكم في التركيبة المُحدبة لـ \(\ell_1\) و \(\ell_2\) باستخدام معلمة l1_ratio.

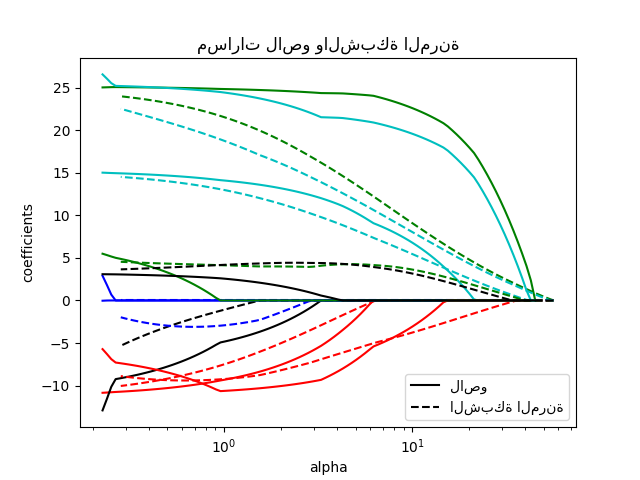
Elastic-net مفيد عندما يكون هناك العديد من الميزات المُرتبطة ببعضها البعض. من المرجح أن يختار Lasso واحدًا من هذه بشكل عشوائي، بينما من المرجح أن يختار Elastic-Net كليهما.

ميزة عملية للمُفاضلة بين Lasso و Ridge هي أنه يسمح لـ Elastic-Net بوراثة بعض استقرار Ridge تحت الدوران.

دالة الهدف التي يجب تقليلها هي في هذه الحالة

\[\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha \rho ||w||_1 + \frac{\alpha(1-\rho)}{2} ||w||_2 ^ 2}\]
../_images/sphx_glr_plot_lasso_lasso_lars_elasticnet_path_002.png

يمكن استخدام الفئة ElasticNetCV لضبط المعلمات alpha (\(\alpha\)) و l1_ratio (\(\rho\)) عن طريق التحقق المتبادل.

أمثلة

المراجع#

يشرح المرجعان التاليان التكرارات المُستخدمة في محلل النزول الإحداثي لـ scikit-learn، وكذلك حساب فجوة الازدواجية المُستخدم للتحكم في التقارب.

  • "مسار التنظيم للنماذج الخطية المُعممة عن طريق النزول الإحداثي", Friedman, Hastie & Tibshirani, J Stat Softw, 2010 (الورقة).

  • "أسلوب نقطة داخلية للمربعات الصغرى المُنظّمة بـ L1 واسعة النطاق," S. J. Kim, K. Koh, M. Lustig, S. Boyd and D. Gorinevsky, في IEEE Journal of Selected Topics in Signal Processing، 2007 (الورقة)

1.1.6. Elastic-Net متعدد المهام#

MultiTaskElasticNet هو نموذج شبكة مرنة يُقدِّر المعاملات المتفرقة لمشاكل الانحدار المتعددة بشكل مُشترك: Y هي مصفوفة ثنائية الأبعاد ذات شكل (n_samples, n_tasks). القيد هو أن الميزات المحددة هي نفسها لجميع مشاكل الانحدار، وتسمى أيضًا المهام.

رياضيًا، يتكون من نموذج خطي مُدرَّب بمزيج من قاعدة \(\ell_1\) \(\ell_2\) وقاعدة \(\ell_2\) للتنظيم. دالة الهدف التي يجب تقليلها هي:

\[\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W - Y||_{\text{Fro}}^2 + \alpha \rho ||W||_{2 1} + \frac{\alpha(1-\rho)}{2} ||W||_{\text{Fro}}^2}\]

يستخدم التطبيق في الفئة MultiTaskElasticNet النزول الإحداثي كـ خوارزمية لملاءمة المعاملات.

يمكن استخدام الفئة MultiTaskElasticNetCV لضبط المعلمات alpha (\(\alpha\)) و l1_ratio (\(\rho\)) عن طريق التحقق المتبادل.

1.1.7. انحدار الزاوية الصغرى#

انحدار الزاوية الصغرى (LARS) هو خوارزمية انحدار لـ البيانات عالية الأبعاد، طورتها برادلي إيفرون، تريفور هاستي، إيان جونستون وروبرت تيبيشيراني. LARS مُشابه لانحدار الخطوة الأمامية. في كل خطوة، يجد الميزة الأكثر ارتباطًا بـ الهدف. عندما يكون هناك العديد من الميزات ذات الارتباط المتساوي، بدلاً من الاستمرار على طول نفس الميزة، فإنه يتقدم في اتجاه متساوي الزوايا بين الميزات.

مزايا LARS هي:

  • إنه فعال عدديًا في السياقات التي يكون فيها عدد الميزات أكبر بكثير من عدد العينات.

  • إنه سريع حسابيًا مثل الاختيار الأمامي وله نفس ترتيب التعقيد مثل المربعات الصغرى العادية.

  • إنه يُنتج مسار حل خطي مُتكسر كامل، وهو مفيد في التحقق المتبادل أو المحاولات المُشابهة لضبط النموذج.

  • إذا كانت ميزتان مُرتبطتين تقريبًا بنفس القدر بالهدف، فإن معاملاتهما يجب أن تزداد بنفس المعدل تقريبًا. وبالتالي تتصرف الخوارزمية كما يتوقع الحدس، و هي أيضًا أكثر استقرارًا.

  • من السهل تعديله لإنتاج حلول لمُقدِّرات أخرى، مثل Lasso.

تشمل عيوب أسلوب LARS ما يلي:

  • لأن LARS يعتمد على إعادة ملاءمة متكررة لـ البواقي، سيبدو حساسًا بشكل خاص لـ آثار الضوضاء. تمت مناقشة هذه المشكلة بالتفصيل بواسطة Weisberg في قسم المناقشة من مقالة Efron وآخرون (2004) Annals of Statistics.

يمكن استخدام نموذج LARS عبر المُقدِّر Lars، أو تطبيقه منخفض المستوى lars_path أو lars_path_gram.

1.1.8. LARS Lasso#

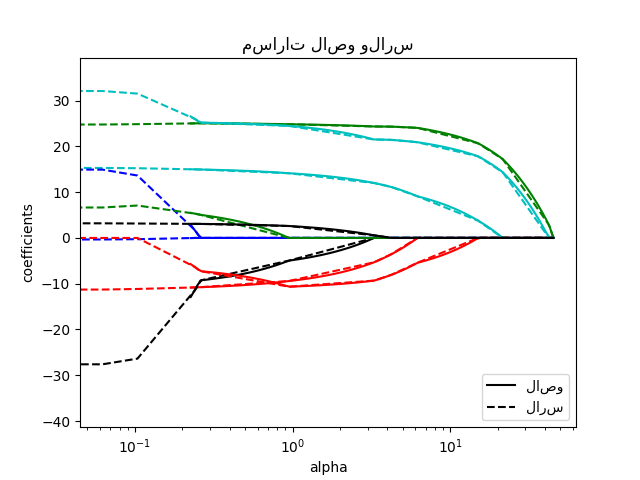
LassoLars هو نموذج lasso مُطبق باستخدام خوارزمية LARS، وعلى عكس التطبيق القائم على النزول الإحداثي، يُعطي هذا الحل الدقيق، وهو خطي متعدد التعريف كـ دالة لقاعدة معاملاته.

../_images/sphx_glr_plot_lasso_lasso_lars_elasticnet_path_001.png 
>>> from sklearn import linear_model
>>> reg = linear_model.LassoLars(alpha=.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
LassoLars(alpha=0.1)
>>> reg.coef_
array([0.6..., 0.        ])

أمثلة

تُوفر خوارزمية Lars المسار الكامل للمعاملات على طول معلمة التنظيم مجانًا تقريبًا، وبالتالي فإن العملية الشائعة هي استرداد المسار باستخدام إحدى الدالتين lars_path أو lars_path_gram.

الصيغة الرياضية#

الخوارزمية مُشابهة لانحدار الخطوة الأمامية، ولكن بدلاً من تضمين الميزات في كل خطوة، يتم زيادة المعاملات المُقدَّرة في اتجاه متساوي الزوايا لكل ارتباط واحد مع الباقي.

بدلاً من إعطاء نتيجة متجه، يتكون حل LARS من منحنى يُشير إلى الحل لكل قيمة لقاعدة \(\ell_1\) لـ متجه المعلمة. يتم تخزين مسار المعاملات الكامل في المصفوفة coef_path_ ذات الشكل (n_features, max_features + 1). العمود الأول دائمًا صفر.

المراجع

1.1.9. مطاردة التطابق المتعامد (OMP)#

OrthogonalMatchingPursuit و orthogonal_mp يُطبقان خوارزمية OMP لتقريب ملاءمة نموذج خطي مع قيود مفروضة على عدد المعاملات غير الصفرية (أي قاعدة \(\ell_0\) الزائفة).

نظرًا لكونه أسلوب اختيار ميزات أمامي مثل انحدار الزاوية الصغرى، يمكن لمطاردة التطابق المتعامد تقريب متجه الحل الأمثل بعدد ثابت من العناصر غير الصفرية:

\[\underset{w}{\operatorname{arg\,min\,}} ||y - Xw||_2^2 \text{ subject to } ||w||_0 \leq n_{\text{nonzero_coefs}}\]

بدلاً من ذلك، يمكن لمطاردة التطابق المتعامد استهداف خطأ مُحدد بدلاً من عدد مُحدد من المعاملات غير الصفرية. يمكن التعبير عن هذا كـ:

\[\underset{w}{\operatorname{arg\,min\,}} ||w||_0 \text{ subject to } ||y-Xw||_2^2 \leq \text{tol}\]

يعتمد OMP على خوارزمية جشعة تتضمن في كل خطوة الذرة الأكثر ارتباطًا بالباقي الحالي. إنه مُشابه لأسلوب مطاردة التطابق (MP) الأبسط، ولكنه أفضل من حيث أنه في كل تكرار، يتم إعادة حساب الباقي باستخدام إسقاط متعامد على فضاء عناصر القاموس المختارة سابقًا.

أمثلة

المراجع#

1.1.10. الانحدار البايزي#

يمكن استخدام تقنيات الانحدار البايزي لتضمين معلمات التنظيم في إجراء التقدير: لا يتم تعيين معلمة التنظيم بمعنى صارم ولكن يتم ضبطها على البيانات الموجودة.

يمكن القيام بذلك عن طريق إدخال مُسبقات غير إعلامية على المعلمات الفائقة للنموذج. تنظيم \(\ell_{2}\) المُستخدم في انحدار ريدج والتصنيف يُعادل إيجاد أقصى تقدير لاحق في ظل مُسبق غاوسي على المعاملات \(w\) بدقة \(\lambda^{-1}\). بدلاً من تعيين lambda يدويًا، من الممكن مُعالجتها كمتغير عشوائي يتم تقديره من البيانات.

للحصول على نموذج احتمالي بالكامل، يُفترض أن يكون الإخراج \(y\) موزعًا غاوسيًا حول \(X w\):

\[p(y|X,w,\alpha) = \mathcal{N}(y|X w,\alpha^{-1})\]

حيث يتم مُعالجة \(\alpha\) مرة أخرى كمتغير عشوائي يتم تقديره من البيانات.

مزايا الانحدار البايزي هي:

  • يتكيف مع البيانات الموجودة.

  • يمكن استخدامه لتضمين معلمات التنظيم في إجراء التقدير.

تشمل عيوب الانحدار البايزي ما يلي:

  • يمكن أن يكون استدلال النموذج مُستهلكًا للوقت.

المراجع#

  • تم تقديم مقدمة جيدة للأساليب البايزية في C. Bishop: Pattern Recognition and Machine learning

  • تم تفصيل الخوارزمية الأصلية في كتاب التعلم البايزي للشبكات العصبية بواسطة Radford M. Neal

1.1.10.1. انحدار ريدج البايزي#

BayesianRidge يُقدِّر نموذجًا احتماليًا لـ مشكلة الانحدار كما هو موضح أعلاه. المُسبق للمعامل \(w\) مُعطى بواسطة توزيع غاوسي كروي:

\[p(w|\lambda) = \mathcal{N}(w|0,\lambda^{-1}\mathbf{I}_{p})\]

يتم اختيار المُسبقات على \(\alpha\) و \(\lambda\) لتكون توزيعات جاما، المُسبق المُقترن لدقة التوزيع الغاوسي. يُسمى النموذج الناتج انحدار ريدج البايزي، وهو مُشابه لـ Ridge الكلاسيكي.

يتم تقدير المعلمات \(w\) و \(\alpha\) و \(\lambda\) بشكل مُشترك أثناء ملاءمة النموذج، مع تقدير معلمات التنظيم \(\alpha\) و \(\lambda\) عن طريق تعظيم احتمالية السجل الهامشي. يعتمد تطبيق scikit-learn على الخوارزمية الموضحة في الملحق أ من (Tipping، 2001) حيث يتم تحديث المعلمات \(\alpha\) و \(\lambda\) كما هو مُقترح في (MacKay، 1992). يمكن تعيين القيمة الأولية لإجراء التعظيم باستخدام المعلمات الفائقة alpha_init و lambda_init.

هناك أربع معلمات فائقة أخرى، \(\alpha_1\) و \(\alpha_2\) و \(\lambda_1\) و \(\lambda_2\) لتوزيعات جاما السابقة على \(\alpha\) و \(\lambda\). عادةً ما يتم اختيار هذه لتكون غير إعلامية. افتراضيًا \(\alpha_1 = \alpha_2 = \lambda_1 = \lambda_2 = 10^{-6}\).

يُستخدم انحدار ريدج البايزي للانحدار:

>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge()

بعد ملاءمته، يمكن استخدام النموذج للتنبؤ بقيم جديدة:

>>> reg.predict([[1, 0.]])
array([0.50000013])

يمكن الوصول إلى معاملات \(w\) للنموذج:

>>> reg.coef_
array([0.49999993, 0.49999993])

نظرًا لإطار العمل البايزي، فإن الأوزان التي تم العثور عليها تختلف قليلاً عن تلك التي تم العثور عليها بواسطة المربعات الصغرى العادية. ومع ذلك، فإن انحدار ريدج البايزي أكثر قوة للمشاكل سيئة الوضع.

أمثلة

  • sphx_glr_auto_examples_linear_model_plot_bayesian_ridge_curvefit.py

المراجع#

1.1.10.2. تحديد الصلة التلقائي - ARD#

تحديد الصلة التلقائي (كما هو مُطبق في ARDRegression) هو نوع من النماذج الخطية يُشبه جدًا انحدار ريدج البايزي، ولكنه يؤدي إلى معاملات \(w\) أكثر تفرقًا [1] [2].

ARDRegression يضع مُسبقًا مُختلفًا على \(w\): إنه يُسقط التوزيع الغاوسي الكروي لتوزيع غاوسي بيضاوي مُتمركز. هذا يعني أنه يمكن رسم كل معامل \(w_{i}\) من توزيع غاوسي، مُتمركز على الصفر وبدقة \(\lambda_{i}\):

\[p(w|\lambda) = \mathcal{N}(w|0,A^{-1})\]

مع كون \(A\) مصفوفة قطرية موجبة مُحددة و \(\text{diag}(A) = \lambda = \{\lambda_{1},...,\lambda_{p}\}\).

على عكس انحدار ريدج البايزي، كل إحداثي من \(w_{i}\) له انحرافه المعياري الخاص \(\frac{1}{\lambda_i}\). يتم اختيار المُسبق على جميع \(\lambda_i\) ليكون نفس توزيع جاما المُعطى بواسطة المعلمات الفائقة \(\lambda_1\) و \(\lambda_2\).

يُعرف ARD أيضًا في الأدبيات باسم التعلم البايزي المتفرق و آلة متجه الصلة [3] [4]. لمقارنة مُفصلة بين ARD و انحدار ريدج البايزي، انظر المثال أدناه.

أمثلة

المراجع

1.1.11. الانحدار اللوجستي#

يتم تطبيق الانحدار اللوجستي في LogisticRegression. على الرغم من اسمه، فإنه يتم تطبيقه كنموذج خطي للتصنيف بدلاً من الانحدار من حيث تسمية scikit-learn / ML. يُعرف الانحدار اللوجستي أيضًا في الأدبيات باسم انحدار logit، تصنيف الحد الأقصى للإنتروبيا (MaxEnt) أو المُصنف اللوغاريتمي الخطي. في هذا النموذج، يتم نمذجة الاحتمالات التي تصف النتائج المُمكنة لتجربة واحدة باستخدام دالة لوجستية.

يمكن لهذا التطبيق ملاءمة الانحدار اللوجستي الثنائي أو واحد مقابل البقية أو متعدد الحدود مع تنظيم \(\ell_1\) أو \(\ell_2\) أو Elastic-Net اختياري.

ملاحظة

التنظيم

يتم تطبيق التنظيم افتراضيًا، وهو أمر شائع في التعلم الآلي ولكن ليس في الإحصاء. ميزة أخرى للتنظيم هي أنه يُحسِّن الاستقرار العددي. لا يُعادل التنظيم تعيين C إلى قيمة عالية جدًا.

ملاحظة

الانحدار اللوجستي كحالة خاصة من النماذج الخطية المُعممة (GLM)

الانحدار اللوجستي هو حالة خاصة من النماذج الخطية المُعممة مع توزيع شرطي ذي حدين / برنولي وربط Logit. يمكن استخدام الناتج العددي للانحدار اللوجستي، وهو الاحتمال المُتوقع، كمُصنف عن طريق تطبيق عتبة (افتراضيًا 0.5) عليه. هذه هي الطريقة التي يتم تطبيقها في scikit-learn، لذلك يتوقع هدفًا فئويًا، مما يجعل الانحدار اللوجستي مُصنفًا.

أمثلة

1.1.11.1. الحالة الثنائية#

لتسهيل التدوين، نفترض أن الهدف \(y_i\) يأخذ قيمًا في المجموعة \(\{0, 1\}\) لنقطة البيانات \(i\). بمجرد ملاءمته، أسلوب predict_proba لـ LogisticRegression يتنبأ باحتمالية الفئة الإيجابية \(P(y_i=1|X_i)\) كـ

\[\hat{p}(X_i) = \operatorname{expit}(X_i w + w_0) = \frac{1}{1 + \exp(-X_i w - w_0)}.\]

كمشكلة تحسين، يُقلل الانحدار اللوجستي الثنائي مع مُصطلح التنظيم \(r(w)\) دالة التكلفة التالية:

(1)#\[\min_{w} \frac{1}{S}\sum_{i=1}^n s_i \left(-y_i \log(\hat{p}(X_i)) - (1 - y_i) \log(1 - \hat{p}(X_i))\right) + \frac{r(w)}{S C}\,,\]

حيث \({s_i}\) تُقابل الأوزان المُعيَّنة من قبل المستخدم لـ عينة تدريب مُحددة (يتم تشكيل المتجه \(s\) عن طريق ضرب أوزان الفئة وأوزان العينة حسب العنصر)، والمجموع \(S = \sum_{i=1}^n s_i\).

نُقدم حاليًا أربعة خيارات لمُصطلح التنظيم \(r(w)\) عبر وسيطة penalty:

penalty

\(r(w)\)

None

\(0\)

\(\ell_1\)

\(\|w\|_1\)

\(\ell_2\)

\(\frac{1}{2}\|w\|_2^2 = \frac{1}{2}w^T w\)

ElasticNet

\(\frac{1 - \rho}{2}w^T w + \rho \|w\|_1\)

بالنسبة لـ ElasticNet، \(\rho\) (التي تُقابل معلمة l1_ratio) تتحكم في قوة تنظيم \(\ell_1\) مقابل تنظيم \(\ell_2\). Elastic-Net يُعادل \(\ell_1\) عندما \(\rho = 1\) ويُعادل \(\ell_2\) عندما \(\rho=0\).

لاحظ أن مقياس أوزان الفئة وأوزان العينة سيؤثر على مشكلة التحسين. على سبيل المثال، ضرب أوزان العينة في ثابت \(b>0\) يُعادل ضرب قوة التنظيم (العكسية) C في \(b\).

1.1.11.2. حالة متعددة الحدود#

يمكن تمديد الحالة الثنائية إلى \(K\) فئات مما يؤدي إلى الانحدار اللوجستي متعدد الحدود، انظر أيضًا النموذج اللوغاريتمي الخطي.

ملاحظة

من الممكن تحديد معلمات نموذج تصنيف \(K\) فئة باستخدام \(K-1\) متجهات وزن فقط، وترك احتمال فئة واحدة مُحددًا تمامًا بواسطة احتمالات الفئات الأخرى من خلال الاستفادة من حقيقة أن جميع احتمالات الفئات يجب أن يصل مجموعها إلى واحد. نختار عمدًا زيادة معلمات النموذج باستخدام \(K\) متجهات وزن لسهولة التطبيق وللحفاظ على التحيز الاستقرائي المتماثل فيما يتعلق بترتيب الفئات، انظر [16]. يصبح هذا التأثير مهمًا بشكل خاص عند استخدام التنظيم. قد يكون اختيار زيادة المعلمات ضارًا بالنماذج غير المُعاقبة لأنه قد لا يكون الحل فريدًا، كما هو موضح في [16].

التفاصيل الرياضية#

افترض أن \(y_i \in {1, \ldots, K}\) هو متغير الهدف المُرمَّز (ترتيبيًا) للملاحظة \(i\). بدلاً من متجه معاملات واحد، لدينا الآن مصفوفة من المعاملات \(W\) حيث يتوافق كل متجه صف \(W_k\) مع الفئة \(k\). نهدف إلى التنبؤ باحتمالات الفئة \(P(y_i=k|X_i)\) عبر predict_proba كـ:

\[\hat{p}_k(X_i) = \frac{\exp(X_i W_k + W_{0, k})}{\sum_{l=0}^{K-1} \exp(X_i W_l + W_{0, l})}.\]

يصبح الهدف للتحسين

\[\min_W -\frac{1}{S}\sum_{i=1}^n \sum_{k=0}^{K-1} s_{ik} [y_i = k] \log(\hat{p}_k(X_i)) + \frac{r(W)}{S C}\,,\]

حيث \([P]\) يُمثل قوس إيفرسون الذي يُقيَّم إلى \(0\) إذا كان \(P\) خطأ، وإلا فإنه يُقيَّم إلى \(1\).

مرة أخرى، \(s_{ik}\) هي الأوزان التي يُعيِّنها المستخدم (ضرب أوزان العينة وأوزان الفئة) مع مجموعها \(S = \sum_{i=1}^n \sum_{k=0}^{K-1} s_{ik}\).

نُقدم حاليًا أربعة خيارات لمُصطلح التنظيم \(r(W)\) عبر وسيطة penalty، حيث \(m\) هو عدد الميزات:

penalty

\(r(W)\)

None

\(0\)

\(\ell_1\)

\(\|W\|_{1,1} = \sum_{i=1}^m\sum_{j=1}^{K}|W_{i,j}|\)

\(\ell_2\)

\(\frac{1}{2}\|W\|_F^2 = \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^{K} W_{i,j}^2\)

ElasticNet

\(\frac{1 - \rho}{2}\|W\|_F^2 + \rho \|W\|_{1,1}\)

1.1.11.3. المحللات#

المحللات المُطبقة في الفئة LogisticRegression هي "lbfgs" و "liblinear" و "newton-cg" و "newton-cholesky" و "sag" و "saga":

يُلخص الجدول التالي العقوبات ومتعدد الحدود متعدد الفئات المدعومة من قِبل كل محلل:

يتم استخدام محلل "lbfgs" افتراضيًا لمتانته. بالنسبة لمجموعات البيانات الكبيرة، عادةً ما يكون محلل "saga" أسرع. لمجموعة البيانات الكبيرة، يمكنك أيضًا التفكير في استخدام SGDClassifier مع loss="log_loss"، والذي قد يكون أسرع ولكنه يتطلب المزيد من الضبط.

1.1.11.3.1. الاختلافات بين المحللات#

قد يكون هناك اختلاف في الدرجات التي تم الحصول عليها بين LogisticRegression مع solver=liblinear أو LinearSVC ومكتبة liblinear الخارجية مباشرةً، عندما fit_intercept=False و coef_ المُناسب (أو) البيانات التي سيتم التنبؤ بها هي أصفار. هذا لأن للعينة (العينات) ذات decision_function صفر، يتنبأ LogisticRegression و LinearSVC بالفئة السالبة، بينما يتنبأ liblinear بالفئة الموجبة. لاحظ أن النموذج مع fit_intercept=False ويحتوي على العديد من العينات مع decision_function صفر، من المرجح أن يكون نموذجًا سيئًا مُفرطًا في التعميم، ويُنصح بتعيين fit_intercept=True وزيادة intercept_scaling.

تفاصيل المحللات#

  • يستخدم محلل "liblinear" خوارزمية النزول الإحداثي (CD)، ويعتمد على مكتبة C ++ LIBLINEAR الممتازة، التي يتم شحنها مع scikit-learn. ومع ذلك، لا يمكن لخوارزمية CD المُطبقة في liblinear تعلم نموذج متعدد الحدود (متعدد الفئات) حقيقي؛ بدلاً من ذلك، يتم تحليل مشكلة التحسين بطريقة "واحد مقابل البقية" لذلك يتم تدريب مُصنِّفات ثنائية مُنفصلة لجميع الفئات. يحدث هذا تحت الغطاء، لذلك تتصرف مثيلات LogisticRegression التي تستخدم هذا المحلل كمُصنِّفات متعددة الفئات. بالنسبة لتنظيم \(\ell_1\)، يسمح sklearn.svm.l1_min_c بحساب الحد الأدنى لـ C من أجل الحصول على نموذج غير "فارغ" (جميع أوزان الميزات إلى الصفر).

  • تدعم محللات "lbfgs" و "newton-cg" و "sag" فقط تنظيم \(\ell_2\) أو عدم التنظيم، ووجد أنها تتقارب بشكل أسرع بالنسبة لبعض البيانات عالية الأبعاد. يؤدي تعيين multi_class إلى "multinomial" مع هذه المحللات إلى تعلم نموذج انحدار لوجستي متعدد الحدود حقيقي [5]، مما يعني أن تقديرات احتماله يجب أن تكون مُعايرة بشكل أفضل من إعداد "واحد مقابل البقية" الافتراضي.

  • يستخدم محلل "sag" نزول التدرج العشوائي المتوسط [6]. إنه أسرع من المحللات الأخرى لمجموعات البيانات الكبيرة، عندما يكون كل من عدد العينات وعدد الميزات كبيرًا.

  • محلل "saga" [7] هو مُتغير من "sag" يدعم أيضًا penalty="l1" غير السلس. لذلك هذا هو المحلل المُفضل للانحدار اللوجستي متعدد الحدود المتفرق. وهو أيضًا المحلل الوحيد الذي يدعم penalty="elasticnet".

  • "lbfgs" هي خوارزمية تحسين تُقارب خوارزمية Broyden-Fletcher-Goldfarb-Shanno [8]، التي تنتمي إلى أساليب شبه نيوتن. على هذا النحو، يمكنها التعامل مع مجموعة واسعة من بيانات التدريب المُختلفة، وبالتالي فهي المحلل الافتراضي. ومع ذلك، فإن أدائها يُعاني على مجموعات البيانات ذات المقياس السيئ وعلى مجموعات البيانات ذات الميزات الفئوية المُرمَّزة أحاديًا مع فئات نادرة.

  • محلل "newton-cholesky" هو محلل نيوتن دقيق يحسب مصفوفة هيسيان ويحل النظام الخطي الناتج. إنه خيار جيد جدًا لـ n_samples >> n_features، لكن لديه بعض أوجه القصور: يتم دعم تنظيم \(\ell_2\) فقط. علاوة على ذلك، نظرًا لحساب مصفوفة هيسيان صراحةً، فإن استخدام الذاكرة له تبعية تربيعية على n_features وكذلك على n_classes. ونتيجة لذلك، يتم تطبيق مخطط واحد مقابل البقية فقط للحالة متعددة الفئات.

لمقارنة بعض هذه المحللات، انظر [9].

المراجع

ملاحظة

اختيار الميزات مع الانحدار اللوجستي المتفرق

يُعطي الانحدار اللوجستي مع عقوبة \(\ell_1\) نماذج متفرقة، ويمكن بالتالي استخدامه لإجراء اختيار الميزات، كما هو مُفصل في اختيار الميزات القائم على L1.

ملاحظة

تقدير قيمة p

من الممكن الحصول على قيم p وفترات ثقة لـ المعاملات في حالات الانحدار بدون عقوبة. تدعم حزمة statsmodels هذا أصلاً. داخل sklearn، يمكن للمرء استخدام التمهيد بدلاً من ذلك أيضًا.

LogisticRegressionCV يُطبق الانحدار اللوجستي مع دعم التحقق المتبادل المُدمج، لإيجاد معلمات C و l1_ratio المثلى وفقًا للسمة scoring. تم العثور على محللات "newton-cg" و "sag" و "saga" و "lbfgs" لتكون أسرع للبيانات الكثيفة عالية الأبعاد، بسبب البدء الدافئ (انظر المُصطلحات).

1.1.12. النماذج الخطية المُعممة#

تُوسِّع النماذج الخطية المُعممة (GLM) النماذج الخطية بطريقتين [10]. أولاً، ترتبط القيم المُتوقعة \(\hat{y}\) بتركيبة خطية من متغيرات الإدخال \(X\) عبر دالة ربط عكسية \(h\) كـ

\[\hat{y}(w, X) = h(Xw).\]

ثانيًا، يتم استبدال دالة الخسارة التربيعية بالانحراف الوحيد \(d\) لتوزيع في الأسرة الأسية (أو بشكل أكثر دقة، نموذج تشتت أسي تناسلي (EDM) [11]).

تصبح مشكلة التصغير:

\[\min_{w} \frac{1}{2 n_{\text{samples}}} \sum_i d(y_i, \hat{y}_i) + \frac{\alpha}{2} ||w||_2^2,\]

حيث \(\alpha\) هي عقوبة تنظيم L2. عندما يتم توفير أوزان العينة، يصبح المتوسط متوسطًا موزونًا.

يسرد الجدول التالي بعض EDMs المُحددة وانحرافها الوحيد:

يتم توضيح دوال كثافة الاحتمال (PDF) لهذه التوزيعات في الشكل التالي،

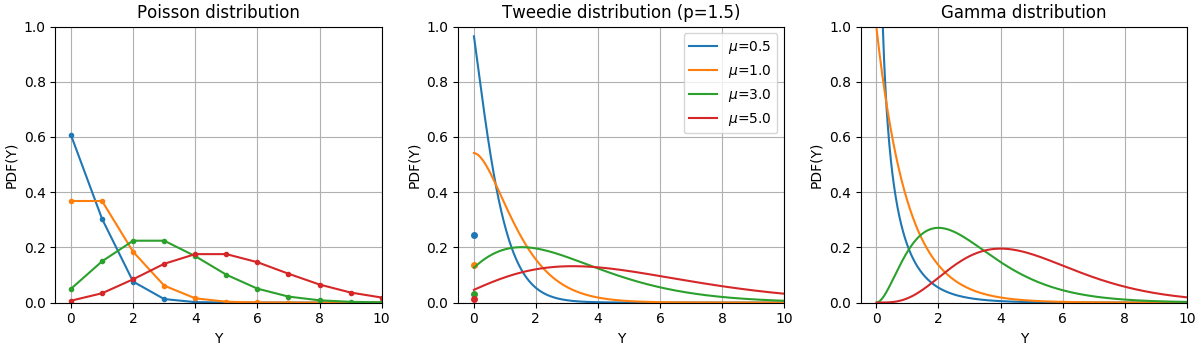
../_images/poisson_gamma_tweedie_distributions.png

PDF لمتغير عشوائي Y يتبع توزيعات بواسون وتويدي (القوة = 1.5) وجاما بقيم متوسطة مختلفة (\(\mu\)). لاحظ كتلة النقطة عند \(Y=0\) لتوزيع بواسون وتوزيع تويدي (القوة = 1.5)، ولكن ليس لتوزيع جاما الذي له مجال هدف موجب تمامًا.#

توزيع برنولي هو توزيع احتمالي منفصل يُنمذج تجربة برنولي - حدث له نتيجتان فقط متنافيتان. التوزيع الفئوي هو تعميم لتوزيع برنولي لمتغير عشوائي فئوي. بينما يحتوي متغير عشوائي في توزيع برنولي على نتيجتين مُمكنتين، يمكن لمتغير عشوائي فئوي أن يأخذ إحدى الفئات K المُمكنة، مع تحديد احتمال كل فئة بشكل مُنفصل.

يعتمد اختيار التوزيع على المشكلة المطروحة:

  • إذا كانت القيم المستهدفة \(y\) عبارة عن أعداد (ذات قيم صحيحة غير سالبة) أو ترددات نسبية (غير سالبة)، فقد تستخدم توزيع بواسون بربط سجل.

  • إذا كانت القيم المستهدفة ذات قيم موجبة ومنحرفة، فقد تُجرب توزيع جاما بربط سجل.

  • إذا بدت القيم المستهدفة أثقل من توزيع جاما، فقد تُجرب توزيع غاوسي عكسي (أو حتى قوى تباين أعلى لعائلة تويدي).

  • إذا كانت القيم المستهدفة \(y\) احتمالات، يمكنك استخدام توزيع برنولي. يمكن استخدام توزيع برنولي مع ربط logit للتصنيف الثنائي. يمكن استخدام التوزيع الفئوي مع ربط softmax لـ التصنيف متعدد الفئات.

أمثلة على حالات الاستخدام#

  • نمذجة الزراعة / الطقس: عدد أحداث المطر سنويًا (بويسون)، كمية هطول الأمطار لكل حدث (جاما)، إجمالي هطول الأمطار سنويًا (تويدي / مُركب بواسون جاما).

  • نمذجة المخاطر / تسعير بوليصة التأمين: عدد أحداث المطالبة / حامل البوليصة سنويًا (بويسون)، التكلفة لكل حدث (جاما)، التكلفة الإجمالية لكل حامل بوليصة سنويًا (تويدي / مُركب بواسون جاما).

  • التخلف عن سداد الائتمان: احتمال عدم سداد قرض (برنولي).

  • الكشف عن الاحتيال: احتمال أن تكون معاملة مالية مثل تحويل نقدي معاملة احتيالية (برنولي).

  • الصيانة التنبؤية: عدد أحداث انقطاع الإنتاج سنويًا (بويسون)، مدة الانقطاع (جاما)، إجمالي وقت الانقطاع سنويًا (تويدي / مُركب بواسون جاما).

  • اختبار الأدوية الطبية: احتمال علاج مريض في مجموعة من التجارب أو احتمال تعرض المريض لآثار جانبية (برنولي).

  • تصنيف الأخبار: تصنيف المقالات الإخبارية إلى ثلاث فئات وهي أخبار الأعمال والسياسة وأخبار الترفيه (فئوي).

المراجع

1.1.12.1. الاستخدام#

TweedieRegressor يُطبق نموذجًا خطيًا مُعممًا لـ توزيع تويدي، والذي يسمح بنمذجة أي من التوزيعات المذكورة أعلاه باستخدام معلمة power المناسبة. على وجه الخصوص:

  • power = 0: التوزيع العادي. مُقدِّرات مُحددة مثل Ridge، ElasticNet تكون أكثر ملاءمة بشكل عام في هذه الحالة.

  • power = 1: توزيع بواسون. PoissonRegressor مُعرَّض للراحة. ومع ذلك، فهو يُعادل تمامًا TweedieRegressor(power=1, link='log').

  • power = 2: توزيع جاما. GammaRegressor مُعرَّض لـ الراحة. ومع ذلك، فهو يُعادل تمامًا TweedieRegressor(power=2, link='log').

  • power = 3: التوزيع الغاوسي العكسي.

يتم تحديد دالة الربط بواسطة معلمة link.

مثال على الاستخدام:

>>> from sklearn.linear_model import TweedieRegressor
>>> reg = TweedieRegressor(power=1, alpha=0.5, link='log')
>>> reg.fit([[0, 0], [0, 1], [2, 2]], [0, 1, 2])
TweedieRegressor(alpha=0.5, link='log', power=1)
>>> reg.coef_
array([0.2463..., 0.4337...])
>>> reg.intercept_
-0.7638...

أمثلة

اعتبارات عملية#

يجب توحيد مصفوفة الميزات X قبل الملاءمة. هذا يضمن أن العقوبة تُعامل الميزات على قدم المساواة.

نظرًا لأن المُتنبئ الخطي \(Xw\) يمكن أن يكون سالبًا وبويسون و جاما والتوزيعات الغاوسية العكسية لا تدعم القيم السالبة، فمن الضروري تطبيق دالة ربط عكسية تضمن عدم السلبية. على سبيل المثال، مع link='log'، تصبح دالة الربط العكسي \(h(Xw)=\exp(Xw)\).

إذا كنت تُريد نمذجة تردد نسبي، أي عدد لكل تعرض (وقت، حجم، ...) يمكنك القيام بذلك عن طريق استخدام توزيع بواسون وتمرير \(y=\frac{\mathrm{counts}}{\mathrm{exposure}}\) كقيم مستهدفة مع \(\mathrm{exposure}\) كأوزان عينة. للحصول على مثال ملموس، انظر على سبيل المثال انحدار تويدي على مطالبات التأمين.

عند إجراء التحقق المتبادل لمعلمة power لـ TweedieRegressor، يُنصح بتحديد دالة scoring صريحة، لأن المُسجل الافتراضي TweedieRegressor.score هو دالة لـ power نفسها.

1.1.13. نزول التدرج العشوائي - SGD#

نزول التدرج العشوائي هو نهج بسيط ولكنه فعال للغاية لملاءمة النماذج الخطية. إنه مفيد بشكل خاص عندما يكون عدد العينات (وعدد الميزات) كبيرًا جدًا. يسمح أسلوب partial_fit بالتعلم على الإنترنت / خارج النواة.

تُوفر الفئات SGDClassifier و SGDRegressor وظائف لملاءمة النماذج الخطية للتصنيف والانحدار باستخدام دوال خسارة (مُحدبة) مُختلفة وعقوبات مُختلفة. على سبيل المثال، مع loss="log"، SGDClassifier يُناسب نموذج انحدار لوجستي، بينما مع loss="hinge" يُناسب آلة متجه دعم خطية (SVM).

يمكنك الرجوع إلى قسم الوثائق التحسين التدريجي العشوائي المُخصص لمزيد من التفاصيل.

1.1.14. Perceptron#

Perceptron هو خوارزمية تصنيف بسيطة أخرى مُناسبة لـ التعلم على نطاق واسع. افتراضيًا:

  • لا يتطلب مُعدل تعلم.

  • إنه غير مُنظّم (مُعاقب).

  • يُحدِّث نموذجه فقط على الأخطاء.

الخاصية الأخيرة تعني أن Perceptron أسرع قليلاً في التدريب من SGD مع خسارة المفصلة وأن النماذج الناتجة متفرقة.

في الواقع، Perceptron هو غلاف حول فئة SGDClassifier باستخدام خسارة perceptron ومُعدل تعلم ثابت. راجع القسم الرياضي لإجراء SGDلمزيد من التفاصيل.

1.1.15. خوارزميات عدوانية سلبية#

الخوارزميات العدوانية السلبية هي عائلة من الخوارزميات للتعلم واسع النطاق. إنها تُشبه Perceptron من حيث أنها لا تتطلب مُعدل تعلم. ومع ذلك، على عكس Perceptron، فإنها تتضمن معلمة تنظيم C.

للتصنيف، يمكن استخدام PassiveAggressiveClassifier مع loss='hinge' (PA-I) أو loss='squared_hinge' (PA-II). للانحدار، يمكن استخدام PassiveAggressiveRegressor مع loss='epsilon_insensitive' (PA-I) أو loss='squared_epsilon_insensitive' (PA-II).

المراجع#

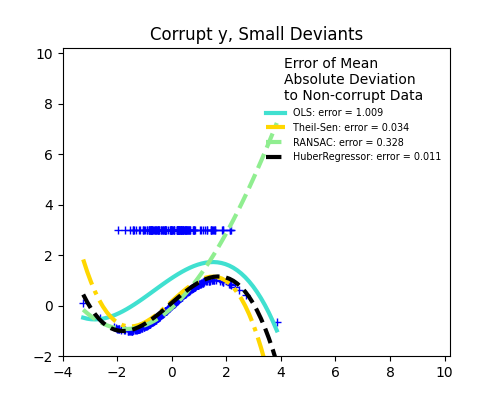
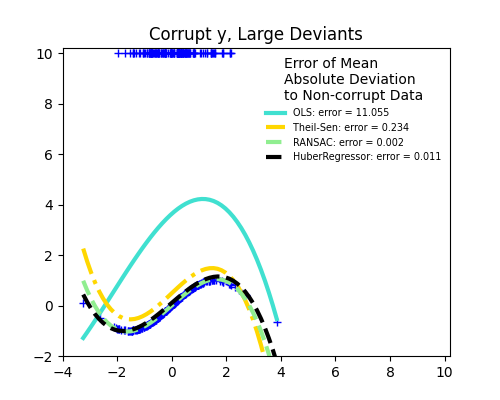
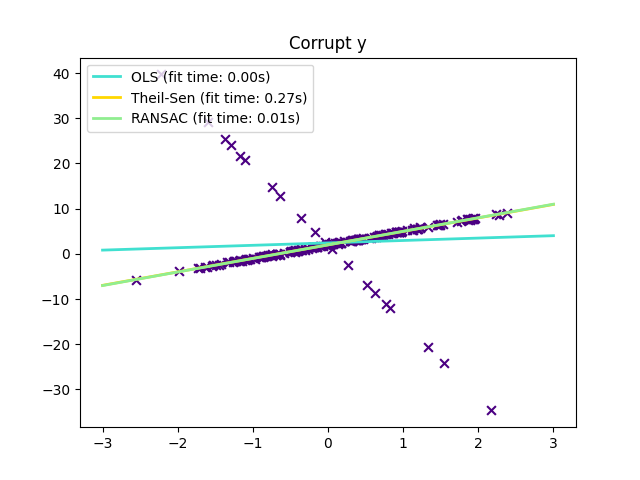
1.1.16. انحدار المتانة: القيم المتطرفة وأخطاء النمذجة#

يهدف الانحدار القوي إلى ملاءمة نموذج انحدار في وجود بيانات تالفة: إما قيم متطرفة، أو خطأ في النموذج.

../_images/sphx_glr_plot_theilsen_001.png

1.1.16.1. سيناريوهات مختلفة ومفاهيم مفيدة#

هناك أشياء مختلفة يجب وضعها في الاعتبار عند التعامل مع البيانات التالفة بواسطة القيم المتطرفة:

  • القيم المتطرفة في X أو في y؟

  • جزء القيم المتطرفة مقابل سعة الخطأ

    يهم عدد النقاط المتطرفة، ولكن أيضًا مقدار تطرفها.

    القيم المتطرفة الصغيرة

    القيم المتطرفة الكبيرة

    y_outliers

    large_y_outliers

مفهوم مهم للملاءمة القوية هو نقطة الانهيار: جزء البيانات التي يمكن أن تكون متطرفة حتى تبدأ الملاءمة في فقدان البيانات الداخلية.

لاحظ أنه بشكل عام، الملاءمة القوية في الإعداد عالي الأبعاد (كبير n_features) صعبة للغاية. من المحتمل ألا تعمل النماذج القوية هنا في هذه الإعدادات.

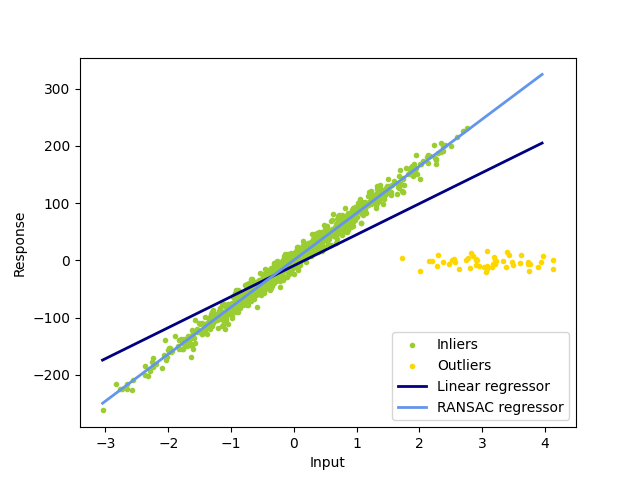
1.1.16.2. RANSAC: توافق العينة العشوائي#

يُناسب RANSAC (RANdom SAmple Consensus) نموذجًا من مجموعات فرعية عشوائية من القيم الداخلية من مجموعة البيانات الكاملة.

RANSAC هي خوارزمية غير حتمية تُنتج نتيجة معقولة فقط مع احتمالية مُعينة، والتي تعتمد على عدد التكرارات (انظر معلمة max_trials). يتم استخدامه عادةً لمشاكل الانحدار الخطي وغير الخطي وهو شائع بشكل خاص في مجال رؤية الكمبيوتر التصويرية.

تقسم الخوارزمية بيانات عينة الإدخال الكاملة إلى مجموعة من القيم الداخلية، والتي قد تخضع للضوضاء، والقيم المتطرفة، والتي تنتج على سبيل المثال عن قياسات خاطئة أو فرضيات غير صالحة حول البيانات. ثم يتم تقدير النموذج الناتج فقط من القيم الداخلية المُحددة.

../_images/sphx_glr_plot_ransac_001.png

أمثلة

تفاصيل الخوارزمية#

يُجري كل تكرار الخطوات التالية:

  1. حدد min_samples عينات عشوائية من البيانات الأصلية وتحقق مما إذا كانت مجموعة البيانات صالحة (انظر is_data_valid).

  2. قم بملاءمة نموذج على المجموعة الفرعية العشوائية (estimator.fit) وتحقق مما إذا كان النموذج المُقدَّر صالحًا (انظر is_model_valid).

  3. صنف جميع البيانات على أنها قيم داخلية أو قيم متطرفة عن طريق حساب البواقي إلى النموذج المُقدَّر (estimator.predict(X) - y) - جميع عينات البيانات ذات البواقي المُطلقة الأصغر من أو تساوي residual_threshold تُعتبر قيمًا داخلية.

  4. احفظ النموذج المُناسب كأفضل نموذج إذا كان عدد عينات القيم الداخلية أقصى. في حالة احتواء النموذج المُقدَّر الحالي على نفس عدد القيم الداخلية، فإنه يُعتبر فقط كأفضل نموذج إذا كان لديه درجة أفضل.

يتم تنفيذ هذه الخطوات إما لعدد أقصى من المرات (max_trials) أو حتى يتم استيفاء أحد معايير الإيقاف الخاصة (انظر stop_n_inliers و stop_score). يتم تقدير النموذج النهائي باستخدام جميع عينات القيم الداخلية (مجموعة التوافق) لأفضل نموذج مُحدد مسبقًا.

تسمح الدالتان is_data_valid و is_model_valid بتحديد ورفض مجموعات عينات فرعية عشوائية مُتدهورة. إذا لم يكن النموذج المُقدَّر مطلوبًا لتحديد الحالات المتدهورة، فيجب استخدام is_data_valid حيث يتم استدعاؤه قبل ملاءمة النموذج، مما يؤدي إلى أداء حسابي أفضل.

المراجع#

1.1.16.3. مُقدِّر Theil-Sen: مُقدِّر قائم على الوسيط المُعمم#

يستخدم مُقدِّر TheilSenRegressor تعميمًا للوسيط في أبعاد متعددة. وبالتالي فهو قوي ضد القيم المتطرفة متعددة المتغيرات. لاحظ ومع ذلك أن قوة المُقدِّر تتناقص بسرعة مع أبعاد المشكلة. يفقد خصائص المتانة الخاصة به ويصبح ليس أفضل من المربعات الصغرى العادية في البُعد العالي.

أمثلة

اعتبارات نظرية#

TheilSenRegressor مُقارن لـ المربعات الصغرى العادية (OLS) من حيث الكفاءة المقاربة وكمُقدِّر غير مُتحيز. على عكس OLS، فإن Theil-Sen هو أسلوب غير معلمي مما يعني أنه لا يضع أي افتراض حول التوزيع الأساسي للبيانات. نظرًا لأن Theil-Sen هو مُقدِّر قائم على الوسيط، فإنه أكثر قوة ضد البيانات التالفة المعروفة أيضًا باسم القيم المتطرفة. في إعداد أحادي المتغير، Theil-Sen لديه نقطة انهيار تبلغ حوالي 29.3% في حالة الانحدار الخطي البسيط مما يعني أنه يمكنه تحمل بيانات تالفة عشوائية تصل إلى 29.3%.

../_images/sphx_glr_plot_theilsen_001.png

يتبع تطبيق TheilSenRegressor في scikit-learn تعميمًا لنموذج الانحدار الخطي متعدد المتغيرات [14] باستخدام الوسيط المكاني وهو تعميم للوسيط لأبعاد متعددة [15].

من حيث تعقيد الوقت والمساحة، يتناسب Theil-Sen وفقًا لـ

\[\binom{n_{\text{samples}}}{n_{\text{subsamples}}}\]

مما يجعله غير مُجدي للتطبيق بشكل شامل على المشاكل التي تحتوي على عدد كبير من العينات والميزات. لذلك، يمكن اختيار حجم مجموعة فرعية لتقييد تعقيد الوقت والمساحة عن طريق النظر فقط في مجموعة فرعية عشوائية من جميع التوليفات الممكنة.

المراجع

انظر أيضًا صفحة ويكيبيديا

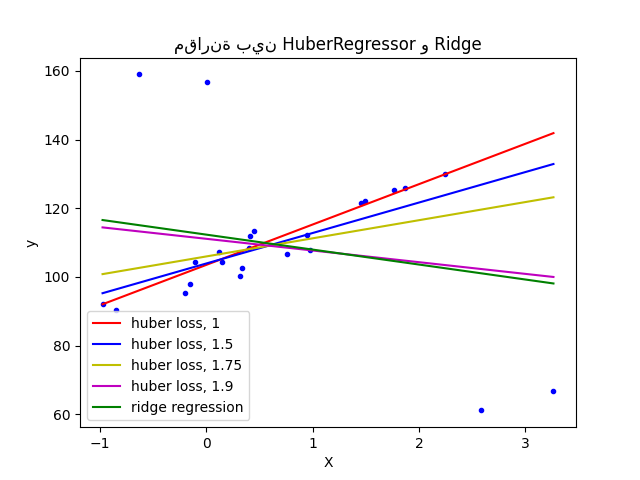
1.1.16.4. انحدار Huber#

يختلف HuberRegressor عن Ridge لأنه يُطبق خسارة خطية على العينات التي تُصنف على أنها قيم متطرفة. يتم تصنيف عينة على أنها قيمة داخلية إذا كان الخطأ المُطلق لتلك العينة أقل من عتبة مُعينة. إنه يختلف عن TheilSenRegressor و RANSACRegressor لأنه لا يتجاهل تأثير القيم المتطرفة ولكنه يُعطي وزنًا أقل لها.

../_images/sphx_glr_plot_huber_vs_ridge_001.png

أمثلة

التفاصيل الرياضية#

دالة الخسارة التي يُقللها HuberRegressor مُعطاة بواسطة

\[\min_{w, \sigma} {\sum_{i=1}^n\left(\sigma + H_{\epsilon}\left(\frac{X_{i}w - y_{i}}{\sigma}\right)\sigma\right) + \alpha {||w||_2}^2}\]

حيث

\[\begin{split}H_{\epsilon}(z) = \begin{cases} z^2, & \text {if } |z| < \epsilon, \\ 2\epsilon|z| - \epsilon^2, & \text{otherwise} \end{cases}\end{split}\]

يُنصح بتعيين المعلمة epsilon إلى 1.35 لتحقيق كفاءة إحصائية بنسبة 95%.

المراجع

  • Peter J. Huber, Elvezio M. Ronchetti: Robust Statistics, Concomitant scale estimates, pg 172

يختلف HuberRegressor عن استخدام SGDRegressor مع تعيين الخسارة إلى huber بالطرق التالية.

  • HuberRegressor ثابت المقياس. بمجرد تعيين epsilon، فإن تغيير مقياس X و y لأعلى أو لأسفل بقيم مُختلفة سيُنتج نفس المتانة للقيم المتطرفة كما كان من قبل. مُقارنةً بـ SGDRegressor حيث يجب تعيين epsilon مرة أخرى عند تغيير مقياس X و y.

  • يجب أن يكون HuberRegressor أكثر كفاءة في الاستخدام على البيانات ذات العدد القليل من العينات بينما يحتاج SGDRegressor إلى عدد من التمريرات على بيانات التدريب لـ إنتاج نفس المتانة.

لاحظ أن هذا المُقدِّر يختلف عن تطبيق R للانحدار القوي (https://stats.oarc.ucla.edu/r/dae/robust-regression/) لأن تطبيق R يُجري تطبيقًا للمربعات الصغرى الموزونة بأوزان مُعطاة لكل عينة على أساس مقدار الباقي أكبر من عتبة مُعينة.

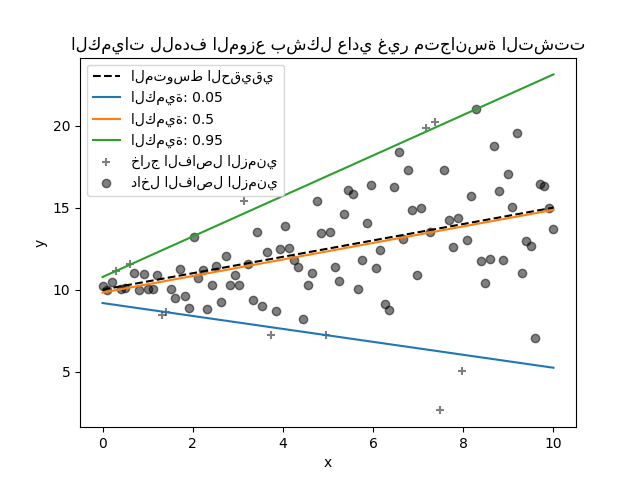
1.1.17. انحدار المُكمِّم#

يُقدِّر انحدار المُكمِّم الوسيط أو مُكمِّمات أخرى لـ \(y\) الشرطية على \(X\)، بينما تُقدِّر المربعات الصغرى العادية (OLS) المتوسط الشرطي.

قد يكون انحدار المُكمِّم مفيدًا إذا كان المرء مهتمًا بالتنبؤ بـ فاصل زمني بدلاً من التنبؤ بالنقطة. في بعض الأحيان، يتم حساب فترات التنبؤ بناءً على افتراض أن خطأ التنبؤ موزع بشكل طبيعي بمتوسط صفري وتباين ثابت. يُوفر انحدار المُكمِّم فترات تنبؤ معقولة حتى للأخطاء ذات التباين غير الثابت (ولكن التنبؤي) أو التوزيع غير العادي.

../_images/sphx_glr_plot_quantile_regression_002.png

بناءً على تقليل خسارة الكرة والدبوس، يمكن أيضًا تقدير المُكمِّمات الشرطية بواسطة نماذج أخرى غير النماذج الخطية. على سبيل المثال، GradientBoostingRegressor يمكنه التنبؤ بـ مُكمِّمات شرطية إذا تم تعيين معلمته loss إلى "quantile" وتم تعيين المعلمة alpha إلى المُكمِّم الذي يجب التنبؤ به. انظر المثال في فترات التنبؤ لانحدار التعزيز المتدرج.

تعتمد معظم تطبيقات انحدار المُكمِّم على مشكلة البرمجة الخطية. يعتمد التطبيق الحالي على scipy.optimize.linprog.

أمثلة

التفاصيل الرياضية#

كنموذج خطي، يُعطي QuantileRegressor تنبؤات خطية \(\hat{y}(w, X) = Xw\) لـ \(q\)-th مُكمِّم، \(q \in (0, 1)\). ثم يتم إيجاد الأوزان أو المعاملات \(w\) بواسطة مشكلة التصغير التالية:

\[\min_{w} {\frac{1}{n_{\text{samples}}} \sum_i PB_q(y_i - X_i w) + \alpha ||w||_1}.\]

يتكون هذا من خسارة الكرة والدبوس (المعروفة أيضًا باسم الخسارة الخطية)، انظر أيضًا mean_pinball_loss،

\[\begin{split}PB_q(t) = q \max(t, 0) + (1 - q) \max(-t, 0) = \begin{cases} q t, & t > 0, \\ 0, & t = 0, \\ (q-1) t, & t < 0 \end{cases}\end{split}\]

وعقوبة L1 التي تتحكم فيها المعلمة alpha، على غرار Lasso.

نظرًا لأن خسارة الكرة والدبوس خطية فقط في البواقي، فإن انحدار المُكمِّم أكثر قوة ضد القيم المتطرفة من التقدير القائم على الخطأ التربيعي للمتوسط. في مكان ما بينهما هو HuberRegressor.

المراجع#

1.1.18. الانحدار متعدد الحدود: توسيع النماذج الخطية مع دوال الأساس#

أحد الأنماط الشائعة في التعلم الآلي هو استخدام النماذج الخطية المُدرَّبة على دوال غير خطية للبيانات. يحافظ هذا النهج على الأداء السريع بشكل عام للطرق الخطية، مع السماح لها بملاءمة نطاق أوسع بكثير من البيانات.

التفاصيل الرياضية#

على سبيل المثال، يمكن تمديد انحدار خطي بسيط عن طريق بناء ميزات متعددة الحدود من المعاملات. في حالة الانحدار الخطي القياسية، قد يكون لديك نموذج يبدو كالتالي لـ بيانات ثنائية الأبعاد:

\[\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2\]

إذا أردنا ملاءمة قطع مكافئ للبيانات بدلاً من مستوى، فيمكننا دمج الميزات في كثيرات حدود من الدرجة الثانية، بحيث يبدو النموذج على النحو التالي:

\[\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_1 x_2 + w_4 x_1^2 + w_5 x_2^2\]

الملاحظة (المُفاجئة أحيانًا) هي أن هذا لا يزال نموذجًا خطيًا: لرؤية ذلك، تخيل إنشاء مجموعة جديدة من الميزات

\[z = [x_1, x_2, x_1 x_2, x_1^2, x_2^2]\]

مع إعادة تسمية البيانات هذه، يمكن كتابة مشكلتنا

\[\hat{y}(w, z) = w_0 + w_1 z_1 + w_2 z_2 + w_3 z_3 + w_4 z_4 + w_5 z_5\]

نرى أن الانحدار متعدد الحدود الناتج في نفس فئة النماذج الخطية التي نظرنا فيها أعلاه (أي أن النموذج خطي في \(w\)) ويمكن حله بنفس التقنيات. بالنظر إلى الملاءمات الخطية داخل فضاء ذي أبعاد أعلى مبني باستخدام دوال الأساس هذه، يتمتع النموذج بالمرونة لملاءمة نطاق أوسع بكثير من البيانات.

فيما يلي مثال على تطبيق هذه الفكرة على بيانات أحادية البعد، باستخدام ميزات متعددة الحدود بدرجات مُتفاوتة:

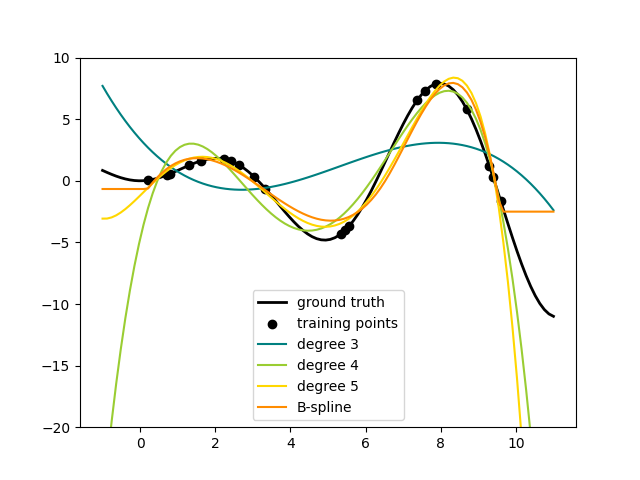
../_images/sphx_glr_plot_polynomial_interpolation_001.png

يتم إنشاء هذا الشكل باستخدام مُحوِّل PolynomialFeatures، الذي يُحوِّل مصفوفة بيانات الإدخال إلى مصفوفة بيانات جديدة من درجة مُعطاة. يمكن استخدامه على النحو التالي:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

تم تحويل ميزات X من \([x_1, x_2]\) إلى \([1, x_1, x_2, x_1^2, x_1 x_2, x_2^2]\)، ويمكن الآن استخدامها داخل أي نموذج خطي.

يمكن تبسيط هذا النوع من المُعالجة المُسبقة باستخدام أدوات Pipeline. يمكن إنشاء كائن واحد يُمثِّل انحدارًا متعدد الحدود بسيطًا واستخدامه على النحو التالي:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
...                   ('linear', LinearRegression(fit_intercept=False))])
>>> # ملاءمة بيانات متعددة الحدود من الرتبة 3
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2.,  1., -1.])

النموذج الخطي المُدرَّب على الميزات متعددة الحدود قادر على استرداد معاملات مُتعددة الحدود المدخلة بدقة.

في بعض الحالات، ليس من الضروري تضمين قوى أعلى لأي ميزة فردية، ولكن فقط ما يُسمى ميزات التفاعل التي تضرب معًا \(d\) ميزات مُتميزة على الأكثر. يمكن الحصول على هذه من PolynomialFeatures مع الإعداد interaction_only=True.

على سبيل المثال، عند التعامل مع ميزات منطقية، \(x_i^n = x_i\) لجميع \(n\) وبالتالي فهي غير مُجدية؛ لكن \(x_i x_j\) يُمثل اقتران اثنين من القيم المنطقية. بهذه الطريقة، يمكننا حل مشكلة XOR باستخدام مُصنف خطي:

>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
       [1, 0, 1, 0],
       [1, 1, 0, 0],
       [1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, max_iter=10, tol=None,
...                  shuffle=False).fit(X, y)

وتنبؤات المُصنف "مثالية":

>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0
On this page
إظهار المصدر