2.6. تقدير التباين المشترك

تتطلب العديد من المشكلات الإحصائية تقدير مصفوفة التباين المشترك لمجموعة سكانية، والتي يمكن اعتبارها تقديرًا لشكل مخطط تشتت مجموعة البيانات. في معظم الأوقات، يجب إجراء مثل هذا التقدير على عينة لها خصائص (الحجم، الهيكل، التجانس) لها تأثير كبير على جودة التقدير. توفر حزمة sklearn.covariance أدوات لتقدير مصفوفة التباين المشترك لمجموعة سكانية بدقة في ظل إعدادات مختلفة.

نفترض أن الملاحظات مستقلة وموزعة بشكل متماثل (i.i.d.).

2.6.1. التباين المشترك التجريبي

من المعروف أن مصفوفة التباين المشترك لمجموعة البيانات يتم تقريبها جيدًا بواسطة مقدر الاحتمالية القصوى الكلاسيكي (أو "التباين المشترك التجريبي")، بشرط أن يكون عدد الملاحظات كبيرًا بما يكفي مقارنة بعدد الميزات (المتغيرات التي تصف الملاحظات). بتعبير أدق، فإن مقدر الاحتمالية القصوى للعينة هو مقدر غير متحيز مقارب لمصفوفة التباين المشترك للسكان المقابلة.

يمكن حساب مصفوفة التباين المشترك التجريبي للعينة باستخدام دالة empirical_covariance للحزمة، أو عن طريق ملاءمة كائن EmpiricalCovariance لعينة البيانات باستخدام طريقة EmpiricalCovariance.fit. كن حذرًا من أن النتائج تعتمد على ما إذا كانت البيانات متمركزة، لذلك قد يرغب المرء في استخدام معلمة assume_centered بدقة. بتعبير أدق، إذا كان assume_centered=False، فمن المفترض أن يكون لمجموعة الاختبار نفس متجه المتوسط مثل مجموعة التدريب. إذا لم يكن الأمر كذلك، فيجب أن يكون كلاهما متمركزًا بواسطة المستخدم، ويجب استخدام assume_centered=True.

أمثلة

• انظر sphx_glr_auto_examples_covariance/plot_covariance_estimation.py للحصول على مثال حول كيفية ملاءمة كائن EmpiricalCovariance للبيانات.

2.6.2. التباين المشترك المنكمش

2.6.2.1. الانكماش الأساسي

على الرغم من كونه مقدرًا غير متحيز مقارب لمصفوفة التباين المشترك، فإن مقدر الاحتمالية القصوى ليس مقدرًا جيدًا لقيم eigenvalues لمصفوفة التباين المشترك، لذلك فإن مصفوفة الدقة التي تم الحصول عليها من انعكاسها ليست دقيقة. في بعض الأحيان، يحدث حتى أنه لا يمكن عكس مصفوفة التباين المشترك التجريبية لأسباب رقمية. لتجنب مشكلة الانعكاس هذه، تم إدخال تحويل لمصفوفة التباين المشترك التجريبية: الانكماش.

في scikit-learn، يمكن تطبيق هذا التحويل (مع معامل انكماش محدد من قبل المستخدم) مباشرة على التباين المشترك المحسوب مسبقًا باستخدام طريقة shrunk_covariance. أيضًا، يمكن ملاءمة مقدر منكمش للتباين المشترك مع البيانات باستخدام كائن ShrunkCovariance وطرقه ShrunkCovariance.fit. مرة أخرى، تعتمد النتائج على ما إذا كانت البيانات متمركزة، لذلك قد يرغب المرء في استخدام معلمة assume_centered بدقة.

رياضيًا، يتكون هذا الانكماش في تقليل النسبة بين أصغر وأكبر قيم eigenvalues لمصفوفة التباين المشترك التجريبية. يمكن القيام بذلك ببساطة عن طريق تحويل كل eigenvalue وفقًا لإزاحة معينة، وهو ما يعادل إيجاد مقدر الاحتمالية القصوى المعاقب بـ l2 لمصفوفة التباين المشترك. من الناحية العملية، يتلخص الانكماش في تحويل محدب بسيط:

\(\Sigma_{\rm shrunk} = (1-\alpha)\hat{\Sigma} + \alpha\frac{{\rm Tr}\hat{\Sigma}}{p}\rm Id\).

اختيار مقدار الانكماش، \(\alpha\) يرقى إلى تعيين مقايضة التحيز / التباين، ويتم مناقشته أدناه.

أمثلة

• انظر sphx_glr_auto_examples_covariance/plot_covariance_estimation.py للحصول على مثال حول كيفية ملاءمة كائن ShrunkCovariance للبيانات.

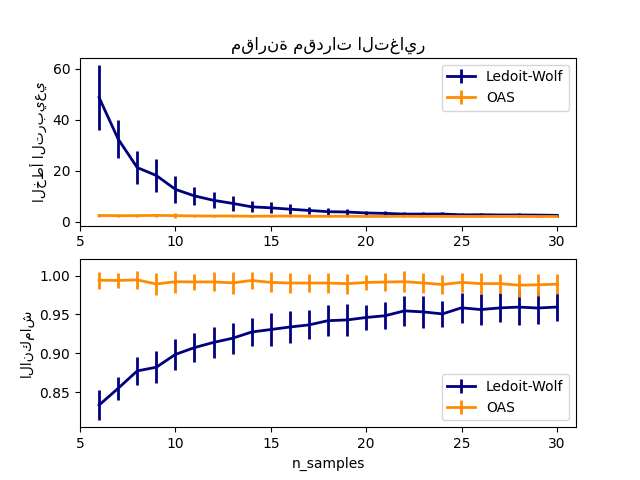
2.6.2.2. انكماش Ledoit-Wolf

في ورقتهم البحثية لعام 2004 [1]، اقترح O. Ledoit و M. Wolf صيغة لحساب معامل الانكماش الأمثل \(\alpha\) الذي يقلل من متوسط الخطأ التربيعي بين مصفوفة التباين المشترك المقدرة والحقيقية.

يمكن حساب مقدر Ledoit-Wolf لمصفوفة التباين المشترك على عينة باستخدام طريقة ledoit_wolf لحزمة sklearn.covariance، أو يمكن الحصول عليها بطريقة أخرى عن طريق ملاءمة كائن LedoitWolf لنفس العينة.

ملاحظة

الحالة عندما تكون مصفوفة التباين المشترك للسكان متجانسة الخواص

من المهم ملاحظة أنه عندما يكون عدد العينات أكبر بكثير من عدد الميزات، يتوقع المرء ألا يكون الانكماش ضروريًا. الحدس وراء ذلك هو أنه إذا كان التباين المشترك للسكان كامل الرتبة، فعندما يزداد عدد العينات، سيصبح التباين المشترك للعينة أيضًا موجبًا محددًا. ونتيجة لذلك، لن يكون الانكماش ضروريًا ويجب أن تفعل الطريقة ذلك تلقائيًا.

ومع ذلك، ليس هذا هو الحال في إجراء Ledoit-Wolf عندما يكون التباين المشترك للسكان مضاعفًا لمصفوفة الهوية. في هذه الحالة، يقترب تقدير انكماش Ledoit-Wolf من 1 مع زيادة عدد العينات. يشير هذا إلى أن التقدير الأمثل لمصفوفة التباين المشترك بمعنى Ledoit-Wolf هو مضاعف الهوية. نظرًا لأن التباين المشترك للسكان هو بالفعل مضاعف لمصفوفة الهوية، فإن حل Ledoit-Wolf هو بالفعل تقدير معقول.

أمثلة

• انظر sphx_glr_auto_examples_covariance/plot_covariance_estimation.py للحصول على مثال حول كيفية ملاءمة كائن LedoitWolf للبيانات ولتصور أداء مقدر Ledoit-Wolf من حيث الاحتمالية.

المراجع

[1]

O. Ledoit and M. Wolf, "A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices", Journal of Multivariate Analysis, Volume 88, Issue 2, February 2004, pages 365-411.

2.6.2.3. انكماش تقريب أوراكل

بافتراض أن البيانات موزعة بشكل غاوسي، اشتق Chen وآخرون [2] صيغة تهدف إلى اختيار معامل انكماش ينتج عنه متوسط خطأ تربيعي أصغر من ذلك الذي قدمته صيغة Ledoit و Wolf. يُعرف المقدر الناتج باسم مقدر تقريب انكماش أوراكل للتباين المشترك.

يمكن حساب مقدر OAS لمصفوفة التباين المشترك على عينة باستخدام طريقة oas لحزمة sklearn.covariance، أو يمكن الحصول عليها بطريقة أخرى عن طريق ملاءمة كائن OAS لنفس العينة.

مقايضة التحيز / التباين عند تعيين الانكماش: مقارنة اختيارات مقدرات Ledoit-Wolf و OAS

المراجع

[2]

"Shrinkage algorithms for MMSE covariance estimation.", Chen, Y., Wiesel, A., Eldar, Y. C., & Hero, A. O. IEEE Transactions on Signal Processing, 58(10), 5016-5029, 2010.

أمثلة

• انظر sphx_glr_auto_examples_covariance/plot_covariance_estimation.py للحصول على مثال حول كيفية ملاءمة كائن OAS للبيانات.

• انظر sphx_glr_auto_examples_covariance/plot_lw_vs_oas.py لتصور فرق متوسط الخطأ التربيعي بين LedoitWolf و OAS مقدر للتباين المشترك.

2.6.3. التباين المشترك العكسي المتناثر

إن معكوس المصفوفة لمصفوفة التباين المشترك، والتي غالبًا ما تسمى مصفوفة الدقة، تتناسب مع مصفوفة الارتباط الجزئي. يعطي علاقة الاستقلال الجزئي. بمعنى آخر، إذا كانت ميزتان مستقلتين بشكل مشروط على الأخريين، فسيكون المعامل المقابل في مصفوفة الدقة صفرًا. هذا هو السبب في أنه من المنطقي تقدير مصفوفة دقة متفرقة: يكون تقدير مصفوفة التباين المشترك أفضل من خلال تعلم علاقات الاستقلال من البيانات. يُعرف هذا باسم اختيار التباين المشترك.

في حالة العينات الصغيرة، حيث يكون n_samples بترتيب n_features أو أصغر، تميل مقدرات التباين المشترك العكسي المتناثر إلى العمل بشكل أفضل من مقدرات التباين المشترك المنكمش. ومع ذلك، في الحالة المعاكسة، أو للبيانات المترابطة للغاية، يمكن أن تكون غير مستقرة عدديًا. بالإضافة إلى ذلك، على عكس مقدرات الانكماش، فإن المقدرات المتفرقة قادرة على استعادة الهيكل خارج القطر.

يستخدم مقدر GraphicalLasso عقوبة l1 لفرض التباين على مصفوفة الدقة: كلما زادت معلمة alpha، زادت تباين مصفوفة الدقة. يستخدم كائن GraphicalLassoCV المقابل التحقق المتبادل لتعيين معلمة alpha تلقائيًا.

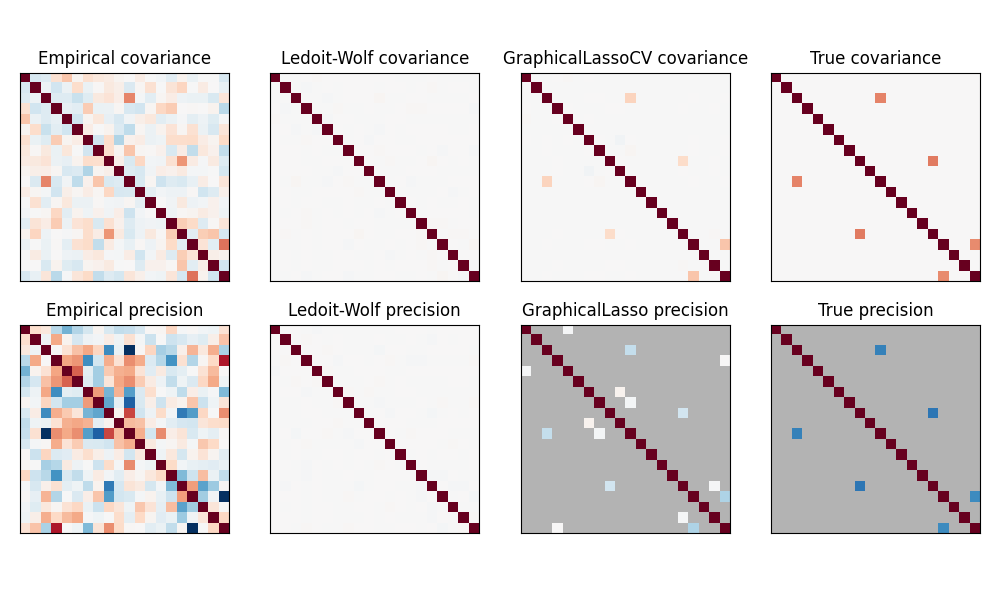
مقارنة بين الاحتمالية القصوى والانكماش والتقديرات المتفرقة للتباين المشترك ومصفوفة الدقة في إعدادات العينات الصغيرة جدًا.

ملاحظة

استعادة الهيكل

إن استعادة بنية رسومية من الارتباطات في البيانات أمر صعب. إذا كنت مهتمًا بهذا الاسترداد، ضع في اعتبارك ما يلي:

• يكون الاسترداد أسهل من مصفوفة الارتباط من مصفوفة التباين المشترك: قم بتوحيد ملاحظاتك قبل تشغيل GraphicalLasso

• إذا كان الرسم البياني الأساسي يحتوي على عقد ذات اتصالات أكثر بكثير من العقدة المتوسطة، فستفقد الخوارزمية بعض هذه الاتصالات.

• إذا لم يكن عدد ملاحظاتك كبيرًا مقارنة بعدد الحواف في الرسم البياني الأساسي، فلن تستعيدها.

• حتى إذا كنت في ظروف استرداد مواتية، فإن معلمة alpha التي تم اختيارها عن طريق التحقق المتبادل (على سبيل المثال باستخدام كائن GraphicalLassoCV) ستؤدي إلى تحديد عدد كبير جدًا من الحواف. ومع ذلك، سيكون للحواف ذات الصلة أوزان أثقل من الحواف غير ذات الصلة.

الصيغة الرياضية هي كما يلي:

\[\hat{K} = \mathrm{argmin}_K \big( \mathrm{tr} S K - \mathrm{log} \mathrm{det} K + \alpha \|K\|_1 \big)\]

حيث \(K\) هي مصفوفة الدقة المراد تقديرها، و \(S\) هي مصفوفة التباين المشترك للعينة. \(\|K\|_1\) هو مجموع القيم المطلقة للمعاملات خارج القطر لـ \(K\). الخوارزمية المستخدمة لحل هذه المشكلة هي خوارزمية GLasso، من ورقة Friedman 2008 Biostatistics. إنها نفس الخوارزمية الموجودة في حزمة R glasso.

أمثلة

• sphx_glr_auto_examples_covariance/plot_sparse_cov.py: مثال على البيانات التركيبية يوضح بعض استعادة الهيكل، ومقارنته بمقدرات التباين المشترك الأخرى.

• sphx_glr_auto_examples_applications/plot_stock_market.py: مثال على بيانات سوق الأسهم الحقيقية، والعثور على الرموز الأكثر ارتباطًا.

المراجع

• Friedman et al, "Sparse inverse covariance estimation with the graphical lasso"، Biostatistics 9، pp 432، 2008

2.6.4. تقدير التباين المشترك القوي

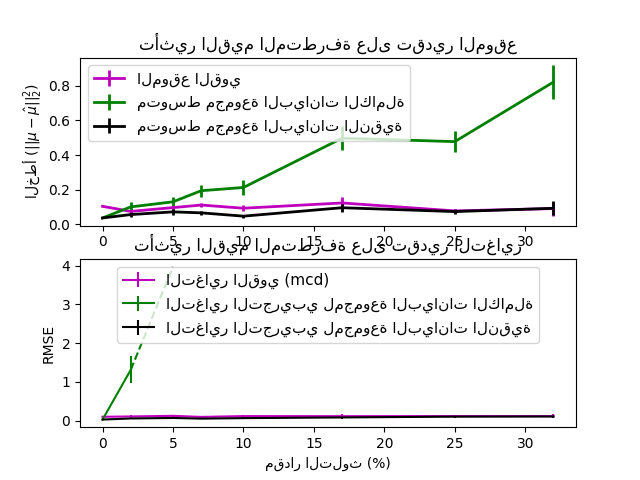
غالبًا ما تخضع مجموعات البيانات الحقيقية لأخطاء القياس أو التسجيل. قد تظهر أيضًا ملاحظات منتظمة ولكنها غير شائعة لعدة أسباب. تسمى الملاحظات غير الشائعة جدًا بالقيم المتطرفة. مقدر التباين المشترك التجريبي ومقدرات التباين المشترك المنكمش المقدمة أعلاه حساسة للغاية لوجود القيم المتطرفة في البيانات. لذلك، يجب على المرء استخدام مقدرات التباين المشترك القوية لتقدير التباين المشترك لمجموعات البيانات الحقيقية الخاصة به. بدلاً من ذلك، يمكن استخدام مقدرات التباين المشترك القوية لإجراء اكتشاف القيم المتطرفة والتخلص من / تقليل بعض الملاحظات وفقًا للمعالجة الإضافية للبيانات.

تنفذ حزمة sklearn.covariance مقدرًا قويًا للتباين المشترك، وهو محدد التباين المشترك الأدنى [3].

2.6.4.1. محدد التباين المشترك الأدنى

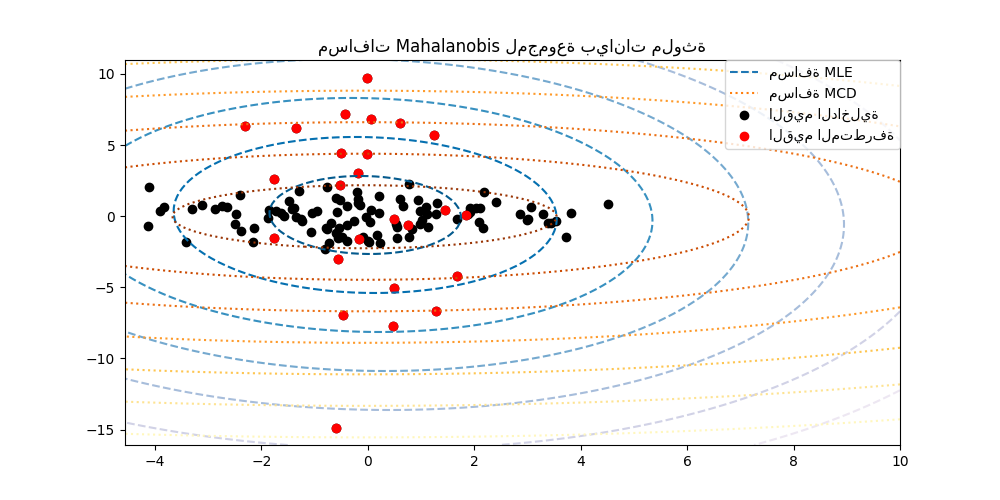
مقدر محدد التباين المشترك الأدنى هو مقدر قوي للتباين المشترك لمجموعة البيانات قدمه P.J. Rousseeuw في [3]. الفكرة هي إيجاد نسبة معينة (h) من الملاحظات "الجيدة" التي ليست قيمًا متطرفة وحساب مصفوفة التباين المشترك التجريبية الخاصة بها. ثم يتم إعادة قياس مصفوفة التباين المشترك التجريبية هذه لتعويض الاختيار الذي تم إجراؤه للملاحظات ("خطوة الاتساق"). بعد حساب مقدر محدد التباين المشترك الأدنى، يمكن للمرء إعطاء أوزان للملاحظات وفقًا لمسافة Mahalanobis الخاصة بهم، مما يؤدي إلى تقدير معاد وزنه لمصفوفة التباين المشترك لمجموعة البيانات ("خطوة إعادة الوزن").

طور Rousseeuw و Van Driessen [4] خوارزمية FastMCD من أجل حساب محدد التباين المشترك الأدنى. تستخدم هذه الخوارزمية في scikit-learn عند ملاءمة كائن MCD للبيانات. تحسب خوارزمية FastMCD أيضًا تقديرًا قويًا لموقع مجموعة البيانات في نفس الوقت.

يمكن الوصول إلى التقديرات الأولية كسمات raw_location_ و raw_covariance_ لكائن مقدر التباين المشترك القوي MinCovDet.

المراجع

[3] (1,2)

P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass، 79: 871، 1984.

[4]

A Fast Algorithm for the Minimum Covariance Determinant Estimator، 1999، الرابطة الإحصائية الأمريكية والجمعية الأمريكية للجودة، TECHNOMETRICS.

أمثلة

• انظر sphx_glr_auto_examples_covariance/plot_robust_vs_empirical_covariance.py للحصول على مثال حول كيفية ملاءمة كائن MinCovDet للبيانات ومعرفة كيف يظل التقدير دقيقًا على الرغم من وجود القيم المتطرفة.

• انظر sphx_glr_auto_examples_covariance/plot_mahalanobis_distances.py لتصور الفرق بين مقدرات التباين المشترك EmpiricalCovariance و MinCovDet من حيث مسافة Mahalanobis (لذلك نحصل على تقدير أفضل لمصفوفة الدقة أيضًا).

---

تأثير القيم المتطرفة على تقديرات الموقع والتباين المشترك	فصل القيم الداخلية عن القيم المتطرفة باستخدام مسافة Mahalanobis