2.9. نماذج الشبكة العصبية (غير خاضعة للإشراف)#
2.9.1. آلات بولتزمان المُقيّدة#
آلات بولتزمان المُقيّدة (RBM) هي أدوات تعلم ميزات غير خطية وغير خاضعة للإشراف تعتمد على نموذج احتمالي. غالبًا ما تُعطي الميزات التي يتم استخراجها بواسطة RBM أو تسلسل هرمي من RBMs نتائج جيدة عند تغذيتها في مُصنف خطي مثل SVM خطي أو بيرسيبترون.
يضع النموذج افتراضات بخصوص توزيع المدخلات. في الوقت الحالي، تُوفر scikit-learn فقط BernoulliRBM، التي تفترض أن المدخلات هي إما قيم ثنائية أو قيم بين 0 و 1، كل منها يُشفّر احتمال تشغيل الميزة المُحدّدة.
تحاول RBM تعظيم احتمالية البيانات باستخدام نموذج رسومي مُحدّد. تمنع خوارزمية تعلم المعلمات المُستخدمة (أقصى احتمالية عشوائية) التمثيلات من الابتعاد كثيرًا عن بيانات الإدخال، مما يجعلها تلتقط انتظامات مثيرة للاهتمام، ولكنه يجعل النموذج أقل فائدة لمجموعات البيانات الصغيرة، وعادةً ما يكون غير مفيد لتقدير الكثافة.
اكتسبت الطريقة شعبية لتهيئة الشبكات العصبية العميقة بأوزان RBMs مستقلة. تُعرف هذه الطريقة باسم التدريب المُسبق غير الخاضع للإشراف.

أمثلة
2.9.1.1. النموذج الرسومي والمعلمات#
النموذج الرسومي لـ RBM هو رسم بياني ثنائي الأجزاء مُتصل بالكامل.
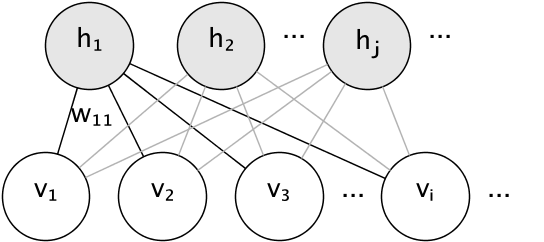
العقد هي متغيرات عشوائية تعتمد حالتها على حالة العقد الأخرى التي تتصل بها. لذلك، يتم تحديد معلمات النموذج بواسطة أوزان الاتصالات، بالإضافة إلى مصطلح تقاطع واحد (انحياز) لكل وحدة مرئية ومخفية، تم حذفه من الصورة من أجل التبسيط.
تقيس دالة الطاقة جودة التعيين المُشترك:
في الصيغة أعلاه، \(\mathbf{b}\) و \(\mathbf{c}\) هما متجها التقاطع للطبقات المرئية والمخفية، على التوالي. يتم تعريف الاحتمال المُشترك للنموذج من حيث الطاقة:
تشير كلمة مُقيّد إلى بنية ثنائية الأجزاء للنموذج، والتي تمنع التفاعل المُباشر بين الوحدات المخفية، أو بين الوحدات المرئية. هذا يعني أنه يتم افتراض الاستقلالية الشرطية التالية:
تسمح البنية ثنائية الأجزاء باستخدام أخذ عينات جيبس الكتل الفعال للاستدلال.
2.9.1.2. آلات بولتزمان المُقيّدة لبرنولي#
في BernoulliRBM، جميع الوحدات هي وحدات عشوائية ثنائية. هذا يعني أنه يجب أن تكون بيانات الإدخال إما ثنائية، أو ذات قيمة حقيقية بين 0 و 1، مما يدل على احتمال تشغيل الوحدة المرئية أو إيقاف تشغيلها. هذا نموذج جيد للتعرف على الأحرف، حيث يكون الاهتمام على وحدات البكسل النشطة وأيها ليست كذلك. بالنسبة لصور المشاهد الطبيعية، لم يعد مناسبًا بسبب الخلفية والعمق وميل وحدات البكسل المجاورة إلى أخذ نفس القيم.
يتم إعطاء التوزيع الاحتمالي الشرطي لكل وحدة بواسطة دالة تنشيط السيني اللوجستي للمدخلات التي تتلقاها:
حيث \(\sigma\) هي دالة السيني اللوجستي:
2.9.1.3. تعلم أقصى احتمالية عشوائية#
تُعرف خوارزمية التدريب المُطبقة في BernoulliRBM باسم أقصى احتمالية عشوائية (SML) أو تباعد مُستمر مُتباين (PCD). تحسين أقصى احتمالية مُباشرةً أمر غير مُجدٍ بسبب شكل احتمالية البيانات:
من أجل التبسيط، تمت كتابة المعادلة أعلاه لمثال تدريب واحد. يتكون التدرج اللوني فيما يتعلق بالأوزان من مصطلحين يقابلان المصطلحين أعلاه. تُعرف عادةً باسم التدرج الإيجابي والتدرج السلبي، بسبب علاماتهما على التوالي. في هذا التطبيق، يتم تقدير التدرجات اللونية على دفعات صغيرة من العينات.
في تعظيم سجل الاحتمالية، يجعل التدرج الإيجابي النموذج يُفضّل الحالات المخفية التي تتوافق مع بيانات التدريب المُلاحظة. نظرًا للبنية ثنائية الأجزاء لـ RBMs، يمكن حسابها بكفاءة. ومع ذلك، فإن التدرج السلبي صعب المنال. هدفه هو تقليل طاقة الحالات المُشتركة التي يُفضّلها النموذج، وبالتالي جعله يظل صحيحًا للبيانات. يمكن تقريبه بواسطة سلسلة ماركوف مونتي كارلو باستخدام أخذ عينات جيبس الكتل عن طريق أخذ عينات بشكل مُتكرّر لكل من \(v\) و \(h\) بالنظر إلى الآخر، حتى تختلط السلسلة. تُسمى العينات التي تم إنشاؤها بهذه الطريقة أحيانًا جزيئات خيالية. هذا غير فعال ويصعب تحديد ما إذا كانت سلسلة ماركوف تختلط.
تقترح طريقة التباعد المُتباين إيقاف السلسلة بعد عدد صغير من التكرارات، \(k\)، عادةً حتى 1. هذه الطريقة سريعة ولها تباين منخفض، لكن العينات بعيدة عن توزيع النموذج.
يعالج التباعد المُستمر المُتباين هذا. بدلاً من بدء سلسلة جديدة في كل مرة تكون هناك حاجة إلى التدرج، وإجراء خطوة واحدة فقط من أخذ عينات جيبس، في PCD، نحتفظ بعدد من السلاسل (جزيئات خيالية) يتم تحديثها \(k\) خطوات جيبس بعد كل تحديث للوزن. هذا يسمح للجسيمات باستكشاف الفضاء بشكل أكثر شمولاً.
المراجع
"A fast learning algorithm for deep belief nets", G. Hinton, S. Osindero, Y.-W. Teh, 2006
"Training Restricted Boltzmann Machines using Approximations to the Likelihood Gradient", T. Tieleman, 2008
