1.3. انحدار حافة النواة

انحدار حافة النواة (KRR) [M2012] يجمع بين انحدار ريدج والتصنيف (المربعات الصغرى الخطية مع تنظيم قاعدة l2) مع خدعة النواة. وبالتالي يتعلم دالة خطية في الفضاء الناتج عن النواة المعنية والبيانات. لـ النوى غير الخطية، هذا يُقابل دالة غير خطية في الفضاء الأصلي.

شكل النموذج الذي تعلمه KernelRidge مطابق لانحدار متجه الدعم (SVR). ومع ذلك، يتم استخدام دوال خسارة مُختلفة: يستخدم KRR خسارة الخطأ التربيعي بينما يستخدم انحدار متجه الدعم خسارة \(\epsilon\) غير الحساسة، وكلاهما مُجتمع مع تنظيم l2. على عكس SVR، يمكن إجراء ملاءمة KernelRidge في شكل مُغلق وعادةً ما يكون أسرع بالنسبة لـ مجموعات البيانات متوسطة الحجم. من ناحية أخرى، فإن النموذج الذي تم تعلمه غير متفرق وبالتالي أبطأ من SVR، الذي يتعلم نموذجًا متفرقًا لـ \(\epsilon > 0\)، في وقت التنبؤ.

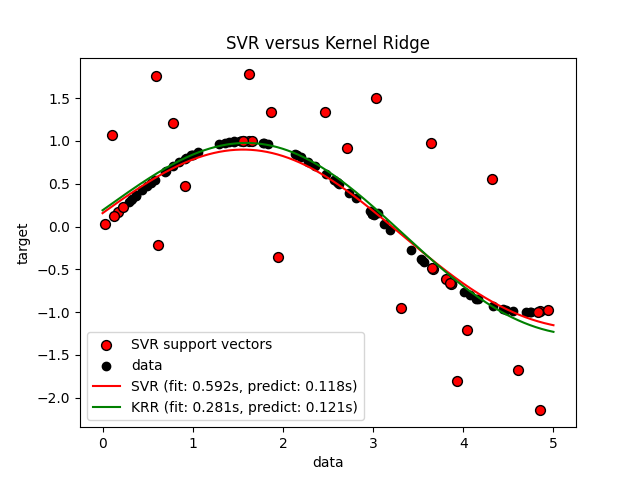
تُقارن الصورة التالية KernelRidge و SVR على مجموعة بيانات اصطناعية، تتكون من دالة هدف جيبية وضوضاء قوية تُضاف إلى كل نقطة بيانات خامسة. يتم رسم النموذج الذي تعلمه KernelRidge و SVR، حيث تم تحسين كل من التعقيد / التنظيم وعرض النطاق الترددي لنواة RBF باستخدام البحث الشبكي. الدوال التي تم تعلمها متشابهة جدًا؛ ومع ذلك، فإن ملاءمة KernelRidge أسرع بحوالي سبع مرات من ملاءمة SVR (كلاهما مع البحث الشبكي). ومع ذلك، فإن التنبؤ بـ 100000 قيمة هدف أسرع بأكثر من ثلاث مرات باستخدام SVR لأنه تعلم نموذجًا متفرقًا باستخدام 1/3 فقط تقريبًا من نقاط بيانات التدريب البالغ عددها 100 كمتجهات دعم.

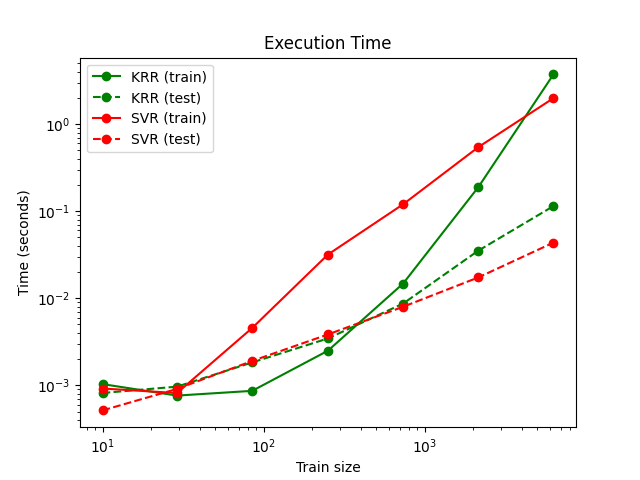
تُقارن الصورة التالية وقت ملاءمة وتنبؤ KernelRidge و SVR لأحجام مختلفة من مجموعة التدريب. ملاءمة KernelRidge أسرع من SVR لمجموعات التدريب متوسطة الحجم (أقل من 1000 عينة)؛ ومع ذلك، بالنسبة لمجموعات التدريب الأكبر، يتناسب SVR بشكل أفضل. فيما يتعلق بوقت التنبؤ، SVR أسرع من KernelRidge لجميع أحجام مجموعة التدريب بسبب الحل المتفرق الذي تم تعلمه. لاحظ أن درجة التفرق، وبالتالي وقت التنبؤ، يعتمد على المعلمتين \(\epsilon\) و \(C\) لـ SVR؛ \(\epsilon = 0\) سيُقابل نموذجًا كثيفًا.

أمثلة

• مقارنة بين الانحدار النووي المنتظم والانحدار الداعم للمتجهات

المراجع

[M2012]

"التعلم الآلي: منظور احتمالي" Murphy, K. P. - الفصل 14.4.3، الصفحات 492-493، The MIT Press، 2012