1.8. التحليل المتقاطع#
تحتوي وحدة التحليل المتقاطع على مقدرات خاضعة للإشراف لتقليل الأبعاد والانحدار، تنتمي إلى عائلة "المربعات الصغرى الجزئية".
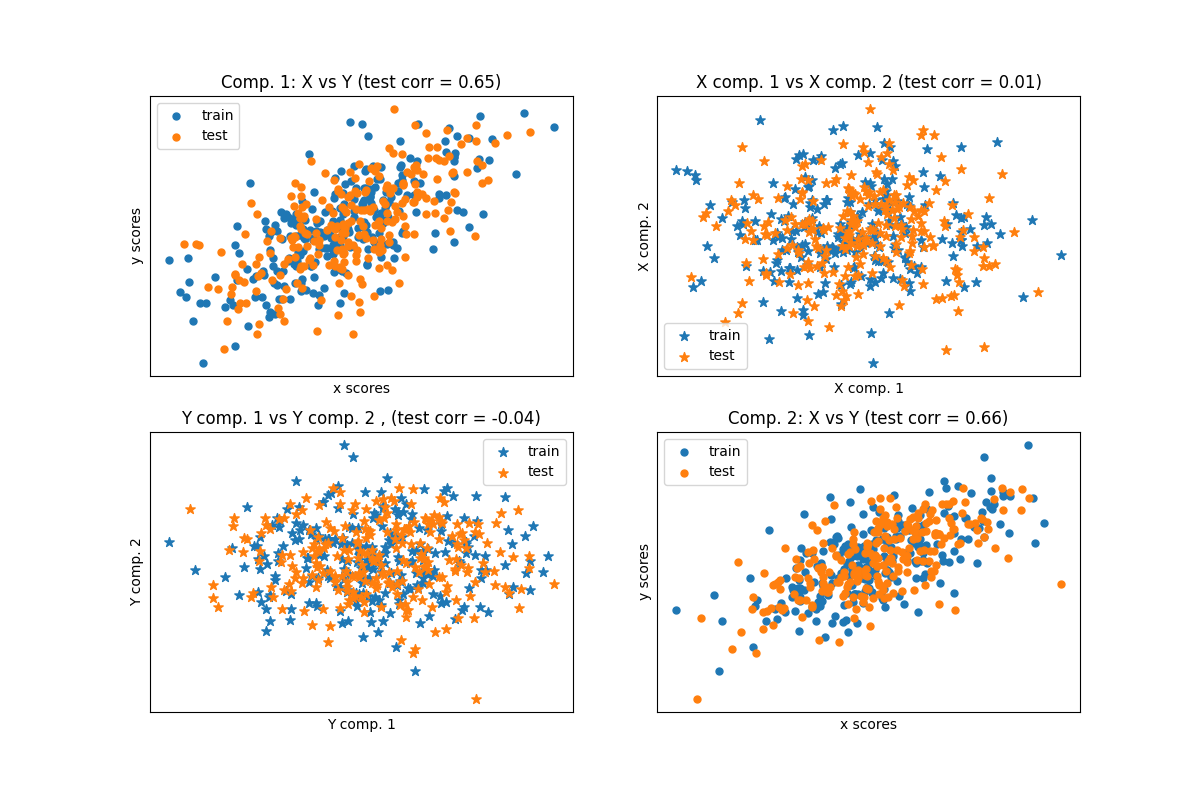
تجد خوارزميات التحليل المتقاطع العلاقات الأساسية بين مصفوفتين (X و Y).
إنها مناهج متغيرة كامنة لنمذجة هياكل التباين المشترك في هاتين المساحتين.
سيحاولون إيجاد الاتجاه متعدد الأبعاد في مساحة X الذي يفسر اتجاه التباين متعدد الأبعاد الأقصى في مساحة Y.
بمعنى آخر، يقوم PLS بإسقاط كل من X و Y في فضاء فرعي منخفض الأبعاد بحيث يكون التباين المشترك بين transformed(X) و transformed(Y) هو الحد الأقصى.
يرسم PLS أوجه تشابه مع Principal Component Regression (PCR)، حيث يتم أولاً إسقاط العينات في فضاء فرعي منخفض الأبعاد، ويتم توقع الأهداف y باستخدام transformed(X).
إحدى المشكلات المتعلقة بـ PCR هي أن تقليل الأبعاد غير خاضع للإشراف، وقد يفقد بعض المتغيرات المهمة: سيحتفظ PCR بالميزات ذات التباين الأكبر، ولكن من الممكن أن تكون الميزات ذات التباينات الصغيرة ذات صلة من التنبؤ بالهدف.
بطريقة ما، يسمح PLS بنفس النوع من تقليل الأبعاد، ولكن من خلال مراعاة الأهداف y.
يتم توضيح هذه الحقيقة في المثال التالي:
* sphx_glr_auto_examples_cross_decomposition/plot_pcr_vs_pls.py.
بصرف النظر عن CCA، فإن مقدرات PLS مناسبة بشكل خاص عندما تحتوي مصفوفة المتنبئين على متغيرات أكثر من الملاحظات، وعندما يكون هناك توافق متعدد بين الميزات. على النقيض من ذلك، سيفشل الانحدار الخطي القياسي في هذه الحالات ما لم يتم تنظيمه.
الفئات المضمنة في هذه الوحدة هي PLSRegression و PLSCanonical و CCA و PLSSVD
1.8.1. PLSCanonical#
نصف هنا الخوارزمية المستخدمة في PLSCanonical.
تستخدم المقدرات الأخرى متغيرات من هذه الخوارزمية، ويتم تفصيلها أدناه.
نوصي بالقسم [1] لمزيد من التفاصيل والمقارنات بين هذه الخوارزميات.
في [1]، يتوافق PLSCanonical مع "PLSW2A".
بالنظر إلى مصفوفتين متمركزتين \(X \in \mathbb{R}^{n \times d}\) و
\(Y \in \mathbb{R}^{n \times t}\)، وعدد من المكونات \(K\)،
PLSCanonical على النحو التالي:
عيّن \(X_1\) إلى \(X\) و \(Y_1\) إلى \(Y\). ثم، لكل \(k \in [1, K]\):
أ) احسب \(u_k \in \mathbb{R}^d\) و \(v_k \in \mathbb{R}^t\)، أول متجهات مفردة يسارية ويمنى لمصفوفة التباين المشترك \(C = X_k^T Y_k\). \(u_k\) و \(v_k\) تسمى الأوزان. بحكم التعريف، يتم اختيار \(u_k\) و \(v_k\) بحيث يزيدان من التباين المشترك بين \(X_k\) المسقط والهدف المسقط، أي \(\text{Cov}(X_k u_k,Y_k v_k)\).
ب) إسقاط \(X_k\) و \(Y_k\) على المتجهات المفردة للحصول على الدرجات: \(\xi_k = X_k u_k\) و \(\omega_k = Y_k v_k\)
ج) انحدار \(X_k\) على \(\xi_k\)، أي إيجاد متجه \(\gamma_k \in \mathbb{R}^d\) بحيث تكون مصفوفة الرتبة 1 \(\xi_k \gamma_k^T\) أقرب ما يمكن إلى \(X_k\). افعل الشيء نفسه على \(Y_k\) مع \(\omega_k\) للحصول على \(\delta_k\). المتجهات \(\gamma_k\) و \(\delta_k\) تسمى الأحمال.
د) إزالة \(X_k\) و \(Y_k\)، أي طرح الرتبة 1 التقريبات: \(X_{k+1} = X_k - \xi_k \gamma_k^T\)، و \(Y_{k + 1} = Y_k - \omega_k \delta_k^T\).
في النهاية، قمنا بتقريب \(X\) كمجموع مصفوفات الرتبة 1: \(X = \Xi \Gamma^T\) حيث \(\Xi \in \mathbb{R}^{n \times K}\) يحتوي على الدرجات في أعمدته، و \(\Gamma^T \in \mathbb{R}^{K\times d}\) يحتوي على الأحمال في صفوفه. وبالمثل بالنسبة لـ \(Y\)، لدينا \(Y = \Omega \Delta^T\).
لاحظ أن مصفوفات الدرجات \(\Xi\) و \(\Omega\) تتوافق مع إسقاطات بيانات التدريب \(X\) و \(Y\)، على التوالي.
يمكن تنفيذ الخطوة أ) بطريقتين: إما عن طريق حساب SVD الكامل لـ \(C\) والاحتفاظ فقط بالمتجهات المفردة ذات أكبر قيم مفردة، أو عن طريق حساب المتجهات المفردة مباشرةً باستخدام طريقة الطاقة (راجع القسم 11.3 في [1] )، والذي يتوافق مع خيار 'nipals' لمعلمة algorithm.
تحويل البيانات#
لتحويل \(X\) إلى \(\bar{X}\)، نحتاج إلى إيجاد مصفوفة إسقاط \(P\) بحيث تكون \(\bar{X} = XP\).
نعلم أنه بالنسبة لبيانات التدريب، \(\Xi = XP\)، و \(X = \Xi \Gamma^T\).
بتعيين \(P = U(\Gamma^T U)^{-1}\) حيث \(U\) هي المصفوفة مع \(u_k\) في الأعمدة، لدينا \(XP = X U(\Gamma^T U)^{-1} = \Xi (\Gamma^T U) (\Gamma^T U)^{-1} = \Xi\) كما هو مطلوب.
يمكن الوصول إلى مصفوفة الدوران \(P\) من سمة x_rotations_.
وبالمثل، يمكن تحويل \(Y\) باستخدام مصفوفة الدوران \(V(\Delta^T V)^{-1}\)، والتي يمكن الوصول إليها عبر سمة y_rotations_.
التنبؤ بالأهداف Y#
للتنبؤ بأهداف بعض البيانات \(X\)، نحن نبحث عن مصفوفة معامل \(\beta \in R^{d \times t}\) بحيث تكون \(Y =X\beta\).
الفكرة هي محاولة التنبؤ بالأهداف المحولة \(\Omega\) كدالة للعينات المحولة \(\Xi\)، عن طريق حساب \(\alpha \in \mathbb{R}\) بحيث تكون \(\Omega = \alpha \Xi\).
ثم، لدينا \(Y = \Omega \Delta^T = \alpha \Xi \Delta^T\)، وبما أن \(\Xi\) هي بيانات التدريب المحولة، لدينا \(Y = X \alpha P \Delta^T\)، ونتيجة لذلك مصفوفة المعامل \(\beta = \alpha P \Delta^T\).
يمكن الوصول إلى \(\beta\) من خلال سمة coef_.
1.8.2. PLSSVD#
PLSSVD هو إصدار مبسط من PLSCanonical الموصوف سابقًا: بدلاً من إزالة المصفوفات \(X_k\) و \(Y_k\) بشكل متكرر، يحسب PLSSVD SVD لـ \(C = X^TY\) مرة واحدة فقط، ويخزن n_components المتجهات المفردة المقابلة لأكبر القيم المفردة في المصفوفات U و V، المقابلة لسمات x_weights_ و y_weights_.
هنا، البيانات المحولة هي ببساطة transformed(X) = XU و transformed(Y) = YV.
إذا كان n_components == 1، فإن PLSSVD و PLSCanonical متكافئان تمامًا.
1.8.3. PLSRegression#
مقدر PLSRegression مشابه لـ PLSCanonical مع algorithm='nipals'، مع اختلافين مهمين:
في الخطوة أ) في طريقة الطاقة لحساب \(u_k\) و \(v_k\)، لا يتم تطبيع \(v_k\) أبدًا.
في الخطوة ج)، يتم تقريب الأهداف \(Y_k\) باستخدام إسقاط \(X_k\) (أي \(\xi_k\)) بدلاً من إسقاط \(Y_k\) (أي \(\omega_k\)). بمعنى آخر، يختلف حساب الأحمال. ونتيجة لذلك، سيتأثر الانكماش في الخطوة د) أيضًا.
يؤثر هذان التعديلان على ناتج predict و transform، وهما ليسا نفس ناتج PLSCanonical.
أيضًا، بينما يكون عدد المكونات محدودًا بـ min(n_samples, n_features, n_targets) في PLSCanonical، هنا يكون الحد هو رتبة \(X^TX\)، أي min(n_samples, n_features).
يُعرف PLSRegression أيضًا باسم PLS1 (أهداف فردية) و PLS2 (أهداف متعددة). مثل Lasso،
PLSRegression هو شكل من أشكال الانحدار الخطي المنتظم حيث يتحكم عدد المكونات في قوة التنظيم.
1.8.4. تحليل الارتباط المتعارف عليه#
تم تطوير تحليل الارتباط المتعارف عليه قبل PLS وبشكل مستقل.
لكن اتضح أن CCA هو حالة خاصة من PLS، ويتوافق مع PLS في "الوضع B" في الأدبيات.
يختلف CCA عن PLSCanonical في طريقة حساب الأوزان \(u_k\) و \(v_k\) في طريقة الطاقة للخطوة أ).
يمكن العثور على التفاصيل في القسم 10 من [1].
نظرًا لأن CCA يتضمن انعكاس \(X_k^TX_k\) و \(Y_k^TY_k\)، يمكن أن يكون هذا المقدر غير مستقر إذا كان عدد الميزات أو الأهداف أكبر من عدد العينات.
المراجع
أمثلة
sphx_glr_auto_examples_cross_decomposition/plot_compare_cross_decomposition.py
sphx_glr_auto_examples_cross_decomposition/plot_pcr_vs_pls.py
