2.5. تحليل الإشارات إلى مكونات (مشاكل تحليل المصفوفات)

2.5.1. تحليل المكونات الرئيسية (PCA)

2.5.1.1. PCA التحليل الأساسي الدقيق والتفسير الاحتمالي

يُستخدم PCA لتحليل مجموعة بيانات متعددة المتغيرات إلى مجموعة من المكونات المتعامدة المتتالية التي تُفسر أقصى قدر من التباين. في scikit-learn، يتم تنفيذ PCA ككائن مُحوِّل يتعلم \(n\) مكونات في أسلوبه fit، ويمكن استخدامه على بيانات جديدة لـ إسقاطها على هذه المكونات.

يُتمركز PCA ولكنه لا يُغيّر مقياس بيانات الإدخال لكل ميزة قبل تطبيق SVD. تُتيح المعلمة الاختيارية whiten=True إمكانية إسقاط البيانات على الفضاء الفردي مع تغيير مقياس كل مكون إلى تباين الوحدة. غالبًا ما يكون هذا مفيدًا إذا كانت النماذج في اتجاه مجرى النهر تضع افتراضات قوية على تجانس الخواص للإشارة: هذا هو الحال على سبيل المثال بالنسبة لآلات متجه الدعم مع نواة RBF وخوارزمية التجميع K-Means.

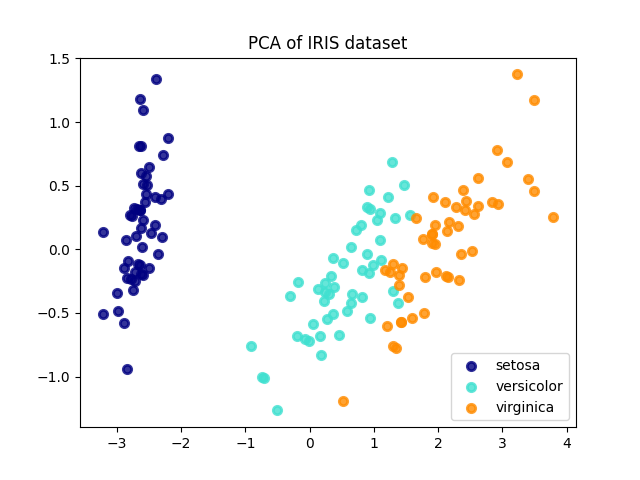
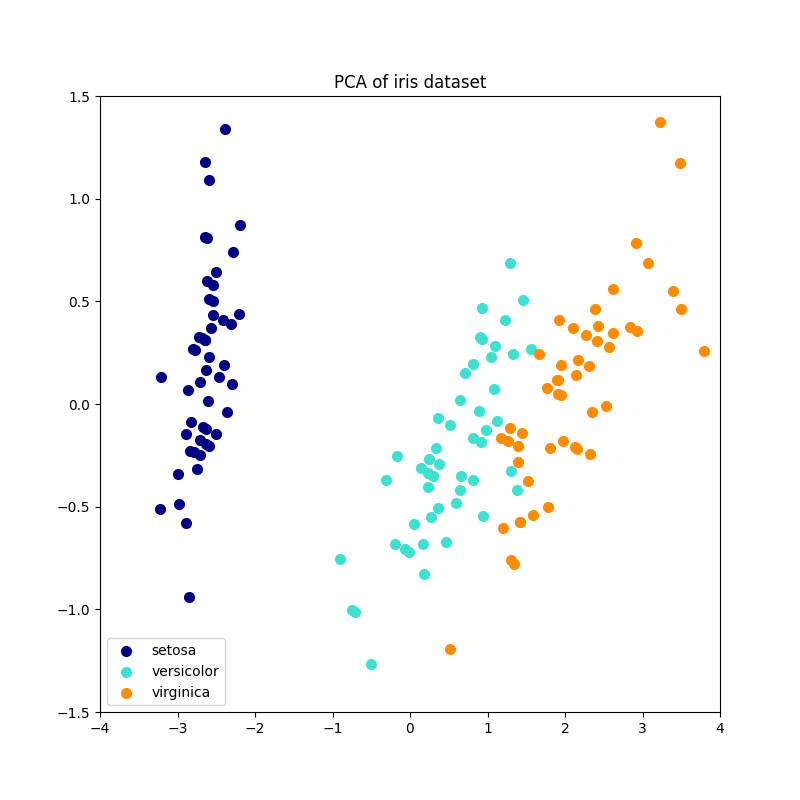
فيما يلي مثال على مجموعة بيانات iris، التي تتكون من 4 ميزات، مُسقطة على البُعدين اللذين يُفسران معظم التباين:

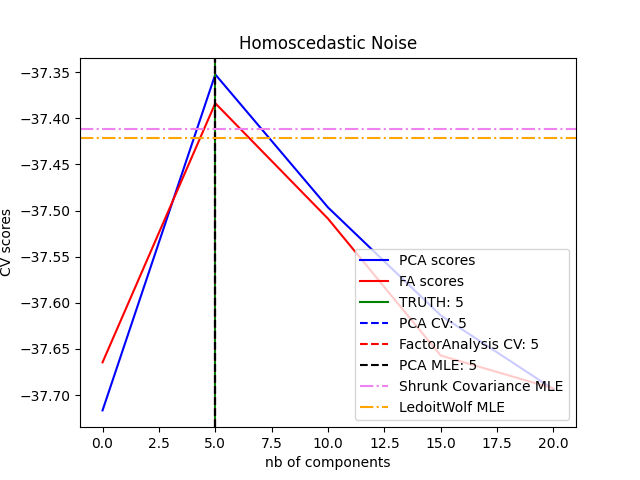
يُوفر كائن PCA أيضًا تفسيرًا احتماليًا لـ PCA يمكن أن يُعطي احتمالية للبيانات بناءً على مقدار التباين الذي تُفسره. على هذا النحو، فإنه يُطبق أسلوب score يمكن استخدامه في التحقق المتبادل:

أمثلة

• تحليل المكونات الرئيسية (PCA) على مجموعة بيانات Iris

• مقارنة بين الإسقاط ثنائي الأبعاد للمجموعة البيانات آيريس باستخدام LDA وPCA

• اختيار النموذج باستخدام التحليل الرئيسي للمكونات الاحتمالي وتحليل العوامل (FA)

2.5.1.2. Incremental PCA

كائن PCA مفيد جدًا، لكنه يحتوي على قيود مُعينة لـ مجموعات البيانات الكبيرة. القيد الأكبر هو أن PCA يدعم فقط المعالجة الدفعية، مما يعني أن جميع البيانات التي سيتم معالجتها يجب أن تتناسب مع الذاكرة الرئيسية. يستخدم كائن IncrementalPCA شكلًا مختلفًا من المعالجة ويسمح بحسابات جزئية تتطابق تقريبًا مع نتائج PCA أثناء معالجة البيانات بطريقة دفعية صغيرة. IncrementalPCA يُتيح تنفيذ تحليل المكونات الرئيسية خارج النواة إما عن طريق:

• استخدام أسلوبه partial_fit على أجزاء من البيانات التي تم جلبها بالتسلسل من القرص الصلب المحلي أو قاعدة بيانات الشبكة.

• استدعاء أسلوبه fit على ملف مُخصص للذاكرة باستخدام numpy.memmap.

IncrementalPCA يُخزِّن فقط تقديرات مكون وتباينات الضوضاء، من أجل تحديث explain_variance_ratio_ بشكل تدريجي. هذا هو السبب في أن استخدام الذاكرة يعتمد على عدد العينات لكل دفعة، بدلاً من عدد العينات التي سيتم معالجتها في مجموعة البيانات.

كما هو الحال في PCA، IncrementalPCA يُتمركز ولكنه لا يُغيّر مقياس بيانات الإدخال لكل ميزة قبل تطبيق SVD.

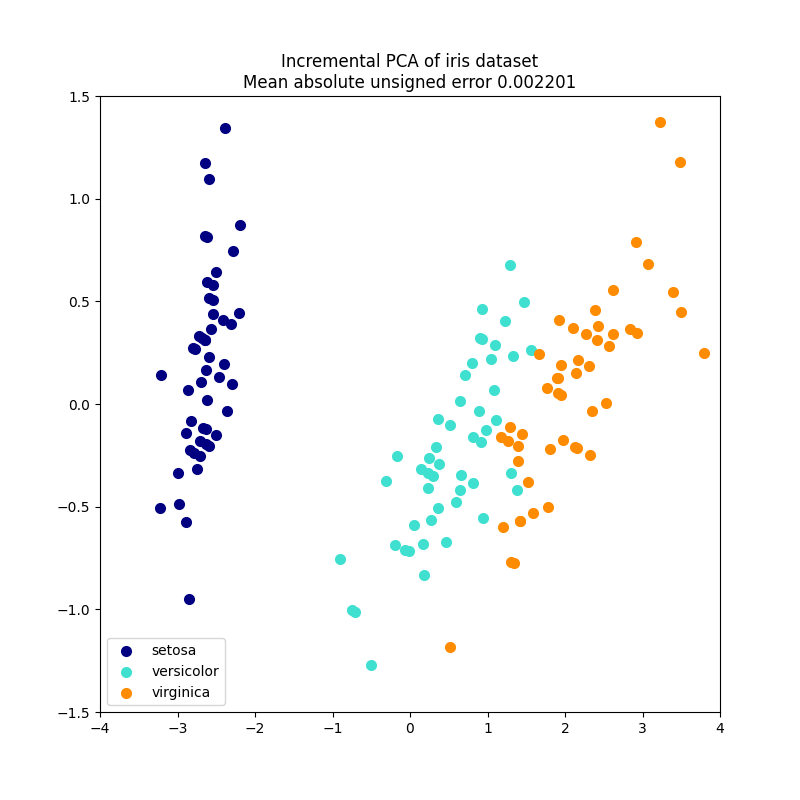
أمثلة

• sphx_glr_auto_examples_decomposition_plot_incremental_pca.py

2.5.1.3. PCA باستخدام SVD العشوائي

غالبًا ما يكون من المثير للاهتمام إسقاط البيانات على فضاء ذي أبعاد أقل يحافظ على معظم التباين، عن طريق إسقاط المتجه الفردي للمكونات المرتبطة بقيم فردية أقل.

على سبيل المثال، إذا كنا نعمل مع صور ذات مستوى رمادي 64x64 بكسل للتعرف على الوجه، فإن أبعاد البيانات هي 4096 ويكون تدريب آلة متجه دعم RBF على مثل هذه البيانات الواسعة بطيئًا. علاوة على ذلك، نحن نعلم أن أبعاد البيانات الجوهرية أقل بكثير من 4096 نظرًا لأن جميع صور الوجوه البشرية تبدو متشابهة إلى حد ما. تقع العينات على مُشعب ذي أبعاد أقل بكثير (على سبيل المثال حوالي 200). يمكن استخدام خوارزمية PCA لتحويل البيانات خطيًا مع تقليل الأبعاد والحفاظ على معظم التباين المُفسَّر في نفس الوقت.

فئة PCA المُستخدمة مع المعلمة الاختيارية svd_solver='randomized' مفيدة جدًا في هذه الحالة: نظرًا لأننا سنقوم بإسقاط معظم المتجهات الفردية، فمن الأكثر فعالية بكثير تقييد الحساب إلى تقدير تقريبي للمتجهات الفردية التي سنحتفظ بها لـ أداء التحويل فعليًا.

على سبيل المثال، يُظهر ما يلي 16 صورة شخصية عينة (مُتمركزة حول 0.0) من مجموعة بيانات Olivetti. على الجانب الأيمن توجد أول 16 متجهًا فرديًا أعيد تشكيلها كصور شخصية. نظرًا لأننا نطلب فقط أفضل 16 متجهًا فرديًا لمجموعة بيانات بحجم \(n_{samples} = 400\) و \(n_{features} = 64 \times 64 = 4096\)، فإن وقت الحساب أقل من 1 ثانية:

إذا لاحظنا \(n_{\max} = \max(n_{\mathrm{samples}}, n_{\mathrm{features}})\) و \(n_{\min} = \min(n_{\mathrm{samples}}, n_{\mathrm{features}})\)، فإن التعقيد الزمني لـ PCA العشوائي هو \(O(n_{\max}^2 \cdot n_{\mathrm{components}})\) بدلاً من \(O(n_{\max}^2 \cdot n_{\min})\) للأسلوب الدقيق المُطبق في PCA.

بصمة الذاكرة لـ PCA العشوائي تتناسب أيضًا مع \(2 \cdot n_{\max} \cdot n_{\mathrm{components}}\) بدلاً من \(n_{\max} \cdot n_{\min}\) للأسلوب الدقيق.

ملاحظة: تطبيق inverse_transform في PCA مع svd_solver='randomized' ليس التحويل العكسي الدقيق لـ transform حتى عندما يكون whiten=False (افتراضي).

أمثلة

• مثال على التعرف على الوجوه باستخدام الوجوه المميزة وآلات المتجهات الداعمة

• تحليلات مجموعة بيانات الوجوه

المراجع

• الخوارزمية 4.3 في "إيجاد الهيكل مع العشوائية: الخوارزميات العشوائية لـ بناء تحليلات مصفوفة تقريبية" Halko, et al., 2009

• "تطبيق خوارزمية عشوائية لتحليل المكونات الرئيسية" A. Szlam et al. 2014

2.5.1.4. تحليل المكونات الرئيسية المتفرقة (SparsePCA و MiniBatchSparsePCA)

SparsePCA هو متغير من PCA، بهدف استخراج مجموعة المكونات المتفرقة التي تُعيد بناء البيانات بشكل أفضل.

Mini-batch sparse PCA (MiniBatchSparsePCA) هو متغير من SparsePCA وهو أسرع ولكنه أقل دقة. يتم الوصول إلى السرعة المتزايدة عن طريق التكرار على أجزاء صغيرة من مجموعة الميزات، لعدد مُعين من التكرارات.

تحليل المكونات الرئيسية (PCA) له عيب أن المكونات التي يستخرجها هذا الأسلوب لها تعبيرات كثيفة حصريًا، أي لها معاملات غير صفرية عند التعبير عنها كمجموعات خطية من المتغيرات الأصلية. هذا يمكن أن يجعل التفسير صعبًا. في كثير من الحالات، يمكن تخيل المكونات الأساسية الحقيقية بشكل أكثر طبيعية كـ متجهات متفرقة؛ على سبيل المثال في التعرف على الوجه، قد تُعيَّن المكونات بشكل طبيعي لـ أجزاء من الوجوه.

تُنتج المكونات الرئيسية المتفرقة تمثيلًا أكثر اقتصادًا وقابلية للتفسير، مع التأكيد بوضوح على أي من الميزات الأصلية تُساهم في الاختلافات بين العينات.

يوضح المثال التالي 16 مكونًا تم استخراجها باستخدام PCA المتفرق من مجموعة بيانات وجوه Olivetti. يمكن ملاحظة كيف يُحفز مُصطلح التنظيم العديد من الأصفار. علاوة على ذلك، تتسبب البنية الطبيعية للبيانات في أن تكون المعاملات غير الصفرية متجاورة رأسيًا. لا يفرض النموذج هذا رياضيًا: كل مكون هو متجه \(h \in \mathbf{R}^{4096}\)، و لا يوجد مفهوم للتجاور الرأسي إلا أثناء التصور الصديق للإنسان كصور بكسل 64x64. حقيقة أن المكونات الموضحة أدناه تظهر محلية هي تأثير البنية الكامنة في البيانات، مما يجعل مثل هذه الأنماط المحلية تُقلل من خطأ إعادة البناء. توجد معايير مُحفزة للتفرق تأخذ في الاعتبار التجاور وأنواع مختلفة من الهياكل؛ راجع [Jen09] لمراجعة هذه الأساليب. لمزيد من التفاصيل حول كيفية استخدام Sparse PCA، راجع قسم الأمثلة، أدناه.

لاحظ أن هناك العديد من الصيغ المختلفة لمشكلة Sparse PCA. الصيغة المُطبقة هنا تستند إلى [Mrl09]. مشكلة التحسين التي تم حلها هي مشكلة PCA (تعلم القاموس) مع عقوبة \(\ell_1\) على المكونات:

\[\begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2} ||X-UV||_{\text{Fro}}^2+\alpha||V||_{1,1} \\ \text{subject to } & ||U_k||_2 <= 1 \text{ for all } 0 \leq k < n_{components}\end{split}\]

\(||.||_{\text{Fro}}\) تعني قاعدة Frobenius و \(||.||_{1,1}\) تعني قاعدة المصفوفة حسب الإدخال وهي مجموع القيم المطلقة لجميع الإدخالات في المصفوفة. تمنع قاعدة المصفوفة \(||.||_{1,1}\) المُحفزة للتفرق أيضًا تعلم المكونات من الضوضاء عند توفر عدد قليل من عينات التدريب. الدرجة من العقوبة (وبالتالي التفرق) يمكن تعديلها من خلال المعلمة الفائقة alpha. تؤدي القيم الصغيرة إلى تحليل مُنظَّم برفق، بينما تُقلِّص القيم الأكبر العديد من المعاملات إلى الصفر.

ملاحظة

بينما بروح خوارزمية على الإنترنت، فإن الفئة MiniBatchSparsePCA لا تُطبق partial_fit لأن الخوارزمية على الإنترنت على طول اتجاه الميزات، وليس اتجاه العينات.

أمثلة

• تحليلات مجموعة بيانات الوجوه

المراجع

[Mrl09]

"تعلم القاموس على الإنترنت للترميز المتفرق" J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009

[Jen09]

"تحليل المكونات الرئيسية المتفرقة المُهيكلة" R. Jenatton, G. Obozinski, F. Bach, 2009

2.5.2. تحليل المكونات الرئيسية للنواة (kPCA)

2.5.2.1. kPCA الدقيق

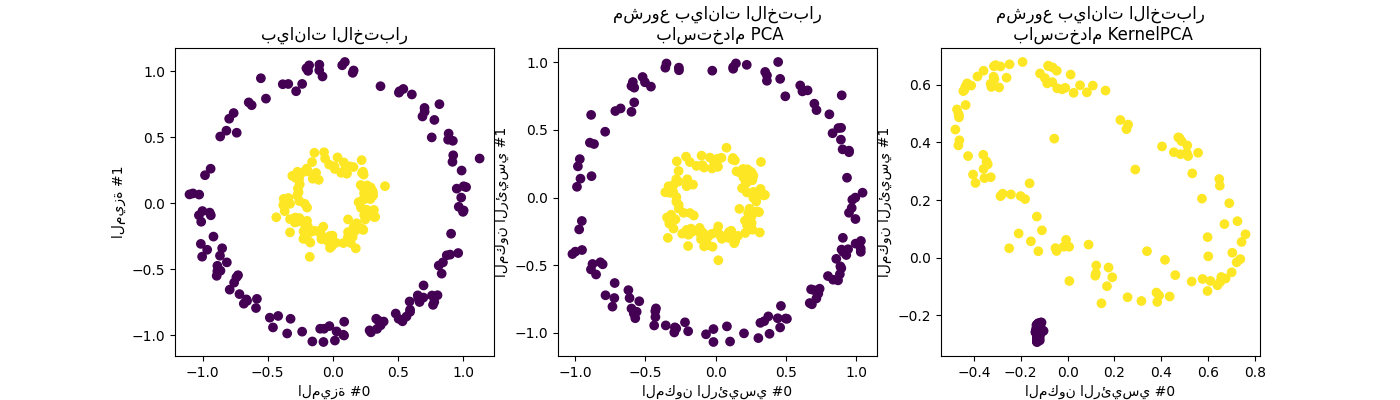
KernelPCA هو امتداد لـ PCA يحقق تقليلًا غير خطي للأبعاد من خلال استخدام النوى (انظر مقاييس المقارنة الزوجية، والصلات، والنوى (Kernels)) [Scholkopf1997]. لديها العديد من التطبيقات بما في ذلك إزالة الضوضاء والضغط والتنبؤ المُهيكل (تقدير تبعية النواة). KernelPCA يدعم كلاً من transform و inverse_transform.

ملاحظة

KernelPCA.inverse_transform يعتمد على حافة النواة لتعلم تعيين الدالة العينات من أساس PCA إلى مساحة الميزة الأصلية [Bakir2003]. وبالتالي، إعادة البناء التي تم الحصول عليها باستخدام KernelPCA.inverse_transform هي تقريبية. راجع المثال المرتبط أدناه لمزيد من التفاصيل.

أمثلة

• Kernel PCA

• إزالة التشويش من الصور باستخدام PCA النواة

المراجع

[Scholkopf1997]

Schölkopf, Bernhard, Alexander Smola, and Klaus-Robert Müller. "تحليل المكونات الرئيسية للنواة." المؤتمر الدولي حول الشبكات العصبية الاصطناعية. Springer, Berlin, Heidelberg, 1997.

[Bakir2003]

Bakır, Gökhan H., Jason Weston, and Bernhard Schölkopf. "التعلم لإيجاد صور مُسبقة." التقدم في أنظمة معالجة المعلومات العصبية 16 (2003): 449-456.

2.5.2.2. اختيار محلل لـ Kernel PCA

بينما في PCA يكون عدد المكونات مُحددًا بعدد الميزات، في KernelPCA يكون عدد المكونات مُحددًا بعدد العينات. تحتوي العديد من مجموعات البيانات في العالم الحقيقي على عدد كبير من العينات! في هذه الحالات، يكون إيجاد جميع المكونات باستخدام kPCA الكامل مضيعة لـ وقت الحساب، حيث يتم وصف البيانات في الغالب بواسطة المكونات القليلة الأولى (على سبيل المثال n_components<=100). بمعنى آخر، مصفوفة غرام المُتمركزة التي يتم تحليلها ذاتيًا في عملية ملاءمة Kernel PCA لها رتبة فعالة أصغر بكثير من حجمها. هذه حالة حيث يمكن أن تُوفر محللات القيم الذاتية التقريبية تسريعًا مع فقدان دقة منخفض جدًا.

محللات القيم الذاتية

يمكن استخدام المعلمة الاختيارية eigen_solver='randomized' لـ تقليل وقت الحساب بشكل كبير عندما يكون عدد n_components المطلوبة صغيرًا مُقارنةً بعدد العينات. يعتمد على أساليب التحليل العشوائي لإيجاد حل تقريبي في وقت أقصر.

التعقيد الزمني لـ KernelPCA العشوائي هو \(O(n_{\mathrm{samples}}^2 \cdot n_{\mathrm{components}})\) بدلاً من \(O(n_{\mathrm{samples}}^3)\) للأسلوب الدقيق المُطبق باستخدام eigen_solver='dense'.

تتناسب بصمة الذاكرة لـ KernelPCA العشوائي أيضًا مع \(2 \cdot n_{\mathrm{samples}} \cdot n_{\mathrm{components}}\) بدلاً من \(n_{\mathrm{samples}}^2\) للأسلوب الدقيق.

ملاحظة: هذه التقنية هي نفس التقنية المُستخدمة في PCA باستخدام SVD العشوائي.

بالإضافة إلى المحللين أعلاه، يمكن استخدام eigen_solver='arpack' كـ طريقة بديلة للحصول على تحليل تقريبي. من الناحية العملية، لا يُوفر هذا الأسلوب أوقات تنفيذ معقولة إلا عندما يكون عدد المكونات التي يجب إيجادها صغيرًا للغاية. يتم تمكينه افتراضيًا عندما يكون العدد المطلوب من المكونات أقل من 10 (بشكل صارم) ويكون عدد العينات أكثر من 200 (بشكل صارم). راجع KernelPCA للتفاصيل.

المراجع

• محلل dense: وثائق scipy.linalg.eigh

• محلل randomized:

  • الخوارزمية 4.3 في "إيجاد الهيكل مع العشوائية: الخوارزميات العشوائية لبناء تحليلات مصفوفة تقريبية" Halko, et al. (2009)

  • "تطبيق خوارزمية عشوائية لتحليل المكونات الرئيسية" A. Szlam et al. (2014)

• محلل arpack: وثائق scipy.sparse.linalg.eigsh R. B. Lehoucq, D. C. Sorensen, and C. Yang, (1998)

2.5.3. تحليل القيمة الفردية المقطوع والتحليل الدلالي الكامن

TruncatedSVD يُطبق متغيرًا من تحليل القيمة الفردية (SVD) الذي يحسب فقط أكبر \(k\) قيمة فردية، حيث \(k\) هي معلمة مُحددة من قبل المستخدم.

TruncatedSVD مُشابه جدًا لـ PCA، ولكنه يختلف في أن المصفوفة \(X\) لا تحتاج إلى أن تكون مُتمركزة. عندما يتم طرح متوسطات \(X\) حسب الأعمدة (لكل ميزة) من قيم الميزات، فإن SVD المقطوع على المصفوفة الناتجة يُعادل PCA.

حول SVD المقطوع والتحليل الدلالي الكامن (LSA)

عندما يتم تطبيق SVD المقطوع على مصفوفات مُصطلح-مستند (كما تم إرجاعها بواسطة CountVectorizer أو TfidfVectorizer)، يُعرف هذا التحويل باسم التحليل الدلالي الكامن (LSA)، لأنه يُحوِّل هذه المصفوفات إلى فضاء "دلالي" ذي أبعاد منخفضة. على وجه الخصوص، من المعروف أن LSA يُكافح آثار الترادف وتعدد المعاني (كلاهما يعني تقريبًا أن هناك معاني متعددة لكل كلمة)، مما يتسبب في أن تكون مصفوفات مُصطلح-مستند متفرقة بشكل مفرط وتُظهر تشابهًا ضعيفًا في ظل مقاييس مثل تشابه جيب التمام.

ملاحظة

يُعرف LSA أيضًا باسم الفهرسة الدلالية الكامنة، LSI، على الرغم من أن ذلك يشير بدقة إلى استخدامه في الفهارس الدائمة لأغراض استرجاع المعلومات.

رياضيًا، ينتج SVD المقطوع المُطبق على عينات التدريب \(X\) تقريبًا منخفض الرتبة \(X\):

\[X \approx X_k = U_k \Sigma_k V_k^\top\]

بعد هذه العملية، \(U_k \Sigma_k\) هي مجموعة التدريب المُحوَّلة بـ \(k\) ميزات (تُسمى n_components في API).

لتحويل مجموعة اختبار \(X\) أيضًا، نضربها في \(V_k\):

\[X' = X V_k\]

ملاحظة

معظم مُعالجات LSA في أدبيات مُعالجة اللغة الطبيعية (NLP) واسترجاع المعلومات (IR) تُبدِّل محاور المصفوفة \(X\) بحيث يكون لها شكل (n_features, n_samples). نُقدم LSA بطريقة مختلفة تتوافق مع واجهة برمجة تطبيقات scikit-learn بشكل أفضل، لكن القيم الفردية التي تم العثور عليها هي نفسها.

بينما يعمل مُحوِّل TruncatedSVD مع أي مصفوفة ميزات، يُوصى باستخدامه على مصفوفات tf-idf على حسابات التردد الأولية في إعداد LSA / مُعالجة المستندات. على وجه الخصوص، يجب تشغيل تغيير المقياس الفرعي وتردد المستند العكسي (sublinear_tf=True, use_idf=True) لتقريب قيم الميزات من التوزيع الغاوسي، للتعويض عن افتراضات LSA الخاطئة حول البيانات النصية.

أمثلة

• تجميع مستندات النص باستخدام k-means

المراجع

• Christopher D. Manning, Prabhakar Raghavan and Hinrich Schütze (2008), مقدمة في استرجاع المعلومات, Cambridge University Press, الفصل 18: تحليلات المصفوفة والفهرسة الدلالية الكامنة

2.5.4. تعلم القاموس

2.5.4.1. الترميز المتفرق بقاموس مُسبق الحساب

كائن SparseCoder هو مُقدِّر يمكن استخدامه لتحويل الإشارات إلى مجموعات خطية متفرقة من الذرات من قاموس ثابت مُسبق الحساب مثل أساس المويجات المنفصلة. لذلك لا يُطبق هذا الكائن أسلوب fit. يُعادل التحويل مشكلة ترميز متفرقة: إيجاد تمثيل للبيانات كمجموعة خطية من أقل عدد ممكن من ذرات القاموس. تُطبق جميع أشكال تعلم القاموس أساليب التحويل التالية، التي يمكن التحكم فيها عبر معلمة التهيئة transform_method:

• مطاردة التطابق المتعامد (مطاردة التطابق المتعامد (OMP))

• انحدار الزاوية الصغرى (انحدار الزاوية الصغرى)

• Lasso محسوب بواسطة انحدار الزاوية الصغرى

• Lasso باستخدام النزول الإحداثي (Lasso)

• تحديد العتبة

تحديد العتبة سريع جدًا ولكنه لا يُعطي عمليات إعادة بناء دقيقة. لقد ثبت أنها مفيدة في الأدبيات لمهام التصنيف. بالنسبة لمهام إعادة بناء الصور، تُعطي مطاردة التطابق المتعامد إعادة البناء الأكثر دقة وغير المُتحيزة.

تُوفر كائنات تعلم القاموس، عبر المعلمة split_code، إمكانية فصل القيم الموجبة والسالبة في نتائج الترميز المتفرق. هذا مفيد عندما يُستخدم تعلم القاموس لاستخراج الميزات التي سيتم استخدامها للتعلم الخاضع للإشراف، لأنه يسمح لـ خوارزمية التعلم بتعيين أوزان مختلفة للأحمال السالبة لـ ذرة مُعينة، من التحميل الموجب المُقابل.

كود التقسيم لعينة واحدة له طول 2 * n_components ويتم إنشاؤه باستخدام القاعدة التالية: أولاً، يتم حساب الكود العادي بطول n_components. ثم، يتم ملء أول n_components إدخال لـ split_code بجزء موجب من متجه الكود العادي. النصف الثاني من كود التقسيم ممتلئ بالجزء السالب من متجه الكود، فقط مع إشارة موجبة. لذلك، فإن split_code غير سالب.

أمثلة

• الترميز المتناثر مع قاموس محسوب مسبقًا

2.5.4.2. تعلم القاموس العام

تعلم القاموس (DictionaryLearning) هو مشكلة تحليل مصفوفة يُعادل إيجاد قاموس (عادةً ما يكون مكتملًا) سيؤدي أداءً جيدًا في الترميز المتفرق للبيانات المُناسبة.

تم اقتراح تمثيل البيانات كمجموعات متفرقة من الذرات من قاموس مكتمل ليكون الطريقة التي يعمل بها القشرة البصرية الأولية للثدييات. ونتيجة لذلك، فقد ثبت أن تعلم القاموس المُطبق على بقع الصور يُعطي نتائج جيدة في مهام معالجة الصور مثل إكمال الصور و الإصلاح وإزالة الضوضاء، وكذلك لمهام التعرف الخاضعة للإشراف.

تعلم القاموس هو مشكلة تحسين يتم حلها عن طريق التحديث بالتناوب للكود المتفرق، كحل لمشاكل Lasso متعددة، مع الأخذ في الاعتبار القاموس ثابتًا، ثم تحديث القاموس ليناسب الكود المتفرق بشكل أفضل.

\[\begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2} ||X-UV||_{\text{Fro}}^2+\alpha||U||_{1,1} \\ \text{subject to } & ||V_k||_2 <= 1 \text{ for all } 0 \leq k < n_{\mathrm{atoms}}\end{split}\]

\(||.||_{\text{Fro}}\) تعني قاعدة Frobenius و \(||.||_{1,1}\) تعني قاعدة المصفوفة حسب الإدخال وهي مجموع القيم المطلقة لجميع الإدخالات في المصفوفة. بعد استخدام هذا الإجراء لملاءمة القاموس، يكون التحويل ببساطة خطوة ترميز متفرقة تشترك في نفس التطبيق مع جميع كائنات تعلم القاموس (انظر الترميز المتفرق بقاموس مُسبق الحساب).

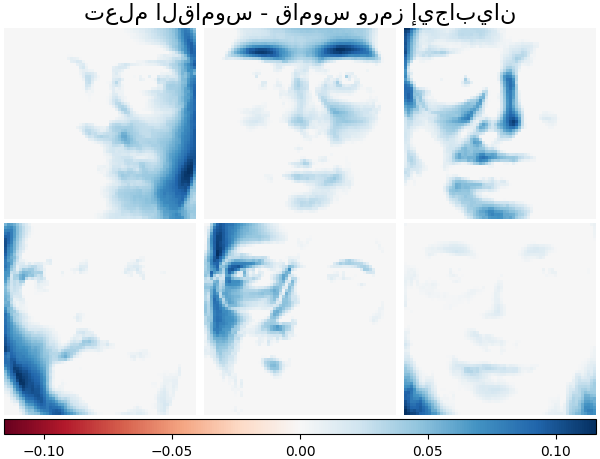
من الممكن أيضًا تقييد القاموس و / أو الكود ليكون موجبًا لـ مطابقة القيود التي قد تكون موجودة في البيانات. فيما يلي الوجوه مع قيود الإيجابية المختلفة المُطبقة. يشير اللون الأحمر إلى القيم السالبة، والأزرق يشير إلى القيم الموجبة، والأبيض يُمثِّل الأصفار.

تُظهر الصورة التالية كيف يبدو القاموس الذي تم تعلمه من بقع صور 4x4 بكسل مستخرجة من جزء من صورة وجه راكون.

أمثلة

• إزالة تشويش الصور باستخدام تعلم القاموس

المراجع

• "تعلم القاموس على الإنترنت للترميز المتفرق" J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009

2.5.4.3. تعلم القاموس الصغير الدفعي

MiniBatchDictionaryLearning يُطبق إصدارًا أسرع ولكنه أقل دقة لخوارزمية تعلم القاموس وهو أكثر ملاءمة لمجموعات البيانات الكبيرة.

افتراضيًا، MiniBatchDictionaryLearning يقسم البيانات إلى دفعات صغيرة ويُحسِّن نموذج NMF بطريقة على الإنترنت عن طريق التدوير على الدفعات الصغيرة لعدد التكرارات المُحدد. تتحكم معلمة batch_size في حجم الدفعات.

من أجل تسريع الخوارزمية الصغيرة الدفعية، من الممكن أيضًا تغيير مقياس الدفعات السابقة، مما يُعطيها أهمية أقل من الدفعات الأحدث. يتم ذلك عن طريق إدخال ما يسمى بعامل النسيان الذي تتحكم فيه معلمة forget_factor.

يُطبق المُقدِّر أيضًا partial_fit، الذي يُحدِّث H عن طريق التكرار مرة واحدة فقط على دفعة صغيرة. يمكن استخدام هذا للتعلم على الإنترنت عندما لا تكون البيانات متاحة بسهولة من البداية، أو عندما لا تتناسب البيانات مع الذاكرة.

التجميع لتعلم القاموس

لاحظ أنه عند استخدام تعلم القاموس لاستخراج تمثيل (على سبيل المثال للترميز المتفرق)، يمكن أن يكون التجميع بديلاً جيدًا لتعلم القاموس. على سبيل المثال، مُقدِّر MiniBatchKMeans فعال من الناحية الحسابية ويُطبق التعلم على الإنترنت باستخدام أسلوب partial_fit.

مثال: تعلم القاموس عبر الإنترنت لأجزاء الوجوه

2.5.5. تحليل العوامل

في التعلم غير الخاضع للإشراف، لدينا فقط مجموعة بيانات \(X = \{x_1, x_2, \dots, x_n \}\). كيف يمكن وصف مجموعة البيانات هذه رياضيًا؟ نموذج متغير كامن مُستمر بسيط جدًا لـ \(X\) هو

\[x_i = W h_i + \mu + \epsilon\]

يُسمى المتجه \(h_i\) "كامنًا" لأنه غير مُلاحظ. \(\epsilon\) يعتبر مُصطلح ضوضاء موزع وفقًا لتوزيع غاوسي بمتوسط 0 و تغاير مشترك \(\Psi\) (أي \(\epsilon \sim \mathcal{N}(0, \Psi)\)), \(\mu\) هو متجه إزاحة عشوائي. يُسمى هذا النموذج "تكويني" لأنه يصف كيف يتم إنشاء \(x_i\) من \(h_i\). إذا استخدمنا جميع \(x_i\) كأعمدة لتشكيل مصفوفة \(\mathbf{X}\) وجميع \(h_i\) كأعمدة لمصفوفة \(\mathbf{H}\) فيمكننا الكتابة (مع \(\mathbf{M}\) و \(\mathbf{E}\) مُحددين بشكل مناسب):

\[\mathbf{X} = W \mathbf{H} + \mathbf{M} + \mathbf{E}\]

بمعنى آخر، قمنا بتحليل المصفوفة \(\mathbf{X}\).

إذا تم إعطاء \(h_i\)، فإن المعادلة أعلاه تُشير تلقائيًا إلى التفسير الاحتمالي التالي:

\[p(x_i|h_i) = \mathcal{N}(Wh_i + \mu, \Psi)\]

بالنسبة لنموذج احتمالي كامل، نحتاج أيضًا إلى توزيع مُسبق لـ المتغير الكامن \(h\). الافتراض الأكثر وضوحًا (بناءً على الخصائص الجيدة لتوزيع غاوسي) هو \(h \sim \mathcal{N}(0, \mathbf{I})\). هذا يُعطي توزيع غاوسي كتوزيع هامشي لـ \(x\):

\[p(x) = \mathcal{N}(\mu, WW^T + \Psi)\]

الآن، بدون أي افتراضات أخرى، ستكون فكرة وجود متغير كامن \(h\) غير ضرورية - يمكن نمذجة \(x\) بالكامل بمتوسط وتغاير مشترك. نحتاج إلى فرض بعض الهياكل الأكثر تحديدًا على واحد من هاتين المعلمتين. افتراض إضافي بسيط يتعلق بـ هيكل تغاير الخطأ \(\Psi\):

• \(\Psi = \sigma^2 \mathbf{I}\): يؤدي هذا الافتراض إلى النموذج الاحتمالي لـ PCA.

• \(\Psi = \mathrm{diag}(\psi_1, \psi_2, \dots, \psi_n)\): يُسمى هذا النموذج FactorAnalysis، وهو نموذج إحصائي كلاسيكي. تُسمى المصفوفة W أحيانًا "مصفوفة تحميل العامل".

يُقدِّر كلا النموذجين بشكل أساسي توزيع غاوسي مع مصفوفة تغاير مشترك منخفضة الرتبة. نظرًا لأن كلا النموذجين احتماليان، فيمكن دمجهما في نماذج أكثر تعقيدًا، على سبيل المثال خليط من مُحللي العوامل. يحصل المرء على نماذج مُختلفة جدًا (على سبيل المثال FastICA) إذا تم افتراض توزيعات مُسبقة غير غاوسية على المتغيرات الكامنة.

يمكن لتحليل العوامل إنتاج مكونات مُشابهة (أعمدة مصفوفة التحميل الخاصة به) لـ PCA. ومع ذلك، لا يمكن للمرء إصدار أي بيانات عامة حول هذه المكونات (على سبيل المثال ما إذا كانت متعامدة):

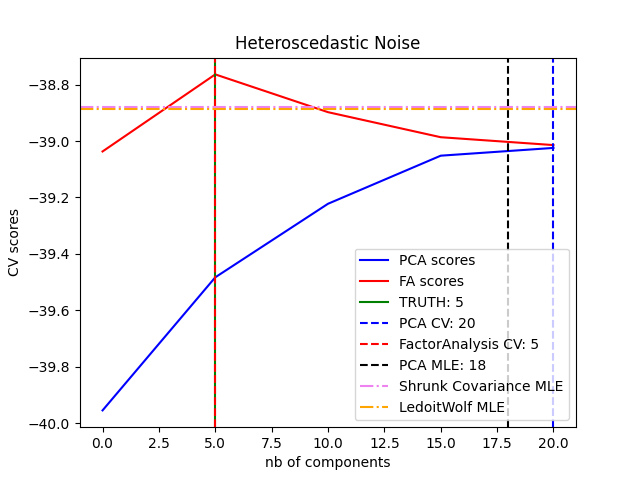
الميزة الرئيسية لتحليل العوامل على PCA هي أنه يمكنه نمذجة التباين في كل اتجاه من فضاء الإدخال بشكل مستقل (ضوضاء غير متجانسة):

هذا يسمح باختيار نموذج أفضل من PCA الاحتمالي في وجود ضوضاء غير متجانسة:

غالبًا ما يتبع تحليل العوامل دوران العوامل (مع المعلمة rotation)، عادةً لتحسين القابلية للتفسير. على سبيل المثال، يُعظِّم دوران Varimax مجموع تباينات الأحمال التربيعية، أي أنه يميل إلى إنتاج عوامل أكثر تفرقًا، والتي تتأثر ببضع ميزات فقط لكل منها ("الهيكل البسيط"). انظر على سبيل المثال المثال الأول أدناه.

أمثلة

• تحليل العوامل (مع الدوران) لتصور الأنماط

• اختيار النموذج باستخدام التحليل الرئيسي للمكونات الاحتمالي وتحليل العوامل (FA)

2.5.6. تحليل المكونات المستقلة (ICA)

يفصل تحليل المكونات المستقلة إشارة متعددة المتغيرات إلى مكونات فرعية مضافة مستقلة إلى أقصى حد. يتم تطبيقه في scikit-learn باستخدام خوارزمية Fast ICA. عادةً، لا يتم استخدام ICA لتقليل الأبعاد ولكن لفصل الإشارات المتراكبة. نظرًا لأن نموذج ICA لا يتضمن مُصطلح ضوضاء، لكي يكون النموذج صحيحًا، يجب تطبيق التبييض. يمكن القيام بذلك داخليًا باستخدام وسيطة whiten أو يدويًا باستخدام أحد متغيرات PCA.

يُستخدم بشكل كلاسيكي لفصل الإشارات المختلطة (مشكلة تُعرف باسم فصل المصدر الأعمى)، كما في المثال أدناه:

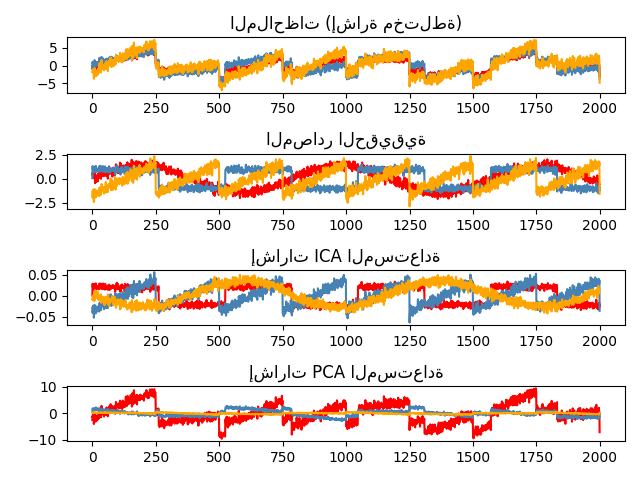
يمكن أيضًا استخدام ICA كتحليل غير خطي آخر يجد مكونات ذات بعض التفرق:

أمثلة

• فصل المصدر الأعمى باستخدام FastICA

• FastICA على سحب النقاط ثنائية الأبعاد

• تحليلات مجموعة بيانات الوجوه

2.5.7. تحليل المصفوفة غير السالبة (NMF أو NNMF)

2.5.7.1. NMF مع قاعدة Frobenius

NMF [1] هو نهج بديل للتحليل الذي يفترض أن البيانات والمكونات غير سالبة. يمكن توصيل NMF بدلاً من PCA أو متغيراته، في الحالات التي لا تحتوي فيها مصفوفة البيانات على قيم سالبة. يجد تحليلًا للعينات \(X\) إلى مصفوفتين \(W\) و \(H\) من العناصر غير السالبة، عن طريق تحسين المسافة \(d\) بين \(X\) وحاصل ضرب المصفوفة \(WH\). دالة المسافة الأكثر استخدامًا هي قاعدة Frobenius التربيعية، وهي امتداد واضح لقاعدة إقليدية للمصفوفات:

\[d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{\mathrm{Fro}}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2\]

على عكس PCA، يتم الحصول على تمثيل المتجه بطريقة مضافة، عن طريق تراكب المكونات، بدون طرح. هذه النماذج المضافة فعالة لتمثيل الصور والنصوص.

وقد لوحظ في [Hoyer, 2004] [2] أنه، عند تقييده بعناية، يمكن لـ NMF إنتاج تمثيل قائم على الأجزاء لمجموعة البيانات، مما يؤدي إلى نماذج قابلة للتفسير. يعرض المثال التالي 16 مكونًا متفرقًا عثر عليها NMF من الصور في مجموعة بيانات وجوه Olivetti، مُقارنةً بصور PCA الذاتية.

تحدد السمة init أسلوب التهيئة المُطبق، والذي له تأثير كبير على أداء الأسلوب. NMF يُطبق أسلوب تحليل القيمة الفردية المزدوج غير السالب. يعتمد NNDSVD [4] على عمليتي SVD، إحداهما تُقارب مصفوفة البيانات، والأخرى تُقارب أقسامًا موجبة من عوامل SVD الجزئية الناتجة باستخدام خاصية جبرية لمصفوفات الرتبة الوحدة. خوارزمية NNDSVD الأساسية مُناسبة بشكل أفضل لـ التحليل المتفرق. يُوصى بمتغيراتها NNDSVDa (حيث يتم تعيين جميع الأصفار على متوسط جميع عناصر البيانات)، و NNDSVDar (حيث يتم تعيين الأصفار إلى اضطرابات عشوائية أقل من متوسط البيانات مقسومًا على 100) في الحالة الكثيفة.

لاحظ أن محلل التحديث الضربي ('mu') لا يمكنه تحديث الأصفار الموجودة في التهيئة، لذلك يؤدي إلى نتائج أسوأ عند استخدامه مع خوارزمية NNDSVD الأساسية التي تُقدم الكثير من الأصفار؛ في هذه الحالة، يجب تفضيل NNDSVDa أو NNDSVDar.

يمكن أيضًا تهيئة NMF بمصفوفات عشوائية غير سالبة مُقيَّسة بشكل صحيح عن طريق تعيين init="random". يمكن أيضًا تمرير عدد صحيح أو RandomState إلى random_state للتحكم في إمكانية إعادة الإنتاج.

في NMF، يمكن إضافة مُسبقات L1 و L2 إلى دالة الخسارة من أجل تنظيم النموذج. يستخدم مُسبق L2 قاعدة Frobenius، بينما يستخدم مُسبق L1 قاعدة L1 حسب العنصر. كما هو الحال في ElasticNet، نتحكم في مزيج L1 و L2 باستخدام معلمة l1_ratio (\(\rho\))، وشدة التنظيم باستخدام معلمات alpha_W و alpha_H (\(\alpha_W\) و \(\alpha_H\)). يتم تغيير مقياس المُسبقات حسب عدد العينات (\(n\_samples\)) لـ H وعدد الميزات (\(n\_features\)) لـ W للحفاظ على تأثيرها متوازنًا مع بعضها البعض ومع مُصطلح ملاءمة البيانات مستقلًا قدر الإمكان عن حجم مجموعة التدريب. ثم مُصطلحات المُسبقات هي:

\[(\alpha_W \rho ||W||_1 + \frac{\alpha_W(1-\rho)}{2} ||W||_{\mathrm{Fro}} ^ 2) * n\_features + (\alpha_H \rho ||H||_1 + \frac{\alpha_H(1-\rho)}{2} ||H||_{\mathrm{Fro}} ^ 2) * n\_samples\]

ودالة الهدف المُنظَّمة هي:

\[d_{\mathrm{Fro}}(X, WH) + (\alpha_W \rho ||W||_1 + \frac{\alpha_W(1-\rho)}{2} ||W||_{\mathrm{Fro}} ^ 2) * n\_features + (\alpha_H \rho ||H||_1 + \frac{\alpha_H(1-\rho)}{2} ||H||_{\mathrm{Fro}} ^ 2) * n\_samples\]

2.5.7.2. NMF مع تباعد بيتا

كما هو موضح سابقًا، فإن دالة المسافة الأكثر استخدامًا هي قاعدة Frobenius التربيعية، وهي امتداد واضح لقاعدة إقليدية لـ المصفوفات:

\[d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{Fro}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2\]

يمكن استخدام دوال مسافة أخرى في NMF كما هو الحال، على سبيل المثال، تباعد Kullback-Leibler (KL) (المُعمم)، والذي يُشار إليه أيضًا باسم I-divergence:

\[d_{KL}(X, Y) = \sum_{i,j} (X_{ij} \log(\frac{X_{ij}}{Y_{ij}}) - X_{ij} + Y_{ij})\]

أو تباعد Itakura-Saito (IS):

\[d_{IS}(X, Y) = \sum_{i,j} (\frac{X_{ij}}{Y_{ij}} - \log(\frac{X_{ij}}{Y_{ij}}) - 1)\]

هذه المسافات الثلاث هي حالات خاصة لعائلة تباعد بيتا، مع \(\beta = 2, 1, 0\) على التوالي [6]. يتم تعريف تباعد بيتا بواسطة:

\[d_{\beta}(X, Y) = \sum_{i,j} \frac{1}{\beta(\beta - 1)}(X_{ij}^\beta + (\beta-1)Y_{ij}^\beta - \beta X_{ij} Y_{ij}^{\beta - 1})\]

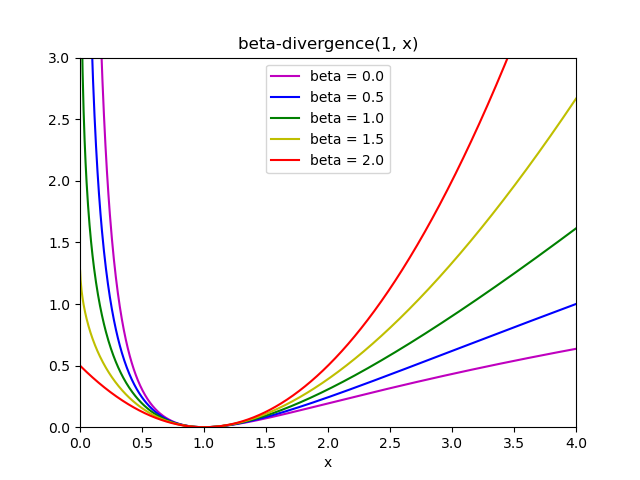
لاحظ أن هذا التعريف غير صالح إذا \(\beta \in (0; 1)\)، ومع ذلك يمكن تمديده باستمرار إلى تعريفات \(d_{KL}\) و \(d_{IS}\) على التوالي.

محللات NMF المُطبقة

NMF يُطبق محللين، باستخدام النزول الإحداثي ('cd') [5]، و التحديث الضربي ('mu') [6]. يمكن لمحلل 'mu' تحسين كل تباعد بيتا، بما في ذلك بالطبع قاعدة Frobenius (\(\beta=2\))، و تباعد Kullback-Leibler (المُعمم) (\(\beta=1\)) وتباعد Itakura-Saito (\(\beta=0\)). لاحظ أنه بالنسبة لـ \(\beta \in (1; 2)\)، يكون محلل 'mu' أسرع بكثير من قيم \(\beta\) الأخرى. لاحظ أيضًا أنه مع \(\beta\) سالبة (أو 0، أي 'itakura-saito')، لا يمكن أن تحتوي مصفوفة الإدخال على قيم صفرية.

يمكن لمحلل 'cd' تحسين قاعدة Frobenius فقط. نظرًا لـ عدم التحدب الكامن لـ NMF، قد تتقارب المحللات المختلفة إلى حدود دنيا مختلفة، حتى عند تحسين نفس دالة المسافة.

من الأفضل استخدام NMF مع أسلوب fit_transform، الذي يُعيد المصفوفة W. يتم تخزين المصفوفة H في النموذج المُناسب في الخاصية components_؛ سيقوم الأسلوب transform بتحليل مصفوفة جديدة X_new بناءً على هذه المكونات المخزنة:

>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]])
>>> from sklearn.decomposition import NMF
>>> model = NMF(n_components=2, init='random', random_state=0)
>>> W = model.fit_transform(X)
>>> H = model.components_
>>> X_new = np.array([[1, 0], [1, 6.1], [1, 0], [1, 4], [3.2, 1], [0, 4]])
>>> W_new = model.transform(X_new)

أمثلة

• تحليلات مجموعة بيانات الوجوه

• sphx_glr_auto_examples_applications_plot_topics_extraction_with_nmf_lda.py

2.5.7.3. تحليل المصفوفة غير السالبة الصغير الدفعي

MiniBatchNMF [7] يُطبق إصدارًا أسرع ولكنه أقل دقة لتحليل المصفوفة غير السالبة (أي NMF)، مُناسب بشكل أفضل لمجموعات البيانات الكبيرة.

افتراضيًا، MiniBatchNMF يقسم البيانات إلى دفعات صغيرة و يُحسِّن نموذج NMF بطريقة على الإنترنت عن طريق التدوير على الدفعات الصغيرة لعدد التكرارات المُحدد. تتحكم معلمة batch_size في حجم الدفعات.

من أجل تسريع الخوارزمية الصغيرة الدفعية، من الممكن أيضًا تغيير مقياس الدفعات السابقة، مما يُعطيها أهمية أقل من الدفعات الأحدث. يتم ذلك بإدخال ما يسمى بعامل النسيان الذي تتحكم فيه معلمة forget_factor.

يُطبق المُقدِّر أيضًا partial_fit، الذي يُحدِّث H عن طريق التكرار مرة واحدة فقط على دفعة صغيرة. يمكن استخدام هذا للتعلم على الإنترنت عندما لا تكون البيانات متاحة بسهولة من البداية، أو عندما لا تتناسب البيانات مع الذاكرة.

المراجع

[1]

"تعلم أجزاء الكائنات عن طريق تحليل المصفوفة غير السالبة" D. Lee, S. Seung, 1999

[2]

"تحليل المصفوفة غير السالبة مع قيود التفرق" P. Hoyer, 2004

[4]

"التهيئة القائمة على SVD: بداية جيدة لتحليل المصفوفة غير السالبة" C. Boutsidis, E. Gallopoulos, 2008

[5]

"خوارزميات محلية سريعة لتحليل المصفوفة والموتر غير السالب واسع النطاق." A. Cichocki, A. Phan, 2009

[6] (1,2)

"خوارزميات لتحليل المصفوفة غير السالبة مع تباعد بيتا" C. Fevotte, J. Idier, 2011

[7]

"خوارزميات على الإنترنت لتحليل المصفوفة غير السالبة مع تباعد Itakura-Saito" A. Lefevre, F. Bach, C. Fevotte, 2011

2.5.8. تخصيص ديريتشليت الكامن (LDA)

تخصيص ديريتشليت الكامن هو نموذج احتمالي تكويني لمجموعات مجموعات البيانات المنفصلة مثل مجموعات النصوص. وهو أيضًا نموذج موضوع يُستخدم لـ اكتشاف مواضيع مُجردة من مجموعة من المستندات.

النموذج الرسومي لـ LDA هو نموذج تكويني من ثلاثة مستويات:

ملاحظة حول الرموز المُقدمة في النموذج الرسومي أعلاه، والتي يمكن العثور عليها في Hoffman et al. (2013):

• المجموعة هي مجموعة من \(D\) مستندات.

• المستند هو تسلسل من \(N\) كلمات.

• هناك \(K\) مواضيع في المجموعة.

• تُمثِّل المربعات أخذ عينات متكرر.

في النموذج الرسومي، كل عقدة هي متغير عشوائي ولها دور في عملية التكوين. تشير العقدة المُظللة إلى متغير مُلاحظ وتشير العقدة غير المُظللة إلى متغير خفي (كامن). في هذه الحالة، الكلمات في المجموعة هي البيانات الوحيدة التي نُلاحظها. تحدد المتغيرات الكامنة الخليط العشوائي للمواضيع في المجموعة وتوزيع الكلمات في المستندات. الهدف من LDA هو استخدام الكلمات المُلاحظة للاستدلال على هيكل الموضوع الخفي.

تفاصيل حول نمذجة مجموعات النصوص

عند نمذجة مجموعات النصوص، يفترض النموذج عملية التكوين التالية لمجموعة تحتوي على \(D\) مستندات و \(K\) مواضيع، مع \(K\) مُقابلة لـ n_components في API:

1. لكل موضوع \(k \in K\)، ارسم \(\beta_k \sim \mathrm{Dirichlet}(\eta)\). هذا يُوفر توزيعًا على الكلمات، أي احتمال ظهور كلمة في الموضوع \(k\). \(\eta\) تقابل topic_word_prior.

2. لكل مستند \(d \in D\)، ارسم نسب الموضوع \(\theta_d \sim \mathrm{Dirichlet}(\alpha)\). \(\alpha\) تقابل doc_topic_prior.

3. لكل كلمة \(i\) في المستند \(d\):

   1. ارسم تعيين الموضوع \(z_{di} \sim \mathrm{Multinomial} (\theta_d)\)

   2. ارسم الكلمة المُلاحظة \(w_{ij} \sim \mathrm{Multinomial} (\beta_{z_{di}})\)

لتقدير المعلمات، التوزيع اللاحق هو:

\[p(z, \theta, \beta |w, \alpha, \eta) = \frac{p(z, \theta, \beta|\alpha, \eta)}{p(w|\alpha, \eta)}\]

نظرًا لأن التوزيع اللاحق صعب التعامل معه، فإن أسلوب بايز المتغير يستخدم توزيعًا أبسط \(q(z,\theta,\beta | \lambda, \phi, \gamma)\) لتقريبه، ويتم تحسين معلمات التباين هذه \(\lambda\) و \(\phi\) و \(\gamma\) لزيادة الحد الأدنى للأدلة (ELBO):

\[\log\: P(w | \alpha, \eta) \geq L(w,\phi,\gamma,\lambda) \overset{\triangle}{=} E_{q}[\log\:p(w,z,\theta,\beta|\alpha,\eta)] - E_{q}[\log\:q(z, \theta, \beta)]\]

زيادة ELBO يُعادل تقليل تباعد Kullback-Leibler (KL) بين \(q(z,\theta,\beta)\) والتوزيع اللاحق الحقيقي \(p(z, \theta, \beta |w, \alpha, \eta)\).

LatentDirichletAllocation يُطبق خوارزمية بايز المتغيرة على الإنترنت و يدعم كل من أساليب التحديث على الإنترنت والدفعية. بينما يُحدِّث الأسلوب الدفعي متغيرات التباين بعد كل تمريرة كاملة عبر البيانات، يُحدِّث الأسلوب على الإنترنت متغيرات التباين من نقاط بيانات الدفعة الصغيرة.

ملاحظة

على الرغم من أن الأسلوب على الإنترنت مُضمَّن للتقارب إلى نقطة مثلى محليًا، إلا أن جودة النقطة المثلى وسرعة التقارب قد تعتمد على حجم الدفعة الصغيرة و السمات المتعلقة بإعداد مُعدل التعلم.

عندما يتم تطبيق LatentDirichletAllocation على مصفوفة "مصطلح-مستند"، سيتم تحليل المصفوفة إلى مصفوفة "موضوع-مصطلح" ومصفوفة "مستند-موضوع". بينما يتم تخزين مصفوفة "موضوع-مصطلح" كـ components_ في النموذج، يمكن حساب مصفوفة "مستند-موضوع" من أسلوب transform.

LatentDirichletAllocation يُطبق أيضًا أسلوب partial_fit. يُستخدم هذا عندما يمكن جلب البيانات بالتسلسل.

أمثلة

• sphx_glr_auto_examples_applications_plot_topics_extraction_with_nmf_lda.py

المراجع

• "تخصيص ديريتشليت الكامن" D. Blei, A. Ng, M. Jordan, 2003

• "التعلم على الإنترنت لتخصيص ديريتشليت الكامن” M. Hoffman, D. Blei, F. Bach, 2010

• "الاستدلال العشوائي المتغير" M. Hoffman, D. Blei, C. Wang, J. Paisley, 2013

• "معيار varimax للدوران التحليلي في تحليل العوامل" H. F. Kaiser, 1958

انظر أيضًا تخفيض الأبعاد لتقليل الأبعاد باستخدام تحليل مكونات الجوار.