2.8. تقدير الكثافة

يتنقل تقدير الكثافة بين التعلم غير الخاضع للإشراف وهندسة الميزات ونمذجة البيانات. بعض تقنيات تقدير الكثافة الأكثر شيوعًا وفائدة هي نماذج الخليط مثل خليط غاوسي (GaussianMixture)، و الأساليب القائمة على الجوار مثل تقدير كثافة النواة (KernelDensity). تتم مناقشة خليط غاوسي بشكل كامل في سياق التجميع، لأن هذه التقنية مفيدة أيضًا كـ مخطط تجميع غير خاضع للإشراف.

تقدير الكثافة هو مفهوم بسيط للغاية، ومعظم الناس على دراية بالفعل بتقنية تقدير كثافة شائعة: الرسم البياني.

2.8.1. تقدير الكثافة: الرسوم البيانية

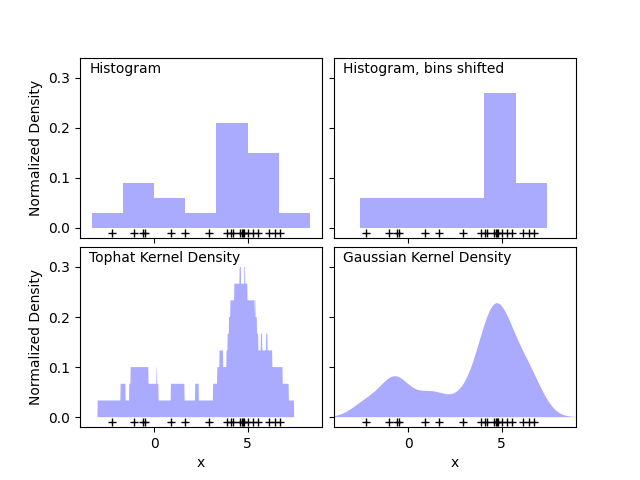
الرسم البياني هو تصور بسيط للبيانات حيث يتم تحديد الصناديق، و يتم حساب عدد نقاط البيانات داخل كل صندوق. مثال على الرسم البياني يمكن رؤيته في اللوحة العلوية اليسرى من الشكل التالي:

ومع ذلك، فإن مشكلة رئيسية في الرسوم البيانية هي أن اختيار الصناديق يمكن أن يكون له تأثير غير متناسب على التصور الناتج. خذ بعين الاعتبار اللوحة العلوية اليمنى من الشكل أعلاه. تُظهر رسمًا بيانيًا على نفس البيانات، مع إزاحة الصناديق إلى اليمين. تبدو نتائج التصورين مختلفة تمامًا، وقد تؤدي إلى تفسيرات مختلفة للبيانات.

بشكل حدسي، يمكن للمرء أيضًا التفكير في الرسم البياني على أنه كومة من الكتل، كتلة واحدة لكل نقطة. عن طريق تكديس الكتل في مساحة الشبكة المناسبة، نستعيد الرسم البياني. ولكن ماذا لو، بدلاً من تكديس الكتل على شبكة منتظمة، قمنا بوضع كل كتلة في مركز النقطة التي تُمثلها، وجمعنا الارتفاع الإجمالي في كل موقع؟ تؤدي هذه الفكرة إلى التصور السفلي الأيسر. ربما ليس بنفس نقاء الرسم البياني، لكن حقيقة أن البيانات تقود مواقع الكتل تعني أنها تمثيل أفضل بكثير للبيانات الأساسية.

هذا التصور هو مثال على تقدير كثافة النواة، في هذه الحالة مع نواة قبعة علوية (أي كتلة مربعة عند كل نقطة). يمكننا استعادة توزيع أكثر سلاسة باستخدام نواة أكثر سلاسة. يُظهر الرسم البياني السفلي الأيمن تقدير كثافة نواة غاوسي، حيث تُساهم كل نقطة بمنحنى غاوسي إلى الإجمالي. والنتيجة هي تقدير كثافة سلس مُشتق من البيانات، ويعمل كنموذج غير معلمي قوي لـ توزيع النقاط.

2.8.2. تقدير كثافة النواة

يتم تنفيذ تقدير كثافة النواة في scikit-learn في مُقدِّر KernelDensity، الذي يستخدم شجرة الكرة أو شجرة KD للاستعلامات الفعالة (انظر أقرب الجيران لـ مناقشة هذه). على الرغم من أن المثال أعلاه يستخدم مجموعة بيانات أحادية الأبعاد من أجل البساطة، إلا أنه يمكن إجراء تقدير كثافة النواة في أي عدد من الأبعاد، على الرغم من أن لعنة الأبعاد في الممارسة العملية تتسبب في تدهور أدائها في الأبعاد العالية.

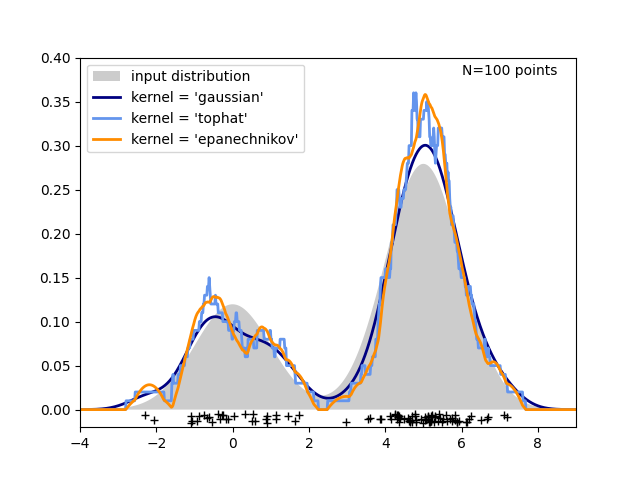
في الشكل التالي، يتم رسم 100 نقطة من توزيع ثنائي النسق، ويتم عرض تقديرات كثافة النواة لثلاثة اختيارات من النوى:

من الواضح كيف يؤثر شكل النواة على سلاسة التوزيع الناتج. يمكن استخدام مُقدِّر كثافة النواة scikit-learn على النحو التالي:

>>> from sklearn.neighbors import KernelDensity
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
>>> kde.score_samples(X)
array([-0.41075698, -0.41075698, -0.41076071, -0.41075698, -0.41075698,
       -0.41076071])

هنا استخدمنا kernel='gaussian'، كما رأينا أعلاه. رياضيًا، النواة هي دالة موجبة \(K(x;h)\) التي يتم التحكم فيها بواسطة معلمة عرض النطاق \(h\). بالنظر إلى شكل النواة هذا، يتم إعطاء تقدير الكثافة عند نقطة \(y\) داخل مجموعة من النقاط \(x_i; i=1\cdots N\) بواسطة:

\[\rho_K(y) = \sum_{i=1}^{N} K(y - x_i; h)\]

يعمل عرض النطاق هنا كمعلمة تنعيم، ويتحكم في المفاضلة بين التحيز والتباين في النتيجة. يؤدي عرض النطاق الترددي الكبير إلى توزيع كثافة سلس للغاية (أي تحيز عالي). يؤدي عرض النطاق الترددي الصغير إلى توزيع كثافة غير سلس (أي تباين عالي).

تتحكم المعلمة bandwidth في هذا التنعيم. يمكن للمرء إما تعيين هذه المعلمة يدويًا أو استخدام أساليب تقدير Scott و Silvermann.

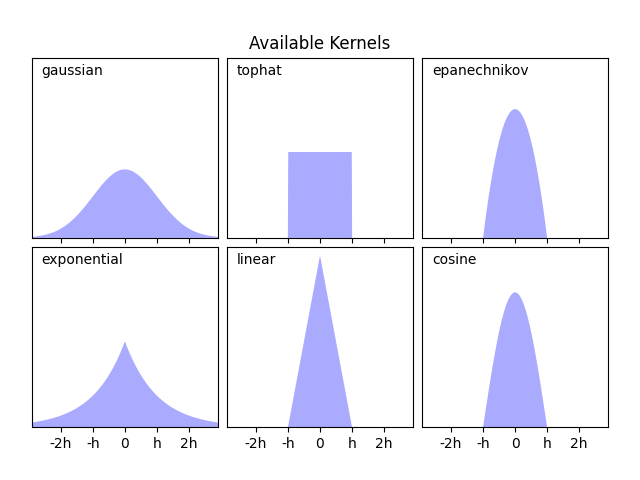
KernelDensity يُطبق العديد من أشكال النواة الشائعة، والتي تظهر في الشكل التالي:

التعبيرات الرياضية للنوى

شكل هذه النوى هو كما يلي:

• نواة غاوسي (kernel = 'gaussian')

  \(K(x; h) \propto \exp(- \frac{x^2}{2h^2} )\)

• نواة قبعة علوية (kernel = 'tophat')

  \(K(x; h) \propto 1\) إذا \(x < h\)

• نواة Epanechnikov (kernel = 'epanechnikov')

  \(K(x; h) \propto 1 - \frac{x^2}{h^2}\)

• نواة أسية (kernel = 'exponential')

  \(K(x; h) \propto \exp(-x/h)\)

• نواة خطية (kernel = 'linear')

  \(K(x; h) \propto 1 - x/h\) إذا \(x < h\)

• نواة جيب التمام (kernel = 'cosine')

  \(K(x; h) \propto \cos(\frac{\pi x}{2h})\) إذا \(x < h\)

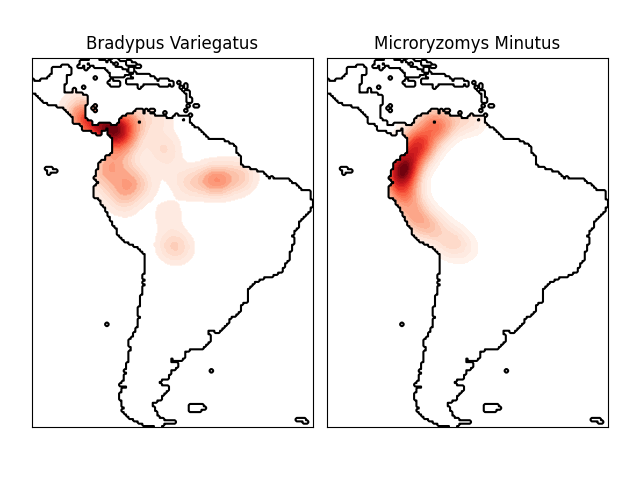
يمكن استخدام مُقدِّر كثافة النواة مع أي من مقاييس المسافة الصالحة (انظر DistanceMetric للحصول على قائمة بالمقاييس المتاحة)، على الرغم من أن النتائج مُطبَّعة بشكل صحيح فقط لمقياس إقليدية. مقياس مفيد بشكل خاص هو مسافة Haversine التي تقيس المسافة الزاوية بين النقاط على كرة. هنا مثال على استخدام تقدير كثافة النواة لتصور البيانات الجغرافية المكانية، في هذه الحالة توزيع ملاحظات اثنين من الأنواع المختلفة في قارة أمريكا الجنوبية:

تطبيق آخر مفيد لتقدير كثافة النواة هو تعلم نموذج تكويني غير معلمي لمجموعة بيانات من أجل رسم عينات جديدة بكفاءة من هذا النموذج التكويني. فيما يلي مثال على استخدام هذه العملية لـ إنشاء مجموعة جديدة من الأرقام المكتوبة بخط اليد، باستخدام نواة غاوسي تم تعلمها على إسقاط PCA للبيانات:

تتكون البيانات "الجديدة" من مجموعات خطية من بيانات الإدخال، مع أوزان مرسومة احتماليًا بالنظر إلى نموذج KDE.

أمثلة

• تقدير كثافة النواة البسيطة أحادية البعد: حساب تقديرات كثافة النواة البسيطة في بُعد واحد.

• تقدير كثافة النواة: مثال على استخدام تقدير كثافة النواة لتعلم نموذج تكويني لبيانات الأرقام المكتوبة بخط اليد، ورسم عينات جديدة من هذا النموذج.

• تقدير كثافة النواة لتوزيع الأنواع: مثال على تقدير كثافة النواة باستخدام مقياس مسافة Haversine لتصور البيانات الجغرافية المكانية