6.7. Kernel Approximation

تحتوي هذه الوحدة الفرعية على دوال تُقارب تعيينات الميزات التي تُقابل نوى مُعينة، كما تُستخدم على سبيل المثال في آلات متجه الدعم (انظر آلات الدعم المتجهية (SVM)). تُجري دوال الميزات التالية تحويلات غير خطية لـ الإدخال، والتي يمكن أن تُخدِّم كأساس للتصنيف الخطي أو الخوارزميات الأخرى.

ميزة استخدام تعيينات الميزات الصريحة التقريبية مُقارنةً بـ خدعة النواة، التي تستخدم تعيينات الميزات ضمنيًا، هي أن التعيينات الصريحة يمكن أن تكون أكثر ملاءمة للتعلم على الإنترنت ويمكن أن تُقلل بشكل كبير من تكلفة التعلم مع مجموعات البيانات الكبيرة جدًا. لا تتناسب SVMs القياسية المُستخدمة للنواة بشكل جيد مع مجموعات البيانات الكبيرة، ولكن باستخدام تعيين نواة تقريبي، من الممكن استخدام SVMs خطية أكثر كفاءة. على وجه الخصوص، يمكن لمزيج من تقديرات تعيين النواة مع SGDClassifier جعل التعلم غير الخطي على مجموعات البيانات الكبيرة مُمكناً.

نظرًا لعدم وجود الكثير من العمل التجريبي باستخدام عمليات التضمين التقريبية، فمن المستحسن مقارنة النتائج مع أساليب النواة الدقيقة عندما يكون ذلك مُمكناً.

شاهد أيضا

الانحدار متعدد الحدود: توسيع النماذج الخطية مع دوال الأساس لتحويل متعدد الحدود دقيق.

6.7.1. أسلوب Nystroem لتقريب النواة

أسلوب Nystroem، كما هو مُطبق في Nystroem، هو أسلوب عام لـ تقريب النوى منخفضة الرتبة. إنه يُحقق ذلك عن طريق أخذ عينات فرعية بدون استبدال صفوف / أعمدة البيانات التي يتم تقييم النواة عليها. بينما التعقيد الحسابي للأسلوب الدقيق هو \(\mathcal{O}(n^3_{\text{samples}})\)، فإن تعقيد التقريب هو \(\mathcal{O}(n^2_{\text{components}} \cdot n_{\text{samples}})\)، حيث يمكن للمرء تعيين \(n_{\text{components}} \ll n_{\text{samples}}\) بدون انخفاض كبير في الأداء [WS2001].

يمكننا بناء التحليل الذاتي لمصفوفة النواة \(K\)، بناءً على ميزات البيانات، ثم تقسيمها إلى نقاط بيانات تم أخذ عينات منها ونقاط بيانات لم يتم أخذ عينات منها.

\[\begin{split}K = U \Lambda U^T = \begin{bmatrix} U_1 \\ U_2\end{bmatrix} \Lambda \begin{bmatrix} U_1 \\ U_2 \end{bmatrix}^T = \begin{bmatrix} U_1 \Lambda U_1^T & U_1 \Lambda U_2^T \\ U_2 \Lambda U_1^T & U_2 \Lambda U_2^T \end{bmatrix} \equiv \begin{bmatrix} K_{11} & K_{12} \\ K_{21} & K_{22} \end{bmatrix}\end{split}\]

حيث:

• \(U\) متعامدة

• \(\Lambda\) مصفوفة قطرية من القيم الذاتية

• \(U_1\) مصفوفة متعامدة من العينات التي تم اختيارها

• \(U_2\) مصفوفة متعامدة من العينات التي لم يتم اختيارها

بالنظر إلى أنه يمكن الحصول على \(U_1 \Lambda U_1^T\) عن طريق تعامد المصفوفة \(K_{11}\)، ويمكن تقييم \(U_2 \Lambda U_1^T\) (وكذلك مدورها)، فإن المصطلح الوحيد المتبقي لتوضيحه هو \(U_2 \Lambda U_2^T\). للقيام بذلك، يمكننا التعبير عنها من حيث المصفوفات التي تم تقييمها بالفعل:

\[\begin{split}\begin{align} U_2 \Lambda U_2^T &= \left(K_{21} U_1 \Lambda^{-1}\right) \Lambda \left(K_{21} U_1 \Lambda^{-1}\right)^T \\&= K_{21} U_1 (\Lambda^{-1} \Lambda) \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} U_1 \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} K_{11}^{-1} K_{21}^T \\&= \left( K_{21} K_{11}^{-\frac12} \right) \left( K_{21} K_{11}^{-\frac12} \right)^T .\end{align}\end{split}\]

أثناء fit، تُقيِّم الفئة Nystroem الأساس \(U_1\)، و تحسب ثابت التطبيع، \(K_{11}^{-\frac12}\). لاحقًا، أثناء transform، يتم تحديد مصفوفة النواة بين الأساس (المُعطى بواسطة السمة components_) ونقاط البيانات الجديدة، X. ثم يتم ضرب هذه المصفوفة في مصفوفة normalization_ للحصول على النتيجة النهائية.

افتراضيًا، يستخدم Nystroem نواة rbf، لكن يمكنه استخدام أي دالة نواة أو مصفوفة نواة مُسبقة الحساب. عدد العينات المُستخدمة - وهو أيضًا أبعاد الميزات المحسوبة - مُعطى بواسطة المعلمة n_components.

أمثلة

• انظر المثال المعنون هندسة الميزات ذات الصلة بالوقت، الذي يُظهر خط أنابيب تعلم آلي فعال يستخدم نواة Nystroem.

6.7.2. نواة دالة الأساس الشعاعي

RBFSampler يبني تعيينًا تقريبيًا لنواة دالة الأساس الشعاعي، والمعروفة أيضًا باسم أحواض المطبخ العشوائية [RR2007]. يمكن استخدام هذا التحويل لنمذجة تعيين نواة صراحةً، قبل تطبيق خوارزمية خطية، على سبيل المثال SVM خطية:

>>> from sklearn.kernel_approximation import RBFSampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> rbf_feature = RBFSampler(gamma=1, random_state=1)
>>> X_features = rbf_feature.fit_transform(X)
>>> clf = SGDClassifier(max_iter=5)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=5)
>>> clf.score(X_features, y)
1.0

يعتمد التعيين على تقريب مونت كارلو لـ قيم النواة. تُجري دالة fit أخذ عينات مونت كارلو، بينما تُجري أسلوب transform تعيين البيانات. بسبب العشوائية الكامنة في العملية، قد تختلف النتائج بين استدعاءات مختلفة لدالة fit.

تأخذ دالة fit وسيطتين: n_components، وهو أبعاد الهدف لتحويل الميزات، و gamma، معلمة نواة RBF. n_components أعلى سيؤدي إلى تقريب أفضل للنواة وسيُعطي نتائج أكثر تشابهًا مع تلك التي تنتجها SVM نواة. لاحظ أن "ملاءمة" دالة الميزة لا تعتمد في الواقع على البيانات المُعطاة لدالة fit. يتم استخدام أبعاد البيانات فقط. يمكن العثور على تفاصيل عن الأسلوب في [RR2007].

لقيمة مُعطاة لـ n_components، غالبًا ما يكون RBFSampler أقل دقة من Nystroem. RBFSampler أرخص في الحساب، مما يجعل استخدام مساحات ميزات أكبر أكثر كفاءة.

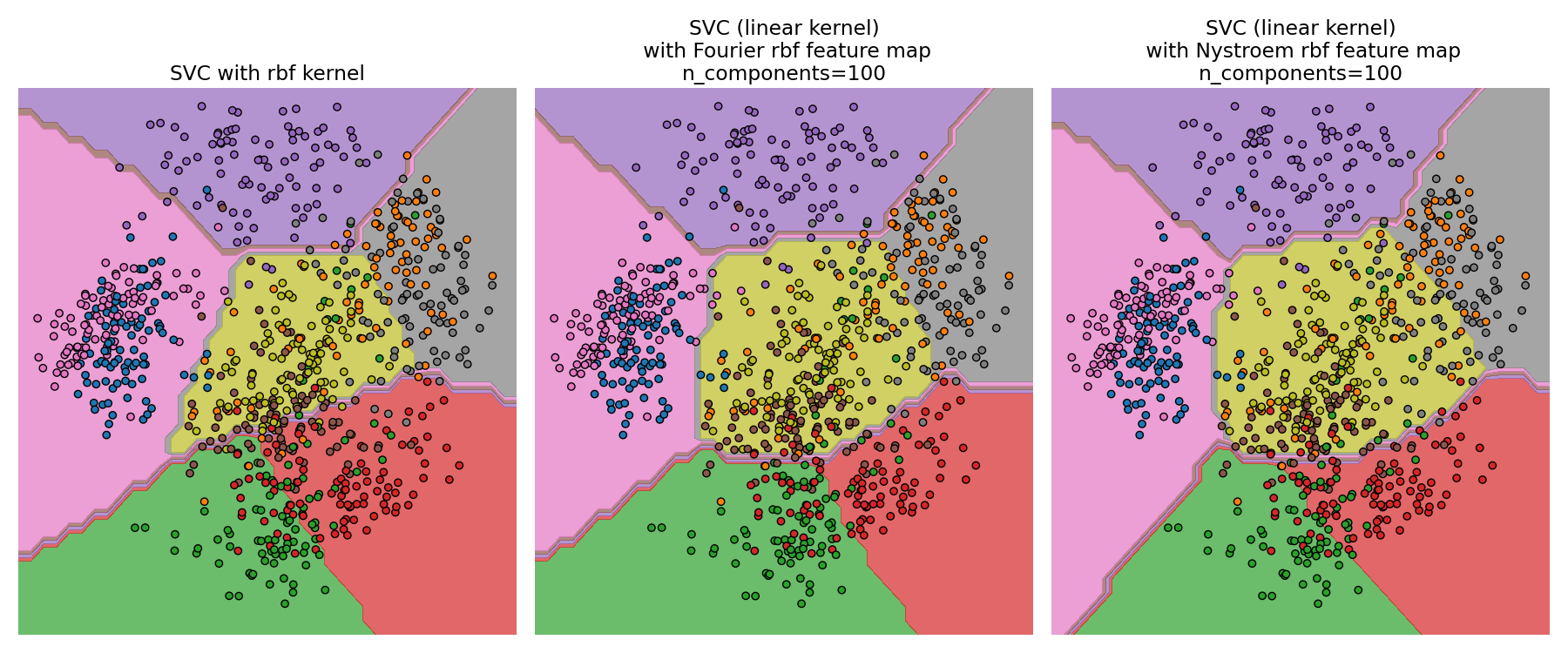
مقارنة نواة RBF دقيقة (يسار) مع التقريب (يمين)

أمثلة

• تقريب خريطة الميزات الصريحة لنواة RBF

6.7.3. نواة Chi التربيعية المضافة

نواة Chi التربيعية المضافة هي نواة على الرسوم البيانية، وغالبًا ما تُستخدم في رؤية الكمبيوتر.

يتم إعطاء نواة Chi التربيعية المضافة كما هو مستخدم هنا بواسطة

\[k(x, y) = \sum_i \frac{2x_iy_i}{x_i+y_i}\]

هذا ليس تمامًا مثل sklearn.metrics.pairwise.additive_chi2_kernel. يُفضل مؤلفو [VZ2010] الإصدار أعلاه لأنه دائمًا موجب مُحدد. نظرًا لأن النواة مضافة، فمن الممكن مُعالجة جميع المكونات \(x_i\) بشكل مُنفصل للتضمين. هذا يجعل من الممكن أخذ عينات من تحويل فورييه على فترات منتظمة، بدلاً من التقريب باستخدام أخذ عينات مونت كارلو.

تُطبق الفئة AdditiveChi2Sampler أخذ العينات الحتمي المكون الحكيم هذا. يتم أخذ عينات من كل مكون \(n\) مرة، مما يُعطي \(2n+1\) أبعاد لكل بُعد إدخال (مُضاعف اثنين ينبع من الجزء الحقيقي والمعقد لتحويل فورييه). في الأدبيات، عادةً ما يتم اختيار \(n\) لتكون 1 أو 2، تحويل مجموعة البيانات إلى الحجم n_samples * 5 * n_features (في حالة \(n=2\)).

يمكن دمج تعيين الميزات التقريبي الذي يُوفره AdditiveChi2Sampler مع تعيين الميزات التقريبي الذي يُوفره RBFSampler لإنتاج تعيين ميزات تقريبي لنواة Chi التربيعية الأسية. انظر [VZ2010] للتفاصيل و [VVZ2010] للجمع مع RBFSampler.

6.7.4. نواة Chi التربيعية المُنحرفة

يتم إعطاء نواة Chi التربيعية المُنحرفة بواسطة:

\[k(x,y) = \prod_i \frac{2\sqrt{x_i+c}\sqrt{y_i+c}}{x_i + y_i + 2c}\]

لها خصائص مُشابهة لنواة Chi التربيعية الأسية التي غالبًا ما تُستخدم في رؤية الكمبيوتر، ولكنها تسمح بتقريب مونت كارلو بسيط لتعيين الميزات.

استخدام SkewedChi2Sampler هو نفسه الاستخدام الموضح أعلاه لـ RBFSampler. الاختلاف الوحيد هو في المعلمة الحرة، التي تُسمى \(c\). للحصول على دافع لهذا التعيين والتفاصيل الرياضية، انظر [LS2010].

6.7.5. تقريب النواة متعددة الحدود عبر Tensor Sketch

نواة متعددة الحدود هي نوع شائع من دوال النواة المُعطاة بواسطة:

\[k(x, y) = (\gamma x^\top y +c_0)^d\]

حيث:

• x و y هما متجهات الإدخال

• d هي درجة النواة

بشكل حدسي، تتكون مساحة ميزات النواة متعددة الحدود من الدرجة d من جميع منتجات الدرجة d الممكنة بين ميزات الإدخال، مما يُمكِّن خوارزميات التعلم التي تستخدم هذه النواة من حساب التفاعلات بين الميزات.

أسلوب TensorSketch [PP2013]، كما هو مُطبق في PolynomialCountSketch، هو أسلوب قابل للتطوير ومستقل عن بيانات الإدخال لتقريب النواة متعددة الحدود. يعتمد على مفهوم Count sketch [WIKICS] [CCF2002]، وهي تقنية لتقليل الأبعاد تُشبه تجزئة الميزات، والتي تستخدم بدلاً من ذلك عدة دوال تجزئة مستقلة. يحصل TensorSketch على Count Sketch للحاصل الضربي الخارجي لمتجهين (أو متجه مع نفسه)، والذي يمكن استخدامه كتقريب لمساحة ميزات النواة متعددة الحدود. على وجه الخصوص، بدلاً من حساب حاصل الضرب الخارجي صراحةً، يحسب TensorSketch Count Sketch للمتجهات ثم يستخدم الضرب متعدد الحدود عبر تحويل فورييه السريع لحساب Count Sketch لحاصل ضربها الخارجي.

بشكل مُريح، تتكون مرحلة تدريب TensorSketch ببساطة من تهيئة بعض المتغيرات العشوائية. وبالتالي فهي مستقلة عن بيانات الإدخال، أي أنها تعتمد فقط على عدد ميزات الإدخال، ولكن ليس على قيم البيانات. بالإضافة إلى ذلك، يمكن لهذا الأسلوب تحويل العينات في \(\mathcal{O}(n_{\text{samples}}(n_{\text{features}} + n_{\text{components}} \log(n_{\text{components}})))\) وقت، حيث \(n_{\text{components}}\) هو بُعد الإخراج المطلوب، مُحدد بواسطة n_components.

أمثلة

• التعلم القابل للتطوير مع تقريب نواة متعددة الحدود

6.7.6. التفاصيل الرياضية

تعتمد أساليب النواة مثل آلات متجه الدعم أو PCA المُستخدمة للنواة على خاصية إعادة إنتاج مساحات هيلبرت للنواة. لأي دالة نواة موجبة مُحددة \(k\) (ما يُسمى نواة Mercer)، من المُضمَّن وجود تعيين \(\phi\) إلى فضاء هيلبرت \(\mathcal{H}\)، بحيث

\[k(x,y) = \langle \phi(x), \phi(y) \rangle\]

حيث \(\langle \cdot, \cdot \rangle\) يُشير إلى حاصل الضرب الداخلي في فضاء هيلبرت.

إذا كانت خوارزمية، مثل آلة متجه دعم خطية أو PCA، تعتمد فقط على حاصل الضرب العددي لنقاط البيانات \(x_i\)، فقد يستخدم المرء قيمة \(k(x_i, x_j)\)، والتي تُقابل تطبيق الخوارزمية على نقاط البيانات المُعيَّنة \(\phi(x_i)\). ميزة استخدام \(k\) هي أن التعيين \(\phi\) لا يجب حسابه صراحةً أبدًا، مما يسمح بميزات كبيرة عشوائية (حتى لانهائية).

أحد عيوب أساليب النواة هو أنه قد يكون من الضروري تخزين العديد من قيم النواة \(k(x_i, x_j)\) أثناء التحسين. إذا تم تطبيق مُصنف مُستخدم للنواة على بيانات جديدة \(y_j\)، فإن \(k(x_i, y_j)\) يحتاج إلى حسابه لإجراء تنبؤات، ربما للعديد من \(x_i\) المختلفة في مجموعة التدريب.

تسمح الفئات في هذه الوحدة الفرعية بتقريب التضمين \(\phi\)، وبالتالي العمل صراحةً مع التمثيلات \(\phi(x_i)\)، مما يُلغي الحاجة إلى تطبيق النواة أو تخزين أمثلة التدريب.

المراجع

[WS2001]

"استخدام أسلوب Nyström لتسريع آلات النواة" Williams, C.K.I.; Seeger, M. - 2001.

[RR2007] (1,2)

"ميزات عشوائية لآلات النواة واسعة النطاق" Rahimi, A. and Recht, B. - Advances in neural information processing 2007,

[LS2010]

"تقديرات فورييه العشوائية لنوى الرسم البياني المُنحرفة المُضاعفة" Li, F., Ionescu, C., and Sminchisescu, C. - Pattern Recognition, DAGM 2010, Lecture Notes in Computer Science.

[VZ2010] (1,2)

"نوى مضافة فعالة عبر تعيينات الميزات الصريحة" Vedaldi, A. and Zisserman, A. - Computer Vision and Pattern Recognition 2010

[VVZ2010]

"تعيينات ميزات RBF مُعممة للكشف الفعال" Vempati, S. and Vedaldi, A. and Zisserman, A. and Jawahar, CV - 2010

[PP2013]

"نوى متعددة الحدود سريعة وقابلة للتطوير عبر تعيينات الميزات الصريحة" Pham, N., & Pagh, R. - 2013

[CCF2002]

"العثور على عناصر متكررة في تدفقات البيانات" Charikar, M., Chen, K., & Farach-Colton - 2002

[WIKICS]

"Wikipedia: Count sketch"