6.6. الإسقاط العشوائي#
تطبق الوحدة النمطية sklearn.random_projection طريقة بسيطة وفعالة من الناحية الحسابية لخفض الأبعاد للبيانات من خلال التداول على كمية محكومة من الدقة (كاختلاف إضافي) لأوقات معالجة أسرع وأحجام نماذج أصغر. تنفذ هذه الوحدة النمطية نوعين من المصفوفات العشوائية غير المنظمة:
مصفوفة عشوائية ذاتية و
مصفوفة عشوائية نادرة.
يتم التحكم في أبعاد وتوزيع مصفوفات الإسقاط العشوائي بحيث يتم الحفاظ على المسافات الزوجية بين أي عينة من مجموعة البيانات. وبالتالي، فإن الإسقاط العشوائي هو تقنية تقريبية مناسبة للأساليب القائمة على المسافة.
المراجع
Sanjoy Dasgupta. 2000. تجارب مع الإسقاط العشوائي. في وقائع المؤتمر السادس عشر حول عدم اليقين في الذكاء الاصطناعي (UAI'00)، Craig Boutilier وMoisés Goldszmidt (محرران). Morgan ناشرو كوفمان، سان فرانسيسكو، كاليفورنيا، الولايات المتحدة الأمريكية، 143-151.
Ella Bingham وHeikki Mannila. 2001. الإسقاط العشوائي في خفض الأبعاد: التطبيقات على بيانات الصور والنصوص. في وقائع المؤتمر السابع ACM SIGKDD الدولي حول اكتشاف المعرفة واستخراج البيانات (KDD '01). ACM، نيويورك، نيويورك، الولايات المتحدة الأمريكية، 245-250.
6.6.1. مبرهنة جونسون-ليندستراوس#
النتيجة النظرية الرئيسية وراء كفاءة الإسقاط العشوائي هي مبرهنة جونسون-ليندستراوس (اقتباس من ويكيبيديا):
في الرياضيات، مبرهنة جونسون-ليندستراوس هي نتيجة تتعلق بالتعميدات ذات التشوه المنخفض للنقاط من الأبعاد العالية إلى فضاء إقليدي منخفض الأبعاد. تنص المبرهنة على أنه يمكن تضمين مجموعة صغيرة من النقاط في مساحة ذات أبعاد عالية في مساحة ذات أبعاد أقل بكثير بطريقة تحافظ على المسافات بين النقاط تقريبًا. يمكن أن تكون الخريطة المستخدمة للتعميد على الأقل ليبشيتز، ويمكن حتى أن تكون إسقاطًا متعامدًا.
معرفة عدد العينات فقط،
يقدر johnson_lindenstrauss_min_dim
تحفظيًا الحد الأدنى لحجم الفضاء العشوائي لضمان تشوه محدود يتم تقديمه بواسطة الإسقاط العشوائي:
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
663
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894, 9868, 11841])
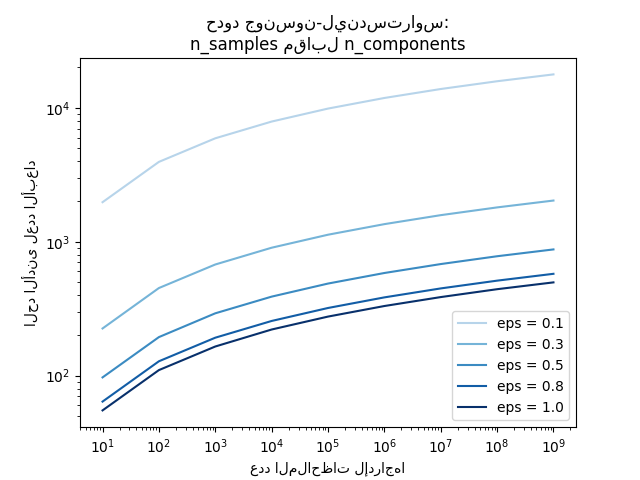
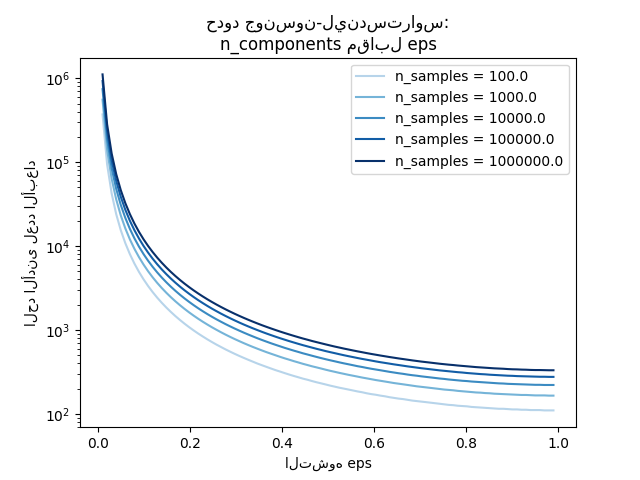
أمثلة
راجع حدود جونسون-ليندستراوس للانغماس مع الإسقاطات العشوائية لشرح نظري حول مبرهنة جونسون-ليندستراوس و التحقق التجريبي باستخدام المصفوفات العشوائية النادرة.
المراجع
Sanjoy Dasgupta وAnupam Gupta، 1999. دليل أولي على مبرهنة جونسون-ليندستراوس.
6.6.2. الإسقاط العشوائي ذاتي#
يقلل GaussianRandomProjection
الأبعاد من خلال إسقاط مساحة الإدخال الأصلية على مصفوفة تم إنشاؤها عشوائيًا
حيث يتم رسم المكونات من التوزيع التالي
\(N(0, \frac{1}{n_{components}})\).
هنا مقتطف صغير يوضح كيفية استخدام محول الإسقاط العشوائي ذاتي:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
6.6.3. الإسقاط العشوائي النادر#
يقلل SparseRandomProjection
الأبعاد من خلال إسقاط مساحة الإدخال الأصلية باستخدام مصفوفة عشوائية نادرة.
المصفوفات العشوائية النادرة هي بديل للمصفوفة العشوائية ذاتية الكثافة التي تضمن جودة تضمين مماثلة مع كونها أكثر كفاءة في الذاكرة وتسمح بحساب أسرع للبيانات المسقطة.
إذا حددنا s = 1 / density، يتم رسم عناصر المصفوفة العشوائية من
حيث \(n_{\text{components}}\) هو حجم الفضاء المسقطة. افتراضيًا، يتم تعيين كثافة العناصر غير الصفرية إلى الحد الأدنى من الكثافة كما أوصى Ping Li et al.: \(1 / \sqrt{n_{\text{features}}}\).
هنا مقتطف صغير يوضح كيفية استخدام محول الإسقاط العشوائي النادر:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
المراجع
D. Achlioptas. 2003. الإسقاط العشوائي الصديق لقواعد البيانات: جونسون-ليندستراوس مع عملات معدنية ثنائية. مجلة علوم الكمبيوتر والنظم 66 (2003) 671-687.
Ping Li، Trevor J. Hastie، وKenneth W. Church. 2006. الإسقاط العشوائي النادر للغاية. في وقائع المؤتمر الدولي الثاني عشر ACM SIGKDD حول اكتشاف المعرفة واستخراج البيانات (KDD '06). ACM، نيويورك، نيويورك، الولايات المتحدة الأمريكية، 287-296.
6.6.4. التحويل العكسي#
للمحولات الإسقاط العشوائي معلمة compute_inverse_components. عندما
يتم تعيينها إلى True، بعد إنشاء مصفوفة components_ العشوائية أثناء التجهيز،
يقوم المحول بحساب العكسي الزائف لهذه المصفوفة وتخزينها كـ
inverse_components_. تحتوي مصفوفة inverse_components_ على الشكل
\(n_{features} \times n_{components}\)، وهي دائمًا مصفوفة كثيفة،
بغض النظر عما إذا كانت مصفوفة المكونات نادرة أو كثيفة. لذا، اعتمادًا على
عدد الميزات والمكونات، قد تستخدم الكثير من الذاكرة.
عند استدعاء طريقة inverse_transform، تقوم بحساب ناتج الضرب للمصفوفة
X ومتجه العكسي للمكونات. إذا تم حساب المكونات العكسية أثناء التجهيز، يتم إعادة استخدامها في كل استدعاء لـ inverse_transform.
وإلا يتم إعادة حسابها في كل مرة، مما قد يكون مكلفًا. النتيجة دائمًا
كثيفة، حتى إذا كانت X نادرة.
هنا مثال صغير يوضح كيفية استخدام ميزة التحويل العكسي:
>>> import numpy as np
>>> from sklearn.random_projection import SparseRandomProjection
>>> X = np.random.rand(100, 10000)
>>> transformer = SparseRandomProjection(
... compute_inverse_components=True
... )
...
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
>>> X_new_inversed = transformer.inverse_transform(X_new)
>>> X_new_inversed.shape
(100, 10000)
>>> X_new_again = transformer.transform(X_new_inversed)
>>> np.allclose(X_new, X_new_again)
True
