1.7. العمليات الغاوسية

العمليات الغاوسية (GP) هي أسلوب تعلم خاضع للإشراف غير بارامتري يُستخدم لحل مشاكل الانحدار و التصنيف الاحتمالي.

مزايا العمليات الغاوسية هي:

• يتداخل التنبؤ مع الملاحظات (على الأقل بالنسبة للنوى المنتظمة).

• التنبؤ احتمالي (غاوسي) بحيث يمكن للمرء حساب فترات ثقة تجريبية واتخاذ القرار بناءً على تلك الفترات إذا كان ينبغي إعادة ملاءمة (ملاءمة على الإنترنت، ملاءمة تكيفية) التنبؤ في بعض مناطق الاهتمام.

• مُتعددة الاستخدامات: يمكن تحديد نوى مُختلفة. يتم توفير نوى شائعة، ولكن من الممكن أيضًا تحديد نوى مُخصصة.

تشمل عيوب العمليات الغاوسية:

• تطبيقنا ليس متفرقًا، أي أنها تستخدم معلومات العينات / الميزات الكاملة لإجراء التنبؤ.

• يفقدون الكفاءة في المساحات عالية الأبعاد - أي عندما يتجاوز عدد الميزات بضع عشرات.

1.7.1. انحدار العملية الغاوسية (GPR)

GaussianProcessRegressor يُطبق العمليات الغاوسية (GP) لـ أغراض الانحدار. لهذا، يجب تحديد المُسبق لـ GP. سيجمع GP هذا المُسبق ودالة الاحتمالية بناءً على عينات التدريب. يسمح بإعطاء نهج احتمالي للتنبؤ عن طريق إعطاء المتوسط و الانحراف المعياري كمخرجات عند التنبؤ.

يُفترض أن يكون متوسط المُسبق ثابتًا وصفرًا (لـ normalize_y=False) أو متوسط بيانات التدريب (لـ normalize_y=True). يتم تحديد تغاير المُسبق عن طريق تمرير كائن نواة. يتم تحسين المعلمات الفائقة للنواة عند ملاءمة GaussianProcessRegressor عن طريق تعظيم الاحتمالية الهامشية اللوغاريتمية (LML) بناءً على optimizer الذي تم تمريره. نظرًا لأن LML قد يحتوي على عدة نقاط مثلى محلية، يمكن بدء المُحسِّن بشكل متكرر عن طريق تحديد n_restarts_optimizer. يتم إجراء التشغيل الأول دائمًا بدءًا من قيم المعلمات الفائقة الأولية للنواة؛ يتم إجراء عمليات التشغيل اللاحقة من قيم المعلمات الفائقة التي تم اختيارها عشوائيًا من نطاق القيم المسموح بها. إذا كانت المعلمات الفائقة الأولية يجب أن تظل ثابتة، فيمكن تمرير None كـ مُحسِّن.

يمكن تحديد مستوى الضوضاء في الأهداف عن طريق تمريره عبر المعلمة alpha، إما عالميًا كقيمة عددية أو لكل نقطة بيانات. لاحظ أن مستوى الضوضاء المُعتدل يمكن أن يكون مفيدًا أيضًا للتعامل مع عدم الاستقرار العددي أثناء الملاءمة لأنه يتم تطبيقه بشكل فعال على أنه تنظيم Tikhonov، أي عن طريق إضافته إلى قطري مصفوفة النواة. 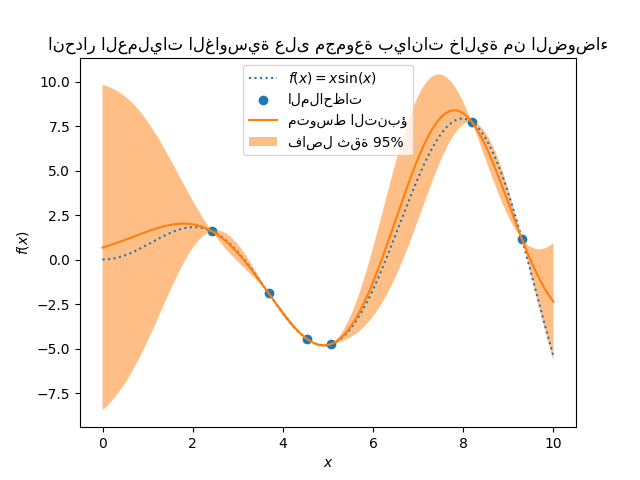بديل لتحديد مستوى الضوضاء صراحةً هو تضمين مكون WhiteKernel في النواة، والذي يمكنه تقدير مستوى الضوضاء العالمي من البيانات (انظر المثال أدناه). يُظهر الشكل أدناه تأثير الهدف الصاخب الذي يتم التعامل معه عن طريق تعيين المعلمة alpha.

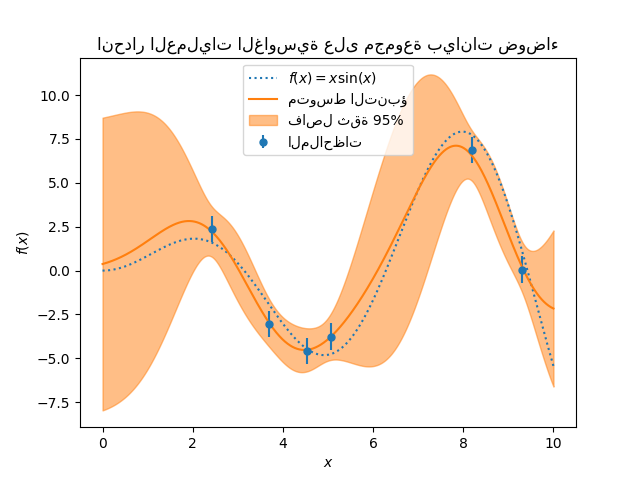
يعتمد التطبيق على الخوارزمية 2.1 من [RW2006]. بالإضافة إلى واجهة برمجة التطبيقات لمُقدِّرات scikit-learn القياسية، GaussianProcessRegressor:

• يسمح بالتنبؤ بدون ملاءمة مُسبقة (بناءً على مُسبق GP)

• يُوفر أسلوبًا إضافيًا sample_y(X)، والذي يُقيِّم العينات المرسومة من GPR (مُسبق أو لاحق) عند مدخلات مُعطاة

• يُظهِر أسلوب log_marginal_likelihood(theta)، والذي يمكن استخدامه خارجيًا لأساليب أخرى لاختيار المعلمات الفائقة، على سبيل المثال، عبر Markov chain Monte Carlo.

أمثلة

• انحدار العمليات الغاوسية: مثال تمهيدي أساسي

• قدرة انحدار العمليات الغاوسية (GPR) على تقدير مستوى ضوضاء البيانات

• مقارنة انحدار kernel ridge وانحدار العمليات الغاوسية

• التنبؤ بمستوى ثاني أكسيد الكربون في مجموعة بيانات Mona Loa باستخدام انحدار العملية الغاوسية (GPR)

1.7.2. تصنيف العملية الغاوسية (GPC)

GaussianProcessClassifier يُطبق العمليات الغاوسية (GP) لـ أغراض التصنيف، وبشكل أكثر تحديدًا للتصنيف الاحتمالي، حيث تأخذ تنبؤات الاختبار شكل احتمالات الفئة. يضع GaussianProcessClassifier مُسبق GP على دالة كامنة \(f\)، والتي يتم ضغطها بعد ذلك من خلال دالة ربط للحصول على التصنيف الاحتمالي. الدالة الكامنة \(f\) هي ما يسمى دالة إزعاج، قيمها غير مُلاحظة وليست ذات صلة بحد ذاتها. الغرض منها هو السماح بصياغة مُلائمة للنموذج، و \(f\) يتم إزالتها (دمجها) أثناء التنبؤ. GaussianProcessClassifier يُطبق دالة ربط لوجستية، والتي لا يمكن حساب التكامل لها تحليليًا ولكن يتم تقريبها بسهولة في الحالة الثنائية.

على عكس إعداد الانحدار، فإن التوزيع اللاحق للدالة الكامنة \(f\) ليس غاوسيًا حتى بالنسبة لمُسبق GP لأن الاحتمالية الغاوسية غير مُناسبة لتصنيفات الفئات المنفصلة. بدلاً من ذلك، يتم استخدام احتمالية غير غاوسية تقابل دالة الربط اللوجستية (logit). يقوم GaussianProcessClassifier بتقريب التوزيع اللاحق غير الغاوسي باستخدام توزيع غاوسي بناءً على تقريب لابلاس. يمكن العثور على مزيد من التفاصيل في الفصل 3 من [RW2006].

يُفترض أن يكون متوسط مُسبق GP صفرًا. يتم تحديد التغاير المُسبق عن طريق تمرير كائن نواة. يتم تحسين المعلمات الفائقة للنواة أثناء ملاءمة GaussianProcessRegressor عن طريق تعظيم الاحتمالية الهامشية اللوغاريتمية (LML) بناءً على optimizer الذي تم تمريره. نظرًا لأن LML قد يحتوي على عدة نقاط مثلى محلية، يمكن بدء المُحسِّن بشكل متكرر عن طريق تحديد n_restarts_optimizer. يتم إجراء التشغيل الأول دائمًا بدءًا من قيم المعلمات الفائقة الأولية للنواة؛ يتم إجراء عمليات التشغيل اللاحقة من قيم المعلمات الفائقة التي تم اختيارها عشوائيًا من نطاق القيم المسموح بها. إذا كانت المعلمات الفائقة الأولية يجب أن تظل ثابتة، فيمكن تمرير None كـ مُحسِّن.

يدعم GaussianProcessClassifier التصنيف متعدد الفئات عن طريق إجراء تدريب وتنبؤ قائم على واحد مقابل الباقي أو واحد مقابل واحد. في واحد مقابل الباقي، يتم ملاءمة مُصنف عملية غاوسية ثنائية واحدة لكل فئة، والتي يتم تدريبها لفصل هذه الفئة عن الباقي. في "one_vs_one"، يتم ملاءمة مُصنف عملية غاوسية ثنائية واحدة لكل زوج من الفئات، والتي يتم تدريبها لفصل هاتين الفئتين. يتم دمج تنبؤات هذه المُتنبئات الثنائية في تنبؤات متعددة الفئات. انظر القسم الخاص بـ التصنيف متعدد الفئات لمزيد من التفاصيل.

في حالة تصنيف العملية الغاوسية، قد يكون "one_vs_one" أقل تكلفة من الناحية الحسابية لأنه يتعين عليه حل العديد من المشاكل التي تتضمن فقط مجموعة فرعية من مجموعة التدريب بأكملها بدلاً من مشاكل أقل على مجموعة البيانات بأكملها. نظرًا لأن تصنيف العملية الغاوسية يتناسب تكعيبيًا مع حجم مجموعة البيانات، فقد يكون هذا أسرع بكثير. ومع ذلك، لاحظ أن "one_vs_one" لا يدعم التنبؤ بتقديرات الاحتمالية ولكن فقط التنبؤات العادية. علاوة على ذلك، لاحظ أن GaussianProcessClassifier لا يُطبق (حتى الآن) تقريب لابلاس متعدد الفئات حقيقيًا داخليًا، ولكن كما نوقش أعلاه، يعتمد على حل العديد من مهام التصنيف الثنائية داخليًا، والتي يتم دمجها باستخدام واحد مقابل الباقي أو واحد مقابل واحد.

1.7.3. أمثلة GPC

1.7.3.1. التنبؤات الاحتمالية مع GPC

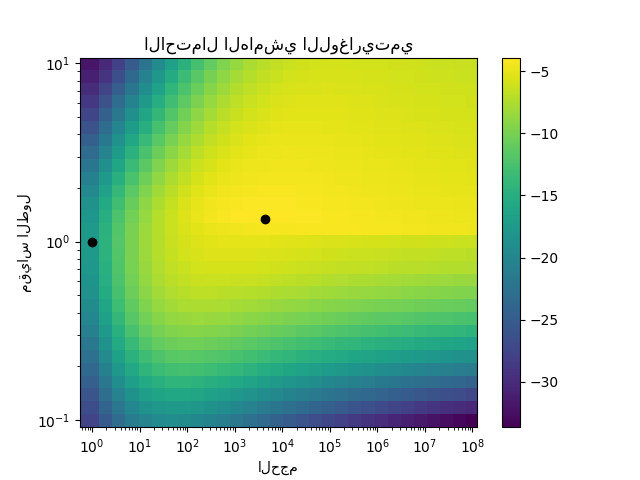
يوضح هذا المثال الاحتمال المتوقع لـ GPC لنواة RBF مع اختيارات مختلفة للمعلمات الفائقة. يُظهر الشكل الأول الاحتمال المتوقع لـ GPC مع معلمات فائقة تم اختيارها عشوائيًا ومع المعلمات الفائقة المقابلة لأقصى احتمالية هامشية لوغاريتمية (LML).

بينما تتمتع المعلمات الفائقة التي تم اختيارها عن طريق تحسين LML بـ LML أكبر بشكل ملحوظ، فإنها تؤدي بشكل أسوأ قليلاً وفقًا لخسارة السجل على بيانات الاختبار. يُظهر الشكل أن هذا يرجع إلى أنها تُظهر تغيرًا حادًا في احتمالات الفئة عند حدود الفئة (وهو أمر جيد) ولكن لديها احتمالات متوقعة قريبة من 0.5 بعيدًا عن حدود الفئة (وهو أمر سيئ). يحدث هذا التأثير غير المرغوب فيه بسبب تقريب لابلاس المستخدم داخليًا بواسطة GPC.

يُظهر الشكل الثاني الاحتمالية الهامشية اللوغاريتمية لاختيارات مختلفة من المعلمات الفائقة للنواة، مع تسليط الضوء على الخيارين لـ المعلمات الفائقة المستخدمة في الشكل الأول بنقاط سوداء.

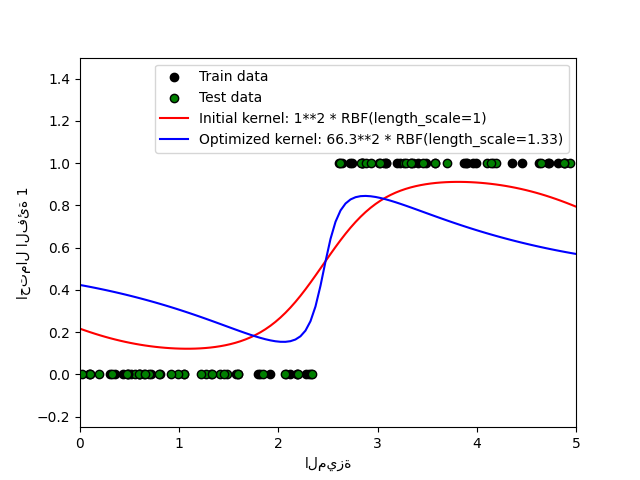
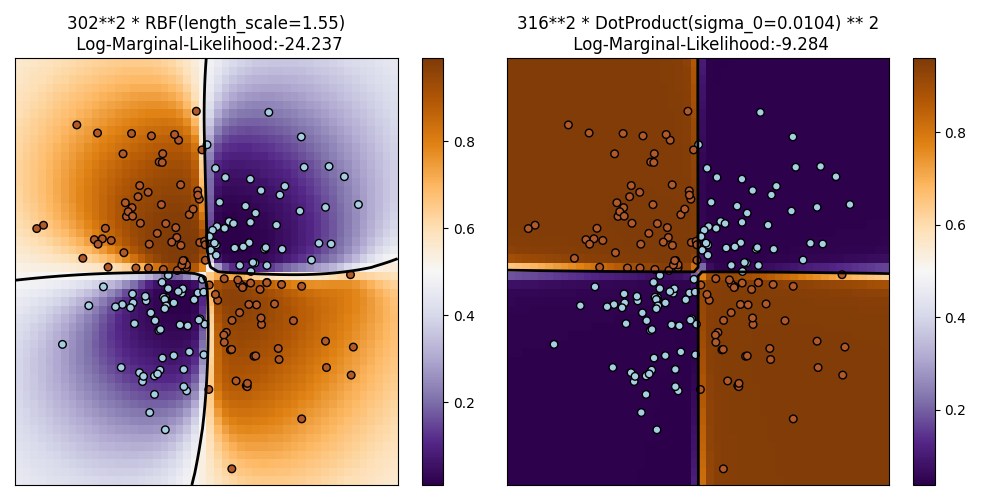
1.7.3.2. توضيح GPC على مجموعة بيانات XOR

يوضح هذا المثال GPC على بيانات XOR. تتم مقارنة نواة ثابتة ومتجانسة (RBF) ونواة غير ثابتة (DotProduct). على هذه المجموعة المعينة من البيانات، تحصل نواة DotProduct على نتائج أفضل بكثير لأن حدود الفئة خطية وتتزامن مع محاور الإحداثيات. ومع ذلك، في الممارسة العملية، غالبًا ما تحصل النوى الثابتة مثل RBF على نتائج أفضل.

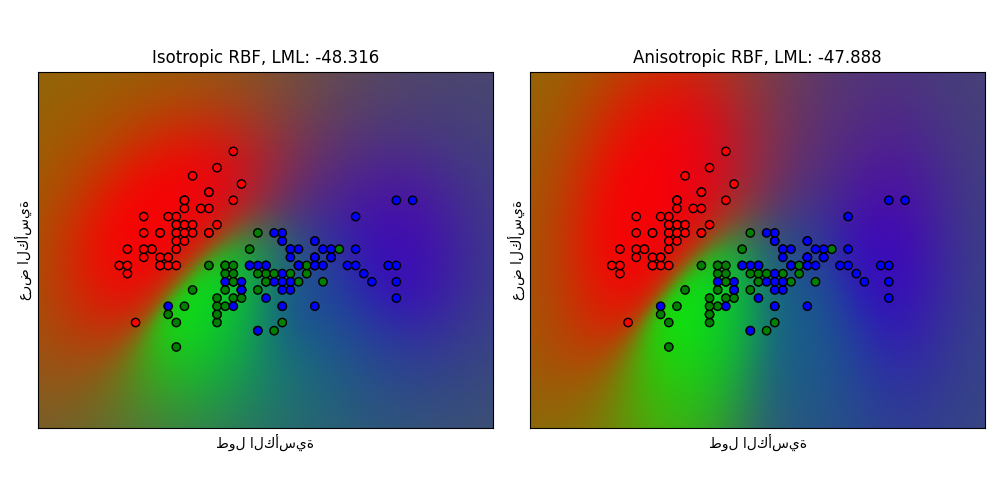
1.7.3.3. تصنيف العملية الغاوسية (GPC) على مجموعة بيانات iris

يوضح هذا المثال الاحتمال المتوقع لـ GPC لنواة RBF متجانسة وغير متجانسة على إصدار ثنائي الأبعاد لمجموعة بيانات iris. هذا يوضح قابلية تطبيق GPC على التصنيف غير الثنائي. تحصل نواة RBF غير المتجانسة على احتمالية هامشية لوغاريتمية أعلى قليلاً عن طريق تعيين مقاييس طول مختلفة لبعدي الميزة.

1.7.4. نوى العمليات الغاوسية

النوى (تُسمى أيضًا "دوال التغاير" في سياق GPs) هي مُكوِّن أساسي لـ GPs التي تُحدد شكل المُسبق واللاحق لـ GP. إنها تُرمِّز الافتراضات على الدالة التي يتم تعلمها عن طريق تحديد "تشابه" نقطتي بيانات مُجتمعتين مع افتراض أن نقاط البيانات المُتشابهة يجب أن يكون لها قيم مستهدفة مُتشابهة. يمكن تمييز فئتين من النوى: تعتمد النوى الثابتة فقط على مسافة نقطتي بيانات وليس على قيمها المُطلقة \(k(x_i, x_j)= k(d(x_i, x_j))\) وبالتالي فهي ثابتة لـ الترجمات في فضاء الإدخال، بينما النوى غير الثابتة تعتمد أيضًا على القيم المحددة لنقاط البيانات. يمكن تقسيم النوى الثابتة إلى نوى متجانسة وغير متجانسة، حيث تكون النوى المتجانسة أيضًا ثابتة للدوران في فضاء الإدخال. لمزيد من التفاصيل، نُشير إلى الفصل 4 من [RW2006]. للحصول على إرشادات حول كيفية الجمع بين النوى المختلفة بشكل أفضل، نُشير إلى [Duv2014].

واجهة برمجة تطبيقات نواة العملية الغاوسية

الاستخدام الرئيسي لـ Kernel هو حساب تغاير GP بين نقاط البيانات. لهذا، يمكن استدعاء أسلوب __call__ للنواة. هذا الأسلوب يمكن استخدامه إما لحساب "التغاير التلقائي" لجميع أزواج نقاط البيانات في مصفوفة ثنائية الأبعاد X، أو "التغاير المتبادل" لجميع مجموعات نقاط البيانات لمصفوفة ثنائية الأبعاد X مع نقاط البيانات في مصفوفة ثنائية الأبعاد Y. الهوية التالية صحيحة لجميع النوى k (باستثناء WhiteKernel): k(X) == K(X, Y=X)

إذا تم استخدام قطري التغاير التلقائي فقط، فيمكن استدعاء أسلوب diag() لنواة، وهو أكثر كفاءة من الناحية الحسابية من الاستدعاء المُكافئ لـ __call__: np.diag(k(X, X)) == k.diag(X)

يتم تحديد معلمات النوى بواسطة متجه \(\theta\) من المعلمات الفائقة. هذه المعلمات الفائقة يمكنها على سبيل المثال التحكم في مقاييس الطول أو دورية النواة (انظر أدناه). تدعم جميع النوى حساب التدرجات التحليلية لتغاير النواة التلقائي فيما يتعلق بـ \(log(\theta)\) عبر التعيين eval_gradient=True في أسلوب __call__. أي، يتم إرجاع مصفوفة (len(X), len(X), len(theta)) حيث الإدخال [i, j, l] يحتوي على \(\frac{\partial k_\theta(x_i, x_j)}{\partial log(\theta_l)}\). يستخدم هذا التدرج بواسطة العملية الغاوسية (كل من المُنحدِر والمُصنف) في حساب تدرج الاحتمالية الهامشية اللوغاريتمية، والذي بدوره يُستخدم لتحديد قيمة \(\theta\)، التي تُعظِّم الاحتمالية الهامشية اللوغاريتمية، عبر الصعود التدرجي. لكل معلمة فائقة، القيمة الأولية و الحدود يجب تحديدها عند إنشاء مثيل للنواة. يمكن الحصول على القيمة الحالية لـ \(\theta\) وتعيينها عبر الخاصية theta لكائن النواة. علاوة على ذلك، يمكن الوصول إلى حدود المعلمات الفائقة بواسطة خاصية bounds للنواة. لاحظ أن كلا الخاصيتين (theta و bounds) تُعيدان قيمًا مُحوَّلة لوغاريتميًا للقيم المستخدمة داخليًا نظرًا لأنها عادةً ما تكون أكثر ملاءمة للتحسين القائم على التدرج. يتم تخزين مواصفات كل معلمة فائقة على شكل مثيل لـ Hyperparameter في النواة المعنية. لاحظ أن النواة التي تستخدم معلمة فائقة باسم "x" يجب أن تحتوي على السمتين self.x و self.x_bounds.

الفئة الأساسية المُجردة لجميع النوى هي Kernel. تُطبق Kernel واجهة مُشابهة لـ BaseEstimator، وتُوفر أساليب get_params() و set_params() و clone(). يسمح هذا بتعيين قيم النواة أيضًا عبر مُقدِّرات التعريف مثل Pipeline أو GridSearchCV. لاحظ أنه نظرًا للبنية المُتداخلة للنوى (عن طريق تطبيق عوامل التشغيل للنواة، انظر أدناه)، فإن أسماء معلمات النواة قد تُصبح مُعقدة نسبيًا. بشكل عام، بالنسبة لعامل تشغيل النواة الثنائي، تتم إضافة بادئة k1__ لمعلمات المعامل الأيسر و k2__ لمعلمات المعامل الأيمن. أسلوب راحة إضافي هو clone_with_theta(theta)، الذي يُعيد نسخة مُستنسخة من النواة ولكن مع تعيين المعلمات الفائقة إلى theta. مثال توضيحي:

>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
k1 : 1**2 * RBF(length_scale=0.5)
k1__k1 : 1**2
k1__k1__constant_value : 1.0
k1__k1__constant_value_bounds : (0.0, 10.0)
k1__k2 : RBF(length_scale=0.5)
k1__k2__length_scale : 0.5
k1__k2__length_scale_bounds : (0.0, 10.0)
k2 : RBF(length_scale=2)
k2__length_scale : 2.0
k2__length_scale_bounds : (0.0, 10.0)
>>> print(kernel.theta)  # ملاحظة: مُحوَّلة لوغاريتميًا
[ 0.         -0.69314718  0.69314718]
>>> print(kernel.bounds)  # ملاحظة: مُحوَّلة لوغاريتميًا
[[      -inf 2.30258509]
[      -inf 2.30258509]
[      -inf 2.30258509]]

جميع نوى العمليات الغاوسية قابلة للتشغيل البيني مع sklearn.metrics.pairwise والعكس صحيح: يمكن تمرير مثيلات الفئات الفرعية لـ Kernel كـ metric إلى pairwise_kernels من sklearn.metrics.pairwise. علاوة على ذلك، يمكن استخدام دوال النواة من pairwise كنوى GP باستخدام فئة التغليف PairwiseKernel. التحذير الوحيد هو أن تدرج المعلمات الفائقة ليس تحليليًا ولكنه رقمي وجميع تلك النوى تدعم المسافات المتجانسة فقط. تعتبر المعلمة gamma معلمة فائقة ويمكن تحسينها. يتم تعيين معلمات النواة الأخرى مباشرةً عند التهيئة وتظل ثابتة.

1.7.4.1. النوى الأساسية

يمكن استخدام نواة ConstantKernel كجزء من نواة Product حيث تُغيّر مقياس حجم العامل الآخر (النواة) أو كجزء من نواة Sum، حيث تُعدِّل متوسط العملية الغاوسية. يعتمد على معلمة \(constant\_value\). يتم تعريفه على النحو التالي:

\[k(x_i, x_j) = constant\_value \;\forall\; x_1, x_2\]

حالة الاستخدام الرئيسية لنواة WhiteKernel هي كجزء من نواة مجموع حيث تُفسر مكون الضوضاء للإشارة. ضبط معلمتها \(noise\_level\) يقابل تقدير مستوى الضوضاء. يتم تعريفه على النحو التالي:

\[k(x_i, x_j) = noise\_level \text{ if } x_i == x_j \text{ else } 0\]

1.7.4.2. عوامل تشغيل النواة

يأخذ عوامل تشغيل النواة نواة أساسية واحدة أو اثنتين ويجمعهما في نواة جديدة. تأخذ نواة Sum نواتين \(k_1\) و \(k_2\) وتجمعهما عبر \(k_{sum}(X, Y) = k_1(X, Y) + k_2(X, Y)\). تأخذ نواة Product نواتين \(k_1\) و \(k_2\) وتجمعهما عبر \(k_{product}(X, Y) = k_1(X, Y) * k_2(X, Y)\). تأخذ نواة Exponentiation نواة أساسية واحدة ومعلمة عددية \(p\) وتجمعهما عبر \(k_{exp}(X, Y) = k(X, Y)^p\). لاحظ أنه تم تجاوز الأساليب السحرية __add__ و __mul___ و __pow__ على كائنات Kernel، لذلك يمكن للمرء استخدام على سبيل المثال RBF() + RBF() كـ اختصار لـ Sum(RBF(), RBF()).

1.7.4.3. دالة أساس نصف القطر (RBF)

نواة RBF هي نواة ثابتة. تُعرف أيضًا باسم نواة "الأس التربيعي". يتم تحديد معلماتها بواسطة معلمة مقياس الطول \(l>0\)، والتي يمكن أن تكون إما عددية (متغير متجانس للنواة) أو متجه بنفس عدد أبعاد المدخلات \(x\) (متغير غير متجانس للنواة). يتم إعطاء النواة بواسطة:

\[k(x_i, x_j) = \text{exp}\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)\]

حيث \(d(\cdot, \cdot)\) هي مسافة إقليدية. هذه النواة قابلة للاشتقاق بلا حدود، مما يعني أن GPs بهذه النواة كدالة تغاير لها مُشتقات مربعة متوسطة لجميع الرتب، وبالتالي فهي سلسة جدًا. يظهر المُسبق واللاحق لـ GP الناتج عن نواة RBF في الشكل التالي:

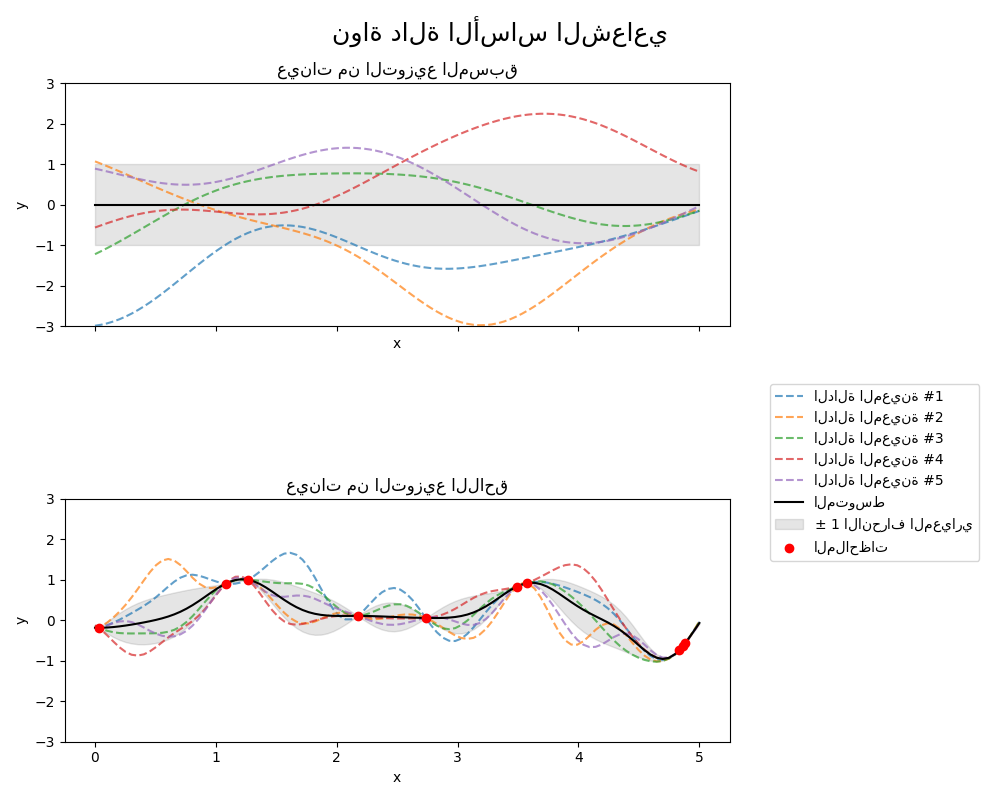
1.7.4.4. نواة Matérn

نواة Matern هي نواة ثابتة وتعميم لـ نواة RBF. لديها معلمة إضافية \(\nu\) التي تتحكم في سلاسة الدالة الناتجة. يتم تحديد معلماتها بواسطة معلمة مقياس الطول \(l>0\)، والتي يمكن أن تكون إما عددية (متغير متجانس للنواة) أو متجه بنفس عدد أبعاد المدخلات \(x\) (متغير غير متجانس للنواة).

التطبيق الرياضي لنواة Matérn

يتم إعطاء النواة بواسطة:

\[k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)^\nu K_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg),\]

حيث \(d(\cdot,\cdot)\) هي مسافة إقليدية، \(K_\nu(\cdot)\) هي دالة Bessel مُعدلة و \(\Gamma(\cdot)\) هي دالة جاما. عندما \(\nu\rightarrow\infty\)، تتقارب نواة Matérn مع نواة RBF. عندما \(\nu = 1/2\)، تُصبح نواة Matérn مطابقة لنواة الأس المُطلق، أي،

\[k(x_i, x_j) = \exp \Bigg(- \frac{1}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{1}{2}\]

على وجه الخصوص، \(\nu = 3/2\):

\[k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{3}}{l} d(x_i , x_j )\Bigg) \exp \Bigg(-\frac{\sqrt{3}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{3}{2}\]

و \(\nu = 5/2\):

\[k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{5}}{l} d(x_i , x_j ) +\frac{5}{3l} d(x_i , x_j )^2 \Bigg) \exp \Bigg(-\frac{\sqrt{5}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{5}{2}\]

هي اختيارات شائعة لتعلم الدوال التي لا يُمكن اشتقاقها بلا حدود (كما هو مُفترض بواسطة نواة RBF) ولكن على الأقل مرة واحدة (\(\nu = 3/2\)) أو مرتين قابلة للاشتقاق (\(\nu = 5/2\)).

مرونة التحكم في سلاسة الدالة التي تم تعلمها عبر \(\nu\) تسمح بالتكيف مع خصائص العلاقة الوظيفية الأساسية الحقيقية.

يظهر المُسبق واللاحق لـ GP الناتج عن نواة Matérn في الشكل التالي:

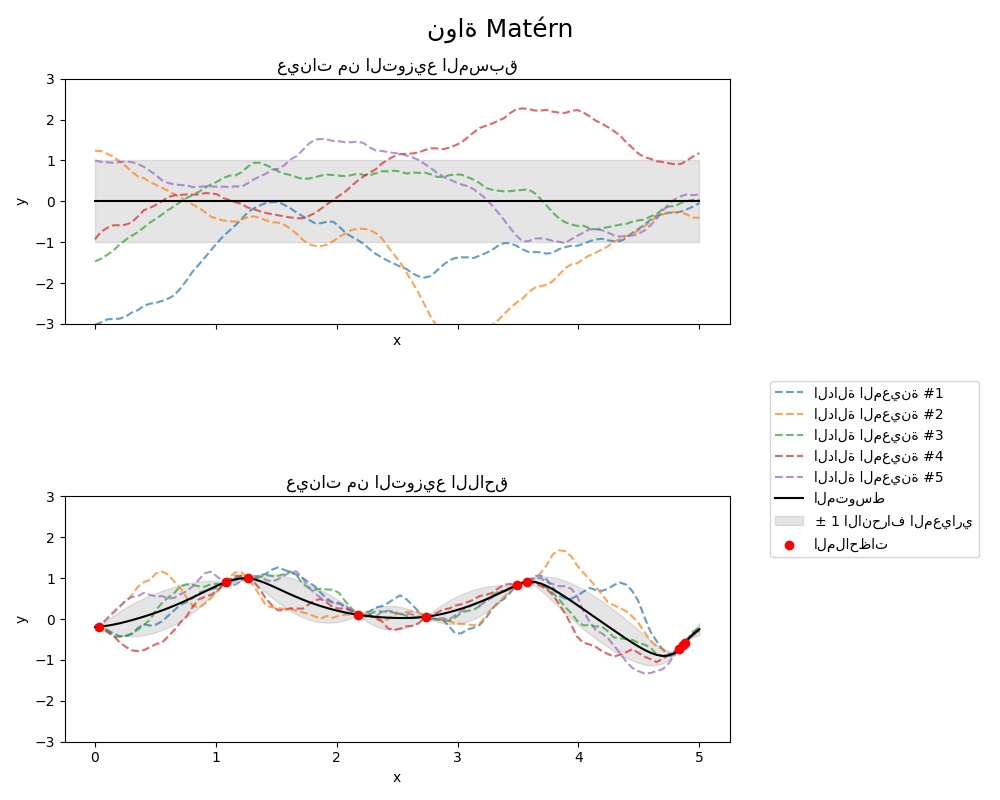
راجع [RW2006], pp84 لمزيد من التفاصيل حول المتغيرات المختلفة لنواة Matérn.

1.7.4.5. نواة تربيعية عقلانية

يمكن اعتبار نواة RationalQuadratic خليط مقياس (مجموع لا نهائي) لنوى RBF ذات مقاييس طول مميزة مختلفة. يتم تحديد معلماتها بواسطة معلمة مقياس الطول \(l>0\) ومعلمة خليط المقياس \(\alpha>0\) يتم دعم المتغير المتجانس فقط حيث \(l\) هو عدد قياسي في الوقت الحالي. يتم إعطاء النواة بواسطة:

\[k(x_i, x_j) = \left(1 + \frac{d(x_i, x_j)^2}{2\alpha l^2}\right)^{-\alpha}\]

يظهر المُسبق واللاحق لـ GP الناتج عن نواة RationalQuadratic في الشكل التالي:

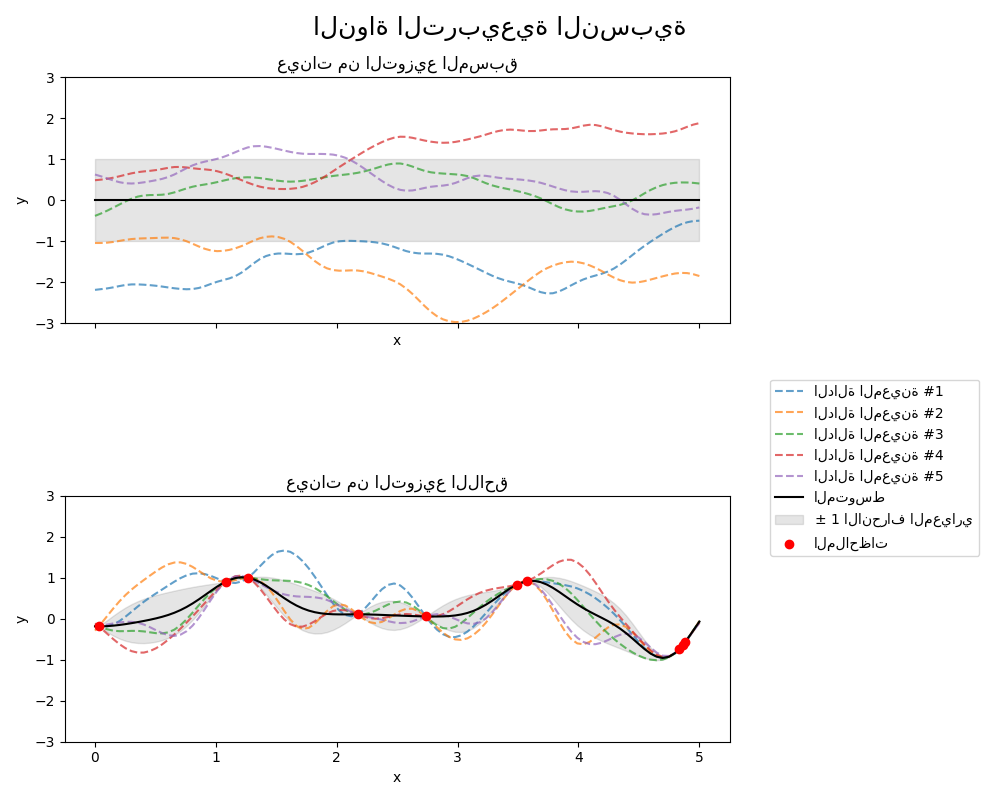
1.7.4.6. نواة Exp-Sine-Squared

تسمح نواة ExpSineSquared بنمذجة الدوال الدورية. يتم تحديد معلماتها بواسطة معلمة مقياس الطول \(l>0\) ومعلمة دورية \(p>0\). يتم دعم المتغير المتجانس فقط حيث \(l\) هو عدد قياسي في الوقت الحالي. يتم إعطاء النواة بواسطة:

\[k(x_i, x_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x_i, x_j) / p) }{ l^ 2} \right)\]

يظهر المُسبق واللاحق لـ GP الناتج عن نواة ExpSineSquared في الشكل التالي:

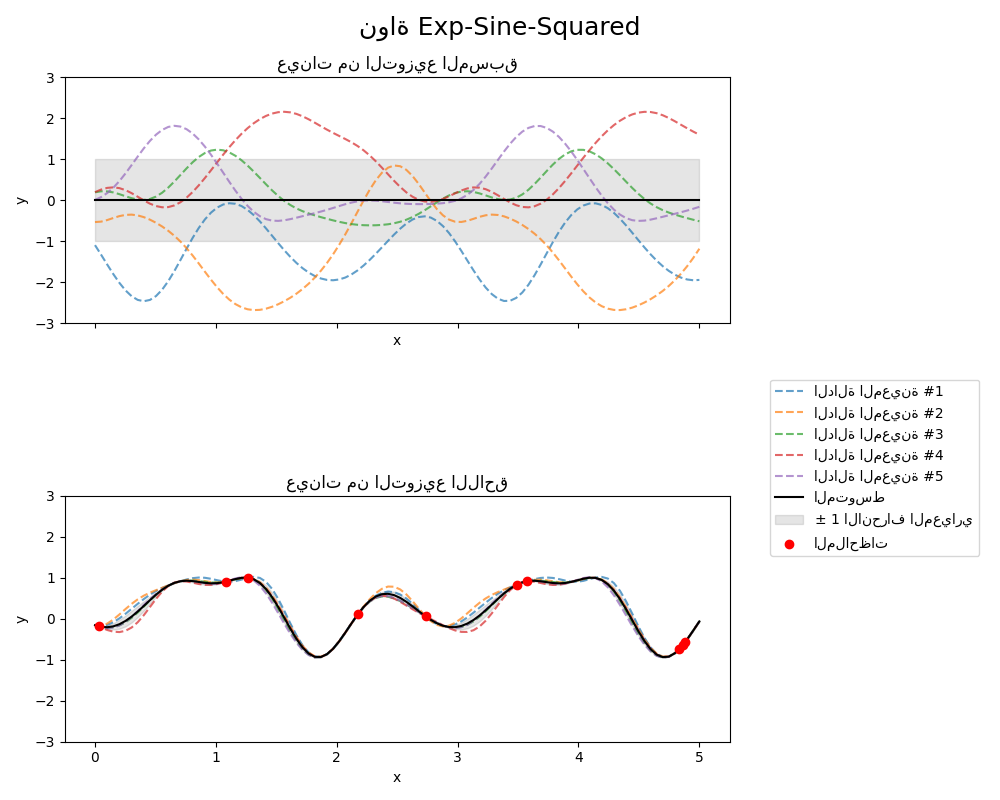
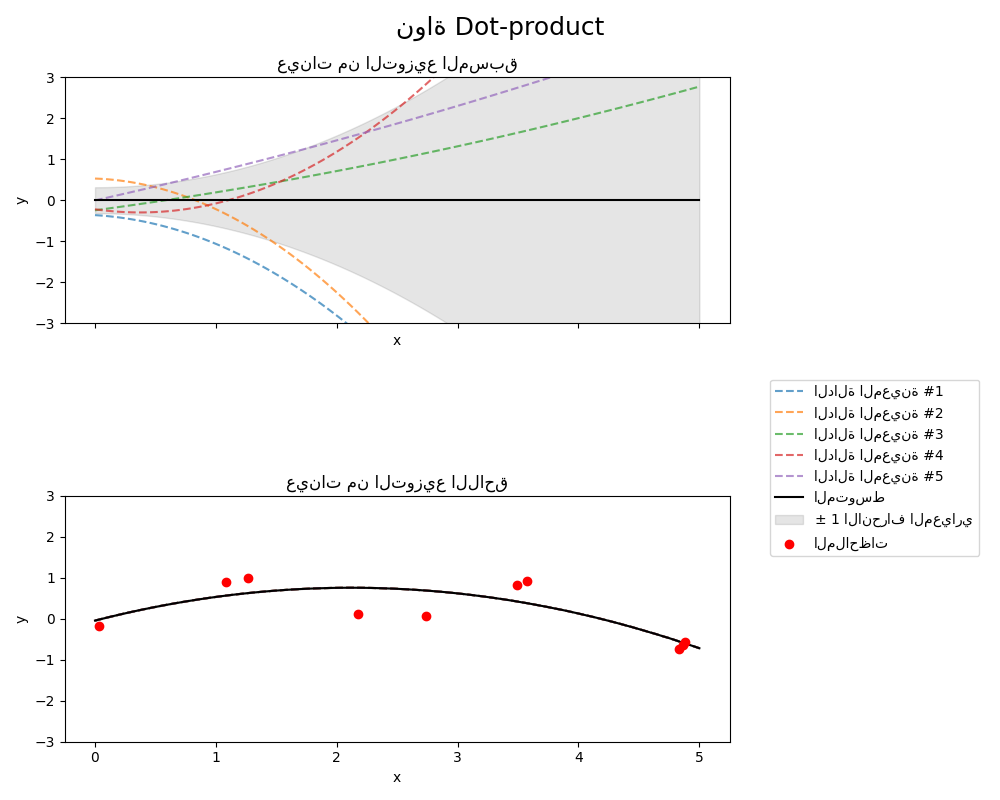
1.7.4.7. نواة Dot-Product

نواة DotProduct غير ثابتة ويمكن الحصول عليها من الانحدار الخطي عن طريق وضع مُسبقات \(N(0, 1)\) على معاملات \(x_d (d = 1, . . . , D)\) ومُسبق \(N(0, \sigma_0^2)\) على التحيز. نواة DotProduct ثابتة لدوران الإحداثيات حول الأصل، ولكن ليس للترجمات. يتم تحديد معلماتها بواسطة معلمة \(\sigma_0^2\). لـ \(\sigma_0^2 = 0\)، تُسمى النواة النواة الخطية المتجانسة، وإلا فهي غير متجانسة. يتم إعطاء النواة بواسطة

\[k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j\]

عادةً ما يتم دمج نواة DotProduct مع الأس. مثال بأس 2 موضح في الشكل التالي:

1.7.4.8. المراجع

[RW2006] (1,2,3,4)

Carl E. Rasmussen and Christopher K.I. Williams, "العمليات الغاوسية للتعلم الآلي", MIT Press 2006

[Duv2014]

David Duvenaud, "كتاب طبخ النواة: نصائح حول دوال التغاير", 2014