1.10. شجرة القرار#

شجرة القرار (DTs) هي طريقة تعليم خاضع للإشراف غير معلم تستخدم لـ التصنيف و الانحدار. الهدف هو إنشاء نموذج يتنبأ بقيمة متغير الهدف من خلال تعلم قواعد قرار بسيطة مستنبطة من ميزات البيانات. يمكن اعتبار الشجرة على أنها تقريب ثابت.

على سبيل المثال، في المثال أدناه، تتعلم أشجار القرار من البيانات لتقريب منحنى الجيب باستخدام مجموعة من قواعد القرار if-then-else. كلما كانت الشجرة أعمق، كلما كانت قواعد القرار أكثر تعقيدًا، وكلما كان النموذج أكثر ملاءمة.

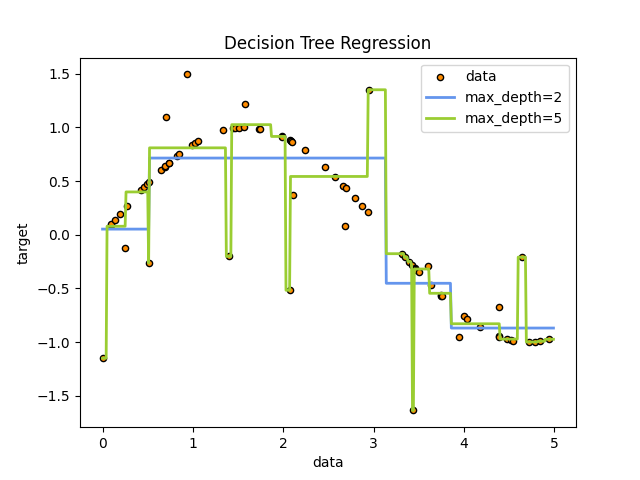
../_images/sphx_glr_plot_tree_regression_001.png

بعض مزايا أشجار القرار هي:

  • سهلة الفهم والتفسير. يمكن تصور الأشجار.

  • تتطلب القليل من الإعداد المسبق للبيانات. تتطلب التقنيات الأخرى عادةً تطبيع البيانات، ويجب إنشاء المتغيرات الوهمية وإزالة القيم الفارغة. تدعم بعض الأشجار والمجموعات خوارزمية دعم القيم المفقودة.

  • تكلفة استخدام الشجرة (أي التنبؤ بالبيانات) لوغاريتمية في عدد نقاط البيانات المستخدمة لتدريب الشجرة.

  • قادرة على التعامل مع البيانات الرقمية والفئوية. ومع ذلك، فإن تنفيذ scikit-learn لا يدعم المتغيرات الفئوية في الوقت الحالي. عادة ما تكون التقنيات الأخرى متخصصة في تحليل مجموعات البيانات التي تحتوي على نوع واحد فقط من المتغيرات. راجع الخوارزميات للحصول على مزيد من المعلومات.

  • قادرة على التعامل مع المشكلات متعددة المخرجات.

  • تستخدم نموذج الصندوق الأبيض. إذا كانت حالة معينة قابلة للملاحظة في نموذج، فيمكن تفسير التفسير للشرط بسهولة بواسطة المنطق البولي. على النقيض من ذلك، في نموذج الصندوق الأسود (مثل الشبكة العصبية الاصطناعية)، قد تكون النتائج أكثر صعوبة في التفسير.

  • من الممكن التحقق من صحة نموذج باستخدام الاختبارات الإحصائية. هذا يجعل من الممكن مراعاة موثوقية النموذج.

  • تؤدي جيدًا حتى إذا تم انتهاك افتراضاتها إلى حد ما بواسطة النموذج الحقيقي الذي تم توليد البيانات منه.

تشمل عيوب أشجار القرار ما يلي:

  • يمكن لمُتعلمي شجرة القرار إنشاء أشجار معقدة للغاية لا تعمم البيانات جيدًا. يُعرف هذا بـ "الإفراط في الملاءمة". الآليات مثل التقليم، وتحديد الحد الأدنى لعدد العينات المطلوبة في عقدة ورقة أو تحديد الحد الأقصى لعمق الشجرة ضرورية لتجنب هذه المشكلة.

  • يمكن أن تكون أشجار القرار غير مستقرة لأن الاختلافات الصغيرة في البيانات قد تؤدي إلى توليد شجرة مختلفة تمامًا. يتم تخفيف هذه المشكلة باستخدام أشجار القرار داخل مجموعة.

  • تنبؤات أشجار القرار ليست سلسة ولا مستمرة، ولكنها تقريبات ثابتة كما هو موضح في الشكل أعلاه. لذلك، فهي ليست جيدة في الاستقراء.

  • مشكلة تعلم شجرة قرار مثالية معروفة بأنها NP-complete تحت عدة جوانب من المثالية وحتى للمفاهيم البسيطة. وبالتالي، تستند خوارزميات تعلم شجرة القرار العملية إلى خوارزميات تقريبية مثل الخوارزمية الجشعة حيث يتم اتخاذ قرارات محلية مثالية في كل عقدة. لا يمكن لهذه الخوارزميات أن تضمن عودة شجرة القرار العالمية المثالية. يمكن تخفيف هذا عن طريق تدريب أشجار متعددة في متعلم مجموعة، حيث يتم أخذ العينات من الميزات والعينات عشوائيًا مع الاستبدال.

  • هناك مفاهيم يصعب تعلمها لأن أشجار القرار لا تعبر عنها بسهولة، مثل مشكلات XOR أو التكافؤ أو المضاعف.

  • يخلق متعلمو شجرة القرار أشجارًا متحيزة إذا كانت بعض الفئات تهيمن. لذلك، يوصى بتوازن مجموعة البيانات قبل الملاءمة مع شجرة القرار.

1.10.1. التصنيف#

DecisionTreeClassifier هي فئة قادرة على إجراء تصنيف متعدد الفئات على مجموعة بيانات.

كما هو الحال مع المصنفات الأخرى، DecisionTreeClassifier يأخذ كمدخل صفيفين: صفيف X، متفرق أو كثيف، من الشكل (n_samples, n_features) يحمل عينات التدريب، وصفيف Y من القيم الصحيحة، الشكل (n_samples,)، يحمل تسميات الفئة لعينات التدريب:

>>> from sklearn import tree
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)

بعد الملاءمة، يمكن استخدام النموذج للتنبؤ بفئة العينات:

>>> clf.predict([[2., 2.]])
array([1])

في حالة وجود فئات متعددة بنفس الاحتمال الأعلى، فإن المصنف سيتنبأ بالفئة ذات الفهرس الأدنى بين تلك الفئات.

كبديل لإخراج فئة محددة، يمكن التنبؤ باحتمالية كل فئة، والتي هي جزء من عينات التدريب من الفئة في ورقة:

>>> clf.predict_proba([[2., 2.]])
array([[0., 1.]])

DecisionTreeClassifier قادر على كل من التصنيف الثنائي (حيث التسميات هي [-1, 1]) والتصنيف متعدد الفئات (حيث التسميات هي [0, ..., K-1]).

باستخدام مجموعة بيانات Iris، يمكننا إنشاء شجرة كما يلي:

>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, y)

بمجرد التدريب، يمكنك رسم الشجرة باستخدام دالة plot_tree:

>>> tree.plot_tree(clf)
[...]
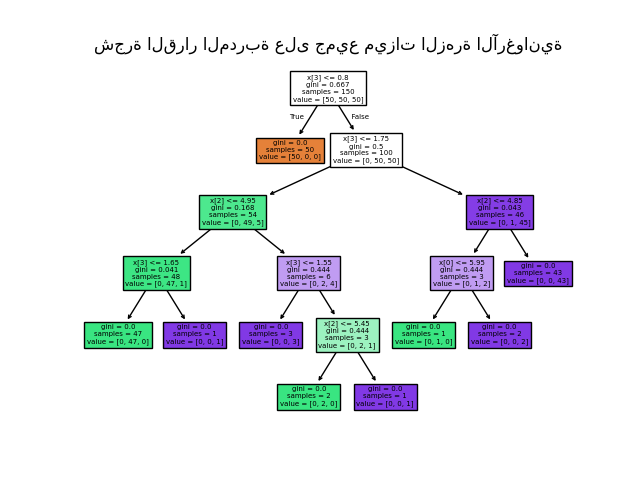
../_images/sphx_glr_plot_iris_dtc_002.png
طرق بديلة لتصدير الأشجار#

يمكننا أيضًا تصدير الشجرة بتنسيق Graphviz <https://www.graphviz.org/> باستخدام مصدر التصدير export_graphviz. إذا كنت تستخدم مدير الحزم conda، فيمكن تثبيت ثنائيات graphviz وحزمة بايثون باستخدام conda install python-graphviz.

يمكن أيضًا تنزيل ثنائيات graphviz من صفحة مشروع graphviz الرئيسية، وتثبيت الغلاف البايثوني من pypi باستخدام pip install graphviz.

فيما يلي مثال على تصدير graphviz للشجرة المدربة على مجموعة بيانات Iris بالكامل؛ يتم حفظ النتائج في ملف إخراج iris.pdf:

>>> import graphviz 
>>> dot_data = tree.export_graphviz(clf, out_file=None) 
>>> graph = graphviz.Source(dot_data) 
>>> graph.render("iris")

يدعم مصدر التصدير export_graphviz أيضًا مجموعة متنوعة من الخيارات الجمالية، بما في ذلك تلوين العقد حسب فئتها (أو قيمتها للانحدار) واستخدام أسماء المتغيرات والفئات الصريحة إذا لزم الأمر. كما تعرض دفاتر Jupyter هذه المخططات تلقائيًا:

>>> dot_data = tree.export_graphviz(clf, out_file=None, 
...                      feature_names=iris.feature_names,  
...                      class_names=iris.target_names,  
...                      filled=True, rounded=True)  
>>> graph = graphviz.Source(dot_data)  
>>> graph
../_images/iris.svg
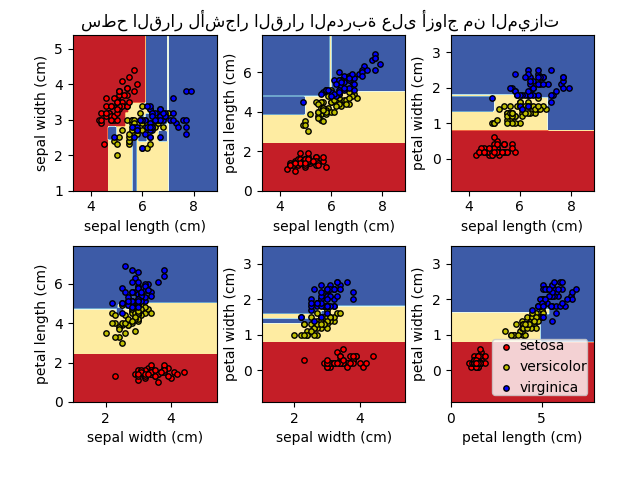
../_images/sphx_glr_plot_iris_dtc_001.png

بدلاً من ذلك، يمكن أيضًا تصدير الشجرة بتنسيق نصي باستخدام الدالة export_text. هذه الطريقة لا تتطلب تثبيت مكتبات خارجية وهي أكثر إحكامًا:

>>> from sklearn.datasets import load_iris
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.tree import export_text
>>> iris = load_iris()
>>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2)
>>> decision_tree = decision_tree.fit(iris.data, iris.target)
>>> r = export_text(decision_tree, feature_names=iris['feature_names'])
>>> print(r)
|--- petal width (cm) <= 0.80
|   |--- class: 0
|--- petal width (cm) >  0.80
|   |--- petal width (cm) <= 1.75
|   |   |--- class: 1
|   |--- petal width (cm) >  1.75
|   |   |--- class: 2

أمثلة

1.10.2. الانحدار#

../_images/sphx_glr_plot_tree_regression_001.png

يمكن أيضًا تطبيق أشجار القرار على مشكلات الانحدار، باستخدام فئة DecisionTreeRegressor.

كما هو الحال في إعداد التصنيف، ستأخذ طريقة الملاءمة كوسيط صفيفين X و y، فقط في هذه الحالة يُتوقع أن تكون القيم y قيمًا عشرية بدلاً من القيم الصحيحة:

>>> from sklearn import tree
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])

أمثلة

1.10.3. المشكلات متعددة المخرجات#

المشكلة متعددة المخرجات هي مشكلة تعلم مشرف مع عدة مخرجات للتنبؤ، أي عندما يكون Y مصفوفة ثنائية الأبعاد من الشكل (n_samples, n_outputs).

عندما لا يوجد ارتباط بين المخرجات، فإن طريقة بسيطة جدًا لحل هذا النوع من المشكلات هي بناء n نماذج مستقلة، أي واحدة لكل مخرج، ثم استخدام تلك النماذج للتنبؤ بشكل مستقل بكل واحد من المخرجات n. ومع ذلك، نظرًا لأنه من المحتمل أن تكون قيم الإخراج المتعلقة بنفس الإدخال مترابطة، فإن طريقة أفضل غالبًا هي بناء نموذج واحد قادر على التنبؤ بجميع المخرجات n في نفس الوقت. أولاً، يتطلب وقت تدريب أقل نظرًا لأنه يتم بناء مقدر واحد فقط. ثانيًا، قد تزداد دقة التعميم للمقدر الناتج غالبًا.

فيما يتعلق بأشجار القرار، يمكن استخدام هذه الاستراتيجية بسهولة لدعم المشكلات متعددة المخرجات. يتطلب هذا التغييرات التالية:

  • تخزين n قيم الإخراج في الأوراق، بدلاً من 1؛

  • استخدام معايير التقسيم التي تحسب متوسط الانخفاض عبر جميع

n المخرجات.

تدعم هذه الوحدة النمطية المشكلات متعددة المخرجات من خلال تنفيذ هذه الاستراتيجية في كل من DecisionTreeClassifier و DecisionTreeRegressor. إذا تم ملاءمة شجرة قرار على مصفوفة إخراج Y من الشكل (n_samples, n_outputs)، فإن المقدر الناتج سيقوم بما يلي:

  • إخراج n_output قيم عند predict؛

  • إخراج قائمة من صفائف احتمالات الفئات n_output عند predict_proba.

يتم توضيح استخدام الأشجار متعددة المخرجات للانحدار في انحدار شجرة القرار. في هذا المثال، الإدخال X هو قيمة حقيقية واحدة والمخرجات Y هي جيب وجيب تمام X.

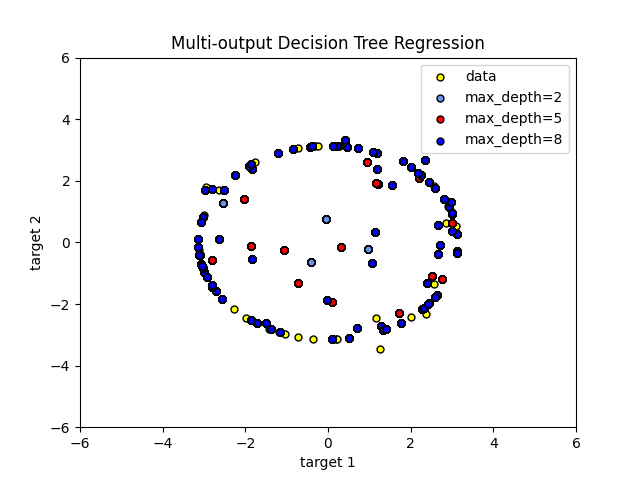
../_images/sphx_glr_plot_tree_regression_002.png

يتم توضيح استخدام الأشجار متعددة المخرجات للتصنيف في اكتمال الوجه باستخدام المُقدرات متعددة المخرجات. في هذا المثال، المدخلات X هي بكسلات النصف العلوي من الوجوه والمخرجات Y هي بكسلات النصف السفلي من تلك الوجوه.

../_images/sphx_glr_plot_multioutput_face_completion_001.png

أمثلة

المراجع

1.10.4. التعقيد#

بشكل عام، تبلغ تكلفة وقت التشغيل لبناء شجرة متوازنة ثنائية \(O(n_{samples}n_{features}\log(n_{samples}))\) ووقت الاستعلام \(O(\log(n_{samples}))\). على الرغم من أن خوارزمية بناء الشجرة تحاول إنشاء أشجار متوازنة، إلا أنها لن تكون متوازنة دائمًا. بافتراض أن الشجرة الفرعية تظل متوازنة تقريبًا، فإن التكلفة في كل عقدة تتكون من \(O(n_{features})\) للعثور على الميزة التي تقدم أكبر انخفاض في معيار عدم النقاء، على سبيل المثال الخسارة اللوجستية (التي تعادل مكسب المعلومات). تبلغ تكلفة هذا \(O(n_{features}n_{samples}\log(n_{samples}))\) في كل عقدة، مما يؤدي إلى تكلفة إجمالية عبر الأشجار بالكامل (عن طريق جمع التكلفة في كل عقدة) من \(O(n_{features}n_{samples}^{2}\log(n_{samples}))\).

1.10.5. نصائح للاستخدام العملي#

  • تميل أشجار القرار إلى الإفراط في الملاءمة على البيانات التي تحتوي على عدد كبير من الميزات. الحصول على النسبة الصحيحة للعينات إلى عدد الميزات أمر مهم، حيث أن الشجرة ذات العينات القليلة في مساحة ذات أبعاد عالية من المحتمل أن تفرط في الملاءمة.

  • ضع في اعتبارك إجراء تقليل الأبعاد (PCA, ICA, أو اختيار الميزات) مسبقًا لإعطاء شجرتك فرصة أفضل للعثور على ميزات تمييزية.

  • فهم بنية شجرة القرار سيساعد في اكتساب المزيد من الرؤى حول كيفية قيام شجرة القرار بالتنبؤات، وهو أمر مهم لفهم الميزات المهمة في البيانات.

  • قم بتصور شجرتك أثناء التدريب باستخدام دالة export

. استخدم max_depth=3 كعمق شجرة أولي للحصول على شعور حول كيفية ملاءمة الشجرة لبياناتك، ثم قم بزيادة العمق.

  • تذكر أن عدد العينات المطلوبة لملء الشجرة يتضاعف

لكل مستوى إضافي تنمو إليه الشجرة. استخدم max_depth للتحكم في حجم الشجرة لمنع الإفراط في الملاءمة.

  • استخدم min_samples_split أو min_samples_leaf لضمان أن العينات المتعددة

تبلغ كل قرار في الشجرة، عن طريق التحكم في الانقسامات التي سيتم النظر فيها. عادةً ما يعني عدد صغير للغاية أن الشجرة ستفرط في الملاءمة، بينما سيمنع عدد كبير الشجرة من تعلم البيانات. جرب min_samples_leaf=5 كقيمة أولية. إذا اختلف حجم العينة بشكل كبير، فيمكن استخدام رقم عشري كنسبة مئوية في هذين المعيارين. بينما يمكن لـ min_samples_split إنشاء أوراق صغيرة بشكل تعسفي، min_samples_leaf يضمن أن يكون لكل ورقة حجم أدنى، مما يتجنب عقد الأوراق منخفضة التباين والمفرطة في الملاءمة في مشكلات الانحدار. للتصنيف مع فئات قليلة، غالبًا ما يكون min_samples_leaf=1 هو الخيار الأفضل.

لاحظ أن min_samples_split يأخذ العينات مباشرةً وبشكل مستقل عن sample_weight، إذا تم توفيره (على سبيل المثال، تتم معاملة العقدة ذات العينات الموزونة m على أنها تحتوي على عينات m بالضبط). ضع في اعتبارك min_weight_fraction_leaf أو min_impurity_decrease إذا كان مطلوبًا مراعاة أوزان العينات عند الانقسامات.

  • قم بتوازن مجموعة بياناتك قبل التدريب لمنع الشجرة من التحيز

نحو الفئات المهيمنة. يمكن إجراء موازنة الفئة عن طريق أخذ عينات عدد متساوٍ من العينات من كل فئة، أو يفضل عن طريق تطبيع مجموع أوزان العينات (sample_weight) لكل فئة إلى نفس القيمة. لاحظ أيضًا أن معايير التقليم المسبق القائمة على الوزن، مثل min_weight_fraction_leaf، ستكون أقل تحيزًا تجاه الفئات المهيمنة من المعايير التي لا تدرك أوزان العينات، مثل min_samples_leaf.

  • إذا كانت العينات موزونة، فسيصبح من الأسهل تحسين بنية الشجرة باستخدام معيار التقليم المسبق القائم على الوزن مثل

min_weight_fraction_leaf، والذي يضمن أن تحتوي عقد الأوراق على جزء على الأقل من إجمالي مجموع أوزان العينات.

  • تستخدم جميع أشجار القرار صفائف np.float32 داخليًا.

إذا لم تكن بيانات التدريب بهذا التنسيق، فسيتم إجراء نسخة من مجموعة البيانات.

  • إذا كانت مصفوفة الإدخال X متفرقة للغاية، فمن المستحسن تحويلها إلى مصفوفة متفرقة

csc_matrix قبل استدعاء الملاءمة ومصفوفة متفرقة csr_matrix قبل استدعاء التنبؤ. يمكن أن يكون وقت التدريب أسرع بعدة مرات لمصفوفة متفرقة مقارنة بمصفوفة كثيفة عندما تحتوي الميزات على قيم صفرية في معظم العينات.

1.10.6. خوارزميات الشجرة: ID3 وC4.5 وC5.0 وCART#

ما هي خوارزميات شجرة القرار المختلفة وكيف تختلف من بعضها البعض؟ أي منها يتم تنفيذه في scikit-learn؟

خوارزميات شجرة القرار المختلفة#

تم تطوير ID3 في عام 1986 بواسطة Ross Quinlan. تقوم الخوارزمية بإنشاء شجرة متعددة الطرق، حيث يتم العثور على الميزة الفئوية التي ستعطي أكبر مكسب للمعلومات للفئات المستهدفة الفئوية في كل عقدة (أي بطريقة جشعة). تنمو الأشجار إلى أقصى حجم لها، ثم يتم تطبيق خطوة التقليم عادةً لتحسين قدرة الشجرة على التعميم على البيانات غير المرئية.

C4.5 هي الخلف لـ ID3 وتزيل التقييد بأن الميزات

يجب أن تكون فئوية من خلال تعريف سمة منفصلة (بناءً على المتغيرات الرقمية) التي تقسم القيمة المستمرة للسمة إلى مجموعة من الفترات المنفصلة. يحول C4.5 الأشجار المدربة (أي ناتج خوارزمية ID3) إلى مجموعات من قواعد if-then. يتم تقييم دقة كل قاعدة ثم يتم تحديد الترتيب الذي يجب تطبيقه. يتم التقليم عن طريق إزالة شرط قاعدة ما إذا تحسنت الدقة بدونها.

C5.0 هو أحدث إصدار من Quinlan تم إصداره بموجب ترخيص ملكية.

يستخدم ذاكرة أقل ويبني مجموعات قواعد أصغر من C4.5 مع كونها أكثر دقة.

CART (شجرة التصنيف والانحدار) مشابه جدًا لـ C4.5، ولكنه يختلف في أنه يدعم المتغيرات المستهدفة الرقمية (الانحدار) ولا يحسب مجموعات القواعد. يقوم CART ببناء أشجار ثنائية باستخدام الميزة

والعتبة التي تعطي أكبر مكسب للمعلومات في كل عقدة.

يستخدم scikit-learn إصدارًا محسنًا من خوارزمية CART؛ ومع ذلك، فإن تنفيذ scikit-learn لا يدعم المتغيرات الفئوية في الوقت الحالي.

1.10.7. الصياغة الرياضية#

نظرًا لمتجهات التدريب \(x_i \in R^n\)، i=1,..., l ومجموعة تسميات \(y \in R^l\)، فإن شجرة القرار تقسم مساحة الميزات بشكل متكرر بحيث يتم تجميع العينات ذات التسميات نفسها أو قيم الهدف المتشابهة معًا.

دع البيانات في العقدة \(m\) يتم تمثيلها بواسطة \(Q_m\) مع \(n_m\) عينات. لكل حد مرشح \(\theta = (j, t_m)\) يتكون من ميزة \(j\) وعتبة \(t_m\)، قم بتقسيم البيانات إلى \(Q_m^{left}(\theta)\) و \(Q_m^{right}(\theta)\) المجموعات الفرعية

\[ \begin{align}\begin{aligned}Q_m^{left}(\theta) = \{(x, y) | x_j \leq t_m\}\\Q_m^{right}(\theta) = Q_m \setminus Q_m^{left}(\theta)\end{aligned}\end{align} \]

يتم حساب جودة حد مرشح للعقدة \(m\) باستخدام دالة عدم النقاء أو دالة الخسارة \(H()\)، والتي يعتمد اختيارها على المهمة التي يتم حلها (التصنيف أو الانحدار)

\[G(Q_m, \theta) = \frac{n_m^{left}}{n_m} H(Q_m^{left}(\theta)) + \frac{n_m^{right}}{n_m} H(Q_m^{right}(\theta))\]

حدد المعلمات التي تقلل من عدم النقاء

\[\theta^* = \operatorname{argmin}_\theta G(Q_m, \theta)\]

كرر العملية الفرعية لـ \(Q_m^{left}(\theta^*)\) و \(Q_m^{right}(\theta^*)\) حتى يتم الوصول إلى عمق أقصى مسموح به، \(n_m < \min_{samples}\) أو \(n_m = 1\).

1.10.7.1. معايير التصنيف#

إذا كان الهدف هو نتيجة تصنيف تتخذ القيم 0,1,...,K-1، للعقدة \(m\)، دع

\[p_{mk} = \frac{1}{n_m} \sum_{y \in Q_m} I(y = k)\]

نسبة ملاحظات الفئة k في العقدة \(m\). إذا كانت \(m\) عقدة نهائية، يتم تعيين predict_proba لهذه المنطقة إلى \(p_{mk\).

معايير عدم النقاء الشائعة هي التالية.

Gini:

\[H(Q_m) = \sum_k p_{mk} (1 - p_{mk})\]

Log Loss أو Entropy:

\[H(Q_m) = - \sum_k p_{mk} \log(p_{mk})\]
Entropy Shannon#

يحسب معيار Entropy نسبة Entropy Shannon للفئات الممكنة. يأخذ

تكرارات الفئات لبيانات التدريب التي وصلت إلى ورقة معينة \(m\) كاحتمالاتها. استخدام Entropy Shannon كمعيار لتقسيم عقدة الشجرة يعادل تقليل الخسارة اللوجستية (المعروفة أيضًا باسم الانتروبيا المتقاطعة وdeviation multinomial) بين التسميات الحقيقية \(y_i\) وتنبؤات الاحتمالية \(T_k(x_i)\) لنموذج الشجرة \(T\) للفئة \(k\).

لمعرفة ذلك، تذكر أولاً أن الخسارة اللوجستية لنموذج الشجرة \(T\) المحسوب على مجموعة بيانات \(D\) يتم تعريفه كما يلي:

\[\mathrm{LL}(D, T) = -\frac{1}{n} \sum_{(x_i, y_i) \in D} \sum_k I(y_i = k) \log(T_k(x_i))\]

حيث \(D\) هي مجموعة بيانات التدريب من \(n\) أزواج \((x_i, y_i)\).

في شجرة التصنيف، تكون احتمالات الفئة المتوقعة داخل عقد الأوراق ثابتة، أي: لكل \((x_i, y_i) \in Q_m\)، يكون لدينا: \(T_k(x_i) = p_{mk\) لكل فئة \(k\).

تسمح هذه الخاصية بإعادة كتابة \(\mathrm{LL}(D, T)\) كمجموع نسب Entropy Shannon المحسوبة لكل ورقة من \(T\) مرجحة بعدد بيانات التدريب التي وصلت إلى كل ورقة:

\[\mathrm{LL}(D, T) = \sum_{m \in T} \frac{n_m}{n} H(Q_m)\]

1.10.7.2. معايير الانحدار#

إذا كان الهدف هو قيمة مستمرة، فبالنسبة للعقدة \(m\)، تكون المعايير الشائعة للحد الأدنى كمعايير لتحديد المواقع للانقسامات المستقبلية هي متوسط الخطأ التربيعي (MSE أو خطأ L2)، وانحراف Poisson بالإضافة إلى متوسط الخطأ المطلق (MAE أو خطأ L1). يحدد كل من MSE وانحراف Poisson القيمة المتوقعة لعقد الأوراق إلى متوسط القيمة المكتسبة \(\bar{y}_m\) للعقدة بينما يحدد MAE القيمة المتوقعة لعقد الأوراق إلى الوسيط \(median(y)_m\).

متوسط الخطأ التربيعي:

\[ \begin{align}\begin{aligned}\bar{y}_m = \frac{1}{n_m} \sum_{y \in Q_m} y\\H(Q_m) = \frac{1}{n_m} \sum_{y \in Q_m} (y - \bar{y}_m)^2\end{aligned}\end{align} \]

انحراف Poisson:

\[H(Q_m) = \frac{2}{n_m} \sum_{y \in Q_m} (y \log\frac{y}{\bar{y}_m} - y + \bar{y}_m)\]

قد يكون تعيين criterion="poisson" خيارًا جيدًا إذا كان هدفك هو عدد أو تكرار (عدد لكل وحدة). في أي حال، \(y >= 0\) هو شرط ضروري لاستخدام هذا المعيار. لاحظ أنه يتناسب بشكل أبطأ بكثير من معيار MSE. لأسباب تتعلق بالأداء، فإن التنفيذ الفعلي يقلل نصف انحراف Poisson، أي انحراف Poisson مقسومًا على 2.

متوسط الخطأ المطلق:

\[ \begin{align}\begin{aligned}median(y)_m = \underset{y \in Q_m}{\mathrm{median}}(y)\\H(Q_m) = \frac{1}{n_m} \sum_{y \in Q_m} |y - median(y)_m|\end{aligned}\end{align} \]

لاحظ أنه يتناسب بشكل أبطأ بكثير من معيار MSE.

1.10.8. دعم القيم المفقودة#

DecisionTreeClassifier، DecisionTreeRegressor تدعم القيم المفقودة المضمنة باستخدام splitter='best'، حيث يتم تحديد الانقسامات بطريقة جشعة. ExtraTreeClassifier، و ExtraTreeRegressor تدعم القيم المفقودة المضمنة لـ splitter='random'، حيث يتم تحديد الانقسامات عشوائيًا. لمزيد من التفاصيل حول كيفية اختلاف القاسم على القيم غير المفقودة، راجع قسم Forest.

المعايير المدعومة عند وجود قيم مفقودة هي 'gini'، 'entropy'، أو 'log_loss'، للتصنيف أو 'squared_error'، 'friedman_mse'، أو 'poisson' للانحدار.

أولاً، سنصف كيفية تعامل DecisionTreeClassifier، DecisionTreeRegressor مع القيم المفقودة في البيانات.

بالنسبة لكل عتبة محتملة على البيانات غير المفقودة، سيقوم القاسم بتقييم الانقسام مع ذهاب جميع القيم المفقودة إلى العقدة اليسرى أو العقدة اليمنى.

يتم اتخاذ القرارات على النحو التالي:

  • بشكل افتراضي عند التنبؤ، يتم تصنيف العينات ذات القيم المفقودة باستخدام الفئة المستخدمة في الانقسام الموجود أثناء التدريب:

    >>> from sklearn.tree import DecisionTreeClassifier
>>> import numpy as np

>>> X = np.array([0, 1, 6, np.nan]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]

>>> tree = DecisionTreeClassifier(random_state=0).fit(X, y)
>>> tree.predict(X)
array([0, 0, 1, 1])

  • إذا كان تقييم المعيار متساويًا لكلا العقدتين، فإن التعادل للقيمة المفقودة عند وقت التنبؤ يتم كسره بالذهاب إلى العقدة اليمنى. يتحقق القاسم أيضًا من الانقسام حيث تذهب جميع القيم المفقودة إلى طفل واحد والقيم غير المفقودة تذهب إلى الطفل الآخر:

    >>> from sklearn.tree import DecisionTreeClassifier
>>> import numpy as np

>>> X = np.array([np.nan, -1, np.nan, 1]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]

>>> tree = DecisionTreeClassifier(random_state=0).fit(X, y)

>>> X_test = np.array([np.nan]).reshape(-1, 1)
>>> tree.predict(X_test)
array([1])

  • إذا لم يتم رؤية أي قيم مفقودة أثناء التدريب لميزة معينة، فخلال التنبؤ يتم تعيين القيم المفقودة إلى الطفل الذي يحتوي على معظم العينات:

    >>> from sklearn.tree import DecisionTreeClassifier
>>> import numpy as np

>>> X = np.array([0, 1, 2, 3]).reshape(-1, 1)
>>> y = [0, 1, 1, 1]

>>> tree = DecisionTreeClassifier(random_state=0).fit(X, y)

>>> X_test = np.array([np.nan]).reshape(-1, 1)
>>> tree.predict(X_test)
array([1])

ExtraTreeClassifier، و ExtraTreeRegressor تتعامل مع القيم المفقودة بطريقة مختلفة قليلاً. عند تقسيم عقدة، سيتم اختيار عتبة عشوائية للتقسيم على القيم غير المفقودة. بعد ذلك، سيتم إرسال القيم غير المفقودة إلى الطفل الأيسر واليمين بناءً على العتبة العشوائية المختارة، بينما سيتم إرسال القيم المفقودة عشوائيًا إلى الطفل الأيسر أو الأيمن. يتم تكرار هذا لكل ميزة يتم النظر فيها في كل انقسام. يتم اختيار أفضل انقسام من بين هذه الانقسامات.

أثناء التنبؤ، يكون التعامل مع القيم المفقودة هو نفسه كما هو الحال في شجرة القرار:

  • بشكل افتراضي عند التنبؤ، يتم تصنيف العينات ذات القيم المفقودة باستخدام الفئة المستخدمة في الانقسام الموجود أثناء التدريب.

  • إذا لم يتم رؤية أي قيم مفقودة أثناء التدريب لميزة معينة، فخلال التنبؤ يتم تعيين القيم المفقودة إلى الطفل الذي يحتوي على معظم العينات.

1.10.9. التقليم الأدنى لتكلفة التعقيد#

التقليم الأدنى لتكلفة التعقيد هو خوارزمية مستخدمة لتقليم شجرة لتجنب الإفراط في الملاءمة، موصوفة في الفصل 3 من [BRE]. هذه الخوارزمية معلمة بـ \(\alpha\ge0\) المعروف باسم معامل التعقيد. يتم استخدام معامل التعقيد لتعريف مقياس تكلفة التعقيد، \(R_\alpha(T)\) لشجرة معينة \(T\):

\[R_\alpha(T) = R(T) + \alpha|\widetilde{T}|\]

حيث \(|\widetilde{T}|\) هو عدد العقد النهائية في \(T\) و \(R(T)\) عادة ما يتم تعريفه على أنه معدل الخطأ الإجمالي لعقد الأوراق. بدلاً من ذلك، يستخدم scikit-learn مجموع عدم النقاء المرجح للعينات للعقد النهائية لـ \(R(T)\). كما هو موضح أعلاه، يعتمد عدم النقاء للعقدة على المعيار. يجد التقليم الأدنى لتكلفة التعقيد الشجرة الفرعية لـ \(T\) التي تقلل \(R_\alpha(T)\).

مقياس تكلفة التعقيد لعقدة واحدة هو \(R_\alpha(t)=R(t)+\alpha\). الفرع، \(T_t\)، هو شجرة حيث العقدة \(t\) هي جذرها. بشكل عام، يكون عدم نقاء العقدة أكبر من مجموع عدم نقاء عقد أوراقها، \(R(T_t)<R(t)\). ومع ذلك، يمكن أن يكون مقياس تكلفة التعقيد للعقدة، \(t\)، وفرعها، \(T_t\)، متساويًا اعتمادًا على \(\alpha\). نحن نحدد \(\alpha\) الفعال للعقدة على أنه القيمة التي يكونان فيها متساويين، \(R_\alpha(T_t)=R_\alpha(t)\) أو \(\alpha_{eff}(t)=\frac{R(t)-R(T_t)}{|T|-1}\). العقدة غير النهائية ذات القيمة الأصغر من \(\alpha_{eff}\) هي الحلقة الأضعف وسيتم تقليمها. تتوقف هذه العملية عندما يكون \(\alpha_{eff}\) الأدنى للشجرة المقلمة أكبر من معلمة ccp_alpha.

أمثلة

المراجع

[BRE]

L. Breiman, J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Wadsworth, Belmont, CA, 1984.