2.1. نماذج خليط غاوسي#

sklearn.mixture هي حزمة تُمكّن المرء من تعلم نماذج خليط غاوسي (يتم دعم مصفوفات التغاير القُطرية، الكروية، المُقيّدة، والتامة)، وأخذ عينات منها، وتقديرها من البيانات. يتم أيضًا توفير التسهيلات للمساعدة في تحديد العدد المناسب من المكونات.

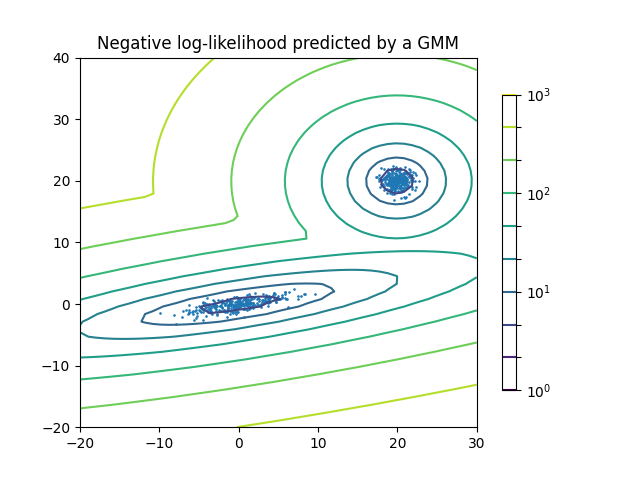
../_images/sphx_glr_plot_gmm_pdf_001.png

نموذج خليط غاوسي ثنائي المكونات: نقاط البيانات، وأسطح احتمالية متساوية للنموذج.#

نموذج خليط غاوسي هو نموذج احتمالي يفترض أن جميع نقاط البيانات يتم إنشاؤها من خليط من عدد محدود من توزيعات غاوسي ذات معلمات غير معروفة. يمكن للمرء أن يفكر في نماذج الخليط على أنها تعميم لتجميع k-means لدمج معلومات حول بنية التغاير للبيانات بالإضافة إلى مراكز توزيعات غاوسي الكامنة.

تُطبق Scikit-learn فئات مختلفة لتقدير نماذج خليط غاوسي، والتي تتوافق مع استراتيجيات تقدير مختلفة، مفصلة أدناه.

2.1.1. خليط غاوسي#

يُطبق الكائن GaussianMixture خوارزمية التوقع-التعظيم (EM) لملاءمة نماذج خليط غاوسي. يمكنه أيضًا رسم أشكال بيضاوية ثقة للنماذج متعددة المتغيرات، وحساب معيار معلومات بايز لتقييم عدد المجموعات في البيانات. يتم توفير طريقة GaussianMixture.fit التي تتعلم نموذج خليط غاوسي من بيانات التدريب. بالنظر إلى بيانات الاختبار، يمكنها تعيين توزيع غاوسي الذي من المرجح أن تنتمي إليه كل عينة باستخدام الطريقة GaussianMixture.predict.

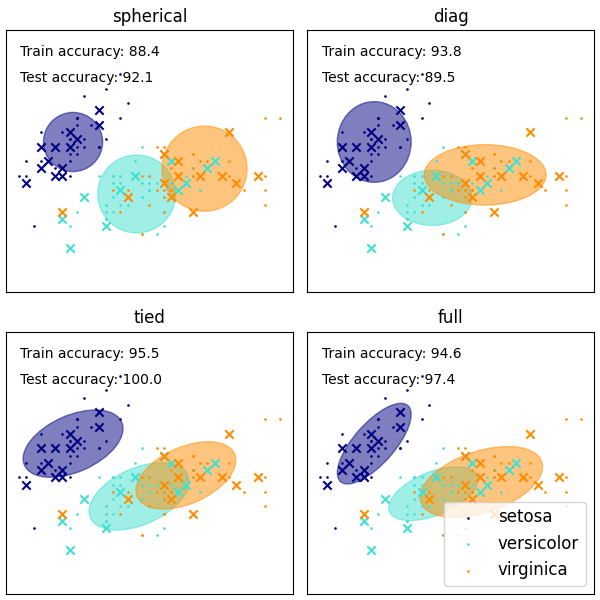
يأتي GaussianMixture مع خيارات مختلفة لتقييد التغاير لفرق الفئات المُقدّرة: التغاير الكروي، أو القطري، أو المُقيّد، أو التام.

../_images/sphx_glr_plot_gmm_covariances_001.png

أمثلة

إيجابيات وسلبيات الفئة GaussianMixture#

الإيجابيات

السرعة:

إنها أسرع خوارزمية لتعلم نماذج الخليط

لا مُعَرِّف:

نظرًا لأن هذه الخوارزمية تُعظّم الاحتمالية فقط، فإنها لن تُحيز الوسائل نحو الصفر، أو تُحيز أحجام الكتلة لتكوين بنى مُحدّدة قد تنطبق أو لا تنطبق.

السلبيات

الفرادات:

عندما يكون لدى المرء عدد غير كافٍ من النقاط لكل خليط، يصبح تقدير مصفوفات التغاير أمرًا صعبًا، ومن المعروف أن الخوارزمية تتباعد وتجد حلولًا ذات احتمالية غير محدودة ما لم ينظم المرء التغايرات بشكل مصطنع.

عدد المكونات:

ستستخدم هذه الخوارزمية دائمًا جميع المكونات التي يمكنها الوصول إليها، وتحتاج إلى بيانات مُستبعدة أو معايير معلومات نظرية لتحديد عدد المكونات التي يجب استخدامها في حالة عدم وجود إشارات خارجية.

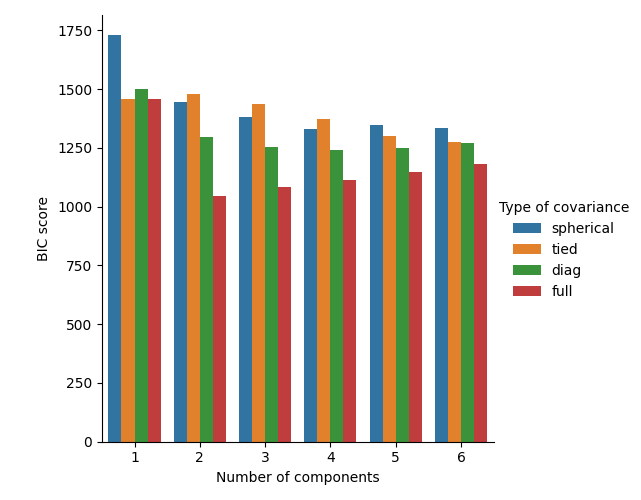
تحديد عدد المكونات في نموذج خليط غاوسي الكلاسيكي#

يمكن استخدام معيار BIC لتحديد عدد المكونات في خليط غاوسي بطريقة فعالة. من الناحية النظرية، فإنه يستعيد العدد الحقيقي للمكونات فقط في النظام المقارب (أي إذا كان هناك الكثير من البيانات المتاحة بافتراض أن البيانات تم إنشاؤها بالفعل بشكل مستقل ومتماثل من خليط من توزيع غاوسي). لاحظ أن استخدام خليط غاوسي بايزي المتغير يتجنب تحديد عدد المكونات لنموذج خليط غاوسي.

../_images/sphx_glr_plot_gmm_selection_002.png

أمثلة

خوارزمية التقدير: التوقع-التعظيم#

الصعوبة الرئيسية في تعلم نماذج خليط غاوسي من البيانات غير المُعلمة هي أن المرء لا يعرف عادةً النقاط التي جاءت من أي مكون كامن (إذا كان لدى المرء إمكانية الوصول إلى هذه المعلومات، يصبح من السهل جدًا ملاءمة توزيع غاوسي منفصل لكل مجموعة من النقاط). التوقع-التعظيم هي خوارزمية إحصائية راسخة للتغلب على هذه المشكلة من خلال عملية تكرارية. أولاً، يفترض المرء مكونات عشوائية (مركزة عشوائيًا على نقاط البيانات، متعلمة من k-means، أو حتى موزعة بشكل طبيعي حول الأصل) ويحسب لكل نقطة احتمال توليدها بواسطة كل مكون من مكونات النموذج. بعد ذلك، يقوم المرء بضبط المعلمات لتعظيم احتمالية البيانات بالنظر إلى هذه التعيينات. من المضمون أن تؤدي تكرار هذه العملية دائمًا إلى الوصول إلى حد أقصى محلي.

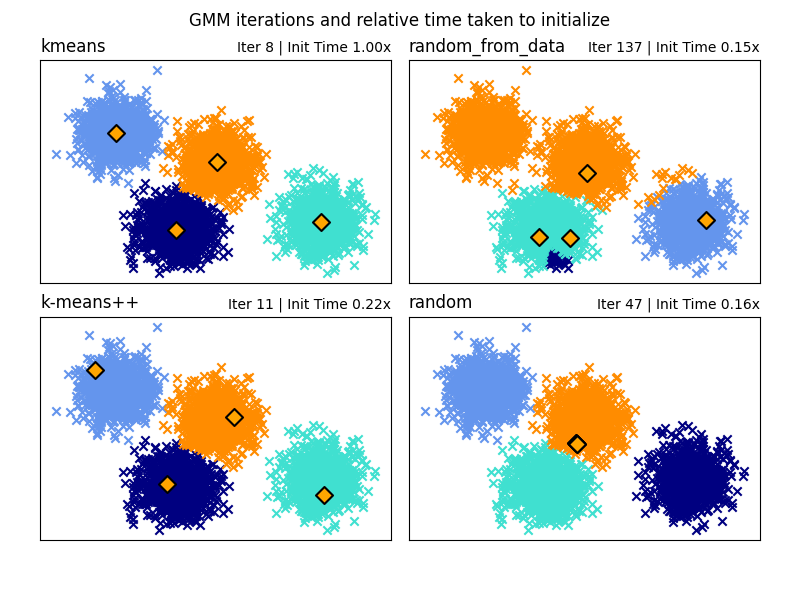
اختيار طريقة التهيئة#

هناك خيار من أربع طرق تهيئة (بالإضافة إلى إدخال وسائل أولية مُحدّدة من قبل المستخدم) لإنشاء المراكز الأولية لمكونات النموذج:

k-means (افتراضي)

يطبق هذا خوارزمية تجميع k-means التقليدية. يمكن أن يكون هذا مكلفًا من الناحية الحسابية مقارنة بطرق التهيئة الأخرى.

k-means++

يستخدم هذا طريقة التهيئة لتجميع k-means: k-means++. سيختار هذا المركز الأول عشوائيًا من البيانات. سيتم اختيار المراكز اللاحقة من توزيع مرجح للبيانات يُفضّل النقاط الأبعد عن المراكز الحالية. k-means++ هو التهيئة الافتراضية لـ k-means، لذا سيكون أسرع من تشغيل k-means كامل، ولكنه قد يستغرق قدرًا كبيرًا من الوقت لمجموعات البيانات الكبيرة ذات المكونات الكثيرة.

random_from_data

سيختار هذا نقاط بيانات عشوائية من بيانات الإدخال كمراكز أولية. هذه طريقة سريعة جدًا للتهيئة ولكنها قد تُنتج نتائج غير متقاربة إذا كانت النقاط المُختارة قريبة جدًا من بعضها البعض.

random

يتم اختيار المراكز كاضطراب صغير بعيدًا عن متوسط جميع البيانات. هذه الطريقة بسيطة ولكنها قد تؤدي إلى استغراق النموذج وقتًا أطول للتقارب.

../_images/sphx_glr_plot_gmm_init_001.png

أمثلة

2.1.2. خليط غاوسي بايزي المتغير#

يُطبق الكائن BayesianGaussianMixture متغيرًا من نموذج خليط غاوسي مع خوارزميات الاستدلال المتغيرة. واجهة برمجة التطبيقات تشبه تلك المُحدّدة بواسطة GaussianMixture.

خوارزمية التقدير: الاستدلال المتغير

الاستدلال المتغير هو امتداد للتوقع-التعظيم الذي يُعظّم الحد الأدنى على دليل النموذج (بما في ذلك التوزيعات المسبقة) بدلاً من احتمالية البيانات. المبدأ وراء الطرق المتغيرة هو نفس التوقع-التعظيم (أي أن كلاهما خوارزميات تكرارية تتناوب بين إيجاد الاحتمالات لكل نقطة ليتم إنشاؤها بواسطة كل خليط وملاءمة الخليط لهذه النقاط المعينة)، لكن الطرق المتغيرة تضيف التنظيم عن طريق دمج المعلومات من التوزيعات المسبقة. هذا يتجنب الفرادات التي توجد غالبًا في حلول التوقع-التعظيم ولكنه يُدخل بعض التحيزات الدقيقة للنموذج. غالبًا ما يكون الاستدلال أبطأ بشكل ملحوظ، ولكن ليس عادةً بقدر ما يجعل الاستخدام غير عملي.

نظرًا لطبيعته البايزية، تحتاج الخوارزمية المتغيرة إلى معلمات فائقة أكثر من التوقع-التعظيم، وأهمها معلمة التركيز weight_concentration_prior. سيؤدي تحديد قيمة منخفضة للتركيز المسبق إلى جعل النموذج يضع معظم الوزن على عدد قليل من المكونات ويُعيّن أوزان المكونات المتبقية قريبة جدًا من الصفر. ستسمح القيم العالية للتركيز المسبق لعدد أكبر من المكونات أن تكون نشطة في الخليط.

يقترح تنفيذ المعلمات للفئة BayesianGaussianMixture نوعين من التوزيع المسبق لتوزيع الأوزان: نموذج خليط محدود مع توزيع ديريتشليت ونموذج خليط لانهائي مع عملية ديريتشليت. في الممارسة العملية، يتم تقريب خوارزمية استدلال عملية ديريتشليت وتستخدم توزيعًا مبتورًا مع عدد أقصى ثابت من المكونات (يسمى تمثيل كسر العصا). يعتمد عدد المكونات المستخدمة فعليًا دائمًا تقريبًا على البيانات.

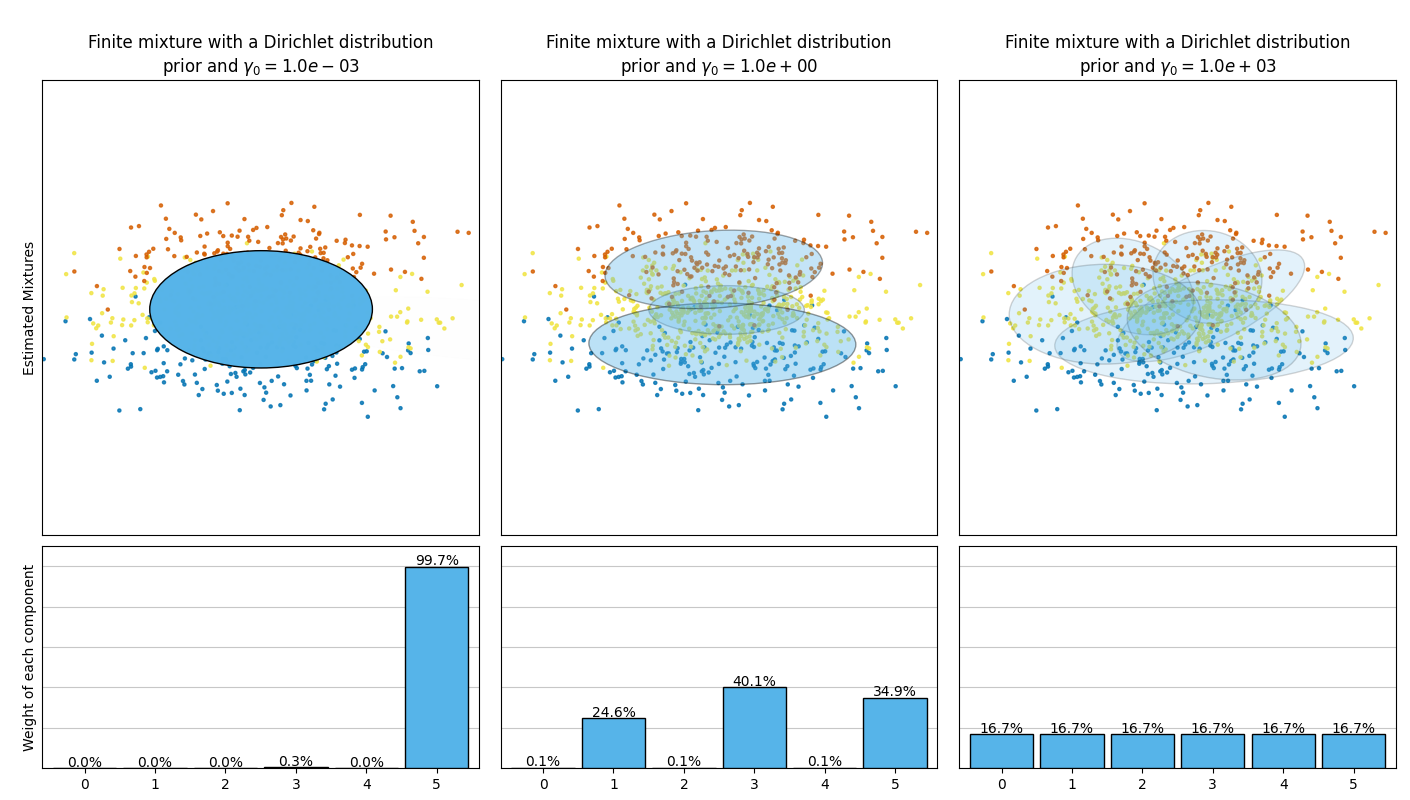
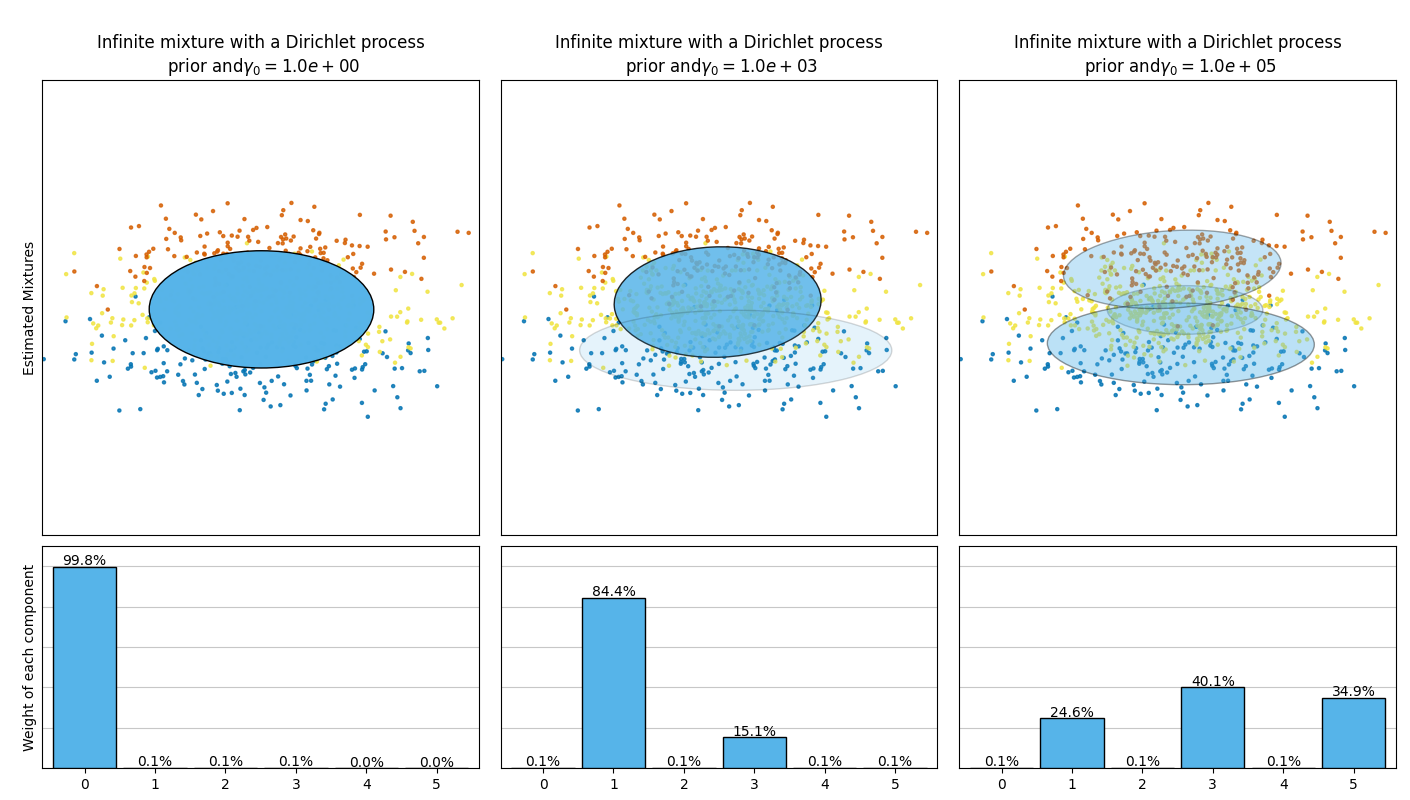
تقارن الصورة التالية النتائج التي تم الحصول عليها للنوع المختلف من التركيز المسبق للوزن (المعلمة weight_concentration_prior_type) لقيم مختلفة من weight_concentration_prior. هنا، يمكننا أن نرى أن قيمة المعلمة weight_concentration_prior لها تأثير قوي على العدد الفعال للمكونات النشطة التي تم الحصول عليها. يمكننا أيضًا ملاحظة أن القيم الكبيرة للتركيز المسبق للوزن تؤدي إلى أوزان أكثر اتساقًا عندما يكون نوع التوزيع المسبق هو "dirichlet_distribution" بينما لا يكون هذا هو الحال بالضرورة بالنسبة للنوع "dirichlet_process" (المستخدم افتراضيًا).

plot_bgmm plot_dpgmm

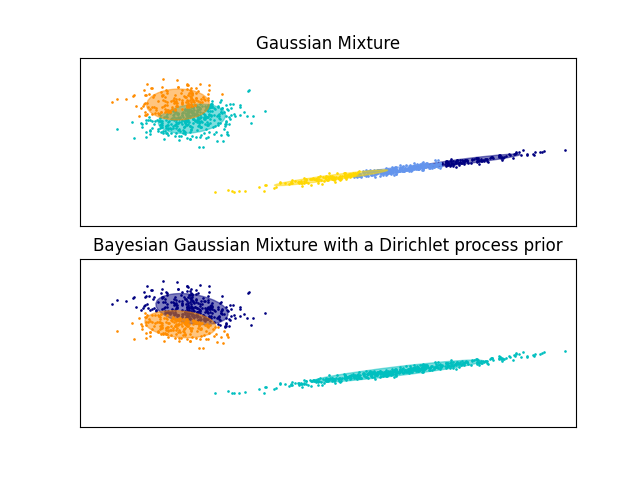
تُقارن الأمثلة أدناه نماذج خليط غاوسي مع عدد ثابت من المكونات، بنماذج خليط غاوسي المتغيرة مع توزيع مسبق لعملية ديريتشليت. هنا، يتم ملاءمة خليط غاوسي كلاسيكي مع 5 مكونات على مجموعة بيانات تتكون من مجموعتين. يمكننا أن نرى أن خليط غاوسي المتغير مع توزيع مسبق لعملية ديريتشليت قادر على قصر نفسه على مكونين فقط بينما يُناسب خليط غاوسي البيانات مع عدد ثابت من المكونات التي يجب ضبطها مسبقًا بواسطة المستخدم. في هذه الحالة، اختار المستخدم n_components=5 وهو ما لا يتطابق مع التوزيع التوليدي الحقيقي لمجموعة بيانات الألعاب هذه. لاحظ أنه مع عدد قليل جدًا من الملاحظات، يمكن أن تتخذ نماذج خليط غاوسي المتغيرة ذات التوزيع المسبق لعملية ديريتشليت موقفًا مُحافظًا، وتناسب مكونًا واحدًا فقط.

../_images/sphx_glr_plot_gmm_001.png

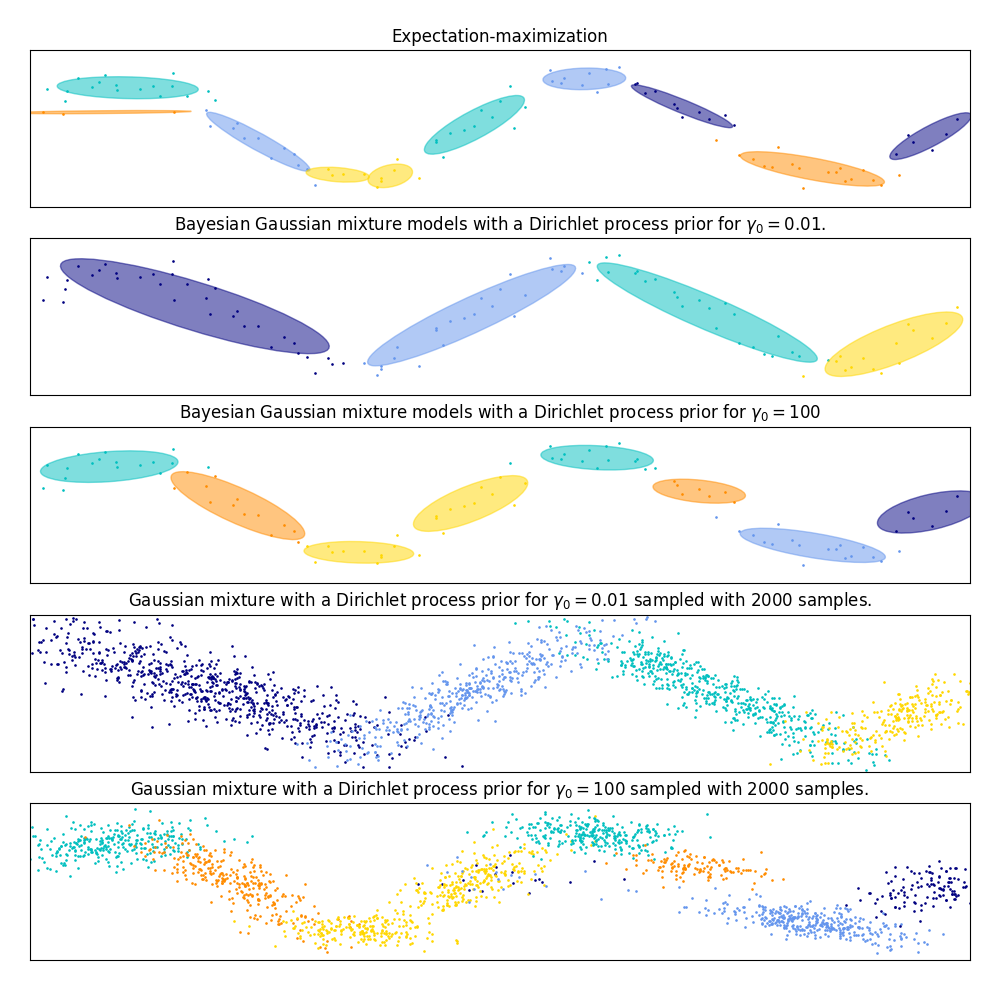
في الشكل التالي، نُناسب مجموعة بيانات لا يتم تصويرها جيدًا بواسطة خليط غاوسي. ضبط المعلمة weight_concentration_prior لـ BayesianGaussianMixture يتحكم في عدد المكونات المستخدمة لملاءمة هذه البيانات. نُقدّم أيضًا في الرسمين الأخيرين عينة عشوائية تم إنشاؤها من الخليطين الناتجين.

../_images/sphx_glr_plot_gmm_sin_001.png

أمثلة

إيجابيات وسلبيات الاستدلال المتغير مع BayesianGaussianMixture#

الإيجابيات

الاختيار التلقائي:

عندما يكون weight_concentration_prior صغيرًا بما يكفي و n_components أكبر مما يراه النموذج ضروريًا، فإن نموذج خليط بايز المتغير لديه ميل طبيعي لتعيين بعض قيم أوزان الخليط قريبة من الصفر. وهذا يجعل من الممكن أن يختار النموذج عددًا مناسبًا من المكونات الفعالة تلقائيًا. يلزم فقط توفير حد أعلى لهذا الرقم. لاحظ مع ذلك أن العدد "المثالي" للمكونات النشطة مُحدّد جدًا للتطبيق وعادةً ما يكون غير مُحدّد جيدًا في إعداد استكشاف البيانات.

حساسية أقل لعدد المعلمات:

على عكس النماذج المحدودة، والتي ستستخدم دائمًا جميع المكونات بقدر ما تستطيع، وبالتالي ستنتج حلولًا مختلفة تمامًا لأعداد مختلفة من المكونات، فإن الاستدلال المتغير مع توزيع مسبق لعملية ديريتشليت (weight_concentration_prior_type='dirichlet_process') لن يتغير كثيرًا مع تغييرات المعلمات، مما يؤدي إلى مزيد من الاستقرار وضبط أقل.

التنظيم:

نظرًا لدمج المعلومات المسبقة، فإن الحلول المتغيرة لديها حالات خاصة أقل مرضية من حلول التوقع-التعظيم.

السلبيات

السرعة:

المعلمات الإضافية اللازمة للاستدلال المتغير تجعل الاستدلال أبطأ، وإن لم يكن كثيرًا.

المعلمات الفائقة:

تحتاج هذه الخوارزمية إلى معلمة فائقة إضافية قد تتطلب ضبطًا تجريبيًا عبر التحقق المتبادل.

الانحياز:

هناك العديد من التحيزات الضمنية في خوارزميات الاستدلال (وأيضًا في عملية ديريتشليت إذا تم استخدامها)، وكلما كان هناك عدم تطابق بين هذه التحيزات والبيانات، فقد يكون من الممكن ملاءمة نماذج أفضل باستخدام خليط محدود.

2.1.2.1. عملية ديريتشليت - The Dirichlet Process#

نصف هنا خوارزميات الاستدلال المتغيرة في خليط عملية ديريتشليت. عملية ديريتشليت هي توزيع احتمالي مسبق على التجميعات ذات عدد غير محدود من الأقسام. تسمح لنا التقنيات المتغيرة بدمج هذه البنية المسبقة على نماذج خليط غاوسي مع عدم وجود عقوبة تقريبًا في وقت الاستدلال، مقارنةً بنموذج خليط غاوسي محدود.

السؤال المهم هو كيف يمكن لعملية ديريتشليت استخدام عدد غير محدود من المجموعات ولا تزال متسقة. بينما لا يتناسب التفسير الكامل مع هذا الدليل، يمكن للمرء أن يفكر في تشبيه عملية كسر العصا للمساعدة في فهمها. عملية كسر العصا هي قصة توليدية لعملية ديريتشليت. نبدأ بعصا بطول الوحدة وفي كل خطوة نكسر جزءًا من العصا المتبقية. في كل مرة، نربط طول قطعة العصا بنسبة النقاط التي تقع في مجموعة من الخليط. في النهاية، لتمثيل الخليط اللانهائي، نربط قطعة العصا المتبقية الأخيرة بنسبة النقاط التي لا تقع في جميع المجموعات الأخرى. طول كل قطعة هو متغير عشوائي مع احتمال يتناسب مع معلمة التركيز. ستقسم القيم الأصغر للتركيز طول الوحدة إلى قطع أكبر من العصا (تحديد توزيع أكثر تركيزًا). ستنشئ قيم التركيز الأكبر قطعًا أصغر من العصا (زيادة عدد المكونات ذات الأوزان غير الصفرية).

لا تزال تقنيات الاستدلال المتغيرة لعملية ديريتشليت تعمل مع تقريب محدود لنموذج الخليط اللانهائي هذا، ولكن بدلاً من الاضطرار إلى تحديد عدد المكونات التي يريد المرء استخدامها مسبقًا، يُحدّد المرء فقط معلمة التركيز والحد الأعلى لعدد مكونات الخليط (هذا الحد الأعلى، بافتراض أنه أعلى من العدد "الحقيقي" للمكونات، يؤثر فقط على التعقيد الخوارزمي، وليس العدد الفعلي للمكونات المستخدمة).