6.3. المعالجة المسبقة للبيانات#
تُوفر حزمة sklearn.preprocessing العديد من وظائف الأداة المساعدة وفئات المحولات الشائعة لتغيير متجهات الميزات الأولية إلى تمثيل أكثر ملاءمة لمقدرات المراحل اللاحقة.
بشكل عام، تستفيد العديد من خوارزميات التعلم مثل النماذج الخطية من توحيد مجموعة البيانات (انظر أهمية معايرة الميزات). إذا كانت بعض القيم المتطرفة موجودة في المجموعة، فقد تكون أدوات التحجيم(قياس) القوية أو المحولات الأخرى أكثر ملاءمة. يتم تمييز سلوكيات أدوات التحجيم(قياس) والمحولات والمعيّرات المختلفة على مجموعة بيانات تحتوي على قيم متطرفة هامشية في مقارنة تأثير المقياس المختلف على البيانات مع القيم الشاذة.
6.3.1. التوحيد التحجيم(قياس)ي، أو إزالة المتوسط وتحجيم(قياس) التباين#
توحيد مجموعات البيانات هو شرط شائع للعديد من مقدرات تعلم الآلة المُطبقة في scikit-learn؛ قد تُسيء التصرف إذا لم تكن الميزات الفردية تُشبه إلى حد ما البيانات الموزعة بشكل طبيعي تحجيم(قياس)ي: غاوسي بـ متوسط صفر وتباين وحدة.
في الممارسة العملية، غالبًا ما نتجاهل شكل التوزيع ونقوم فقط بتحويل البيانات لتركيزها عن طريق إزالة متوسط قيمة كل ميزة، ثم تحجيم(قياس)ها عن طريق قسمة الميزات غير الثابتة على انحرافها المعياري.
على سبيل المثال، قد تفترض العديد من العناصر المستخدمة في دالة الهدف لخوارزمية التعلم (مثل نواة RBF لآلات متجه الدعم أو معيّنات l1 و l2 للنماذج الخطية) أن جميع الميزات مركزة حول الصفر أو أن التباين بنفس الترتيب. إذا كانت الميزة تحتوي على تباين أكبر من غيرها بأوامر من حيث الحجم، فقد تُهيمن على دالة الهدف وتجعل المقدّر غير قادر على التعلم من الميزات الأخرى بشكل صحيح كما هو متوقع.
تُوفر الوحدة preprocessing فئة الأداة المساعدة StandardScaler، وهي طريقة سريعة وسهلة لإجراء العملية التالية على مجموعة بيانات تُشبه المصفوفة:
>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> scaler
StandardScaler()
>>> scaler.mean_
array([1. ..., 0. ..., 0.33...])
>>> scaler.scale_
array([0.81..., 0.81..., 1.24...])
>>> X_scaled = scaler.transform(X_train)
>>> X_scaled
array([[ 0. ..., -1.22..., 1.33...],
[ 1.22..., 0. ..., -0.26...],
[-1.22..., 1.22..., -1.06...]])
البيانات المُقاسة لها متوسط صفر وتباين وحدة:
>>> X_scaled.mean(axis=0)
array([0., 0., 0.])
>>> X_scaled.std(axis=0)
array([1., 1., 1.])
تُطبق هذه الفئة واجهة برمجة تطبيقات Transformer لحساب المتوسط والانحراف المعياري على مجموعة التدريب بحيث تكون قادرة على إعادة تطبيق نفس التحويل على مجموعة الاختبار لاحقًا. وبالتالي، فإن هذه الفئة مُناسبة للاستخدام في الخطوات الأولى من Pipeline:
>>> from sklearn.datasets import make_classification
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> X, y = make_classification(random_state=42)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
>>> pipe = make_pipeline(StandardScaler(), LogisticRegression())
>>> pipe.fit(X_train, y_train) # تطبيق التحجيم(قياس) على بيانات التدريب
Pipeline(steps=[('standardscaler', StandardScaler()),
('logisticregression', LogisticRegression())])
>>> pipe.score(X_test, y_test) # تطبيق التحجيم(قياس) على بيانات الاختبار، دون تسريب بيانات التدريب.
0.96
من الممكن تعطيل إما التركيز أو التحجيم(قياس) عن طريق تمرير with_mean=False أو with_std=False إلى مُنشئ StandardScaler.
6.3.1.1. تحجيم الميزات إلى نطاق#
التوحيد التحجيم(قياس)ي البديل هو تحجيم(قياس) الميزات لتقع بين قيمة دنيا وقيمة عظمى مُعطاة، غالبًا بين الصفر والواحد، أو بحيث يتم تحجيم(قياس) القيمة المطلقة القصوى لكل ميزة إلى حجم الوحدة. يمكن تحقيق ذلك باستخدام MinMaxScaler أو MaxAbsScaler، على التوالي.
يتضمن الدافع لاستخدام هذا التحجيم(قياس) المتانة للانحرافات المعيارية الصغيرة جدًا للميزات والحفاظ على إدخالات صفرية في البيانات المتفرقة.
فيما يلي مثال لتحجيم(قياس) مصفوفة بيانات تجريبية إلى النطاق [0, 1]:
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[0.5 , 0. , 1. ],
[1. , 0.5 , 0.33333333],
[0. , 1. , 0. ]])
يمكن بعد ذلك تطبيق نفس مثيل المحول على بعض بيانات الاختبار الجديدة غير المرئية أثناء استدعاء الملاءمة: سيتم تطبيق نفس عمليات التحجيم(قياس) والإزاحة لتكون متسقة مع التحويل الذي تم إجراؤه على بيانات التدريب:
>>> X_test = np.array([[-3., -1., 4.]])
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5 , 0. , 1.66666667]])
من الممكن فحص سمات أداة التحجيم(قياس) لمعرفة الطبيعة الدقيقة للتحويل الذي تم تعلمه على بيانات التدريب:
>>> min_max_scaler.scale_
array([0.5 , 0.5 , 0.33...])
>>> min_max_scaler.min_
array([0. , 0.5 , 0.33...])
إذا تم إعطاء MinMaxScaler feature_range=(min, max) صريحة، فإن الصيغة الكاملة هي:
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
تعمل MaxAbsScaler بطريقة مشابهة جدًا، ولكنها تقيس بطريقة تجعل بيانات التدريب تقع ضمن النطاق [-1, 1] عن طريق القسمة على أكبر قيمة عظمى في كل ميزة. وهي مخصصة للبيانات التي تم تركيزها بالفعل عند الصفر أو البيانات المتفرقة.
فيما يلي كيفية استخدام بيانات الألعاب من المثال السابق مع أداة التحجيم(قياس) هذه:
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
...
>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. , 1. ],
[ 1. , 0. , 0. ],
[ 0. , 1. , -0.5]])
>>> X_test = np.array([[ -3., -1., 4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. , 2. ]])
>>> max_abs_scaler.scale_
array([2., 1., 2.])
6.3.1.2. تحجيم(قياس) البيانات المتفرقة#
سيؤدي تركيز البيانات المتفرقة إلى تدمير بنية التفرق في البيانات، وبالتالي نادرًا ما يكون شيئًا معقولًا للقيام به. ومع ذلك، قد يكون من المنطقي تحجيم(قياس) المدخلات المتفرقة، خاصةً إذا كانت الميزات على مقاييس مختلفة.
تم تصميم MaxAbsScaler خصيصًا لتحجيم(قياس) البيانات المتفرقة، وهي الطريقة المُوصى بها للقيام بذلك. ومع ذلك، يمكن لـ StandardScaler قبول مصفوفات scipy.sparse كمدخلات، طالما تم تمرير with_mean=False بشكل صريح إلى المُنشئ. وإلا، فسيتم طرح ValueError حيث أن التركيز الصامت سيُفسد التفرق وغالبًا ما يُعطّل التنفيذ عن طريق تخصيص كميات زائدة من الذاكرة عن غير قصد. لا يمكن ملاءمة RobustScaler مع المدخلات المتفرقة، ولكن يمكنك استخدام طريقة transform على المدخلات المتفرقة.
لاحظ أن أدوات التحجيم(قياس) تقبل كل من تنسيق صفوف متفرقة مضغوطة وأعمدة متفرقة مضغوطة (انظر scipy.sparse.csr_matrix و scipy.sparse.csc_matrix). سيتم تحويل أي إدخال متفرق آخر إلى تمثيل صفوف متفرقة مضغوطة. لتجنب نسخ الذاكرة غير الضرورية، يُوصى باختيار تمثيل CSR أو CSC في المراحل السابقة.
أخيرًا، إذا كان من المتوقع أن تكون البيانات المركزة صغيرة بما يكفي، فإن تحويل الإدخال بشكل صريح إلى مصفوفة باستخدام طريقة toarray للمصفوفات المتفرقة هو خيار آخر.
6.3.1.3. تحجيم(قياس) البيانات مع القيم المتطرفة#
إذا كانت بياناتك تحتوي على العديد من القيم المتطرفة، فمن المُرجّح ألا يعمل التحجيم(قياس) باستخدام المتوسط والتباين للبيانات بشكل جيد للغاية. في هذه الحالات، يمكنك استخدام RobustScaler كبديل مباشر. تستخدم تقديرات أكثر قوة للمركز ونطاق بياناتك.
المراجع#
مناقشة أخرى حول أهمية تركيز البيانات وتحجيم(قياس)ها متاحة في هذه الأسئلة الشائعة: هل يجب عليّ تطبيع/توحيد/إعادة تحجيم(قياس) البيانات؟
6.3.1.4. تمركز النواة أو تجانس النواة - Kernal centering#
إذا كان لديك مصفوفة نواة من نواة \(K\) تقوم بحساب حاصل الضرب النقطي في فضاء الميزات (ربما بشكل ضمني) مُحدّد بواسطة دالة \(\phi(\cdot)\)، فيمكن لـ KernelCenterer تحويل مصفوفة النواة بحيث تحتوي على حاصل الضرب الداخلي في فضاء الميزات المُحدّد بواسطة \(\phi\) متبوعًا بإزالة المتوسط في تلك المساحة. بعبارة أخرى، تحسب KernelCenterer مصفوفة غرام المركزة المُرتبطة بنواة شبه موجبة \(K\).
الصيغة الرياضية#
يمكننا إلقاء نظرة على الصيغة الرياضية الآن بعد أن أصبح لدينا الحدس. دع \(K\) تكون مصفوفة نواة ذات شكل (n_samples, n_samples) محسوبة من \(X\)، مصفوفة بيانات ذات شكل (n_samples, n_features)، أثناء خطوة fit. يتم تعريف \(K\) بواسطة
\(\phi(X)\) هي دالة تعيين لـ \(X\) إلى فضاء هيلبرت. يتم تعريف نواة مركزة \(\tilde{K}\) على النحو التالي:
حيث تنتج \(\tilde{\phi}(X)\) عن تركيز \(\phi(X)\) في فضاء هيلبرت.
وبالتالي، يمكن للمرء حساب \(\tilde{K}\) عن طريق تعيين \(X\) باستخدام الدالة \(\phi(\cdot)\) وتركيز البيانات في هذه المساحة الجديدة. ومع ذلك، غالبًا ما تُستخدم النوى لأنها تسمح ببعض حسابات الجبر التي تتجنب حساب هذا التعيين بشكل صريح باستخدام \(\phi(\cdot)\). في الواقع، يمكن للمرء أن يركز ضمنيًا كما هو موضح في الملحق B في [Scholkopf1998]:
\(1_{\text{n}_{samples}}\) هي مصفوفة من (n_samples, n_samples) حيث جميع الإدخالات تساوي \(\frac{1}{\text{n}_{samples}}\). في خطوة transform، تُصبح النواة \(K_{test}(X, Y)\) مُعرّفة على النحو التالي:
\(Y\) هي مجموعة بيانات الاختبار ذات الشكل (n_samples_test, n_features)، وبالتالي فإن \(K_{test}\) ذات شكل (n_samples_test, n_samples). في هذه الحالة، يتم تركيز \(K_{test}\) على النحو التالي:
\(1'_{\text{n}_{samples}}\) هي مصفوفة ذات شكل (n_samples_test, n_samples) حيث جميع الإدخالات تساوي \(\frac{1}{\text{n}_{samples}}\).
المراجع
B. Schölkopf, A. Smola, and K.R. Müller, "Nonlinear component analysis as a kernel eigenvalue problem." Neural computation 10.5 (1998): 1299-1319.
6.3.2. التحويل غير الخطي#
يتوفر نوعان من التحويلات: تحويلات الكميات وتحويلات القوة. تعتمد كل من تحويلات الكميات وتحويلات القوة على تحويلات رتيبة للميزات، وبالتالي تحافظ على رتبة القيم على طول كل ميزة.
تضع تحويلات الكميات جميع الميزات في نفس التوزيع المطلوب بناءً على الصيغة \(G^{-1}(F(X))\) حيث \(F\) هي دالة التوزيع التراكمي للميزة و \(G^{-1}\) هي دالة الكمية لتوزيع الإخراج المطلوب \(G\). تستخدم هذه الصيغة الحقيقتين التاليتين: (1) إذا كان \(X\) متغيرًا عشوائيًا مع دالة توزيع تراكمي مُستمرة \(F\)، فإن \(F(X)\) يتم توزيعها بشكل منتظم على \([0,1]\)؛ (2) إذا كان \(U\) متغيرًا عشوائيًا مع توزيع منتظم على \([0,1]\)، فإن \(G^{-1}(U)\) له توزيع \(G\). من خلال إجراء تحويل رتبة، يقوم تحويل الكمية بتنعيم التوزيعات غير العادية ويتأثر بالقيم المتطرفة أقل من أساليب التحجيم(قياس). ومع ذلك، فإنه يُشوّه الارتباطات والمسافات داخل الميزات وعبرها.
تحويلات القوة هي عائلة من التحويلات البارامترية التي تهدف إلى تعيين البيانات من أي توزيع إلى أقرب ما يمكن من التوزيع الغاوسي.
6.3.2.1. التعيين إلى توزيع منتظم#
QuantileTransformer يُوفر تحويلاً غير بارامتري لتعيين البيانات إلى توزيع منتظم بقيم بين 0 و 1:
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
>>> quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
>>> X_train_trans = quantile_transformer.fit_transform(X_train)
>>> X_test_trans = quantile_transformer.transform(X_test)
>>> np.percentile(X_train[:, 0], [0, 25, 50, 75, 100])
array([ 4.3, 5.1, 5.8, 6.5, 7.9])
تتوافق هذه الميزة مع طول الكأس بالسنتيمتر. بمجرد تطبيق تحويل الكمية، تقترب هذه المعالم بشكل وثيق من النسب المئوية المُحدّدة مسبقًا:
>>> np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100])
...
array([ 0.00... , 0.24..., 0.49..., 0.73..., 0.99... ])
يمكن تأكيد ذلك على مجموعة اختبار مستقلة بملاحظات مُماثلة:
>>> np.percentile(X_test[:, 0], [0, 25, 50, 75, 100])
...
array([ 4.4 , 5.125, 5.75 , 6.175, 7.3 ])
>>> np.percentile(X_test_trans[:, 0], [0, 25, 50, 75, 100])
...
array([ 0.01..., 0.25..., 0.46..., 0.60... , 0.94...])
6.3.2.2. التعيين إلى توزيع غاوسي#
في العديد من سيناريوهات النمذجة، يكون التوزيع الطبيعي للميزات في مجموعة بيانات أمرًا مرغوبًا فيه. تحويلات القوة هي عائلة من التحويلات البارامترية والرتيبة التي تهدف إلى تعيين البيانات من أي توزيع إلى أقرب ما يمكن من التوزيع الغاوسي من أجل تثبيت التباين وتقليل الانحراف.
تُوفر PowerTransformer حاليًا تحويلين للقوة، تحويل Yeo-Johnson وتحويل Box-Cox.
تحويل Yeo-Johnson#
تحويل Box-Cox#
لا يمكن تطبيق Box-Cox إلا على البيانات الموجبة تمامًا. في كلتا الطريقتين، يتم تحديد معلمات التحويل بواسطة \(\lambda\)، والتي يتم تحديدها من خلال تقدير أقصى احتمالية. فيما يلي مثال على استخدام Box-Cox لتعيين عينات مأخوذة من توزيع لوغاريتمي عادي إلى توزيع عادي:
>>> pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
>>> X_lognormal = np.random.RandomState(616).lognormal(size=(3, 3))
>>> X_lognormal
array([[1.28..., 1.18..., 0.84...],
[0.94..., 1.60..., 0.38...],
[1.35..., 0.21..., 1.09...]])
>>> pt.fit_transform(X_lognormal)
array([[ 0.49..., 0.17..., -0.15...],
[-0.05..., 0.58..., -0.57...],
[ 0.69..., -0.84..., 0.10...]])
بينما يُعيّن المثال أعلاه خيار standardize إلى False، سيطبق PowerTransformer تطبيع متوسط صفر، تباين وحدة على الإخراج المُحوّل افتراضيًا.
أدناه أمثلة على Box-Cox و Yeo-Johnson مطبقة على توزيعات احتمالية مُختلفة. لاحظ أنه عند تطبيقها على توزيعات مُعينة، تُحقق تحويلات القوة نتائج تُشبه التوزيع الغاوسي، ولكن مع توزيعات أخرى، تكون غير فعالة. يُبرز هذا أهمية تصور البيانات قبل التحويل وبعده.
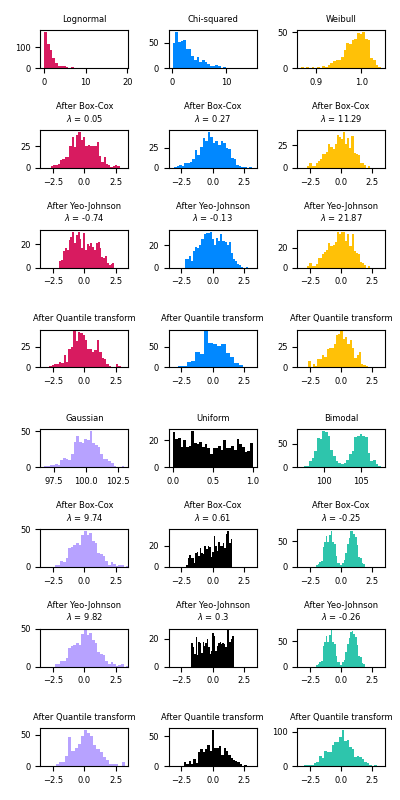
من الممكن أيضًا تعيين البيانات إلى توزيع عادي باستخدام QuantileTransformer عن طريق تعيين output_distribution='normal'. باستخدام المثال السابق مع مجموعة بيانات زهرة القزحية:
>>> quantile_transformer = preprocessing.QuantileTransformer(
... output_distribution='normal', random_state=0)
>>> X_trans = quantile_transformer.fit_transform(X)
>>> quantile_transformer.quantiles_
array([[4.3, 2. , 1. , 0.1],
[4.4, 2.2, 1.1, 0.1],
[4.4, 2.2, 1.2, 0.1],
...,
[7.7, 4.1, 6.7, 2.5],
[7.7, 4.2, 6.7, 2.5],
[7.9, 4.4, 6.9, 2.5]])
وبالتالي، يُصبح وسيط الإدخال هو متوسط الإخراج، مركّزًا عند 0. يتم قص الإخراج العادي بحيث لا يُصبح الحد الأدنى والحد الأقصى للإدخال - المقابلة للكميات 1e-7 و 1 - 1e-7 على التوالي - لانهائية في ظل التحويل.
6.3.3. التطبيع#
التطبيع هو عملية تحجيم(قياس) العينات الفردية للحصول على معيار وحدة. يمكن أن تكون هذه العملية مفيدة إذا كنت تُخطط لاستخدام شكل تربيعي مثل حاصل الضرب النقطي أو أي نواة أخرى لتحديد تشابه أي زوج من العينات.
هذا الافتراض هو أساس نموذج فضاء المتجه الذي غالبًا ما يُستخدم في سياقات تصنيف النصوص وتجميعها.
تُوفر الدالة normalize طريقة سريعة وسهلة لإجراء هذه العملية على مجموعة بيانات واحدة تُشبه المصفوفة، إما باستخدام معايير l1 أو l2 أو max:
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> X_normalized = preprocessing.normalize(X, norm='l2')
>>> X_normalized
array([[ 0.40..., -0.40..., 0.81...],
[ 1. ..., 0. ..., 0. ...],
[ 0. ..., 0.70..., -0.70...]])
تُوفر وحدة preprocessing أيضًا فئة أداة مساعدة Normalizer تُطبق نفس العملية باستخدام واجهة برمجة تطبيقات Transformer (على الرغم من أن طريقة fit غير مجدية في هذه الحالة: الفئة عديمة الحالة لأن هذه العملية تُعالج العينات بشكل مستقل).
وبالتالي، فإن هذه الفئة مُناسبة للاستخدام في الخطوات الأولى من Pipeline:
>>> normalizer = preprocessing.Normalizer().fit(X) # fit لا تفعل شيئًا
>>> normalizer
Normalizer()
يمكن بعد ذلك استخدام مثيل أداة التطبيع على متجهات العينة كأي محول:
>>> normalizer.transform(X)
array([[ 0.40..., -0.40..., 0.81...],
[ 1. ..., 0. ..., 0. ...],
[ 0. ..., 0.70..., -0.70...]])
>>> normalizer.transform([[-1., 1., 0.]])
array([[-0.70..., 0.70..., 0. ...]])
ملاحظة: يُعرف تطبيع L2 أيضًا باسم المعالجة المُسبقة للإشارات المكانية.
مُدخل متفرق#
يقبل كل من normalize و Normalizer كل من البيانات التي تُشبه المصفوفة الكثيفة والمصفوفات المتفرقة من scipy.sparse كمدخلات.
بالنسبة للمُدخل المتفرق، يتم تحويل البيانات إلى تمثيل صفوف متفرقة مضغوطة (انظر scipy.sparse.csr_matrix) قبل تغذيتها إلى إجراءات Cython الفعالة. لتجنب نسخ الذاكرة غير الضرورية، يُوصى باختيار تمثيل CSR في المراحل السابقة.
6.3.4. تشفير الميزات الفئوية#
غالبًا لا تُعطى الميزات كقيم مُستمرة ولكنها فئوية. على سبيل المثال، يمكن أن يكون للشخص ميزات ["ذكر"، "أنثى"]، ["من أوروبا"، "من الولايات المتحدة"، "من آسيا"]، ["يستخدم Firefox"، "يستخدم Chrome"، "يستخدم Safari"، "يستخدم Internet Explorer"]. يمكن تشفير هذه الميزات بكفاءة كأعداد صحيحة، على سبيل المثال، يمكن التعبير عن ["ذكر"، "من الولايات المتحدة"، "يستخدم Internet Explorer"] كـ [0, 1, 3] بينما ["أنثى"، "من آسيا"، "يستخدم Chrome"] ستكون [1, 2, 1].
لتحويل الميزات الفئوية إلى رموز أعداد صحيحة، يمكننا استخدام OrdinalEncoder. يُحوّل هذا المقدّر كل ميزة فئوية إلى ميزة جديدة واحدة من الأعداد الصحيحة (0 إلى n_categories - 1):
>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OrdinalEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari']])
array([[0., 1., 1.]])
مع ذلك، لا يمكن استخدام تمثيل الأعداد الصحيحة هذا مُباشرةً مع جميع مقدرات scikit-learn، حيث تتوقع هذه المقدرات مُدخلات مُستمرة، وستُفسر الفئات على أنها مُرتبة، وهو أمر غير مرغوب فيه غالبًا (أي تم ترتيب مجموعة المُتصفحات بشكل تعسفي).
افتراضيًا، سيقوم OrdinalEncoder أيضًا بتمرير القيم المفقودة التي يُشار إليها بواسطة np.nan.
>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male'], ['female'], [np.nan], ['female']]
>>> enc.fit_transform(X)
array([[ 1.],
[ 0.],
[nan],
[ 0.]])
يُوفر OrdinalEncoder معلمة encoded_missing_value لتشفير القيم المفقودة دون الحاجة إلى إنشاء خط أنابيب واستخدام SimpleImputer.
>>> enc = preprocessing.OrdinalEncoder(encoded_missing_value=-1)
>>> X = [['male'], ['female'], [np.nan], ['female']]
>>> enc.fit_transform(X)
array([[ 1.],
[ 0.],
[-1.],
[ 0.]])
المعالجة أعلاه تُكافئ خط الأنابيب التالي:
>>> from sklearn.pipeline import Pipeline
>>> from sklearn.impute import SimpleImputer
>>> enc = Pipeline(steps=[
... ("encoder", preprocessing.OrdinalEncoder()),
... ("imputer", SimpleImputer(strategy="constant", fill_value=-1)),
... ])
>>> enc.fit_transform(X)
array([[ 1.],
[ 0.],
[-1.],
[ 0.]])
هناك إمكانية أخرى لتحويل الميزات الفئوية إلى ميزات يمكن استخدامها مع مقدرات scikit-learn وهي استخدام واحد من K، والمعروف أيضًا باسم التشفير الأحادي أو التشفير الوهمي. يمكن الحصول على هذا النوع من التشفير باستخدام OneHotEncoder، الذي يُحوّل كل ميزة فئوية ذات n_categories قيم مُمكنة إلى n_categories ميزات ثنائية، إحداها 1، وجميع الميزات الأخرى 0.
استمرارًا للمثال أعلاه:
>>> enc = preprocessing.OneHotEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari'],
... ['male', 'from Europe', 'uses Safari']]).toarray()
array([[1., 0., 0., 1., 0., 1.],
[0., 1., 1., 0., 0., 1.]])
افتراضيًا، يتم استنتاج القيم التي يمكن أن تأخذها كل ميزة تلقائيًا من مجموعة البيانات ويمكن العثور عليها في السمة categories_:
>>> enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]
من الممكن تحديد ذلك صراحةً باستخدام المعلمة categories. هناك جنسان وأربع قارات مُمكنة وأربعة مُتصفحات ويب في مجموعة البيانات لدينا:
>>> genders = ['female', 'male']
>>> locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
>>> browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
>>> enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
>>> # لاحظ أن هناك قيم فئوية مفقودة للميزتين الثانية والثالثة
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(categories=[['female', 'male'],
['from Africa', 'from Asia', 'from Europe',
'from US'],
['uses Chrome', 'uses Firefox', 'uses IE',
'uses Safari']])
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])
إذا كان هناك احتمال أن تحتوي بيانات التدريب على ميزات فئوية مفقودة، فغالبًا ما يكون من الأفضل تحديد handle_unknown='infrequent_if_exist' بدلاً من تعيين categories يدويًا كما هو مذكور أعلاه. عند تحديد handle_unknown='infrequent_if_exist' ومواجهة فئات غير معروفة أثناء التحويل، لن يتم طرح أي خطأ ولكن الأعمدة المُشفّرة أحادية الاتجاه الناتجة لهذه الميزة ستكون جميعها أصفارًا أو تُعتبر فئة نادرة إذا تم تمكينها. (لا يتم دعم handle_unknown='infrequent_if_exist' إلا للتشفير الأحادي):
>>> enc = preprocessing.OneHotEncoder(handle_unknown='infrequent_if_exist')
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(handle_unknown='infrequent_if_exist')
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 0., 0., 0.]])
من الممكن أيضًا تشفير كل عمود في n_categories - 1 أعمدة بدلاً من n_categories أعمدة باستخدام المعلمة drop. تسمح هذه المعلمة للمستخدم بتحديد فئة لكل ميزة يجب إفلاتها. هذا مفيد لتجنب التداخل الخطي في مصفوفة الإدخال في بعض المُصنفات. هذه الوظيفة مفيدة، على سبيل المثال، عند استخدام الانحدار غير المُنظّم (LinearRegression), لأن التداخل الخطي سيؤدي إلى أن تكون مصفوفة التغاير غير قابلة للعكس:
>>> X = [['male', 'from US', 'uses Safari'],
... ['female', 'from Europe', 'uses Firefox']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='first').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object),
array(['uses Firefox', 'uses Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 1., 1.],
[0., 0., 0.]])
قد يرغب المرء في إسقاط أحد العمودين فقط للميزات ذات فئتين. في هذه الحالة، يمكنك تعيين المعلمة drop='if_binary'.
>>> X = [['male', 'US', 'Safari'],
... ['female', 'Europe', 'Firefox'],
... ['female', 'Asia', 'Chrome']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['Asia', 'Europe', 'US'], dtype=object),
array(['Chrome', 'Firefox', 'Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 0., 0., 1., 0., 0., 1.],
[0., 0., 1., 0., 0., 1., 0.],
[0., 1., 0., 0., 1., 0., 0.]])
في X المُحوّلة، العمود الأول هو تشفير الميزة ذات الفئات "ذكر"/"أنثى"، بينما الأعمدة الستة المتبقية هي تشفير الميزتين مع 3 فئات لكل منهما على التوالي.
عندما تكون handle_unknown='ignore' و drop ليست بلا، سيتم تشفير الفئات غير المعروفة على أنها جميعها أصفار:
>>> drop_enc = preprocessing.OneHotEncoder(drop='first',
... handle_unknown='ignore').fit(X)
>>> X_test = [['unknown', 'America', 'IE']]
>>> drop_enc.transform(X_test).toarray()
array([[0., 0., 0., 0., 0.]])
جميع الفئات في X_test غير معروفة أثناء التحويل وسيتم تعيينها إلى جميع الأصفار. هذا يعني أن الفئات غير المعروفة سيكون لها نفس تعيين الفئة المُسقطة. سيقوم OneHotEncoder.inverse_transform بتعيين جميع الأصفار إلى الفئة المُسقطة إذا تم إسقاط فئة و None إذا لم يتم إسقاط فئة:
>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary', sparse_output=False,
... handle_unknown='ignore').fit(X)
>>> X_test = [['unknown', 'America', 'IE']]
>>> X_trans = drop_enc.transform(X_test)
>>> X_trans
array([[0., 0., 0., 0., 0., 0., 0.]])
>>> drop_enc.inverse_transform(X_trans)
array([['female', None, None]], dtype=object)
دعم الميزات الفئوية ذات القيم المفقودة#
يدعم OneHotEncoder الميزات الفئوية ذات القيم المفقودة من خلال اعتبار القيم المفقودة فئة إضافية:
>>> X = [['male', 'Safari'],
... ['female', None],
... [np.nan, 'Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['female', 'male', nan], dtype=object),
array(['Firefox', 'Safari', None], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0., 1., 0.],
[1., 0., 0., 0., 0., 1.],
[0., 0., 1., 1., 0., 0.]])
إذا كانت الميزة تحتوي على كل من np.nan و None، فسيتم اعتبارهما فئتين مُنفصلتين:
>>> X = [['Safari'], [None], [np.nan], ['Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['Firefox', 'Safari', None, nan], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[1., 0., 0., 0.]])
انظر تحميل الميزات من القواميس للميزات الفئوية التي يتم تمثيلها كقاموس، وليس كقيم عددية.
6.3.4.1. الفئات غير المتكررة#
يدعم OneHotEncoder و OrdinalEncoder تجميع الفئات غير المتكررة في مُخرج واحد لكل ميزة. المعلمات لتمكين جمع الفئات غير المتكررة هي min_frequency و max_categories.
min_frequencyهو إما عدد صحيح أكبر من أو يساوي 1، أو عدد عشري في الفترة(0.0, 1.0). إذا كانmin_frequencyعددًا صحيحًا، فسيتم اعتبار الفئات ذات العدد الأصغر منmin_frequencyغير متكررة. إذا كانmin_frequencyعددًا عشريًا، فسيتم اعتبار الفئات ذات العدد الأصغر من هذا الكسر من إجمالي عدد العينات غير متكررة. القيمة الافتراضية هي 1، مما يعني أن كل فئة يتم تشفيرها بشكل مُنفصل.max_categoriesهو إماNoneأو أي عدد صحيح أكبر من 1. تُعيّن هذه المعلمة حدًا أعلى لعدد ميزات الإخراج لكل ميزة إدخال. يتضمنmax_categoriesالميزة التي تُجمّع الفئات غير المتكررة.
في المثال التالي مع OrdinalEncoder، تُعتبر الفئات 'dog' و 'snake' غير متكررة:
>>> X = np.array([['dog'] * 5 + ['cat'] * 20 + ['rabbit'] * 10 +
... ['snake'] * 3], dtype=object).T
>>> enc = preprocessing.OrdinalEncoder(min_frequency=6).fit(X)
>>> enc.infrequent_categories_
[array(['dog', 'snake'], dtype=object)]
>>> enc.transform(np.array([['dog'], ['cat'], ['rabbit'], ['snake']]))
array([[2.],
[0.],
[1.],
[2.]])
max_categories لـ OrdinalEncoder لا تأخذ في الاعتبار الفئات المفقودة أو غير المعروفة. سيؤدي تعيين unknown_value أو encoded_missing_value إلى عدد صحيح إلى زيادة عدد رموز الأعداد الصحيحة الفريدة بمقدار واحد لكل منهما. يمكن أن يؤدي هذا إلى ما يصل إلى max_categories + 2 رموز أعداد صحيحة. في المثال التالي، يتم اعتبار "a" و "d" غير متكررين ويتم تجميعهما معًا في فئة واحدة، و "b" و "c" هما فئتيهما الخاصة، ويتم تشفير القيم غير المعروفة على أنها 3، ويتم تشفير القيم المفقودة على أنها 4.
>>> X_train = np.array(
... [["a"] * 5 + ["b"] * 20 + ["c"] * 10 + ["d"] * 3 + [np.nan]],
... dtype=object).T
>>> enc = preprocessing.OrdinalEncoder(
... handle_unknown="use_encoded_value", unknown_value=3,
... max_categories=3, encoded_missing_value=4)
>>> _ = enc.fit(X_train)
>>> X_test = np.array([["a"], ["b"], ["c"], ["d"], ["e"], [np.nan]], dtype=object)
>>> enc.transform(X_test)
array([[2.],
[0.],
[1.],
[2.],
[3.],
[4.]])
بالمثل، يمكن تكوين OneHotEncoder لتجميع الفئات غير المتكررة معًا:
>>> enc = preprocessing.OneHotEncoder(min_frequency=6, sparse_output=False).fit(X)
>>> enc.infrequent_categories_
[array(['dog', 'snake'], dtype=object)]
>>> enc.transform(np.array([['dog'], ['cat'], ['rabbit'], ['snake']]))
array([[0., 0., 1.],
[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
عن طريق تعيين handle_unknown إلى 'infrequent_if_exist'، سيتم اعتبار الفئات غير المعروفة غير متكررة:
>>> enc = preprocessing.OneHotEncoder(
... handle_unknown='infrequent_if_exist', sparse_output=False, min_frequency=6)
>>> enc = enc.fit(X)
>>> enc.transform(np.array([['dragon']]))
array([[0., 0., 1.]])
يستخدم OneHotEncoder.get_feature_names_out 'infrequent' كاسم للميزة غير المتكررة:
>>> enc.get_feature_names_out()
array(['x0_cat', 'x0_rabbit', 'x0_infrequent_sklearn'], dtype=object)
عندما يتم تعيين 'handle_unknown' إلى 'infrequent_if_exist' وتصادف فئة غير معروفة في التحويل:
إذا لم يتم تكوين دعم الفئة غير المتكررة أو لم تكن هناك فئة غير متكررة أثناء التدريب، فستكون الأعمدة المُشفّرة أحادية الاتجاه الناتجة لهذه الميزة كلها أصفارًا. في التحويل العكسي، سيتم الإشارة إلى الفئة غير المعروفة باسم
None.إذا كانت هناك فئة غير متكررة أثناء التدريب، فسيتم اعتبار الفئة غير المعروفة غير متكررة. في التحويل العكسي، سيتم استخدام 'infrequent_sklearn' لتمثيل الفئة غير المتكررة.
يمكن أيضًا تكوين الفئات غير المتكررة باستخدام max_categories. في المثال التالي، نُعيّن max_categories=2 للحد من عدد الميزات في المخرجات. سيؤدي هذا إلى اعتبار جميع الفئات باستثناء فئة 'cat' غير متكررة، مما يؤدي إلى ميزتين، واحدة لـ 'cat' وواحدة للفئات غير المتكررة - وهي جميع الفئات الأخرى:
>>> enc = preprocessing.OneHotEncoder(max_categories=2, sparse_output=False)
>>> enc = enc.fit(X)
>>> enc.transform([['dog'], ['cat'], ['rabbit'], ['snake']])
array([[0., 1.],
[1., 0.],
[0., 1.],
[0., 1.]])
إذا كانت كل من max_categories و min_frequency قيمًا غير افتراضية، فسيتم تحديد الفئات بناءً على min_frequency أولاً ويتم الاحتفاظ بفئات max_categories. في المثال التالي، تعتبر min_frequency=4 snake فقط غير متكررة، لكن max_categories=3 تُجبر dog على أن تكون غير متكررة أيضًا:
>>> enc = preprocessing.OneHotEncoder(min_frequency=4, max_categories=3, sparse_output=False)
>>> enc = enc.fit(X)
>>> enc.transform([['dog'], ['cat'], ['rabbit'], ['snake']])
array([[0., 0., 1.],
[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
إذا كانت هناك فئات غير متكررة بنفس العدد عند حد max_categories، فسيتم أخذ أول max_categories بناءً على ترتيب المعجم. في المثال التالي، "b" و "c" و "d" لها نفس العدد ومع max_categories=2، "b" و "c" غير متكررتين لأنهما لهما ترتيب معجمي أعلى.
>>> X = np.asarray([["a"] * 20 + ["b"] * 10 + ["c"] * 10 + ["d"] * 10], dtype=object).T
>>> enc = preprocessing.OneHotEncoder(max_categories=3).fit(X)
>>> enc.infrequent_categories_
[array(['b', 'c'], dtype=object)]
6.3.4.2. مُشفّر الهدف#
يستخدم TargetEncoder متوسط الهدف بشرط الميزة الفئوية لتشفير الفئات غير المُرتبة، أي الفئات الاسمية [PAR] [MIC]. يكون مخطط التشفير هذا مفيدًا مع الميزات الفئوية ذات العدد الكبير، حيث سيؤدي التشفير الأحادي إلى تضخيم فضاء الميزات مما يجعله أكثر تكلفة للنموذج اللاحق للمعالجة. من الأمثلة الكلاسيكية للفئات ذات العدد الكبير هي تلك القائمة على الموقع مثل الرمز البريدي أو المنطقة.
أهداف التصنيف الثنائي#
بالنسبة لهدف التصنيف الثنائي، يتم إعطاء تشفير الهدف بواسطة:
حيث \(S_i\) هو تشفير الفئة \(i\)، \(n_{iY}\) هو عدد المشاهدات مع \(Y=1\) والفئة \(i\)، \(n_i\) هو عدد المشاهدات مع الفئة \(i\)، \(n_Y\) هو عدد المشاهدات مع \(Y=1\)، \(n\) هو عدد المشاهدات، و \(\lambda_i\) هو مُعامل الانكماش للفئة \(i\). يتم إعطاء مُعامل الانكماش بواسطة:
حيث \(m\) هو مُعامل تنعيم، يتم التحكم فيه بواسطة معلمة smooth في TargetEncoder. ستضع مُعاملات التنعيم الكبيرة وزنًا أكبر على المتوسط العالمي. عندما تكون smooth="auto"، يتم حساب مُعامل التنعيم كتقدير تجريبي لبايز: \(m=\sigma_i^2/\tau^2\)، حيث \(\sigma_i^2\) هو تباين y مع الفئة \(i\) و:math:tau^2 هو التباين العالمي لـ y.
أهداف التصنيف متعدد الفئات#
بالنسبة لأهداف التصنيف متعدد الفئات، تُشبه الصيغة التصنيف الثنائي:
حيث \(S_{ij}\) هو تشفير الفئة \(i\) والفئة \(j\)، \(n_{iY_j}\) هو عدد المشاهدات مع \(Y=j\) والفئة \(i\)، \(n_i\) هو عدد المشاهدات مع الفئة \(i\)، \(n_{Y_j}\) هو عدد المشاهدات مع \(Y=j\)، \(n\) هو عدد المشاهدات، و \(\lambda_i\) هو مُعامل الانكماش للفئة \(i\).
أهداف مُستمرة#
بالنسبة للأهداف المُستمرة، تُشبه الصيغة التصنيف الثنائي:
حيث \(L_i\) هي مجموعة المشاهدات مع الفئة \(i\) و:math:n_i هو عدد المشاهدات مع الفئة \(i\).
يعتمد fit_transform داخليًا على مخطط cross fitting لمنع معلومات الهدف من التسرب إلى تمثيل وقت التدريب، خاصةً للمتغيرات الفئوية ذات العدد الكبير غير المفيدة، والمساعدة في منع النموذج اللاحق من التوافق الزائد مع الارتباطات الزائفة. لاحظ أنه نتيجة لذلك، fit(X, y).transform(X) لا يساوي fit_transform(X, y). في fit_transform، يتم تقسيم بيانات التدريب إلى k طيات (يتم تحديدها بواسطة معلمة cv) ويتم تشفير كل طية باستخدام عمليات التشفير المُتعلّمة باستخدام الطيات k-1 الأخرى. يُظهر الرسم التخطيطي التالي مخطط cross fitting في fit_transform مع cv=5 الافتراضي:
يتعلم fit_transform أيضًا تشفير "بيانات كاملة" باستخدام مجموعة التدريب بأكملها. لا يتم استخدام هذا أبدًا في fit_transform ولكن يتم حفظه في السمة encodings_، للاستخدام عند استدعاء transform. لاحظ أنه لا يتم حفظ عمليات التشفير المُتعلّمة لكل طية أثناء مخطط cross fitting في سمة.
طريقة fit لا تستخدم أي مخططات cross fitting وتتعلم تشفيرًا واحدًا على مجموعة التدريب بأكملها، والذي يُستخدم لتشفير الفئات في transform. هذا التشفير هو نفسه تشفير "البيانات الكاملة" المُتعلّم في fit_transform.
ملاحظة
يعتبر TargetEncoder القيم المفقودة، مثل np.nan أو None، فئة أخرى ويُشفّرها مثل أي فئة أخرى. يتم تشفير الفئات التي لم تتم رؤيتها أثناء fit بمتوسط الهدف، أي target_mean_.
أمثلة
المراجع
6.3.5. التحويل إلى فئات (التقطيع)#
التحويل إلى فئات (التقطيع) (المعروف باسم التكميم أو التجميع) يُوفر طريقة لتقسيم الميزات المُستمرة إلى قيم منفصلة. قد تستفيد مجموعات بيانات مُعينة ذات ميزات مُستمرة من التحويل إلى فئات (التقطيع)، لأن التحويل إلى فئات (التقطيع) يمكن أن يُحوّل مجموعة البيانات من السمات المُستمرة إلى مجموعة ذات سمات اسمية فقط.
يمكن للميزات المُفردة المُشفّرة أحادية الاتجاه أن تجعل النموذج أكثر تعبيرًا، مع الحفاظ على قابلية التفسير. على سبيل المثال، يمكن للمعالجة المُسبقة باستخدام مُفرد أن تُدخل اللاخطية في النماذج الخطية. للحصول على إمكانيات أكثر تقدمًا، خاصةً الإمكانيات السلسة، انظر إنشاء ميزات متعددة الحدود أدناه.
6.3.5.1. تحويل إلى فئات (تقطيع) K-bins#
KBinsDiscretizer يُفرد الميزات إلى k صناديق:
>>> X = np.array([[ -3., 5., 15 ],
... [ 0., 6., 14 ],
... [ 6., 3., 11 ]])
>>> est = preprocessing.KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)
افتراضيًا، يتم تشفير الإخراج أحادي الاتجاه في مصفوفة متفرقة (انظر تشفير الميزات الفئوية) ويمكن تكوين ذلك باستخدام المعلمة encode. لكل ميزة، يتم حساب حواف الصناديق أثناء fit وستُحدّد مع عدد الصناديق الفترات. لذلك، بالنسبة للمثال الحالي، يتم تعريف هذه الفترات على النحو التالي:
الميزة 1: \({[-\infty, -1), [-1, 2), [2, \infty)}\)
الميزة 2: \({[-\infty, 5), [5, \infty)}\)
الميزة 3: \({[-\infty, 14), [14, \infty)}\)
بناءً على فترات الصناديق هذه، يتم تحويل X على النحو التالي:
>>> est.transform(X)
array([[ 0., 1., 1.],
[ 1., 1., 1.],
[ 2., 0., 0.]])
تحتوي مجموعة البيانات الناتجة على سمات ترتيبية يمكن استخدامها بشكل أكبر في Pipeline.
يُشبه التحويل إلى فئات (التقطيع) إنشاء رسوم بيانية للبيانات المُستمرة. ومع ذلك، تُركز الرسوم البيانية على حساب الميزات التي تقع في صناديق مُحدّدة، بينما يُركز التحويل إلى فئات (التقطيع) على تعيين قيم الميزات لهذه الصناديق.
تُطبّق KBinsDiscretizer استراتيجيات تجميع مختلفة، والتي يمكن تحديدها باستخدام المعلمة strategy. تستخدم استراتيجية 'uniform' صناديق ذات عرض ثابت. تستخدم استراتيجية 'quantile' قيم الكميات للحصول على صناديق مأهولة بالتساوي في كل ميزة. تُحدّد استراتيجية 'kmeans' الصناديق بناءً على إجراء تجميع k-means يتم إجراؤه على كل ميزة بشكل مستقل.
انتبه إلى أنه يمكن للمرء تحديد صناديق مخصصة عن طريق تمرير قيمة قابلة للاستدعاء تُحدّد استراتيجية التحويل إلى فئات (التقطيع) إلى FunctionTransformer. على سبيل المثال، يمكننا استخدام دالة Pandas pandas.cut:
>>> import pandas as pd
>>> import numpy as np
>>> from sklearn import preprocessing
>>>
>>> bins = [0, 1, 13, 20, 60, np.inf]
>>> labels = ['infant', 'kid', 'teen', 'adult', 'senior citizen']
>>> transformer = preprocessing.FunctionTransformer(
... pd.cut, kw_args={'bins': bins, 'labels': labels, 'retbins': False}
... )
>>> X = np.array([0.2, 2, 15, 25, 97])
>>> transformer.fit_transform(X)
['infant', 'kid', 'teen', 'adult', 'senior citizen']
Categories (5, object): ['infant' < 'kid' < 'teen' < 'adult' < 'senior citizen']
أمثلة
6.3.5.2. تجزئة الميزات#
تجزئة الميزات هي عملية تحديد عتبة للميزات الرقمية للحصول على قيم منطقية. يمكن أن يكون هذا مفيدًا لمقدرات الاحتمالية اللاحقة التي تفترض أن بيانات الإدخال موزعة وفقًا لـ توزيع برنولي متعدد المتغيرات. على سبيل المثال، هذا هو الحال بالنسبة لـ BernoulliRBM.
من الشائع أيضًا بين مجتمع معالجة النصوص استخدام قيم ميزات ثنائية (ربما لتبسيط التفكير الاحتمالي) حتى لو كانت الأعداد المُطبيعة (المعروفة أيضًا باسم ترددات المصطلحات) أو ميزات TF-IDF ذات القيمة غالبًا ما تُؤدي أداءً أفضل قليلاً في الممارسة العملية.
أما بالنسبة لـ Normalizer، فإن فئة الأداة المساعدة Binarizer مخصصة للاستخدام في المراحل الأولى من Pipeline. لا تفعل طريقة fit شيئًا حيث يتم التعامل مع كل عينة بشكل مستقل عن الآخرين:
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> binarizer = preprocessing.Binarizer().fit(X) # fit لا تفعل شيئًا
>>> binarizer
Binarizer()
>>> binarizer.transform(X)
array([[1., 0., 1.],
[1., 0., 0.],
[0., 1., 0.]])
من الممكن ضبط عتبة أداة التجزئة:
>>> binarizer = preprocessing.Binarizer(threshold=1.1)
>>> binarizer.transform(X)
array([[0., 0., 1.],
[1., 0., 0.],
[0., 0., 0.]])
أما بالنسبة لفئة Normalizer، فإن وحدة المعالجة المُسبقة تُوفر دالة مُصاحبة binarize لاستخدامها عندما لا تكون واجهة برمجة تطبيقات المحول ضرورية.
لاحظ أن Binarizer تُشبه KBinsDiscretizer عندما k = 2، وعندما تكون حافة الصندوق عند القيمة threshold.
6.3.6. إسناد القيم المفقودة#
تمت مناقشة أدوات إسناد القيم المفقودة في تعويض القيم المفقودة.
6.3.7. إنشاء ميزات متعددة الحدود#
غالبًا ما يكون من المفيد إضافة تعقيد إلى نموذج من خلال اعتبار الميزات غير الخطية لبيانات الإدخال. نُظهر إمكانيتين تعتمدان كلاهما على كثيرات الحدود: الأولى تستخدم كثيرات الحدود الصرفة، والثانية تستخدم منحنيات متعددة التعريف، أي كثيرات حدود متعددة التعريف.
6.3.7.1. ميزات متعددة الحدود#
إحدى الطرق البسيطة والشائعة هي ميزات كثيرات الحدود، والتي يمكنها الحصول على مصطلحات تفاعل ورتبة عالية للميزات. يتم تطبيقها في PolynomialFeatures:
>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
[2, 3],
[4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])
تم تحويل ميزات X من \((X_1, X_2)\) إلى \((1, X_1, X_2, X_1^2, X_1X_2, X_2^2)\).
في بعض الحالات، تكون مصطلحات التفاعل بين الميزات مطلوبة فقط، ويمكن الحصول عليها من خلال الإعداد interaction_only=True:
>>> X = np.arange(9).reshape(3, 3)
>>> X
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> poly = PolynomialFeatures(degree=3, interaction_only=True)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 2., 0., 0., 2., 0.],
[ 1., 3., 4., 5., 12., 15., 20., 60.],
[ 1., 6., 7., 8., 42., 48., 56., 336.]])
تم تحويل ميزات X من \((X_1, X_2, X_3)\) إلى \((1, X_1, X_2, X_3, X_1X_2, X_1X_3, X_2X_3, X_1X_2X_3)\).
لاحظ أنه يتم استخدام ميزات كثيرات الحدود ضمنيًا في طرق النواة (على سبيل المثال، SVC، KernelPCA) عند استخدام دوال النواة متعددة الحدود.
انظر التكامل متعدد الحدود والتقسيم لانحدار ريدج باستخدام ميزات متعددة الحدود التي تم إنشاؤها.
6.3.7.2. محول المنحنيات المتعددة التعريف#
هناك طريقة أخرى لإضافة مصطلحات غير خطية بدلاً من كثيرات الحدود الصرفة للميزات وهي إنشاء دوال أساس منحنيات متعددة التعريف لكل ميزة مع SplineTransformer. منحنيات متعددة التعريف هي كثيرات حدود متعددة التعريف، معلماتها هي درجتها كثيرة الحدود ومواقع العقد. يُطبّق SplineTransformer أساس B-spline، راجع المراجع أدناه.
ملاحظة
يعامل SplineTransformer كل ميزة على حدة، أي أنه لن يُعطيك مصطلحات تفاعل.
بعض مزايا منحنيات متعددة التعريف على كثيرات الحدود هي:
منحنيات B-spline مرنة للغاية وقوية إذا حافظت على درجة منخفضة ثابتة، عادةً 3، وقمت بتكييف عدد العقد بشكل مقتصد. ستحتاج كثيرات الحدود إلى درجة أعلى، مما يؤدي إلى النقطة التالية.
لا تُظهر منحنيات B-spline سلوكًا متذبذبًا عند الحدود كما هو الحال مع كثيرات الحدود (كلما ارتفعت الدرجة، زاد الأمر سوءًا). يُعرف هذا باسم ظاهرة رونج.
تُوفر منحنيات B-spline خيارات جيدة للاستقراء خارج الحدود، أي خارج نطاق القيم المُناسبة. ألقِ نظرة على الخيار
extrapolation.تُولّد منحنيات B-spline مصفوفة ميزات ذات بنية مُقيدة. بالنسبة لميزة واحدة، يحتوي كل صف على
degree + 1عناصر غير صفرية فقط، والتي تحدث على التوالي وهي موجبة. ينتج عن هذا مصفوفة ذات خصائص عددية جيدة، على سبيل المثال، رقم حالة منخفض، على عكس مصفوفة كثيرات الحدود، والتي تحمل اسم مصفوفة فانديرموند. رقم الحالة المنخفض مهم للخوارزميات المُستقرة للنماذج الخطية.
يُظهر مقتطف الشفرة التالي منحنيات متعددة التعريف قيد التنفيذ:
>>> import numpy as np
>>> from sklearn.preprocessing import SplineTransformer
>>> X = np.arange(5).reshape(5, 1)
>>> X
array([[0],
[1],
[2],
[3],
[4]])
>>> spline = SplineTransformer(degree=2, n_knots=3)
>>> spline.fit_transform(X)
array([[0.5 , 0.5 , 0. , 0. ],
[0.125, 0.75 , 0.125, 0. ],
[0. , 0.5 , 0.5 , 0. ],
[0. , 0.125, 0.75 , 0.125],
[0. , 0. , 0.5 , 0.5 ]])
نظرًا لفرز X، يمكن للمرء بسهولة رؤية إخراج المصفوفة المُقيدة. الأقطار الثلاثة الوسطى فقط غير صفرية لـ degree=2. كلما ارتفعت الدرجة، زاد تداخل منحنيات متعددة التعريف.
من المثير للاهتمام أن SplineTransformer من degree=0 هي نفس KBinsDiscretizer مع encode='onehot-dense' و n_bins = n_knots - 1 إذا كان knots = strategy.
أمثلة
المراجع#
Eilers, P., & Marx, B. (1996). Flexible Smoothing with B-splines and Penalties. Statist. Sci. 11 (1996), no. 2, 89--121.
Perperoglou, A., Sauerbrei, W., Abrahamowicz, M. et al. A review of spline function procedures in R. BMC Med Res Methodol 19, 46 (2019).
6.3.8. محولات مخصصة#
غالبًا ما تُريد تحويل دالة بايثون موجودة إلى محول للمساعدة في تنظيف البيانات أو معالجتها. يمكنك تطبيق محول من دالة عشوائية باستخدام FunctionTransformer. على سبيل المثال، لبناء محول يطبق تحويلًا لوغاريتميًا في خط أنابيب، قم بما يلي:
>>> import numpy as np
>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p, validate=True)
>>> X = np.array([[0, 1], [2, 3]])
>>> # نظرًا لأن FunctionTransformer لا تعمل أثناء الملاءمة، يمكننا استدعاء التحويل مُباشرةً
>>> transformer.transform(X)
array([[0. , 0.69314718],
[1.09861229, 1.38629436]])
يمكنك التأكد من أن func و inverse_func هما معكوس كل منهما للآخر عن طريق تعيين check_inverse=True واستدعاء fit قبل transform. يرجى ملاحظة أنه يتم طرح تحذير ويمكن تحويله إلى خطأ باستخدام filterwarnings:
>>> import warnings
>>> warnings.filterwarnings("error", message=".*check_inverse*.",
... category=UserWarning, append=False)
للحصول على مثال شفرة كامل يُوضح استخدام FunctionTransformer لاستخراج الميزات من بيانات نصية، انظر محول الأعمدة مع مصادر بيانات غير متجانسة و هندسة الميزات ذات الصلة بالوقت.
