1.4. آلات الدعم المتجهية (SVM)#

آلات الدعم المتجهية (SVM) (SVMs) هي مجموعة من أساليب التعلم الخاضعة للإشراف تُستخدم لـ التصنيف و الانحدار و كشف القيم المتطرفة.

مزايا آلات الدعم المتجهية (SVM) هي:

  • فعالة في المساحات عالية الأبعاد.

  • لا تزال فعالة في الحالات التي يكون فيها عدد الأبعاد أكبر من عدد العينات.

  • تستخدم مجموعة فرعية من نقاط التدريب في دالة القرار (تُسمى متجهات الدعم)، لذا فهي فعالة أيضًا في الذاكرة.

  • مُتعدّدة الاستخدامات: يمكن تحديد دوال النواة مختلفة لدالة القرار. يتم توفير النوى الشائعة، ولكن من الممكن أيضًا تحديد نوى مخصصة.

تشمل عيوب آلات الدعم المتجهية (SVM) ما يلي:

  • إذا كان عدد الميزات أكبر بكثير من عدد العينات، فتجنب التوافق الزائد في اختيار دوال النواة ومصطلح التنظيم أمر بالغ الأهمية.

  • لا تُوفر SVMs تقديرات احتمالية مُباشرةً، ويتم حسابها باستخدام تحقق متبادل خماسي مُكلف (انظر الدرجات والاحتمالات، أدناه).

تدعم آلات الدعم المتجهية (SVM) في scikit-learn كلاً من متجهات العينة الكثيفة (numpy.ndarray والقابلة للتحويل إلى ذلك بواسطة numpy.asarray) والمتفرقة (أي scipy.sparse) كمدخلات. ومع ذلك، لاستخدام SVM لإجراء تنبؤات للبيانات المتفرقة، يجب أن تكون مُناسبة لمثل هذه البيانات. للحصول على أداء مثالي، استخدم numpy.ndarray (كثيفة) مُرتبة حسب C أو scipy.sparse.csr_matrix (متفرقة) مع dtype=float64.

1.4.1. التصنيف#

SVC و NuSVC و LinearSVC هي فئات قادرة على إجراء تصنيف ثنائي ومتعدد الفئات على مجموعة بيانات.

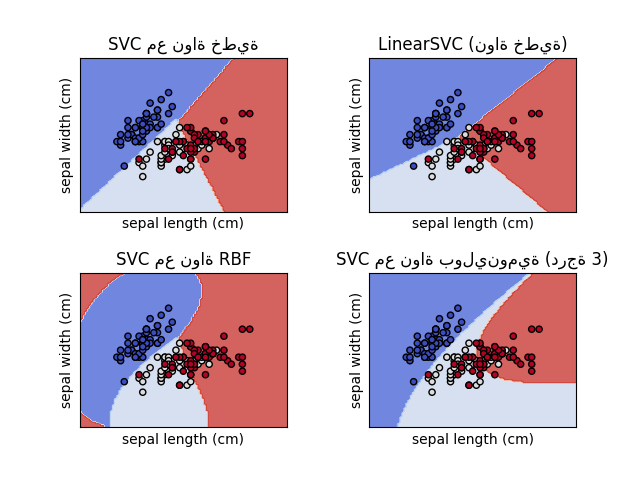
../_images/sphx_glr_plot_iris_svc_001.png

SVC و NuSVC طريقتان مُتشابهتان، لكنهما تقبلان مجموعات مختلفة قليلاً من المعلمات ولها صيغ رياضية مختلفة (انظر القسم الصيغة الرياضية). من ناحية أخرى، LinearSVC هو تطبيق آخر (أسرع) لتصنيف متجه الدعم في حالة النواة الخطية. كما أنه يفتقر إلى بعض سمات SVC و NuSVC، مثل support_. يستخدم LinearSVC خسارة squared_hinge، وبسبب تطبيقه في liblinear، فإنه يُنظّم أيضًا التقاطع، إذا تم اعتباره. ومع ذلك، يمكن تقليل هذا التأثير عن طريق الضبط الدقيق لمعلمة intercept_scaling، والتي تسمح لمصطلح التقاطع بأن يكون له سلوك تنظيم مختلف مقارنة بالميزات الأخرى. لذلك، يمكن أن تختلف نتائج التصنيف والدرجة عن المُصنفين الآخرين.

كمُصنفات أخرى، يأخذ SVC و NuSVC و LinearSVC مصفوفتين كمدخلات: مصفوفة X ذات شكل (n_samples, n_features) تحتوي على عينات التدريب، ومصفوفة y من تسميات الفئات (سلاسل أو أعداد صحيحة)، ذات شكل (n_samples):

>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC()
>>> clf.fit(X, y)
SVC()

بعد الملاءمة، يمكن استخدام النموذج للتنبؤ بقيم جديدة:

>>> clf.predict([[2., 2.]])
array([1])

تعتمد دالة قرار SVMs (مُفصلة في الصيغة الرياضية) على مجموعة فرعية من بيانات التدريب، تُسمى متجهات الدعم. يمكن العثور على بعض خصائص متجهات الدعم هذه في السمات support_vectors_ و support_ و n_support_:

>>> # الحصول على متجهات الدعم
>>> clf.support_vectors_
array([[0., 0.],
       [1., 1.]])
>>> # الحصول على مؤشرات متجهات الدعم
>>> clf.support_
array([0, 1]...)
>>> # الحصول على عدد متجهات الدعم لكل فئة
>>> clf.n_support_
array([1, 1]...)

أمثلة

1.4.1.1. تصنيف متعدد الفئات#

يُطبّق SVC و NuSVC نهج "واحد مقابل واحد" لتصنيف متعدد الفئات. في المجموع، يتم إنشاء n_classes * (n_classes - 1) / 2 مُصنّفًا ويُدرّب كل منها بيانات من فئتين. لتوفير واجهة متسقة مع المُصنفات الأخرى، يسمح خيار decision_function_shape بالتحويل الرتيب لنتائج مُصنفات "واحد مقابل واحد" إلى دالة قرار "واحد مقابل البقية" ذات شكل (n_samples, n_classes)، وهو الإعداد الافتراضي للمعلمة (default='ovr').

>>> X = [[0], [1], [2], [3]]
>>> Y = [0, 1, 2, 3]
>>> clf = svm.SVC(decision_function_shape='ovo')
>>> clf.fit(X, Y)
SVC(decision_function_shape='ovo')
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 6 فئات: 4*3/2 = 6
6
>>> clf.decision_function_shape = "ovr"
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 فئات
4

من ناحية أخرى، يُطبّق LinearSVC إستراتيجية "واحد مقابل البقية" متعددة الفئات، وبالتالي يُدرّب n_classes نماذج.

>>> lin_clf = svm.LinearSVC()
>>> lin_clf.fit(X, Y)
LinearSVC()
>>> dec = lin_clf.decision_function([[1]])
>>> dec.shape[1]
4

انظر الصيغة الرياضية للحصول على وصف كامل لدالة القرار.

تفاصيل حول استراتيجيات متعددة الفئات#

لاحظ أن LinearSVC يُطبّق أيضًا إستراتيجية بديلة متعددة الفئات، ما يُسمى بـ SVM متعدد الفئات الذي وضعه كرامر وسينغر [16]، باستخدام الخيار multi_class='crammer_singer'. في الممارسة العملية، يُفضّل عادةً التصنيف واحد مقابل البقية، حيث أن النتائج متشابهة في الغالب، لكن وقت التشغيل أقل بكثير.

بالنسبة لـ LinearSVC "واحد مقابل البقية"، فإن السمتين coef_ و intercept_ لهما شكل (n_classes, n_features) و (n_classes,) على التوالي. يتوافق كل صف من المعاملات مع واحد من مُصنفات n_classes "واحد مقابل البقية" ومثل ذلك بالنسبة للقطوع، بترتيب فئة "الواحد".

في حالة SVC "واحد مقابل واحد" و NuSVC، يكون تخطيط السمات أكثر تعقيدًا بعض الشيء. في حالة النواة الخطية، يكون للسمتين coef_ و intercept_ شكل (n_classes * (n_classes - 1) / 2, n_features) و (n_classes * (n_classes - 1) / 2) على التوالي. هذا مشابه لتخطيط LinearSVC الموضح أعلاه، حيث يتوافق كل صف الآن مع مُصنف ثنائي. الترتيب للفئات من 0 إلى n هو "0 مقابل 1"، "0 مقابل 2"، ... "0 مقابل n"، "1 مقابل 2"، "1 مقابل 3"، "1 مقابل n"،. . . "n-1 مقابل n".

شكل dual_coef_ هو (n_classes-1, n_SV) بتخطيط يصعب فهمه إلى حد ما. تتوافق الأعمدة مع متجهات الدعم المُشاركة في أي من مُصنفات n_classes * (n_classes - 1) / 2 "واحد مقابل واحد". يحتوي كل متجه دعم v على معامل مُزدوج في كل من مُصنفات n_classes - 1 التي تُقارن فئة v بفئة أخرى. لاحظ أن بعض هذه المعاملات المزدوجة، وليس كلها، قد تكون صفرًا. إدخالات n_classes - 1 في كل عمود هي هذه المعاملات المزدوجة، مُرتبة حسب الفئة المُقابلة.

قد يكون هذا أكثر وضوحًا بمثال: ضع في اعتبارك مشكلة ثلاث فئات حيث تحتوي الفئة 0 على ثلاثة متجهات دعم \(v^{0}_0, v^{1}_0, v^{2}_0\) والفئة 1 و 2 تحتوي على متجهي دعم \(v^{0}_1, v^{1}_1\) و \(v^{0}_2, v^{1}_2\) على التوالي. لكل متجه دعم \(v^{j}_i\)، هناك معاملان مُزدوجان. دعنا نُسمي مُعامل متجه الدعم \(v^{j}_i\) في المُصنف بين الفئات \(i\) و \(k\) \(\alpha^{j}_{i,k}\). ثم dual_coef_ تبدو كالتالي:

أمثلة

1.4.1.2. الدرجات والاحتمالات#

تُعطي طريقة decision_function لـ SVC و NuSVC درجات لكل فئة لكل عينة (أو درجة واحدة لكل عينة في الحالة الثنائية). عندما يتم تعيين خيار المُنشئ probability إلى True، يتم تمكين تقديرات احتمال عضوية الفئة (من الطريقتين predict_proba و predict_log_proba). في الحالة الثنائية، تتم معايرة الاحتمالات باستخدام قياس بلات [9]: الانحدار اللوجستي على درجات SVM، مُناسب بواسطة تحقق متبادل إضافي على بيانات التدريب. في حالة متعددة الفئات، يتم تمديد هذا وفقًا لـ [10].

ملاحظة

إجراء معايرة الاحتمال نفسه مُتاح لجميع المقدرات عبر CalibratedClassifierCV (انظر معايرة الاحتمال). في حالة SVC و NuSVC، يكون هذا الإجراء مُدمجًا في libsvm الذي يُستخدم تحت الغطاء، لذا فهو لا يعتمد على CalibratedClassifierCV لـ scikit-learn.

التحقق المتبادل المُشارك في قياس بلات هو عملية مُكلفة لمجموعات البيانات الكبيرة. بالإضافة إلى ذلك، قد لا تتوافق تقديرات الاحتمالية مع الدرجات:

  • قد لا يكون "argmax" للدرجات هو argmax للاحتمالات

  • في التصنيف الثنائي، قد يتم تسمية عينة بواسطة predict على أنها تنتمي إلى الفئة الإيجابية حتى إذا كان ناتج predict_proba أقل من 0.5؛ وبالمثل، يمكن تسميتها سلبية حتى لو كان ناتج predict_proba أكبر من 0.5.

من المعروف أيضًا أن طريقة بلات بها مشاكل نظرية. إذا كانت درجات الثقة مطلوبة، لكن لا يجب أن تكون احتمالات، فمن المستحسن تعيين probability=False واستخدام decision_function بدلاً من predict_proba.

يرجى ملاحظة أنه عندما decision_function_shape='ovr' و n_classes > 2، على عكس decision_function، لا تحاول طريقة predict كسر الروابط افتراضيًا. يمكنك تعيين break_ties=True ليكون ناتج predict هو نفسه np.argmax(clf.decision_function(...), axis=1)، وإلا فسيتم دائمًا إرجاع الفئة الأولى بين الفئات المُتعادلة؛ لكن ضع في اعتبارك أن ذلك يأتي بتكلفة حسابية. انظر مثال على كسر التعادل في SVM للحصول على مثال لكسر الروابط.

1.4.1.3. المشاكل غير المتوازنة#

في المشاكل التي يكون من المرغوب فيه إعطاء أهمية أكبر لفئات مُعينة أو عينات فردية مُعينة، يمكن استخدام المعلمتين class_weight و sample_weight.

SVC (ولكن ليس NuSVC) تُطبق المعلمة class_weight في طريقة fit. إنه قاموس بالشكل {class_label : value}، حيث القيمة هي رقم فاصلة عائمة > 0 يُعيّن المعلمة C للفئة class_label إلى C * value. يُوضح الشكل أدناه حد القرار لمشكلة غير متوازنة، مع أو بدون تصحيح الوزن.

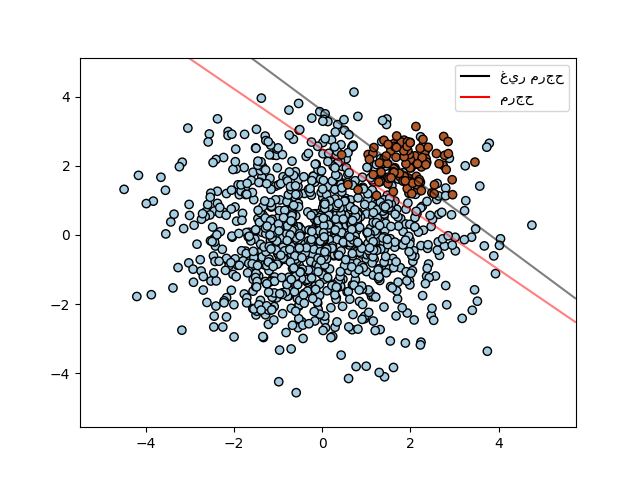
../_images/sphx_glr_plot_separating_hyperplane_unbalanced_001.png

تُطبق SVC و NuSVC و SVR و NuSVR و LinearSVC و LinearSVR و OneClassSVM أيضًا أوزانًا للعينات الفردية في طريقة fit من خلال المعلمة sample_weight. على غرار class_weight، يُعيّن هذا المعلمة C للمثال i إلى C * sample_weight[i]، مما سيُشجع المُصنف على تصحيح هذه العينات. يُوضح الشكل أدناه تأثير ترجيح العينة على حد القرار. حجم الدوائر يتناسب مع أوزان العينة:

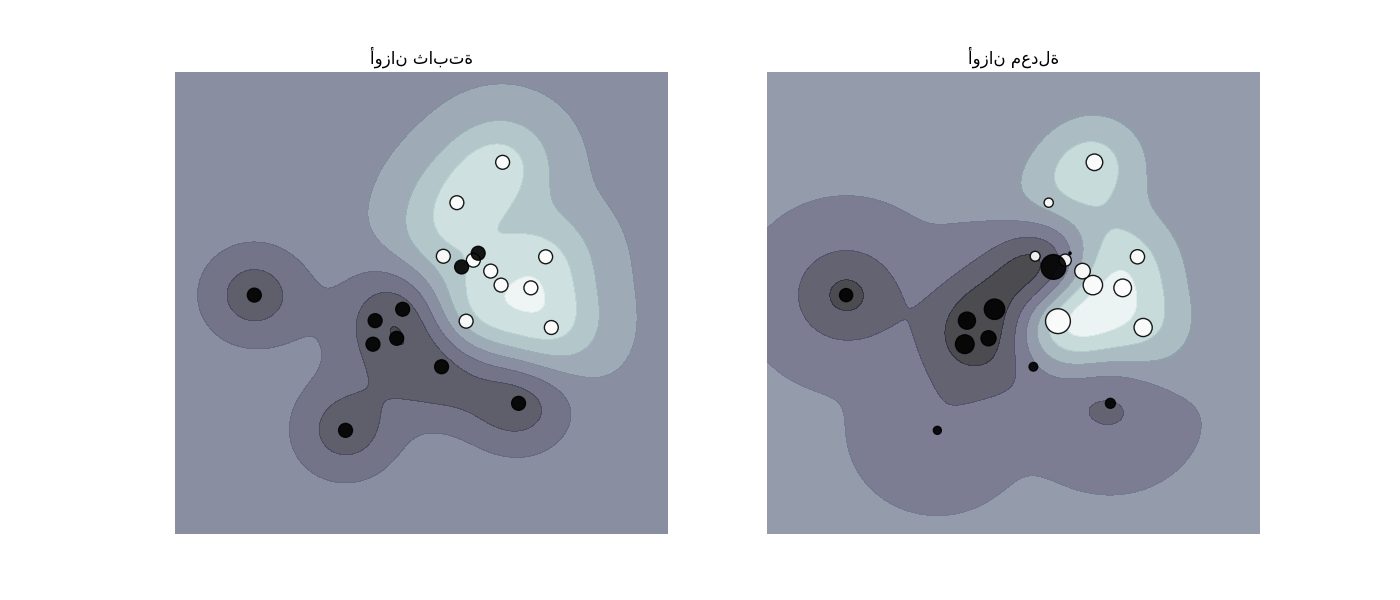
../_images/sphx_glr_plot_weighted_samples_001.png

أمثلة

1.4.2. الانحدار#

يمكن تمديد طريقة تصنيف متجه الدعم لحل مشاكل الانحدار. تُسمى هذه الطريقة انحدار متجه الدعم.

يعتمد النموذج الذي تم إنشاؤه بواسطة تصنيف متجه الدعم (كما هو موضح أعلاه) على مجموعة فرعية فقط من بيانات التدريب، لأن دالة التكلفة لبناء النموذج لا تهتم بنقاط التدريب التي تقع خارج الهامش. وبالمثل، يعتمد النموذج الذي تم إنشاؤه بواسطة انحدار متجه الدعم على مجموعة فرعية فقط من بيانات التدريب، لأن دالة التكلفة تتجاهل العينات التي يكون تنبؤها قريبًا من هدفها.

هناك ثلاثة تطبيقات مختلفة لانحدار متجه الدعم: SVR و NuSVR و LinearSVR. يُوفر LinearSVR تطبيقًا أسرع من SVR ولكنه يأخذ في الاعتبار النواة الخطية فقط، بينما يُطبّق NuSVR صيغة مختلفة قليلاً عن SVR و LinearSVR. نظرًا لتطبيقه في liblinear، فإن LinearSVR يُنظّم أيضًا التقاطع، إذا تم اعتباره. ومع ذلك، يمكن تقليل هذا التأثير عن طريق الضبط الدقيق لمعلمة intercept_scaling، والتي تسمح لمصطلح التقاطع بأن يكون له سلوك تنظيم مختلف مقارنة بالميزات الأخرى. لذلك، يمكن أن تختلف نتائج التصنيف والدرجة عن المُصنفين الآخرين. انظر تفاصيل التطبيق لمزيد من التفاصيل.

كما هو الحال مع فئات التصنيف، ستأخذ طريقة الملاءمة المتجهات X و y كوسيطات، إلا أنه في هذه الحالة، من المتوقع أن يكون لـ y قيم فاصلة عائمة بدلاً من القيم الصحيحة:

>>> from sklearn import svm
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> regr = svm.SVR()
>>> regr.fit(X, y)
SVR()
>>> regr.predict([[1, 1]])
array([1.5])

أمثلة

1.4.3. تقدير الكثافة، كشف الجدة#

تُطبق الفئة OneClassSVM One-Class SVM الذي يُستخدم في كشف القيم المتطرفة.

انظر كشف القيم الغريبة والقيم المتطرفة لوصف واستخدام OneClassSVM.

1.4.4. التعقيد#

تُعد آلات الدعم المتجهية (SVM) أدوات قوية، لكن متطلبات الحساب والتخزين الخاصة بها تزداد بسرعة مع عدد متجهات التدريب. جوهر SVM هو مشكلة برمجة تربيعية (QP)، تفصل متجهات الدعم عن باقي بيانات التدريب. يتدرج مُحلل QP المستخدم بواسطة التطبيق القائم على libsvm بين \(O(n_{features} \times n_{samples}^2)\) و \(O(n_{features} \times n_{samples}^3)\) اعتمادًا على مدى كفاءة استخدام ذاكرة التخزين المؤقت libsvm في الممارسة العملية (يعتمد على مجموعة البيانات). إذا كانت البيانات متفرقة جدًا، فيجب استبدال \(n_{features}\) بمتوسط عدد الميزات غير الصفرية في متجه عينة.

بالنسبة للحالة الخطية، فإن الخوارزمية المستخدمة في LinearSVC بواسطة تطبيق liblinear أكثر كفاءة بكثير من نظيرتها SVC القائمة على libsvm ويمكنها التوسع بشكل خطي تقريبًا إلى ملايين العينات و/أو الميزات.

1.4.5. نصائح حول الاستخدام العملي#

  • تجنب نسخ البيانات: بالنسبة لـ SVC و SVR و NuSVC و NuSVR، إذا كانت البيانات التي تم تمريرها إلى طرق مُعينة غير متجاورة مرتبة حسب C وبدقة مُزدوجة، فسيتم نسخها قبل استدعاء تطبيق C الأساسي. يمكنك التحقق مما إذا كانت مصفوفة numpy مُعطاة متجاورة مرتبة حسب C عن طريق فحص سمة flags.

    بالنسبة لـ LinearSVC (و LogisticRegression)، سيتم نسخ أي مُدخلات تم تمريرها كمصفوفة numpy وتحويلها إلى تمثيل البيانات المتفرقة الداخلي لـ liblinear (أعداد عائمة بدقة مُزدوجة ومؤشرات int32 للمكونات غير الصفرية). إذا كنت تُريد ملاءمة مُصنف خطي واسع النطاق دون نسخ مصفوفة كثيفة مرتبة حسب C بدقة مُزدوجة كمدخلات، فإننا نقترح استخدام فئة SGDClassifier بدلاً من ذلك. يمكن تكوين دالة الهدف لتكون تقريبًا نفس نموذج LinearSVC.

  • حجم ذاكرة التخزين المؤقت للنواة: بالنسبة لـ SVC و SVR و NuSVC و NuSVR، فإن حجم ذاكرة التخزين المؤقت للنواة له تأثير قوي على أوقات التشغيل للمشاكل الأكبر. إذا كان لديك ذاكرة وصول عشوائي (RAM) كافية مُتاحة، فمن المُوصى به تعيين cache_size إلى قيمة أعلى من القيمة الافتراضية 200 (ميغابايت)، مثل 500 (ميغابايت) أو 1000 (ميغابايت).

  • تعيين C: C هي 1 افتراضيًا وهي خيار افتراضي معقول. إذا كان لديك الكثير من المشاهدات المزعجة، فيجب عليك تقليلها: تقليل C يقابل المزيد من التنظيم.

    LinearSVC و LinearSVR أقل حساسية لـ C عندما تُصبح كبيرة، وتتوقف نتائج التنبؤ عن التحسن بعد عتبة مُعينة. في هذه الأثناء، ستستغرق قيم C الأكبر وقتًا أطول للتدريب، وأحيانًا تصل إلى 10 مرات أطول، كما هو موضح في [11].

  • خوارزميات آلة متجه الدعم ليست ثابتة المقياس، لذلك يُوصى بشدة بقياس بياناتك. على سبيل المثال، قم بقياس كل سمة على متجه الإدخال X إلى [0,1] أو [-1,+1]، أو قم بتوحيدها قياسيًا للحصول على متوسط 0 وتباين 1. لاحظ أنه يجب تطبيق نفس القياس على متجه الاختبار للحصول على نتائج ذات مغزى. يمكن القيام بذلك بسهولة باستخدام Pipeline:

    >>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> from sklearn.svm import SVC

>>> clf = make_pipeline(StandardScaler(), SVC())

    انظر القسم المعالجة المسبقة للبيانات لمزيد من التفاصيل حول القياس والتطبيع.

  • فيما يتعلق بمعلمة shrinking، نقلاً عن [12]: وجدنا أنه إذا كان عدد التكرارات كبيرًا، فيمكن للانكماش تقصير وقت التدريب. ومع ذلك، إذا قمنا بحل مشكلة التحسين بشكل فضفاض (على سبيل المثال، باستخدام تفاوت إيقاف كبير)، فقد يكون الرمز بدون استخدام الانكماش أسرع بكثير

  • تُقارب المعلمة nu في NuSVC/OneClassSVM/NuSVR جزء أخطاء متجهات الدعم والهامش.

  • في SVC، إذا كانت البيانات غير متوازنة (على سبيل المثال، الكثير من الإيجابيات وقليل من السلبيات)، فعيّن class_weight='balanced' و/أو جرب معلمات جزاء مختلفة C.

  • عشوائية التطبيقات الأساسية: تستخدم التطبيقات الأساسية لـ SVC و NuSVC مُولّد أرقام عشوائية فقط لخلط البيانات لتقدير الاحتمالية (عندما يتم تعيين probability إلى True). يمكن التحكم في هذه العشوائية باستخدام معلمة random_state. إذا تم تعيين probability إلى False، فإن هذه المقدرات ليست عشوائية وليس لـ random_state أي تأثير على النتائج. تطبيق OneClassSVM الأساسي مشابه لتطبيقات SVC و NuSVC. نظرًا لعدم توفير تقدير احتمالية لـ OneClassSVM، فهو ليس عشوائيًا.

    يستخدم تطبيق LinearSVC الأساسي مُولّد أرقام عشوائية لتحديد الميزات عند ملاءمة النموذج مع هبوط إحداثي مُزدوج (أي عندما يتم تعيين dual إلى True). وبالتالي، ليس من غير المألوف الحصول على نتائج مختلفة قليلاً لنفس بيانات الإدخال. إذا حدث ذلك، فجرب معلمة tol أصغر. يمكن أيضًا التحكم في هذه العشوائية باستخدام معلمة random_state. عندما يتم تعيين dual إلى False، فإن التطبيق الأساسي لـ LinearSVC ليس عشوائيًا وليس لـ random_state أي تأثير على النتائج.

  • يؤدي استخدام جزاء L1 كما هو مُقدّم بواسطة LinearSVC(penalty='l1', dual=False) إلى حل متفرق، أي أن مجموعة فرعية فقط من أوزان الميزات تختلف عن الصفر وتُساهم في دالة القرار. تؤدي زيادة C إلى نموذج أكثر تعقيدًا (يتم تحديد المزيد من الميزات). يمكن حساب قيمة C التي تُعطي نموذجًا "فارغًا" (جميع الأوزان تساوي صفرًا) باستخدام l1_min_c.

1.4.6. دوال النواة#

يمكن أن تكون دالة النواة أيًا مما يلي:

  • خطية: \(\langle x, x'\rangle\).

  • متعددة الحدود: \((\gamma \langle x, x'\rangle + r)^d\)، حيث يتم تحديد \(d\) بواسطة المعلمة degree، \(r\) بواسطة coef0.

  • rbf: \(\exp(-\gamma \|x-x'\|^2)\)، حيث يتم تحديد \(\gamma\) بواسطة المعلمة gamma، يجب أن تكون أكبر من 0.

  • السيني: \(\tanh(\gamma \langle x,x'\rangle + r)\)، حيث يتم تحديد \(r\) بواسطة coef0.

يتم تحديد نوى مختلفة بواسطة المعلمة kernel:

>>> linear_svc = svm.SVC(kernel='linear')
>>> linear_svc.kernel
'linear'
>>> rbf_svc = svm.SVC(kernel='rbf')
>>> rbf_svc.kernel
'rbf'

انظر أيضًا Kernel Approximation لحل لاستخدام نوى RBF أسرع وأكثر قابلية للتطوير.

1.4.6.1. معلمات نواة RBF#

عند تدريب SVM مع نواة دالة الأساس الشعاعي (RBF)، يجب مراعاة معلمتين: C و gamma. المعلمة C، الشائعة لجميع نوى SVM، تُوازن بين التصنيف الخاطئ لأمثلة التدريب وبساطة سطح القرار. C المنخفضة تجعل سطح القرار سلسًا، بينما تهدف C العالية إلى تصنيف جميع أمثلة التدريب بشكل صحيح. تُعرّف gamma مقدار تأثير مثال تدريب واحد. كلما زادت gamma، زادت قرب الأمثلة الأخرى لتتأثر.

الاختيار المناسب لـ C و gamma أمر بالغ الأهمية لأداء SVM. يُنصح باستخدام GridSearchCV مع C و gamma متباعدتين أسيًا لاختيار قيم جيدة.

أمثلة

1.4.6.2. نوى مخصصة#

يمكنك تعريف النوى الخاصة بك إما عن طريق إعطاء النواة كدالة بايثون أو عن طريق حساب مصفوفة غرام مُسبقًا.

تتصرف المُصنفات ذات النوى المخصصة بنفس طريقة أي مُصنفات أخرى، باستثناء:

  • الحقل support_vectors_ فارغ الآن، يتم تخزين مؤشرات متجهات الدعم فقط في support_

  • يتم تخزين مرجع (وليس نسخة) للوسيطة الأولى في طريقة fit() للرجوع إليها في المستقبل. إذا تغيرت تلك المصفوفة بين استخدام fit() و predict()، فستحصل على نتائج غير متوقعة.

استخدام دوال بايثون كنوى#

يمكنك استخدام النوى المُحدّدة الخاصة بك عن طريق تمرير دالة إلى المعلمة kernel.

يجب أن تأخذ نواتك مصفوفتين ذات شكل (n_samples_1, n_features) و (n_samples_2, n_features) كوسيطات وتُعيد مصفوفة نواة ذات شكل (n_samples_1, n_samples_2).

يُحدّد الكود التالي نواة خطية وينشئ مثيل مُصنف سيستخدم تلك النواة:

>>> import numpy as np
>>> from sklearn import svm
>>> def my_kernel(X, Y):
...     return np.dot(X, Y.T)
...
>>> clf = svm.SVC(kernel=my_kernel)
استخدام مصفوفة غرام#

يمكنك تمرير نوى محسوبة مُسبقًا باستخدام الخيار kernel='precomputed'. يجب عليك بعد ذلك تمرير مصفوفة غرام بدلاً من X إلى طريقتي fit و predict. يجب توفير قيم النواة بين جميع متجهات التدريب ومتجهات الاختبار:

>>> import numpy as np
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import svm
>>> X, y = make_classification(n_samples=10, random_state=0)
>>> X_train , X_test , y_train, y_test = train_test_split(X, y, random_state=0)
>>> clf = svm.SVC(kernel='precomputed')
>>> # حساب النواة الخطية
>>> gram_train = np.dot(X_train, X_train.T)
>>> clf.fit(gram_train, y_train)
SVC(kernel='precomputed')
>>> # التنبؤ بأمثلة التدريب
>>> gram_test = np.dot(X_test, X_train.T)
>>> clf.predict(gram_test)
array([0, 1, 0])

أمثلة

1.4.7. الصيغة الرياضية#

تنشئ آلة متجه الدعم مستوى فائق أو مجموعة من المستويات الفائقة في فضاء ذي أبعاد عالية أو لا نهائية، والتي يمكن استخدامها للتصنيف أو الانحدار أو مهام أخرى. بشكل حدسي، يتم تحقيق فصل جيد بواسطة المستوى الفائق الذي لديه أكبر مسافة إلى أقرب نقاط بيانات التدريب لأي فئة (ما يُسمى بالهامش الوظيفي)، لأنه بشكل عام كلما زاد الهامش، قل خطأ التعميم للمُصنف. يُظهر الشكل أدناه دالة القرار لمشكلة قابلة للفصل خطيًا، مع ثلاث عينات على حدود الهامش، تُسمى "متجهات الدعم":

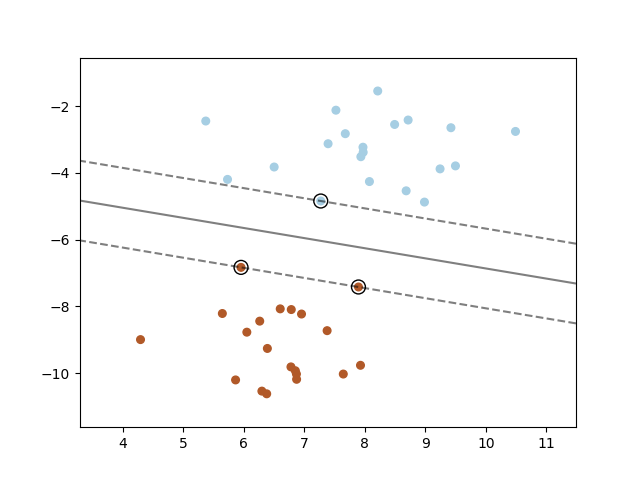
../_images/sphx_glr_plot_separating_hyperplane_001.png

بشكل عام، عندما لا تكون المشكلة قابلة للفصل خطيًا، فإن متجهات الدعم هي العينات ضمن حدود الهامش.

نُوصي بـ [13] و [14] كمراجع جيدة لنظرية SVM وتطبيقاتها العملية.

1.4.7.1. SVC#

بالنظر إلى متجهات التدريب \(x_i \in \mathbb{R}^p\)، i=1,..., n، في فئتين، ومتجه \(y \in \{1, -1\}^n\)، هدفنا هو إيجاد \(w \in \mathbb{R}^p\) و \(b \in \mathbb{R}\) بحيث يكون التنبؤ الذي قدمته \(\text{sign} (w^T\phi(x) + b)\) صحيحًا لمعظم العينات.

SVC تحل المشكلة الأساسية التالية:

\[ \begin{align}\begin{aligned}\min_ {w, b, \zeta} \frac{1}{2} w^T w + C \sum_{i=1}^{n} \zeta_i\\\begin{split}\textrm {subject to } & y_i (w^T \phi (x_i) + b) \geq 1 - \zeta_i,\\ & \zeta_i \geq 0, i=1, ..., n\end{split}\end{aligned}\end{align} \]

بشكل حدسي، نحاول تعظيم الهامش (عن طريق تصغير \(||w||^2 = w^Tw\))، مع تكبد عقوبة عندما يتم تصنيف عينة بشكل خاطئ أو ضمن حدود الهامش. من الناحية المثالية، ستكون قيمة \(y_i (w^T \phi (x_i) + b)\) هي \(\geq 1\) لجميع العينات، مما يشير إلى تنبؤ مثالي. لكن المشاكل عادةً ما تكون غير قابلة للفصل بشكل مثالي باستخدام مستوى فائق، لذلك نسمح لبعض العينات بأن تكون على مسافة \(\zeta_i\) من حدود الهامش الصحيحة. يتحكم مصطلح الجزاء C في قوة هذه العقوبة، ونتيجة لذلك، يعمل كمعلمة تنظيم عكسي (انظر الملاحظة أدناه).

المشكلة المزدوجة للمشكلة الأساسية هي

\[ \begin{align}\begin{aligned}\min_{\alpha} \frac{1}{2} \alpha^T Q \alpha - e^T \alpha\\\begin{split} \textrm {subject to } & y^T \alpha = 0\\ & 0 \leq \alpha_i \leq C, i=1, ..., n\end{split}\end{aligned}\end{align} \]

حيث \(e\) هو متجه كل الآحاد، \(Q\) هي مصفوفة شبه موجبة \(n\) في \(n\)، \(Q_{ij} \equiv y_i y_j K(x_i, x_j)\)، حيث \(K(x_i, x_j) = \phi (x_i)^T \phi (x_j)\) هي النواة. تُسمى المصطلحات \(\alpha_i\) المعاملات المزدوجة، وهي مُحدّدة بحد أعلى \(C\). يُبرز هذا التمثيل المزدوج حقيقة أن متجهات التدريب يتم تعيينها ضمنيًا في فضاء ذي أبعاد أعلى (ربما لانهائية) بواسطة الدالة \(\phi\): انظر خدعة النواة.

بمجرد حل مشكلة التحسين، يُصبح ناتج decision_function لعينة مُعطاة \(x\) هو:

\[\sum_{i\in SV} y_i \alpha_i K(x_i, x) + b,\]

وتتوافق الفئة المتوقعة مع علامتها. نحتاج فقط إلى الجمع على متجهات الدعم (أي العينات التي تقع داخل الهامش) لأن المعاملات المزدوجة \(\alpha_i\) تساوي صفرًا للعينات الأخرى.

يمكن الوصول إلى هذه المعلمات من خلال السمات dual_coef_ التي تحتوي على حاصل الضرب \(y_i \alpha_i\)، support_vectors_ التي تحتوي على متجهات الدعم، و intercept_ التي تحتوي على المصطلح المستقل \(b\).

ملاحظة

بينما تستخدم نماذج SVM المُشتقة من libsvm و liblinear C كمعلمة تنظيم، فإن معظم المقدرات الأخرى تستخدم alpha. تعتمد التكافؤ الدقيق بين مقدار تنظيم نموذجين على دالة الهدف الدقيقة التي تم تحسينها بواسطة النموذج. على سبيل المثال، عندما يكون المقدّر المستخدم هو انحدار Ridge، فإن العلاقة بينهما تُعطى على أنها \(C = \frac{1}{alpha}\).

LinearSVC#

يمكن صياغة المشكلة الأساسية بشكل مُكافئ على النحو التالي:

\[\min_ {w, b} \frac{1}{2} w^T w + C \sum_{i=1}^{n}\max(0, 1 - y_i (w^T \phi(x_i) + b)),\]

حيث نستخدم خسارة المفصلة. هذا هو الشكل الذي تم تحسينه مُباشرةً بواسطة LinearSVC، ولكن على عكس الشكل المزدوج، لا يتضمن هذا الشكل حاصل الضرب الداخلي بين العينات، لذلك لا يمكن تطبيق خدعة النواة الشهيرة. هذا هو السبب في أن النواة الخطية فقط مدعومة بواسطة LinearSVC (\(\phi\) هي دالة الهوية).

NuSVC#

صيغة \(\nu\)-SVC [15] هي إعادة تحديد معلمات لـ \(C\)-SVC، وبالتالي فهي مكافئة رياضيًا.

نُقدّم معلمة جديدة \(\nu\) (بدلاً من \(C\)) التي تتحكم في عدد متجهات الدعم و أخطاء الهامش: \(\nu \in (0, 1]\) هو حد أعلى لكسر أخطاء الهامش وحد أدنى لكسر متجهات الدعم. يتوافق خطأ الهامش مع عينة تقع على الجانب الخطأ من حدود هامشها: إما أنها مُصنّفة بشكل خاطئ، أو أنها مُصنّفة بشكل صحيح ولكنها لا تقع خارج الهامش.

1.4.7.2. SVR#

بالنظر إلى متجهات التدريب \(x_i \in \mathbb{R}^p\)، i=1,..., n، ومتجه \(y \in \mathbb{R}^n\)، فإن \(\varepsilon\)-SVR يحل المشكلة الأساسية التالية:

\[ \begin{align}\begin{aligned}\min_ {w, b, \zeta, \zeta^*} \frac{1}{2} w^T w + C \sum_{i=1}^{n} (\zeta_i + \zeta_i^*)\\\begin{split}\textrm {subject to } & y_i - w^T \phi (x_i) - b \leq \varepsilon + \zeta_i,\\ & w^T \phi (x_i) + b - y_i \leq \varepsilon + \zeta_i^*,\\ & \zeta_i, \zeta_i^* \geq 0, i=1, ..., n\end{split}\end{aligned}\end{align} \]

هنا، نُعاقب العينات التي يكون تنبؤها على الأقل \(\varepsilon\) بعيدًا عن هدفها الحقيقي. تُعاقب هذه العينات الهدف بواسطة \(\zeta_i\) أو \(\zeta_i^*\)، اعتمادًا على ما إذا كانت تنبؤاتها تقع فوق أو أسفل أنبوب \(\varepsilon\).

المشكلة المزدوجة هي

\[ \begin{align}\begin{aligned}\min_{\alpha, \alpha^*} \frac{1}{2} (\alpha - \alpha^*)^T Q (\alpha - \alpha^*) + \varepsilon e^T (\alpha + \alpha^*) - y^T (\alpha - \alpha^*)\\\begin{split} \textrm {subject to } & e^T (\alpha - \alpha^*) = 0\\ & 0 \leq \alpha_i, \alpha_i^* \leq C, i=1, ..., n\end{split}\end{aligned}\end{align} \]

حيث \(e\) هو متجه كل الآحاد، \(Q\) هي مصفوفة شبه موجبة \(n\) في \(n\)، \(Q_{ij} \equiv K(x_i, x_j) = \phi (x_i)^T \phi (x_j)\) هي النواة. هنا يتم تعيين متجهات التدريب ضمنيًا في فضاء ذي أبعاد أعلى (ربما لانهائية) بواسطة الدالة \(\phi\).

التنبؤ هو:

\[\sum_{i \in SV}(\alpha_i - \alpha_i^*) K(x_i, x) + b\]

يمكن الوصول إلى هذه المعلمات من خلال السمات dual_coef_ التي تحتوي على الفرق \(\alpha_i - \alpha_i^*\)، support_vectors_ التي تحتوي على متجهات الدعم، و intercept_ التي تحتوي على المصطلح المستقل \(b\).

LinearSVR#

يمكن صياغة المشكلة الأساسية بشكل مُكافئ على النحو التالي:

\[\min_ {w, b} \frac{1}{2} w^T w + C \sum_{i=1}^{n}\max(0, |y_i - (w^T \phi(x_i) + b)| - \varepsilon),\]

حيث نستخدم خسارة غير حساسة لأبسيلون، أي يتم تجاهل الأخطاء الأقل من \(\varepsilon\). هذا هو الشكل الذي تم تحسينه مُباشرةً بواسطة LinearSVR.

1.4.8. تفاصيل التطبيق#

داخليًا، نستخدم libsvm [12] و liblinear [11] للتعامل مع جميع الحسابات. يتم تغليف هذه المكتبات باستخدام C و Cython. للحصول على وصف للتطبيق وتفاصيل الخوارزميات المستخدمة، يرجى الرجوع إلى أوراقهما الخاصة.

المراجع