2.2. تعلم المشعبات

Look for the bare necessities

The simple bare necessities

Forget about your worries and your strife

I mean the bare necessities

Old Mother Nature's recipes

That bring the bare necessities of life

-- Baloo's song [The Jungle Book]

تعلم المشعبات هو نهج للاختزال غير الخطي للأبعاد. تعتمد خوارزميات هذه المهمة على فكرة أن أبعاد العديد من مجموعات البيانات مرتفعة بشكل مصطنع فقط.

2.2.1. مقدمة

يمكن أن تكون مجموعات البيانات عالية الأبعاد صعبة التصور للغاية. في حين أنه يمكن رسم البيانات في بعدين أو ثلاثة أبعاد لإظهار البنية المتأصلة للبيانات، فإن الرسوم البيانية عالية الأبعاد المكافئة تكون أقل سهولة بكثير. لمساعدة تصور بنية مجموعة البيانات، يجب تقليل البعد بطريقة ما.

أبسط طريقة لإنجاز هذا الاختزال للأبعاد هي عن طريق أخذ إسقاط عشوائي للبيانات. على الرغم من أن هذا يسمح بدرجة معينة من تصور بنية البيانات، فإن عشوائية الاختيار تترك الكثير مما هو مرغوب فيه. في الإسقاط العشوائي، من المحتمل أن تُفقد البنية الأكثر إثارة للاهتمام داخل البيانات.

لمعالجة هذا القلق، تم تصميم عدد من أطر الاختزال الخطي للأبعاد الخاضعة للإشراف وغير الخاضعة للإشراف، مثل تحليل المكونات الرئيسية (PCA) وتحليل المكونات المستقلة والتحليل التمييزي الخطي وغيرها. تحدد هذه الخوارزميات معايير محددة لاختيار إسقاط خطي "مثير للاهتمام" للبيانات. يمكن أن تكون هذه الطرق قوية، ولكنها غالبًا ما تفقد بنية غير خطية مهمة في البيانات.

يمكن اعتبار تعلم المشعبات محاولة لتعميم الأطر الخطية مثل PCA لتكون حساسة للبنية غير الخطية في البيانات. على الرغم من وجود متغيرات خاضعة للإشراف، فإن مشكلة تعلم المشعبات النموذجية تكون غير خاضعة للإشراف: فهي تتعلم البنية عالية الأبعاد للبيانات من البيانات نفسها، دون استخدام تصنيفات محددة مسبقًا.

أمثلة

• انظر تعلم متعدد الشعب على الأرقام المكتوبة بخط اليد: التضمين الخطي المحلي، Isomap... للحصول على مثال على اختزال الأبعاد على الأرقام المكتوبة بخط اليد.

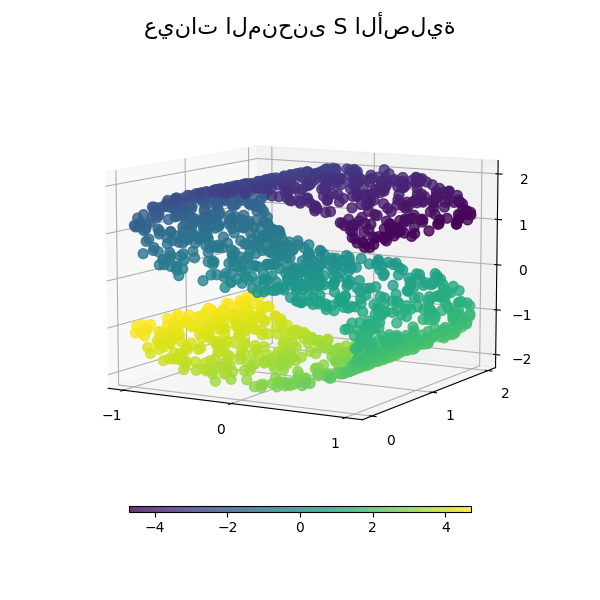
• انظر مقارنة طرق تعلم متعدد الشعب للحصول على مثال على اختزال الأبعاد على مجموعة بيانات "منحنى S" تجريبية.

• انظر هيكلة سوق الأسهم المرئية للحصول على مثال على استخدام تعلم المشعبات لرسم خريطة بنية سوق الأسهم بناءً على أسعار الأسهم التاريخية.

يتم تلخيص تطبيقات تعلم المشعبات المتوفرة في scikit-learn أدناه

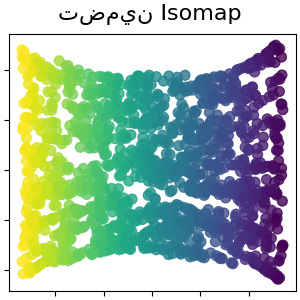
2.2.2. Isomap

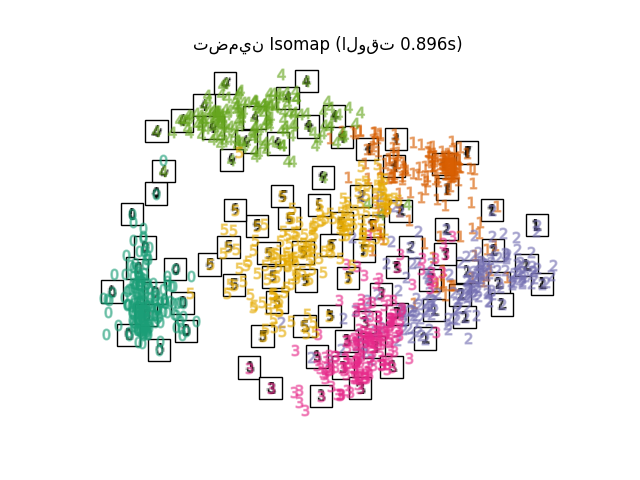
أحد أقدم أساليب تعلم المشعبات هو خوارزمية Isomap، وهي اختصار لـ Isometric Mapping. يمكن اعتبار Isomap امتدادًا للتحجيم متعدد الأبعاد (MDS) أو Kernel PCA. يبحث Isomap عن تضمين أقل أبعادًا يحافظ على المسافات الجيوديسية بين جميع النقاط. يمكن إجراء Isomap باستخدام الكائن Isomap.

التعقيد

تتكون خوارزمية Isomap من ثلاث مراحل:

1. بحث أقرب جار. يستخدم Isomap BallTree للبحث الفعال عن الجيران. التكلفة هي تقريبًا \(O[D \log(k) N \log(N)]\)، لـ \(k\) من أقرب جيران \(N\) نقاط في \(D\) أبعاد.

2. بحث أقصر مسار في الرسم البياني. الخوارزميات الأكثر كفاءة المعروفة لهذا هي خوارزمية Dijkstra، والتي هي تقريبًا \(O[N^2(k + \log(N))]\)، أو خوارزمية Floyd-Warshall، وهي \(O[N^3]\). يمكن للمستخدم تحديد الخوارزمية باستخدام الكلمة المفتاحية path_method من Isomap. إذا لم يتم التحديد، تحاول الشيفرة اختيار أفضل خوارزمية لبيانات الإدخال.

3. التحليل الجزئي لقيم eigenvalues. يتم ترميز التضمين في المتجهات الذاتية المقابلة لـ \(d\) أكبر قيم eigenvalues لنواة isomap \(N \times N\). بالنسبة لحلال كثيف، فإن التكلفة هي تقريبًا \(O[d N^2]\). غالبًا ما يمكن تحسين هذه التكلفة باستخدام محلل ARPACK. يمكن للمستخدم تحديد محلل eigen باستخدام الكلمة المفتاحية eigen_solver من Isomap. إذا لم يتم التحديد، تحاول الشيفرة اختيار أفضل خوارزمية لبيانات الإدخال.

التعقيد الكلي لـ Isomap هو \(O[D \log(k) N \log(N)] + O[N^2(k + \log(N))] + O[d N^2]\).

• \(N\) : عدد نقاط بيانات التدريب

• \(D\) : بُعد الإدخال

• \(k\) : عدد أقرب جيران

• \(d\) : بُعد الإخراج

المراجع

• "A global geometric framework for nonlinear dimensionality reduction" Tenenbaum, J.B.; De Silva, V.; & Langford, J.C. Science 290 (5500)

2.2.3. Locally Linear Embedding (التضمين الخطي المحلي)

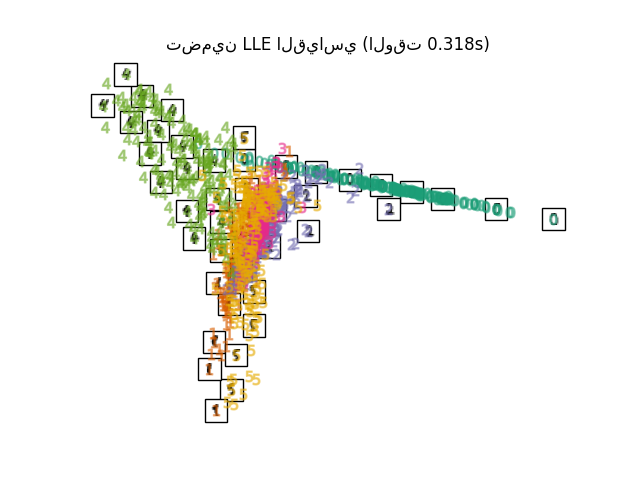
يسعى التضمين الخطي المحلي (LLE) إلى إسقاط ذي أبعاد منخفضة للبيانات والذي يحافظ على المسافات داخل الأحياء المحلية. يمكن اعتباره سلسلة من تحليلات المكونات الرئيسية المحلية التي تتم مقارنتها عالميًا للعثور على أفضل تضمين غير خطي.

يمكن تنفيذ التضمين الخطي المحلي باستخدام الدالة locally_linear_embedding أو نظيرتها الكائنية التوجه LocallyLinearEmbedding.

التعقيد

تتكون خوارزمية LLE القياسية من ثلاث مراحل:

1. بحث أقرب جار. انظر المناقشة تحت Isomap أعلاه.

2. بناء مصفوفة الوزن. \(O[D N k^3]\). يتضمن بناء مصفوفة الوزن LLE حل معادلة خطية \(k \times k\) لكل من الأحياء المحلية \(N\).

3. التحليل الجزئي لقيم eigenvalues. انظر المناقشة تحت Isomap أعلاه.

التعقيد الكلي لـ LLE القياسي هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).

• \(N\) : عدد نقاط بيانات التدريب

• \(D\) : بُعد الإدخال

• \(k\) : عدد أقرب جيران

• \(d\) : بُعد الإخراج

المراجع

• "Nonlinear dimensionality reduction by locally linear embedding" Roweis, S. & Saul, L. Science 290:2323 (2000)

2.2.4. Modified Locally Linear Embedding (التضمين الخطي المحلي المعدل)

إحدى المشكلات المعروفة في LLE هي مشكلة التنظيم. عندما يكون عدد الجيران أكبر من عدد أبعاد الإدخال، فإن المصفوفة التي تحدد كل جيرة محلية تكون ناقصة الرتبة. لمعالجة هذا، يطبق LLE القياسي معامل تنظيم عشوائي \(r\)، والذي يتم اختياره بالنسبة إلى أثر مصفوفة الوزن المحلي. على الرغم من أنه يمكن إثباته رسميًا أنه عندما \(r \to 0\)، يتقارب الحل مع التضمين المطلوب، فلا يوجد ضمان بأن الحل الأمثل سيوجد لـ \(r > 0\). تتجلى هذه المشكلة في التضمينات التي تشوه الهندسة الأساسية للمشعب.

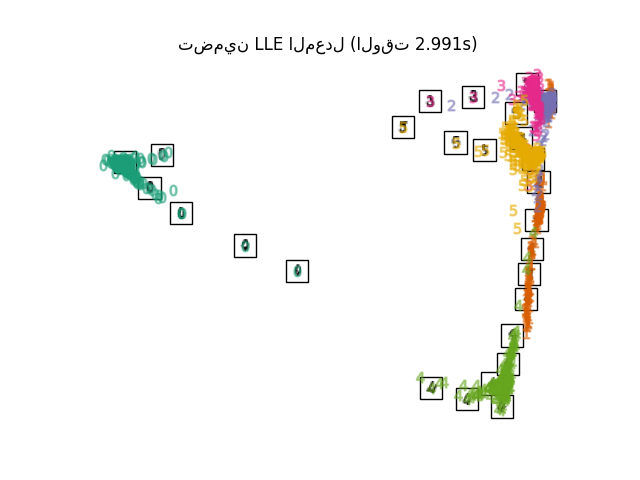
إحدى طرق معالجة مشكلة التنظيم هي استخدام متجهات وزن متعددة في كل جيرة. هذا هو جوهر التضمين الخطي المحلي المعدل (MLLE). يمكن تنفيذ MLLE باستخدام الدالة locally_linear_embedding أو نظيرتها الكائنية التوجه LocallyLinearEmbedding، مع الكلمة المفتاحية method = 'modified'. يتطلب n_neighbors > n_components.

التعقيد

تتكون خوارزمية MLLE من ثلاث مراحل:

1. بحث أقرب جار. نفس LLE القياسي

2. بناء مصفوفة الوزن. تقريبًا \(O[D N k^3] + O[N (k-D) k^2]\). المصطلح الأول مكافئ تمامًا لمصطلح LLE القياسي. المصطلح الثاني له علاقة ببناء مصفوفة الوزن من أوزان متعددة. من الناحية العملية، فإن التكلفة الإضافية لبناء مصفوفة وزن MLLE صغيرة نسبيًا مقارنة بتكلفة المرحلتين 1 و 3.

3. التحليل الجزئي لقيم eigenvalues. نفس LLE القياسي

التعقيد الكلي لـ MLLE هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N (k-D) k^2] + O[d N^2]\).

• \(N\) : عدد نقاط بيانات التدريب

• \(D\) : بُعد الإدخال

• \(k\) : عدد أقرب جيران

• \(d\) : بُعد الإخراج

المراجع

• "MLLE: Modified Locally Linear Embedding Using Multiple Weights" Zhang, Z. & Wang, J.

2.2.5. Hessian Eigenmapping (تعيين Eigen Hessian)

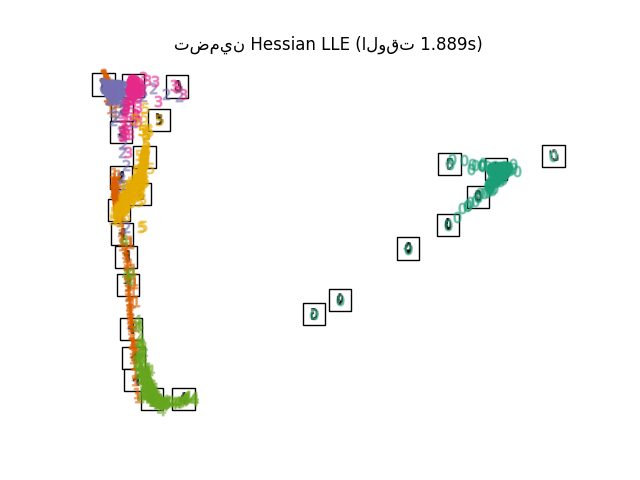
Hessian Eigenmapping (المعروف أيضًا باسم HLLE القائم على Hessian) هو طريقة أخرى لحل مشكلة التنظيم في LLE. يدور حول شكل تربيعي قائم على Hessian في كل جيرة والذي يُستخدم لاستعادة البنية الخطية محليًا. على الرغم من أن التطبيقات الأخرى تشير إلى تحجيمه الضعيف مع حجم البيانات، فإن sklearn تُطبق بعض التحسينات الخوارزمية التي تجعل تكلفتها مماثلة لتلك الخاصة بمتغيرات LLE الأخرى لبُعد إخراج صغير. يمكن تنفيذ HLLE باستخدام الدالة locally_linear_embedding أو نظيرتها الكائنية التوجه LocallyLinearEmbedding، مع الكلمة المفتاحية method = 'hessian'. يتطلب n_neighbors > n_components * (n_components + 3) / 2.

التعقيد

تتكون خوارزمية HLLE من ثلاث مراحل:

1. بحث أقرب جار. نفس LLE القياسي

2. بناء مصفوفة الوزن. تقريبًا \(O[D N k^3] + O[N d^6]\). يعكس المصطلح الأول تكلفة مماثلة لتلك الخاصة بـ LLE القياسي. المصطلح الثاني يأتي من تحليل QR لمقدر Hessian المحلي.

3. التحليل الجزئي لقيم eigenvalues. نفس LLE القياسي

التعقيد الكلي لـ HLLE القياسي هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N d^6] + O[d N^2]\).

• \(N\) : عدد نقاط بيانات التدريب

• \(D\) : بُعد الإدخال

• \(k\) : عدد أقرب جيران

• \(d\) : بُعد الإخراج

المراجع

• "Hessian Eigenmaps: Locally linear embedding techniques for high-dimensional data" Donoho, D. & Grimes, C. Proc Natl Acad Sci USA. 100:5591 (2003)

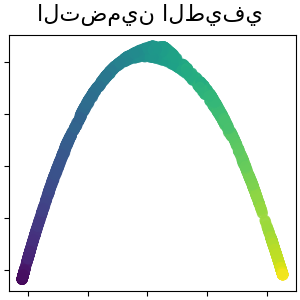
2.2.6. Spectral Embedding (التضمين الطيفي)

التضمين الطيفي هو نهج لحساب تضمين غير خطي. تُطبق Scikit-learn خرائط Laplacian Eigenmaps، والتي تجد تمثيلًا ذي أبعاد منخفضة للبيانات باستخدام تحليل طيفي لـ Laplacian الرسم البياني. يمكن اعتبار الرسم البياني الذي تم إنشاؤه بمثابة تقريب منفصل للمشعب ذي الأبعاد المنخفضة في الفضاء ذي الأبعاد العالية. يضمن تصغير دالة التكلفة بناءً على الرسم البياني أن النقاط القريبة من بعضها البعض على المشعب يتم تعيينها بالقرب من بعضها البعض في الفضاء ذي الأبعاد المنخفضة، مع الحفاظ على المسافات المحلية. يمكن تنفيذ التضمين الطيفي باستخدام الدالة spectral_embedding أو نظيرتها الكائنية التوجه SpectralEmbedding.

التعقيد

تتكون خوارزمية التضمين الطيفي (Laplacian Eigenmaps) من ثلاث مراحل:

1. بناء الرسم البياني الموزون. تحويل بيانات الإدخال الأولية إلى تمثيل بياني باستخدام تمثيل مصفوفة التقارب (التجاور).

2. بناء Laplacian الرسم البياني. يتم بناء Laplacian الرسم البياني غير المعياري على النحو التالي \(L = D - A\) ويتم بناء Laplacian الرسم البياني المعياري على النحو التالي \(L = D^{-\frac{1}{2}} (D - A) D^{-\frac{1}{2}}\).

3. التحليل الجزئي لقيم eigenvalues. يتم إجراء تحليل قيم eigenvalues على Laplacian الرسم البياني.

التعقيد الكلي للتضمين الطيفي هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).

• \(N\) : عدد نقاط بيانات التدريب

• \(D\) : بُعد الإدخال

• \(k\) : عدد أقرب جيران

• \(d\) : بُعد الإخراج

المراجع

• "Laplacian Eigenmaps for Dimensionality Reduction and Data Representation" M. Belkin, P. Niyogi, Neural Computation, June 2003; 15 (6):1373-1396

2.2.7. Local Tangent Space Alignment (محاذاة فضاء المماس المحلي)

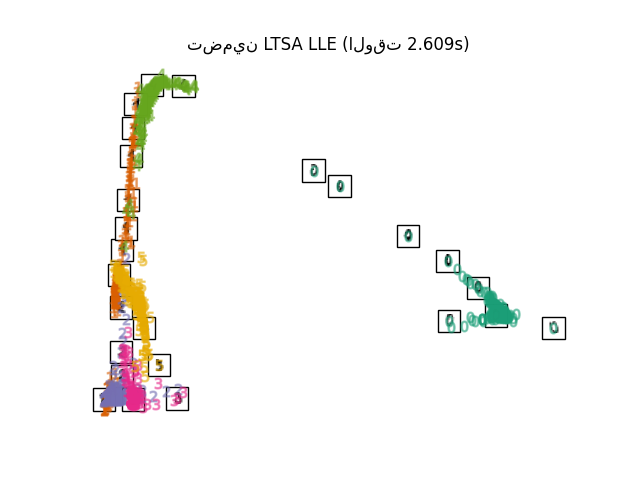
على الرغم من أنها ليست من الناحية الفنية متغيرًا من LLE، فإن محاذاة فضاء المماس المحلي (LTSA) تشبه خوارزميًا LLE بما يكفي لوضعها في هذه الفئة. بدلاً من التركيز على الحفاظ على مسافات الجيرة كما هو الحال في LLE، تسعى LTSA إلى توصيف الهندسة المحلية عند كل جيرة من خلال مساحة المماس الخاصة بها، وتجري تحسينًا عالميًا لمحاذاة مساحات المماس المحلية هذه لتعلم التضمين. يمكن تنفيذ LTSA باستخدام الدالة locally_linear_embedding أو نظيرتها الكائنية التوجه LocallyLinearEmbedding، مع الكلمة المفتاحية method = 'ltsa'.

التعقيد

تتكون خوارزمية LTSA من ثلاث مراحل:

1. بحث أقرب جار. نفس LLE القياسي

2. بناء مصفوفة الوزن. تقريبًا \(O[D N k^3] + O[k^2 d]\). يعكس المصطلح الأول تكلفة مماثلة لتلك الخاصة بـ LLE القياسي.

3. التحليل الجزئي لقيم eigenvalues. نفس LLE القياسي

التعقيد الكلي لـ LTSA القياسي هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[k^2 d] + O[d N^2]\).

• \(N\) : عدد نقاط بيانات التدريب

• \(D\) : بُعد الإدخال

• \(k\) : عدد أقرب جيران

• \(d\) : بُعد الإخراج

المراجع

• "Principal manifolds and nonlinear dimensionality reduction via tangent space alignment" Zhang, Z. & Zha, H. Journal of Shanghai Univ. 8:406 (2004)

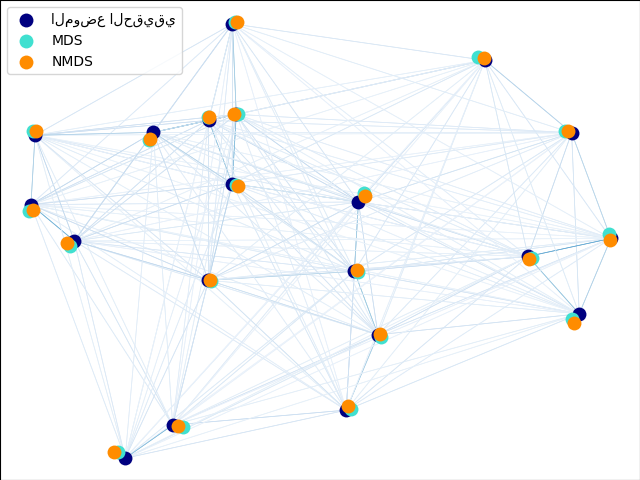
2.2.8. Multi-dimensional Scaling (MDS) (التحجيم متعدد الأبعاد)

التحجيم متعدد الأبعاد (MDS) يبحث عن تمثيل ذي أبعاد منخفضة للبيانات حيث تحترم المسافات بشكل جيد المسافات في الفضاء الأصلي ذي الأبعاد العالية.

بشكل عام، MDS هي تقنية تُستخدم لتحليل بيانات التشابه أو الاختلاف. تحاول نمذجة بيانات التشابه أو الاختلاف كمسافات في مساحات هندسية. يمكن أن تكون البيانات عبارة عن تقييمات للتشابه بين الكائنات، أو ترددات تفاعل الجزيئات، أو مؤشرات التجارة بين البلدان.

يوجد نوعان من خوارزمية MDS: مترية وغير مترية. في scikit-learn، تُطبق الفئة MDS كليهما. في MDS المتري، تنشأ مصفوفة التشابه المدخلة من مقياس (وبالتالي تحترم متباينة المثلث)، ثم يتم ضبط المسافات بين نقطتي إخراج لتكون أقرب ما يمكن لبيانات التشابه أو الاختلاف. في الإصدار غير المتري، ستحاول الخوارزميات الحفاظ على ترتيب المسافات، وبالتالي البحث عن علاقة رتيبة بين المسافات في الفضاء المضمن والتشابهات/الاختلافات.

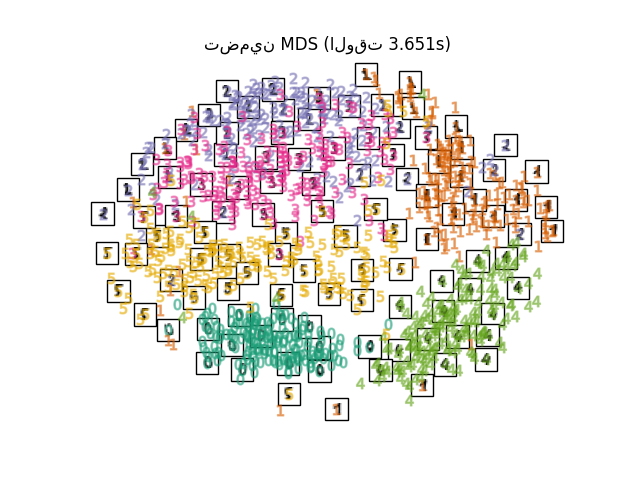
دع \(S\) تكون مصفوفة التشابه، و \(X\) إحداثيات \(n\) نقاط الإدخال. التباينات \(\hat{d}_{ij}\) هي تحويل للتشابهات المختارة ببعض الطرق المثلى. يتم بعد ذلك تحديد الهدف، المسمى الإجهاد، بواسطة \(\sum_{i < j} d_{ij}(X) - \hat{d}_{ij}(X)\)

MDS المتري

أبسط نموذج MDS متري، يسمى MDS المطلق، يتم تعريف التباينات بواسطة \(\hat{d}_{ij} = S_{ij}\). باستخدام MDS المطلق، يجب أن تتوافق القيمة \(S_{ij}\) تمامًا مع المسافة بين النقطة \(i\) والنقطة \(j\) في نقطة التضمين.

في أغلب الأحيان، يتم تعيين التباينات على \(\hat{d}_{ij} = b S_{ij}\).

MDS غير المتري

يركز MDS غير المتري على ترتيب البيانات. إذا \(S_{ij} > S_{jk}\)، فيجب أن يفرض التضمين \(d_{ij} < d_{jk}\). لهذا السبب، نناقشه من حيث الاختلافات (\(\delta_{ij}\)) بدلاً من التشابهات (\(S_{ij}\)). لاحظ أنه يمكن الحصول على الاختلافات بسهولة من التشابهات من خلال تحويل بسيط، على سبيل المثال \(\delta_{ij}=c_1-c_2 S_{ij}\) لبعض الثوابت الحقيقية \(c_1, c_2\). تتمثل إحدى الخوارزميات البسيطة لفرض الترتيب المناسب في استخدام انحدار رتيب لـ \(d_{ij}\) على \(\delta_{ij}\)، مما ينتج عنه تباينات \(\hat{d}_{ij}\) بنفس ترتيب \(\delta_{ij}\).

الحل التافه لهذه المشكلة هو تعيين جميع النقاط على الأصل. لتجنب ذلك، يتم تطبيع التباينات \(\hat{d}_{ij}\). لاحظ أنه نظرًا لأننا نهتم فقط بالترتيب النسبي، فيجب أن يكون هدفنا ثابتًا بالنسبة للترجمة والتحجيم البسيطين، ومع ذلك فإن الإجهاد المستخدم في MDS المتري حساس للتحجيم. لمعالجة هذا، قد يستخدم MDS غير المتري إجهادًا معياريًا، يُعرف باسم Stress-1 والذي يُعرّف على النحو التالي

\[\sqrt{\frac{\sum_{i < j} (d_{ij} - \hat{d}_{ij})^2}{\sum_{i < j} d_{ij}^2}}.\]

يمكن تمكين استخدام Stress-1 المعياري عن طريق تعيين normalized_stress=True، ومع ذلك فهو متوافق فقط مع مشكلة MDS غير المترية وسيتم تجاهله في الحالة المترية.

المراجع

• "Modern Multidimensional Scaling - Theory and Applications" Borg, I.; Groenen P. Springer Series in Statistics (1997)

• "Nonmetric multidimensional scaling: a numerical method" Kruskal, J. Psychometrika, 29 (1964)

• "Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis" Kruskal, J. Psychometrika, 29, (1964)

2.2.9. t-distributed Stochastic Neighbor Embedding (t-SNE) (التضمين العشوائي للجار الموزع على t)

يحول t-SNE (TSNE) تقاربات نقاط البيانات إلى احتمالات. يتم تمثيل التقاربات في الفضاء الأصلي بواسطة احتمالات جاوس المشتركة ويتم تمثيل التقاربات في الفضاء المضمن بواسطة توزيعات t للطالب. وهذا يسمح لـ t-SNE بأن يكون حساسًا بشكل خاص للبنية المحلية وله عدد قليل من المزايا الأخرى على التقنيات الحالية:

• الكشف عن البنية على العديد من المقاييس على خريطة واحدة

• الكشف عن البيانات التي تقع في مشعبات أو مجموعات متعددة ومختلفة

• تقليل ميل حشد النقاط معًا في المركز

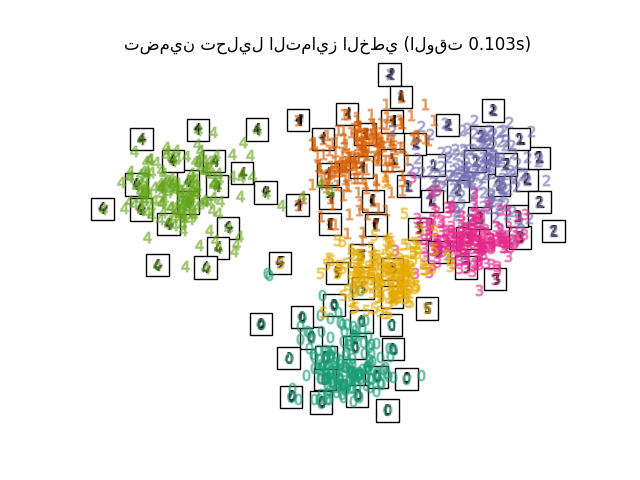
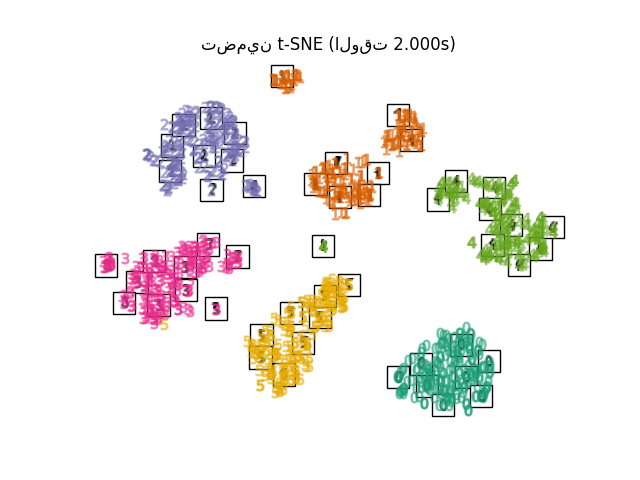
في حين أن Isomap و LLE والمتغيرات مناسبة بشكل أفضل لفك مشعب منخفض الأبعاد واحد مستمر، سيركز t-SNE على البنية المحلية للبيانات وسيميل إلى استخراج مجموعات محلية مجمعة من العينات كما هو موضح في مثال منحنى S. قد تكون هذه القدرة على تجميع العينات بناءً على البنية المحلية مفيدة لفك تشابك مجموعة بيانات تضم العديد من المشعبات في وقت واحد كما هو الحال في مجموعة بيانات الأرقام بصريًا.

سيتم تقليل اختلاف Kullback-Leibler (KL) للاحتمالات المشتركة في الفضاء الأصلي والفضاء المضمن عن طريق الانحدار التدريجي. لاحظ أن اختلاف KL ليس محدبًا، أي أن عمليات إعادة التشغيل المتعددة ذات التهيئات المختلفة ستنتهي في الحدود الدنيا المحلية لاختلاف KL. ومن ثم، من المفيد أحيانًا تجربة بذور مختلفة وتحديد التضمين مع أقل اختلاف KL.

عيوب استخدام t-SNE هي تقريبًا:

• t-SNE مكلف حسابيًا، ويمكن أن يستغرق عدة ساعات على مجموعات البيانات المكونة من مليون عينة حيث سينتهي PCA في ثوانٍ أو دقائق

• طريقة Barnes-Hut t-SNE مقتصرة على تضمينات ثنائية أو ثلاثية الأبعاد.

• الخوارزمية عشوائية ويمكن أن تؤدي عمليات إعادة التشغيل المتعددة ببذور مختلفة إلى تضمينات مختلفة. ومع ذلك، فمن المشروع تمامًا اختيار التضمين بأقل خطأ.

• لا يتم الحفاظ على البنية العامة بشكل صريح. يتم التخفيف من هذه المشكلة عن طريق تهيئة النقاط باستخدام PCA (باستخدام init='pca').

تحسين t-SNE

الغرض الرئيسي من t-SNE هو تصور البيانات عالية الأبعاد. ومن ثم، فإنه يعمل بشكل أفضل عندما يتم تضمين البيانات في بعدين أو ثلاثة أبعاد.

قد يكون تحسين اختلاف KL صعبًا بعض الشيء في بعض الأحيان. هناك خمس معلمات تتحكم في تحسين t-SNE وبالتالي ربما جودة التضمين الناتج:

• التعقيد

• عامل المبالغة المبكرة

• معدل التعلم

• الحد الأقصى لعدد التكرارات

• الزاوية (لا تُستخدم في الطريقة الدقيقة)

يُعرّف التعقيد بأنه \(k=2^{(S)}\) حيث \(S\) هو إنتروبيا شانون لتوزيع الاحتمال الشرطي. تعقيد حجر النرد ذي \(k\) جانب هو \(k\)، بحيث يكون \(k\) بشكل فعال عدد أقرب الجيران الذي يعتبره t-SNE عند توليد الاحتمالات الشرطية. تؤدي التعقيدات الأكبر إلى المزيد من أقرب الجيران وأقل حساسية للبنية الصغيرة. وعلى العكس من ذلك، يعتبر التعقيد المنخفض عددًا أقل من الجيران، وبالتالي يتجاهل المزيد من المعلومات العالمية لصالح الحي المحلي. مع ازدياد أحجام مجموعات البيانات، ستكون هناك حاجة إلى المزيد من النقاط للحصول على عينة معقولة من الحي المحلي، وبالتالي قد تكون هناك حاجة إلى تعقيدات أكبر. وبالمثل، ستتطلب مجموعات البيانات الأكثر ضوضاء قيم تعقيد أكبر لتشمل عددًا كافيًا من الجيران المحليين لرؤية ما وراء ضوضاء الخلفية.

الحد الأقصى لعدد التكرارات عادة ما يكون مرتفعًا بما يكفي ولا يحتاج إلى أي ضبط. يتكون التحسين من مرحلتين: مرحلة المبالغة المبكرة والتحسين النهائي. أثناء المبالغة المبكرة، سيتم زيادة الاحتمالات المشتركة في الفضاء الأصلي بشكل مصطنع عن طريق الضرب في عامل معين. تؤدي العوامل الأكبر إلى فجوات أكبر بين المجموعات الطبيعية في البيانات. إذا كان العامل مرتفعًا جدًا، فقد يزداد اختلاف KL خلال هذه المرحلة. عادة لا يلزم ضبطه. معلمة حرجة هي معدل التعلم. إذا كان منخفضًا جدًا، فسوف يعلق الانحدار التدريجي في حد أدنى محلي سيئ. إذا كان مرتفعًا جدًا، فسوف يزداد اختلاف KL أثناء التحسين. تتمثل الإرشادية المقترحة في Belkina et al. (2019) في تعيين معدل التعلم على حجم العينة مقسومًا على عامل المبالغة المبكرة. نُطبق هذه الإرشادية كوسيطة learning_rate='auto'. يمكن العثور على المزيد من النصائح في الأسئلة الشائعة لورانس فان دير مايتن (انظر المراجع). المعلمة الأخيرة، الزاوية، هي مفاضلة بين الأداء والدقة. الزوايا الأكبر تعني أنه يمكننا تقريب مناطق أكبر بنقطة واحدة، مما يؤدي إلى سرعة أفضل ولكن نتائج أقل دقة.

يوفر "How to Use t-SNE Effectively" مناقشة جيدة لتأثيرات المعلمات المختلفة، بالإضافة إلى مخططات تفاعلية لاستكشاف تأثيرات المعلمات المختلفة.

Barnes-Hut t-SNE

عادة ما يكون Barnes-Hut t-SNE الذي تم تنفيذه هنا أبطأ بكثير من خوارزميات تعلم المشعبات الأخرى. التحسين صعب للغاية وحساب التدرج هو \(O[d N log(N)]\)، حيث \(d\) هو عدد أبعاد الإخراج و \(N\) هو عدد العينات. تُحسّن طريقة Barnes-Hut من الطريقة الدقيقة حيث يكون تعقيد t-SNE هو \(O[d N^2]\)، ولكن لديها العديد من الاختلافات الملحوظة الأخرى:

• يعمل تطبيق Barnes-Hut فقط عندما تكون الأبعاد المستهدفة 3 أو أقل. الحالة ثنائية الأبعاد نموذجية عند بناء التصورات.

• يعمل Barnes-Hut فقط مع بيانات إدخال كثيفة. يمكن تضمين مصفوفات البيانات المتفرقة فقط بالطريقة الدقيقة أو يمكن تقريبها بإسقاط كثيف منخفض الرتبة على سبيل المثال باستخدام PCA

• Barnes-Hut هو تقريب للطريقة الدقيقة. يتم تحديد التقريب بمعامل الزاوية، لذلك لا يتم استخدام معامل الزاوية عند method="exact"

• Barnes-Hut قابل للتحجيم بشكل ملحوظ. يمكن استخدام Barnes-Hut لتضمين مئات الآلاف من نقاط البيانات بينما يمكن للطريقة الدقيقة التعامل مع آلاف العينات قبل أن تصبح مستعصية على الحل حسابيًا

لغرض التصور (وهي الحالة الرئيسية لاستخدام t-SNE)، يوصى بشدة باستخدام طريقة Barnes-Hut. طريقة t-SNE الدقيقة مفيدة للتحقق من الخصائص النظرية للتضمين ربما في فضاء ذي أبعاد أعلى ولكنها تقتصر على مجموعات البيانات الصغيرة نظرًا لقيود الحساب.

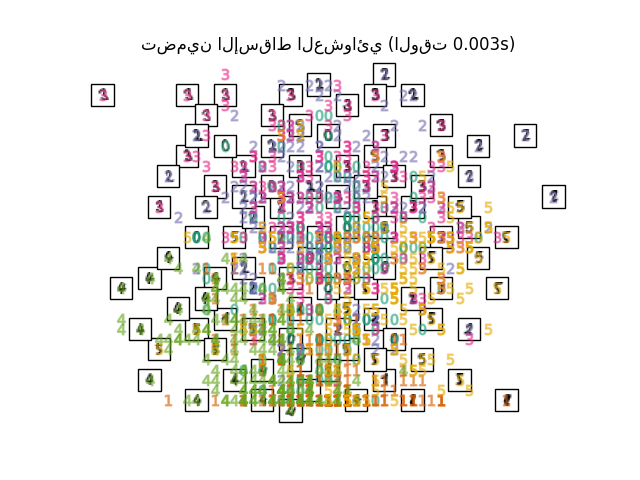
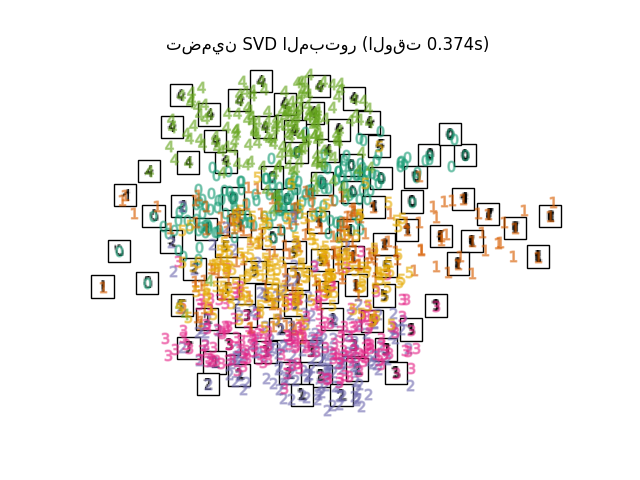
لاحظ أيضًا أن تسميات الأرقام تتطابق تقريبًا مع التجميع الطبيعي الذي وجده t-SNE بينما ينتج عن الإسقاط الخطي ثنائي الأبعاد لنموذج PCA تمثيلًا تتداخل فيه مناطق التسميات إلى حد كبير. هذا دليل قوي على أنه يمكن فصل هذه البيانات جيدًا بواسطة طرق غير خطية تركز على البنية المحلية (على سبيل المثال SVM مع نواة Gaussian RBF). ومع ذلك، فإن الفشل في تصور مجموعات متجانسة التسميات مفصولة جيدًا باستخدام t-SNE في 2D لا يعني بالضرورة أنه لا يمكن تصنيف البيانات بشكل صحيح بواسطة نموذج خاضع للإشراف. قد يكون الأمر أن البعدين ليسا مرتفعين بما يكفي لتمثيل البنية الداخلية للبيانات بدقة.

المراجع

• "Visualizing High-Dimensional Data Using t-SNE" van der Maaten, L.J.P.; Hinton, G. Journal of Machine Learning Research (2008)

• "t-Distributed Stochastic Neighbor Embedding" van der Maaten, L.J.P.

• "Accelerating t-SNE using Tree-Based Algorithms" van der Maaten, L.J.P.; Journal of Machine Learning Research 15(Oct):3221-3245, 2014.

• "Automated optimized parameters for T-distributed stochastic neighbor embedding improve visualization and analysis of large datasets" Belkina, A.C., Ciccolella, C.O., Anno, R., Halpert, R., Spidlen, J., Snyder-Cappione, J.E., Nature Communications 10, 5415 (2019).

2.2.10. نصائح حول الاستخدام العملي

• تأكد من استخدام نفس المقياس على جميع الميزات. نظرًا لأن أساليب تعلم المشعبات تعتمد على بحث أقرب جار، فقد تؤدي الخوارزمية أداءً ضعيفًا بخلاف ذلك. انظر StandardScaler للحصول على طرق ملائمة لتحجيم البيانات غير المتجانسة.

• يمكن استخدام خطأ إعادة البناء الذي يحسبه كل روتين لاختيار بُعد الإخراج الأمثل. بالنسبة لمشعب ذي أبعاد \(d\) مضمن في فضاء معلمات ذي أبعاد \(D\)، سينخفض ​​خطأ إعادة البناء مع زيادة n_components حتى n_components == d.

• لاحظ أن البيانات المزعجة يمكن أن "تقصر" المشعب، وتعمل بشكل أساسي كجسر بين أجزاء المشعب التي ستكون بخلاف ذلك منفصلة جيدًا. تعلم المشعبات على البيانات المزعجة و/أو غير المكتملة هو مجال بحث نشط.

• يمكن أن تؤدي تكوينات إدخال معينة إلى مصفوفات وزن فردية، على سبيل المثال عندما تكون أكثر من نقطتين في مجموعة البيانات متطابقتين، أو عندما يتم تقسيم البيانات إلى مجموعات منفصلة. في هذه الحالة، سيفشل solver='arpack' في العثور على مساحة فارغة. أسهل طريقة لمعالجة هذا هي استخدام solver='dense' الذي سيعمل على مصفوفة فردية، على الرغم من أنه قد يكون بطيئًا جدًا اعتمادًا على عدد نقاط الإدخال. بدلاً من ذلك، يمكن للمرء محاولة فهم مصدر التفرد: إذا كان ذلك بسبب مجموعات منفصلة، فقد تساعد زيادة n_neighbors. إذا كان ذلك بسبب نقاط متطابقة في مجموعة البيانات، فقد تساعد إزالة هذه النقاط.

شاهد أيضا

تضمين الأشجار العشوائية تمامًا يمكن أن يكون مفيدًا أيضًا لاستخلاص تمثيلات غير خطية لفضاء الميزات، كما أنه لا يؤدي اختزال الأبعاد.

================= ترجمة باستخدام Command-pluse ====================================================================

ابحث عن الضروريات الأساسية

الضروريات الأساسية البسيطة

انسَ همومك ومشاكلك

أعني الضروريات الأساسية

وصفات الأم الطبيعة

التي تجلب الضروريات الأساسية للحياة

-- أغنية بالو [كتاب الأدغال]

تعلم المانيفولد هو نهج لخفض الأبعاد غير الخطي. تستند الخوارزميات لهذه المهمة على فكرة أن الأبعاد للعديد من مجموعات البيانات تكون عالية بشكل مصطنع فقط.

2.2.11. مقدمة

يمكن أن تكون مجموعات البيانات عالية الأبعاد صعبة للغاية في التصور. في حين يمكن رسم البيانات في بعدين أو ثلاثة أبعاد لإظهار البنية الكامنة للبيانات، تكون الرسوم البيانية عالية الأبعاد أقل حدسية. للمساعدة في تصور بنية مجموعة البيانات، يجب تقليل البعد بطريقة ما.

أبسط طريقة لتحقيق هذا الخفض للأبعاد هي عن طريق أخذ إسقاط عشوائي للبيانات. على الرغم من أن هذا يسمح ببعض درجة من تصور بنية البيانات، فإن عشوائية الاختيار تترك الكثير مما هو مرغوب فيه. في الإسقاط العشوائي، من المحتمل أن يتم فقدان البنية الأكثر إثارة للاهتمام داخل البيانات.

لمعالجة هذا القلق، تم تصميم عدد من الأطر الخطية وغير الخطية لخفض الأبعاد، مثل تحليل المكونات الرئيسية (PCA)، وتحليل المكونات المستقلة، وتحليل التمييز الخطي، وغيرها. تحدد هذه الخوارزميات قواعد محددة لاختيار إسقاط خطي "مثير للاهتمام" للبيانات. يمكن أن تكون هذه الطرق قوية، ولكنها غالبًا ما تفوت بنية غير خطية مهمة في البيانات.

يمكن اعتبار تعلم المانيفولد على أنه محاولة لتعميم الأطر الخطية مثل PCA لتصبح حساسة للبنية غير الخطية في البيانات. على الرغم من وجود متغيرات خاضعة للإشراف، فإن مشكلة تعلم المانيفولد النموذجية غير خاضعة للإشراف: فهي تتعلم البنية عالية الأبعاد للبيانات من البيانات نفسها، دون استخدام التصنيفات المحددة مسبقًا.

أمثلة

• راجع تعلم متعدد الشعب على الأرقام المكتوبة بخط اليد: التضمين الخطي المحلي، Isomap... لمثال على خفض الأبعاد على الأرقام المكتوبة بخط اليد.

• راجع مقارنة طرق تعلم متعدد الشعب لمثال على خفض الأبعاد على مجموعة بيانات "S-curve" لعبة.

• راجع هيكلة سوق الأسهم المرئية لمثال على استخدام تعلم المانيفولد لرسم خريطة لهيكل سوق الأسهم بناءً على أسعار الأسهم التاريخية.

تتوفر عمليات تنفيذ تعلم المانيفولد في scikit-learn ملخصة أدناه

2.2.12. Isomap

أحد أقدم الأساليب لتعلم المانيفولد هو خوارزمية Isomap، اختصارًا لـ Isometric Mapping. يمكن اعتبار Isomap كتوسيع لتقليص الأبعاد متعدد الأبعاد (MDS) أو Kernel PCA. يبحث Isomap عن تضمين أقل أبعادًا يحافظ على المسافات الجيوديسية بين جميع النقاط. يمكن إجراء Isomap باستخدام الكائن Isomap.

التعقيد

تتكون خوارزمية Isomap من ثلاث مراحل:

1. بحث الجار الأقرب. يستخدم Isomap BallTree للبحث عن الجيران بكفاءة. تبلغ التكلفة تقريبًا \(O[D \log(k) N \log(N)]\)، لـ \(k\) الجيران الأقرب لـ \(N\) نقاط في \(D\) أبعاد.

2. بحث الرسم البياني لأقصر مسار. أكثر الخوارزميات المعروفة كفاءة لهذا هي خوارزمية ديكسترا، والتي تبلغ تقريبًا \(O[N^2(k + \log(N))]\)، أو خوارزمية فلويد-وارشال، والتي هي \(O[N^3]\). يمكن للمستخدم تحديد الخوارزمية باستخدام الكلمة الرئيسية path_method من Isomap. إذا لم يتم تحديدها، يحاول الكود اختيار أفضل خوارزمية للبيانات المدخلة.

3. التحليل الجزئي للقيمة الذاتية. يتم ترميز التضمين في المكونات الذاتية المقابلة لـ \(d\) أكبر قيم ذاتية لـ \(N \times N\) نواة Isomap. بالنسبة للحل الكثيف، تبلغ التكلفة تقريبًا \(O[d N^2]\). يمكن تحسين هذه التكلفة غالبًا باستخدام محول ARPACK. يمكن للمستخدم تحديد المحلل الذاتي باستخدام الكلمة الرئيسية eigen_solver من Isomap. إذا لم يتم تحديدها، يحاول الكود اختيار أفضل خوارزمية للبيانات المدخلة.

التعقيد الإجمالي لـ Isomap هو \(O[D \log(k) N \log(N)] + O[N^2(k + \log(N))] + O[d N^2]\).

• \(N\) : عدد نقاط التدريب

• \(D\) : البعد المدخلة

• \(k\) : عدد الجيران الأقرب

• \(d\) : البعد الإخراج

المراجع

• "إطار عمل هندسي عالمي لخفض الأبعاد غير الخطي" Tenenbaum, J.B.; De Silva, V.; & Langford, J.C. Science 290 (5500)

2.2.13. التضمين الخطي المحلي

يسعى التضمين الخطي المحلي (LLE) إلى تضمين أقل أبعادًا للبيانات التي تحافظ على المسافات داخل الأحياء المحلية. يمكن اعتباره سلسلة من تحليلات المكونات الرئيسية المحلية التي يتم مقارنتها عالميًا لإيجاد أفضل تضمين غير خطي.

يمكن إجراء التضمين الخطي المحلي باستخدام الدالة locally_linear_embedding أو نظيرها الموجه نحو الكائنات LocallyLinearEmbedding.

التعقيد

تتكون خوارزمية LLE القياسية من ثلاث مراحل:

1. بحث الجار الأقرب. راجع المناقشة تحت Isomap أعلاه.

2. بناء مصفوفة الأوزان. \(O[D N k^3]\). يتضمن بناء مصفوفة الأوزان الخطية المحلية حل معادلة خطية \(k \times k\) لكل من الأحياء المحلية \(N\).

3. التحليل الجزئي للقيمة الذاتية. راجع المناقشة تحت Isomap أعلاه.

التعقيد الإجمالي لـ LLE القياسي هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).

• \(N\) : عدد نقاط التدريب

• \(D\) : البعد المدخلة

• \(k\) : عدد الجيران الأقرب

• \(d\) : البعد الإخراج

المراجع

• "خفض الأبعاد غير الخطي بالتضمين الخطي المحلي" Roweis, S. & Saul, L. Science 290:2323 (2000)

2.2.14. التضمين الخطي المحلي المعدل

أحد المشكلات المعروفة جيدًا مع LLE هي مشكلة التنظيم. عندما يكون عدد الجيران أكبر من عدد الأبعاد المدخلة، تكون المصفوفة التي تحدد كل حي محلي ذات رتبة ناقصة. لمعالجة هذا، يطبق LLE القياسي معامل تنظيم عشوائي \(r\)، والذي يتم اختياره نسبيًا إلى أثر مصفوفة الأوزان المحلية. على الرغم من أنه يمكن إظهار رسميًا أنه مع \(r \to 0\)، فإن الحل يتقارب مع التضمين المطلوب، لا يوجد ضمان للعثور على الحل الأمثل لـ \(r > 0\). تظهر هذه المشكلة في التضمينات التي تشوه البنية الأساسية للمانيفولد.

أحد الطرق لمعالجة مشكلة التنظيم هي استخدام ناقلات أوزان متعددة في كل حي. هذه هي جوهر التضمين الخطي المحلي المعدل (MLLE). يمكن إجراء MLLE باستخدام الدالة locally_linear_embedding أو نظيرها الموجه نحو الكائنات LocallyLinearEmbedding، مع الكلمة الرئيسية method = 'modified'. يتطلب n_neighbors > n_components.

التعقيد

تتكون خوارزمية MLLE من ثلاث مراحل:

1. بحث الجار الأقرب. نفس LLE القياسي

2. بناء مصفوفة الأوزان. تقريبًا \(O[D N k^3] + O[N (k-D) k^2]\). المصطلح الأول مكافئ تمامًا لذلك الموجود في LLE القياسي. المصطلح الثاني يتعلق ببناء مصفوفة الأوزان من أوزان متعددة. في الممارسة العملية، تكون التكلفة المضافة لبناء مصفوفة أوزان MLLE صغيرة نسبيًا مقارنة بتكلفة المراحل 1 و 3.

3. التحليل الجزئي للقيمة الذاتية. نفس LLE القياسي

التعقيد الإجمالي لـ MLLE هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N (k-D) k^2] + O[d N^2]\).

• \(N\) : عدد نقاط التدريب

• \(D\) : البعد المدخلة

• \(k\) : عدد الجيران الأقرب

• \(d\) : البعد الإخراج

المراجع

• "MLLE: التضمين الخطي المحلي المعدل باستخدام أوزان متعددة" Zhang, Z. & Wang, J.

2.2.15. رسم خرائط القيمة الذاتية للهيسية

رسم خرائط القيمة الذاتية للهيسية (المعروف أيضًا باسم LLE القائم على الهيسية: HLLE) هو طريقة أخرى لحل مشكلة التنظيم لـ LLE. تدور حول شكل رباعي الهيسية في كل حي والذي يتم استخدامه لاسترداد البنية الخطية المحلية. على الرغم من أن التطبيقات الأخرى تشير إلى سوء قياسها مع حجم البيانات، فإن sklearn ينفذ بعض التحسينات الخوارزمية التي تجعل تكلفتها قابلة للمقارنة مع تلك الخاصة بمتغيرات LLE الأخرى للبعد الإخراج الصغير. يمكن إجراء HLLE باستخدام الدالة locally_linear_embedding أو نظيرها الموجه نحو الكائنات LocallyLinearEmbedding، مع الكلمة الرئيسية method = 'hessian'. يتطلب n_neighbors > n_components * (n_components + 3) / 2.

التعقيد

تتكون خوارزمية HLLE من ثلاث مراحل:

1. بحث الجار الأقرب. نفس LLE القياسي

2. بناء مصفوفة الأوزان. تقريبًا \(O[D N k^3] + O[N d^6]\). يعكس المصطلح الأول تكلفة مماثلة لتلك الموجودة في LLE القياسي. يأتي المصطلح الثاني من تحليل QR لمقدر الهيسية المحلية.

3. التحليل الجزئي للقيمة الذاتية. نفس LLE القياسي.

التعقيد الإجمالي لـ HLLE القياسي هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N d^6] + O[d N^2]\).

• \(N\) : عدد نقاط التدريب

• \(D\) : البعد المدخلة

• \(k\) : عدد الجيران الأقرب

• \(d\) : البعد الإخراج

المراجع

• "خرائط القيمة الذاتية للهيسية: تقنيات التضمين الخطي المحلية للبيانات عالية الأبعاد" Donoho, D. & Grimes, C. Proc Natl Acad Sci USA. 100:5591 (2003)

2.2.16. التضمين الطيفي

التضمين الطيفي هو نهج لحساب تضمين غير خطي. ينفذ scikit-learn خرائط لابلاسيان، والتي تجد تمثيلًا منخفض الأبعاد للبيانات باستخدام تحليل طيفي لمصفوفة لابلاسيان الرسم البياني. يمكن اعتبار الرسم البياني المولد على أنه تقريب منفصل للمانيفولد منخفض الأبعاد في الفضاء عالي الأبعاد. يضمن تقليل دالة التكلفة بناءً على الرسم البياني أن النقاط القريبة من بعضها البعض على المانيفولد يتم رسمها بالقرب من بعضها البعض في الفضاء منخفض الأبعاد، مما يحافظ على المسافات المحلية. يمكن إجراء التضمين الطيفي باستخدام الدالة spectral_embedding أو نظيرها الموجه نحو الكائنات SpectralEmbedding.

التعقيد

تتكون خوارزمية التضمين الطيفي (خرائط لابلاسيان) من ثلاث مراحل:

1. بناء الرسم البياني المرجح. تحويل بيانات الإدخال الخام إلى تمثيل الرسم البياني باستخدام مصفوفة تمثيل التقارب (المجاورات).

2. بناء لابلاسيان الرسم البياني. يتم بناء لابلاسيان غير المعياري كـ \(L = D - A\) ولابلاسيان المعياري كـ \(L = D^{-\frac{1}{2}} (D - A) D^{-\frac{1}{2}}\).

3. التحليل الجزئي للقيمة الذاتية. يتم إجراء التحليل الذاتي للقيمة على لابلاسيان الرسم البياني.

التعقيد الإجمالي للتضمين الطيفي هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).

• \(N\) : عدد نقاط التدريب

• \(D\) : البعد المدخلة

• \(k\) : عدد الجيران الأقرب

• \(d\) : البعد الإخراج

المراجع

• "خرائط لابلاسيان لخفض الأبعاد وتمثيل البيانات" M. Belkin, P. Niyogi, Neural Computation, June 2003; 15 (6):1373-1396

2.2.17. محاذاة الفضاء المماس المحلي

على الرغم من أنها ليست متغيرًا تقنيًا لـ LLE، إلا أن محاذاة الفضاء المماس المحلي (LTSA) تشبه خوارزميًا بما يكفي لـ LLE لوضعها في هذه الفئة. بدلاً من التركيز على الحفاظ على المسافات داخل الحي كما في LLE، تسعى LTSA لتوصيف الهندسة المحلية في كل حي من خلال مساحته المماسة، وتؤدي تحسينًا عالميًا لمحاذاة هذه المساحات المماسة المحلية لتعلم التضمين. يمكن إجراء LTSA باستخدام الدالة locally_linear_embedding أو نظيرها الموجه نحو الكائنات LocallyLinearEmbedding، مع الكلمة الرئيسية method = 'ltsa'.

التعقيد

تتكون خوارزمية LTSA من ثلاث مراحل:

1. بحث الجار الأقرب. نفس LLE القياسي

2. بناء مصفوفة الأوزان. تقريبًا \(O[D N k^3] + O[k^2 d]\). يعكس المصطلح الأول تكلفة مماثلة لتلك الموجودة في LLE القياسي.

3. التحليل الجزئي للقيمة الذاتية. نفس LLE القياسي

التعقيد الإجمالي لـ LTSA القياسي هو \(O[D \log(k) N \log(N)] + O[D N k^3] + O[k^2 d] + O[d N^2]\).

• \(N\) : عدد نقاط التدريب

• \(D\) : البعد المدخلة

• \(k\) : عدد الجيران الأقرب

• \(d\) : البعد الإخراج

المراجع

• :arxiv:`"المنحنيات الرئيسية ومحاذاة الفضاء المماس لخفض الأبعاد غير الخطي" <cs/0212008>`_ Zhang, Z. & Zha, H. Journal of Shanghai Univ. 8:406 (2004)

2.2.18. القياس متعدد الأبعاد (MDS)

القياس متعدد الأبعاد (MDS) يسعى إلى تمثيل منخفض الأبعاد للبيانات التي تحترم المسافات جيدًا في الفضاء عالي الأبعاد الأصلي.

بشكل عام، MDS هي تقنية مستخدمة لتحليل بيانات التشابه أو الاختلاف. تحاول نمذجة بيانات التشابه أو الاختلاف كمسافات في مساحات هندسية. يمكن أن تكون البيانات تقييمات للتشابه بين الكائنات، أو ترددات التفاعل للجزيئات، أو مؤشرات التجارة بين البلدان.

يوجد نوعان من خوارزمية MDS: المترية وغير المترية. في scikit-learn، تنفذ الفئة MDS كلا النوعين. في MDS المترية، تنشأ مصفوفة التشابه المدخلة من مقياس (وبالتالي تحترم عدم المساواة المثلثية)، يتم تعيين المسافات بين نقطتين على أنها قريبة قدر الإمكان من بيانات التشابه أو الاختلاف. في الإصدار غير المتري، ستحاول الخوارزميات الحفاظ على ترتيب المسافات، وبالتالي تسعى لإيجاد علاقة أحادية الاتجاه بين المسافات في الفضاء المضمن والتشابهات/الاختلافات.

دع \(S\) تكون مصفوفة التشابه، و \(X\) إحداثيات \(n\) نقاط الإدخال. الفوارق \(\hat{d}_{ij}\) هي تحويل التشابهات المختارة بطرق مثالية. يتم تعريف الهدف، المسمى الإجهاد، بعد ذلك بواسطة \(\sum_{i < j} d_{ij}(X) - \hat{d}_{ij}(X)\)

MDS المترية

أبسط نموذج MDS متري، يسمى MDS المطلق، يتم تعريف الفوارق بواسطة \(\hat{d}_{ij} = S_{ij}\). مع MDS المطلق، يجب أن تقابل القيمة \(S_{ij}\) بالضبط المسافة بين النقطة \(i\) و \(j\) في نقطة التضمين.

غالبًا ما يتم تعيين الفوارق إلى \(\hat{d}_{ij} = b S_{ij}\).

MDS غير المترية

يركز MDS غير المتري على ترتيب البيانات. إذا \(S_{ij} > S_{jk}\)، فيجب أن يفرض التضمين \(d_{ij} < d_{jk}\). لهذا السبب، نناقشه من حيث الاختلافات (\(\delta_{ij}\)) بدلاً من التشابهات (\(S_{ij}\)). لاحظ أن الاختلافات يمكن الحصول عليها بسهولة من التشابهات من خلال تحويل بسيط، على سبيل المثال \(\delta_{ij}=c_1-c_2 S_{ij}\) لبعض الثوابت \(c_1, c_2\). خوارزمية بسيطة لفرض ترتيب صحيح هي استخدام تراجع أحادي مع \(d_{ij}\) على \(\delta_{ij}\)، مما يؤدي إلى فوارق \(\hat{d}_{ij}\) بنفس ترتيب \(\delta_{ij}\).

حل بديهي لهذه المشكلة هو تعيين جميع النقاط على الأصل. لتجنب ذلك، يتم تطبيع الفوارق \(\hat{d}_{ij}\). لاحظ أنه نظرًا لأننا نهتم فقط بالترتيب النسبي، يجب أن يكون هدفنا غير حساس للترجمة والتوسيع البسيط، ومع ذلك فإن الإجهاد المستخدم في MDS المتري حساس للتوسيع. لمعالجة هذا، قد يستخدم MDS غير المتري إجهادًا معياريًا، يُعرف باسم Stress-1، ويتم تعريفه كـ

\[\sqrt{\frac{\sum_{i < j} (d_{ij} - \hat{d}_{ij})^2}{\sum_{i < j} d_{ij}^2}}.\]

يمكن تمكين استخدام إجهاد Stress-1 المعياري من خلال تعيين normalized_stress=True، ومع ذلك فهو متوافق فقط مع مشكلة MDS غير المترية وسيتم تجاهله في الحالة المترية.

المراجع

• "القياس متعدد الأبعاد الحديث - النظرية والتطبيقات" Borg, I.; Groenen P. Springer Series in Statistics (1997)

• "القياس متعدد الأبعاد غير المتري: طريقة رقمية" Kruskal, J. Psychometrika, 29 (1964)

• "القياس متعدد الأبعاد عن طريق تحسين ملاءمة الفرضية غير المترية" Kruskal, J. Psychometrika, 29, (1964)

2.2.19. التضمين العشوائي للجيران (t-SNE)

يحول t-SNE (TSNE) التقاربات لنقاط البيانات إلى احتمالات. يتم تمثيل التقاربات في الفضاء الأصلي بواسطة احتمالات مشتركة غاوسية والتقاربات في الفضاء المضمن يتم تمثيلها بواسطة توزيعات طالب. يسمح هذا لـ t-SNE بأن يكون حساسًا للهيكل المحلي ولديه بعض المزايا الأخرى على التقنيات الموجودة:

• الكشف عن البنية على العديد من المقاييس على خريطة واحدة

• الكشف عن البيانات الموجودة في العديد من المانيفولدات أو المجموعات المختلفة

• تقليل الميل إلى تجميع النقاط معًا في الوسط

في حين أن Isomap وLLE والمتغيرات مناسبة بشكل أفضل لفتح مانيفولد مستمر منخفض الأبعاد، سيركز t-SNE على البنية المحلية للبيانات وسيميل إلى استخراج مجموعات محلية من العينات المدمجة كما هو موضح في مثال S-curve. قد تكون هذه القدرة على تجميع العينات بناءً على البنية المحلية مفيدة في فك تشابك مجموعة بيانات تتكون من العديد من المانيفولدات في نفس الوقت كما هو الحال في مجموعة بيانات الأرقام.

سيتم تقليل تباعد كولباك-لايبلر (KL) للاحتمالات المشتركة في الفضاء الأصلي والفضاء المضمن بواسطة التدرج الهابط. لاحظ أن تباعد KL ليس محدبًا، أي أن عمليات إعادة التشغيل المتعددة مع التهيئات الأولية المختلفة ستنتهي في الحد الأدنى المحلي لتباعد KL. وبالتالي، من المفيد في بعض الأحيان تجربة بذور مختلفة واختيار التضمين مع أقل تباعد KL.

العيب في استخدام t-SNE هو تقريبًا:

• t-SNE مكلف من الناحية الحسابية، ويمكن أن يستغرق عدة ساعات على مجموعات بيانات المليون عينة حيث تنتهي PCA في ثوانٍ أو دقائق

• تقتصر طريقة Barnes-Hut t-SNE على تضمينات ثنائية أو ثلاثية الأبعاد.

• الخوارزمية عشوائية ويمكن أن تؤدي عمليات إعادة التشغيل المتعددة مع البذور المختلفة إلى تضمينات مختلفة. ومع ذلك، من المشروع تمامًا اختيار التضمين مع أقل خطأ.

• لا يتم الحفاظ على البنية العالمية بشكل صريح. يتم تخفيف هذه المشكلة عن طريق

تهيئة النقاط باستخدام PCA (باستخدام init='pca').

تحسين t-SNE

الغرض الرئيسي من t-SNE هو تصور البيانات عالية الأبعاد. وبالتالي، يعمل بشكل أفضل عندما يتم تضمين البيانات على بعدين أو ثلاثة أبعاد.

يمكن أن يكون تحسين تباعد KL معقدًا بعض الشيء في بعض الأحيان. هناك خمسة معلمات تتحكم في تحسين t-SNE وبالتالي ربما جودة التضمين الناتج:

• الغموض

• عامل المبالغة المبكرة

• معدل التعلم

• عدد التكرارات القصوى

• الزاوية (غير مستخدمة في الطريقة الدقيقة)

يتم تعريف الغموض على أنه \(k=2^{(S)}\) حيث \(S\) هي إنتروبيا شانون لتوزيع الاحتمال الشرطي. الغموض لمكعب ذو \(k\) جوانب هو \(k\)، لذا فإن \(k\) هو عدد الجيران الأقرب الذي ينظر إليه t-SNE عند توليد الاحتمالات الشرطية. تؤدي الغموض الأكبر إلى مزيد من الجيران الأقرب وأقل حساسية للبنية الصغيرة. على العكس من ذلك، يؤدي الغموض المنخفض إلى النظر في عدد أقل من الجيران، وبالتالي تجاهل المزيد من المعلومات العالمية لصالح

الحي المحلي. مع زيادة أحجام مجموعات البيانات، ستكون هناك حاجة إلى مزيد من النقاط للحصول على عينة جيدة من الحي المحلي، وبالتالي قد تكون هناك حاجة إلى غموض أكبر. وبالمثل، قد تتطلب مجموعات البيانات الأكثر ضوضاءً قيم غموض أكبر لتجاوز الضوضاء الخلفية ورؤية ما يكفي من الجيران المحليين.

عادةً ما يكون عدد التكرارات القصوى مرتفعًا بما يكفي ولا يحتاج

إلى أي ضبط. يتكون التحسين من مرحلتين: مرحلة المبالغة المبكرة والتحسين النهائي. خلال المبالغة المبكرة، سيتم زيادة الاحتمالات المشتركة في الفضاء الأصلي بشكل مصطنع عن طريق الضرب في عامل معين. تؤدي العوامل الأكبر إلى فجوات أكبر بين المجموعات الطبيعية في البيانات. إذا كان العامل مرتفعًا جدًا، فقد يزيد تباعد KL خلال هذه المرحلة. عادةً لا يحتاج إلى ضبطه. معلمة حرجة هي معدل التعلم. إذا كان منخفضًا للغاية، فسيعلق التدرج الهابط في حد أدنى محلي سيء. إذا كان مرتفعًا جدًا، فسيتم زيادة تباعد KL أثناء التحسين. اقترحت حيلة في Belkina et al. (2019) لتعيين معدل التعلم إلى حجم العينة مقسومًا على عامل المبالغة المبكرة. ننفذ هذه الحيلة كحجة learning_rate='auto'. يمكن العثور على المزيد من النصائح في أسئلة وأجوبة لورانس فان دير مايتن (راجع المراجع). المعلمة الأخيرة، الزاوية، هي توازن بين الأداء والدقة. تشير الزوايا الأكبر إلى أنه يمكننا تقريب مناطق أكبر بنقطة واحدة، مما يؤدي إلى تحسين السرعة ولكن نتائج أقل دقة.

"كيفية استخدام t-SNE بشكل فعال" يوفر مناقشة جيدة لآثار المعلمات المختلفة، بالإضافة إلى مخططات تفاعلية لاستكشاف آثار المعلمات المختلفة.

Barnes-Hut t-SNE

طريقة Barnes-Hut t-SNE التي تم تنفيذها هنا تكون عادةً أبطأ من

خوارزميات تعلم المانيفولد الأخرى. يكون التحسين صعبًا وتكون تكلفة حساب التدرج \(O[d N log(N)]\)، حيث \(d\) هو عدد الأبعاد الإخراجية و \(N\) هو عدد العينات. تحسن طريقة Barnes-Hut على الطريقة الدقيقة حيث تكون تعقيد t-SNE هو \(O[d N^2]\)، ولكن لديها بعض الاختلافات الملحوظة الأخرى:

• تعمل طريقة Barnes-Hut فقط عندما يكون البعد المستهدف 3 أو أقل. تكون حالة 2D نموذجية عند بناء التصورات.

• تعمل طريقة Barnes-Hut فقط مع بيانات الإدخال الكثيفة. يمكن تضمين البيانات المتناثرة فقط بالطريقة الدقيقة أو يمكن تقريبها بواسطة إسقاط منخفض الرتبة كثيف على سبيل المثال باستخدام PCA

• طريقة Barnes-Hut هي تقريب للطريقة الدقيقة. يتم معلمة التقريب

بمعلمة الزاوية، وبالتالي يتم تجاهل معلمة الزاوية عند method="exact" * طريقة Barnes-Hut قابلة للتطوير بشكل كبير. يمكن استخدام Barnes-Hut لتضمين مئات الآلاف من نقاط البيانات في حين أن الطريقة الدقيقة يمكنها التعامل مع آلاف العينات قبل أن تصبح غير عملية من الناحية الحسابية

بالنسبة لغرض التصور (الذي هو الاستخدام الرئيسي لـ t-SNE)، يوصى بشدة باستخدام

طريقة Barnes-Hut. الطريقة الدقيقة لـ t-SNE مفيدة للتأكد من الخصائص النظرية للتضمين في مساحة ذات أبعاد أعلى ولكنها مقيدة بمجموعات بيانات صغيرة بسبب القيود الحسابية.

لاحظ أيضًا أن تسميات الأرقام تتطابق تقريبًا مع التجميع الطبيعي الذي وجده

t-SNE في حين أن الإسقاط ثنائي الأبعاد الخطي لنموذج PCA ينتج تمثيلًا حيث تتداخل مناطق التسميات إلى حد كبير. هذا دليل قوي على أنه يمكن فصل هذه البيانات جيدًا بواسطة طرق غير خطية تركز على البنية المحلية (مثل SVM مع RBF غاوسي). ومع ذلك، فإن الفشل في تصور المجموعات المسماة جيدًا والمفصولة في 2D باستخدام t-SNE لا يعني بالضرورة أن البيانات لا يمكن تصنيفها بشكل صحيح بواسطة نموذج خاضع للإشراف. قد يكون الأمر أن بعدين غير كافيين لتمثيل البنية الداخلية للبيانات بدقة.

المراجع

• "تصور البيانات عالية الأبعاد باستخدام t-SNE" van der Maaten, L.J.P.; Hinton, G. Journal of Machine Learning Research (2008)

• "التضمين العشوائي للجيران" van der Maaten, L.J.P.

• "تسريع t-SNE باستخدام خوارزميات شجرية" van der Maaten, L.J.P.; Journal of Machine Learning Research 15(Oct):3221-3245, 2014.

• "معلمات محسنة تلقائيًا لـ t-SNE لتحسين التصور وتحليل مجموعات البيانات الكبيرة" Belkina, A.C., Ciccolella, C.O., Anno, R., Halpert, R., Spidlen, J., Spidlen, J., Nature Communications 10, 5415 (2019).

2.2.20. نصائح للاستخدام العملي

• تأكد من استخدام نفس المقياس على جميع البيانات.

بما أن طرق تعلم المانيفولد تعتمد على بحث الجار الأقرب، فقد يؤدي ذلك إلى أداء سيء. راجع StandardScaler لطرق ملائمة لقياس البيانات غير المتجانسة.

• يمكن استخدام خطأ إعادة البناء الذي يحسبه كل روتين لاختيار

التضمين الأمثل. لمجموعة بيانات ذات أبعاد \(d\) مدمجة في مساحة بارامترية ذات \(D\) أبعاد، سينخفض خطأ إعادة البناء مع زيادة n_components حتى n_components == d.

• لاحظ أن البيانات الضوضائية يمكن أن "تقصر الدائرة" على المانيفولد، في جوهرها تعمل

كجسر بين أجزاء المانيفولد التي ستكون منفصلة بشكل جيد. تعلم المانيفولد على البيانات الضوضائية و/أو غير المكتملة هو مجال نشط للبحث.

• يمكن أن تؤدي تكوينات الإدخال إلى مصفوفات أوزان فردية، على سبيل المثال عندما تكون أكثر من نقطتين في مجموعة البيانات متطابقة، أو عندما تكون البيانات مقسمة إلى مجموعات منفصلة. في هذه الحالة، سيفشل solver='arpack' في العثور على الفضاء الصفري. أسهل طريقة لمعالجة هذا هو

استخدام solver='dense' والذي سيعمل على مصفوفة فردية، على الرغم من أنه قد يكون بطيئًا جدًا اعتمادًا على عدد نقاط الإدخال. بدلاً من ذلك، يمكن للمرء أن يحاول فهم مصدر الفردية: إذا كان بسبب مجموعات منفصلة، فقد يساعد زيادة n_neighbors. إذا كان بسبب نقاط متطابقة، فقد يساعد إزالة هذه النقاط.

شاهد أيضا

تضمين الأشجار العشوائية تمامًا يمكن أن يكون مفيدًا أيضًا في اشتقاق التمثيلات غير الخطية للمساحة المميزة، كما أنه لا يؤدي إلى خفض الأبعاد.