1.15. الانحدار المتساوي التوتر#
تُناسب فئة IsotonicRegression دالة حقيقية غير متناقصة لـ
بيانات أحادية البعد. إنها تحل المشكلة التالية:
\[\min \sum_i w_i (y_i - \hat{y}_i)^2\]
بشرط \(\hat{y}_i \le \hat{y}_j\) كلما كان \(X_i \le X_j\)،
حيث تكون الأوزان \(w_i\) موجبة تمامًا، و X و y
كميات حقيقية عشوائية.
تُغير معلمة increasing القيد إلى
\(\hat{y}_i \ge \hat{y}_j\) كلما كان \(X_i \le X_j\). سيؤدي تعيينها إلى
'auto' إلى اختيار القيد تلقائيًا بناءً على معامل ارتباط رتبة سبيرمان.
تُنتج IsotonicRegression سلسلة من التنبؤات
\(\hat{y}_i\) لبيانات التدريب وهي الأقرب إلى الأهداف
\(y\) من حيث متوسط الخطأ التربيعي. يتم استيفاء هذه التنبؤات
للتنبؤ ببيانات غير مرئية. وبالتالي تُشكِّل تنبؤات IsotonicRegression
دالة خطية متعددة التعريف:
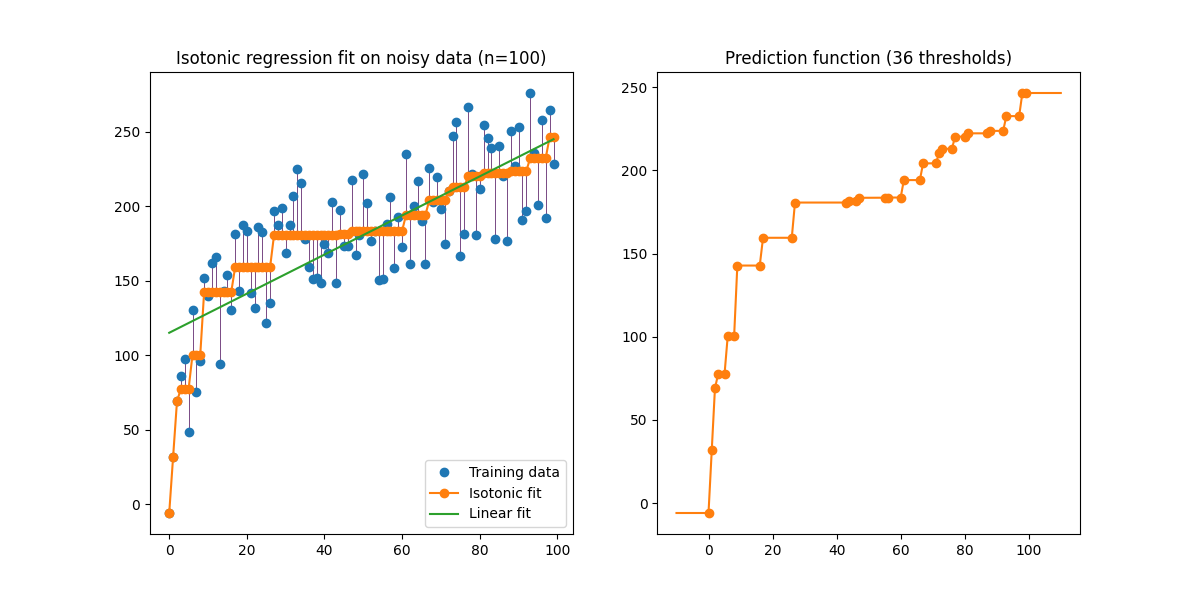
أمثلة
