ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

حدود جونسون-ليندستراوس للانغماس مع الإسقاطات العشوائية#

تنص مبرهنة جونسون-ليندستراوس على أنه يمكن إسقاط أي مجموعة بيانات ذات أبعاد عالية بشكل عشوائي إلى فضاء إقليدي ذي أبعاد أقل مع التحكم في التشوه في المسافات الزوجية.

# المؤلفون: مطوري سكايت-ليرن
# معرف الترخيص: BSD-3-Clause

import sys
from time import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import fetch_20newsgroups_vectorized, load_digits
from sklearn.metrics.pairwise import euclidean_distances
from sklearn.random_projection import (
    SparseRandomProjection,
    johnson_lindenstrauss_min_dim
)

الحدود النظرية#

التشوه الذي يسببه الإسقاط العشوائي 'p' يتم تأكيده من خلال حقيقة أن 'p' تحدد غرس eps مع احتمال جيد كما هو محدد بواسطة:

\[(1 - eps) \|u - v\|^2 < \|p(u) - p(v)\|^2 < (1 + eps) \|u - v\|^2\]

حيث 'u' و 'v' هما أي صفين مأخوذين من مجموعة بيانات ذات شكل (n_samples، n_features) و 'p' هو إسقاط بواسطة مصفوفة غاوسية عشوائية 'N(0, 1)' ذات شكل (n_components، n_features) (أو مصفوفة Achlioptas نادرة).

الحد الأدنى لعدد المكونات لضمان غرس eps هو معطى بواسطة:

\[n\_components \geq 4 log(n\_samples) / (eps^2 / 2 - eps^3 / 3)\]

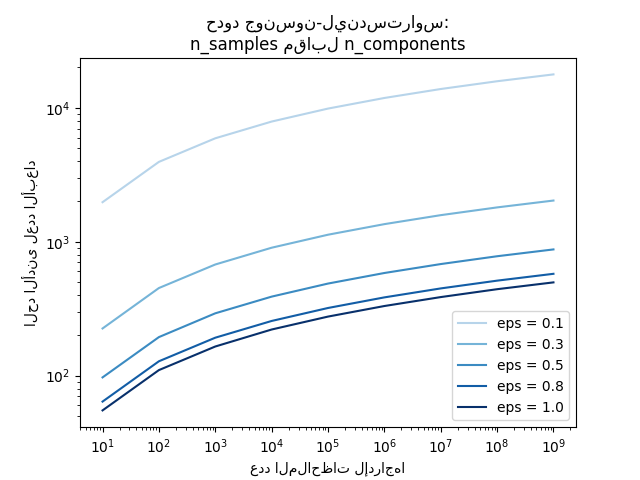
يظهر المخطط الأول أنه مع زيادة عدد العينات "n_samples"، يزداد الحد الأدنى لعدد الأبعاد "n_components" بشكل لوغاريتمي لضمان غرس "eps".

# نطاق التشوهات المسموح بها
eps_range = np.linspace(0.1, 0.99, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(eps_range)))

# نطاق عدد العينات (الملاحظة) لإدراجها
n_samples_range = np.logspace(1, 9, 9)

plt.figure()
for eps, color in zip(eps_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples_range, eps=eps)
    plt.loglog(n_samples_range, min_n_components, color=color)

plt.legend([f"eps = {eps:0.1f}" for eps in eps_range], loc="lower right")
plt.xlabel("عدد الملاحظات لإدراجها")
plt.ylabel("الحد الأدنى لعدد الأبعاد")
plt.title("حدود جونسون-ليندستراوس:\nn_samples مقابل n_components")
plt.show()

حدود جونسون-ليندستراوس: n_samples مقابل n_components

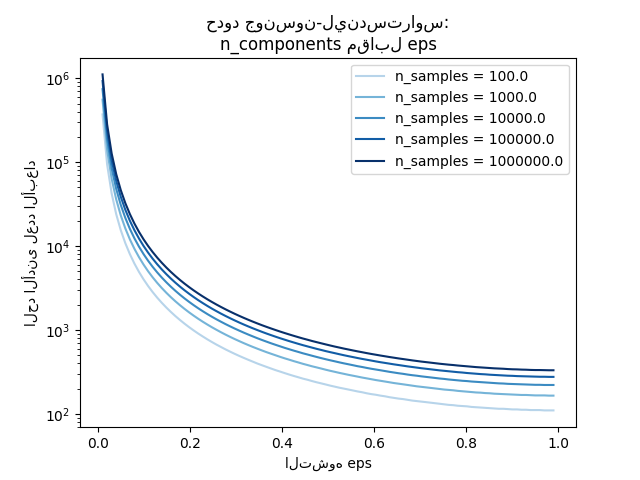
يظهر المخطط الثاني أنه مع زيادة التشوه المسموح به "eps" يسمح بخفض الحد الأدنى بشكل كبير عدد الأبعاد "n_components" لعدد معين من العينات "n_samples"

# نطاق التشوهات المسموح بها
eps_range = np.linspace(0.01, 0.99, 100)

# نطاق عدد العينات (الملاحظة) لإدراجها
n_samples_range = np.logspace(2, 6, 5)
الألوان = plt.cm.Blues(np.linspace(0.3, 1.0, len(n_samples_range)))

plt.figure()
for n_samples, color in zip(n_samples_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples, eps=eps_range)
    plt.semilogy(eps_range, min_n_components, color=color)

plt.legend([f"n_samples = {n}" for n in n_samples_range], loc="upper right")
plt.xlabel("التشوه eps")
plt.ylabel("الحد الأدنى لعدد الأبعاد")
plt.title("حدود جونسون-ليندستراوس:\nn_components مقابل eps")
plt.show()

حدود جونسون-ليندستراوس: n_components مقابل eps

التحقق التجريبي#

نتحقق من الحدود أعلاه على مجموعة بيانات وثائق الأخبار العشرين (ترددات الكلمات TF-IDF) أو على مجموعة بيانات الأرقام:

لمجموعة بيانات الأخبار العشرين، يتم إسقاط بعض الوثائق 300 الميزات في المجموع باستخدام مصفوفة عشوائية نادرة إلى مساحات إقليدية أصغر مع قيم مختلفة للعدد المستهدف من الأبعاد "n_components".
لمجموعة بيانات الأرقام، يتم إسقاط بعض بيانات البكسل بمستوى رمادي 8x8 لصور 300 أرقام مكتوبة بخط اليد بشكل عشوائي إلى مساحات لمختلف عدد أكبر من الأبعاد "n_components".

مجموعة البيانات الافتراضية هي مجموعة بيانات الأخبار العشرين. لتشغيل المثال على مجموعة بيانات الأرقام، قم بتمرير حجة سطر الأوامر "use-digits-dataset" إلى هذا البرنامج النصي.

if "--use-digits-dataset" in sys.argv:
    data = load_digits().data[:300]
else:
    data = fetch_20newsgroups_vectorized().data[:300]

لكل قيمة من "n_components"، نحن نرسم:

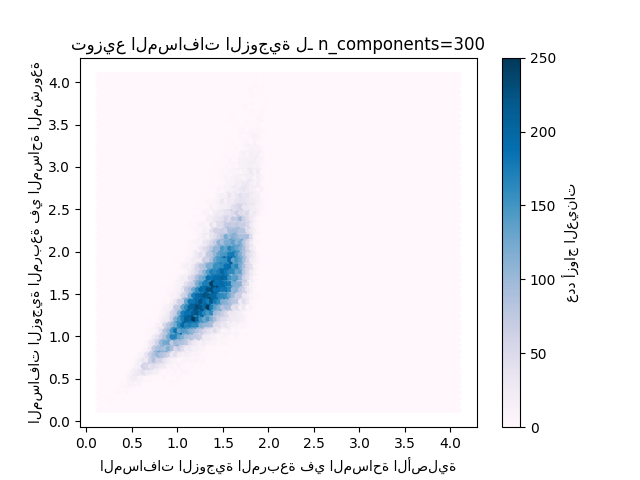
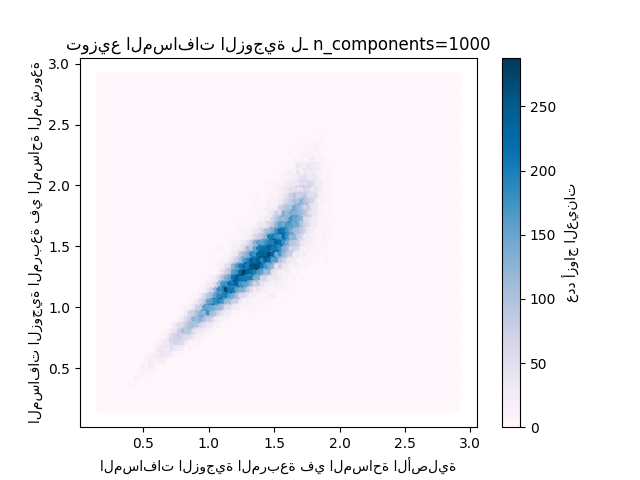
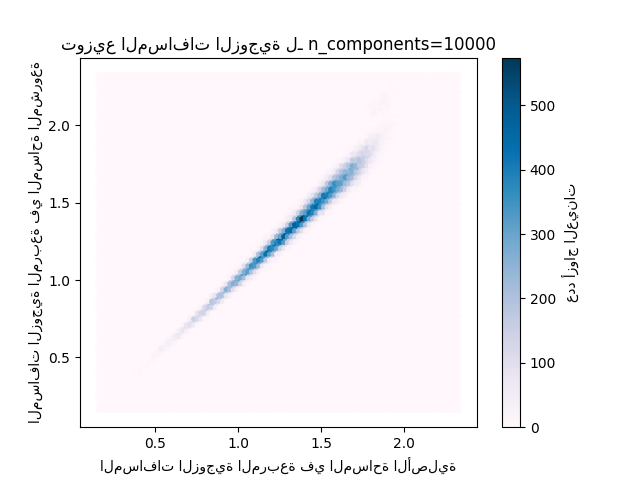
توزيع ثنائي الأبعاد لأزواج العينات مع المسافات الزوجية في المساحات الأصلية والمشروعة كمحور سيني ومحور صادي على التوالي.
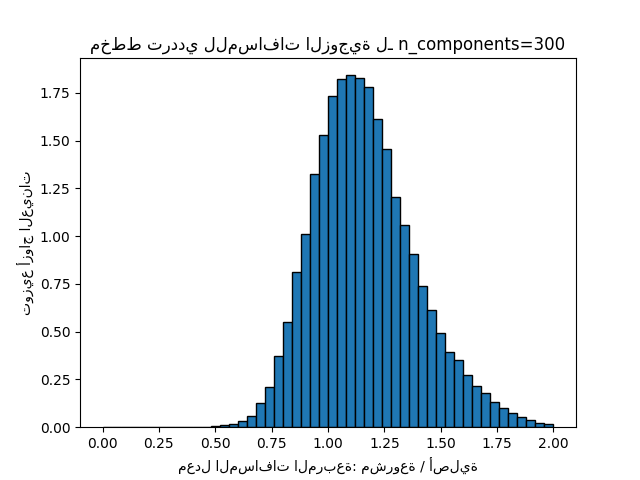
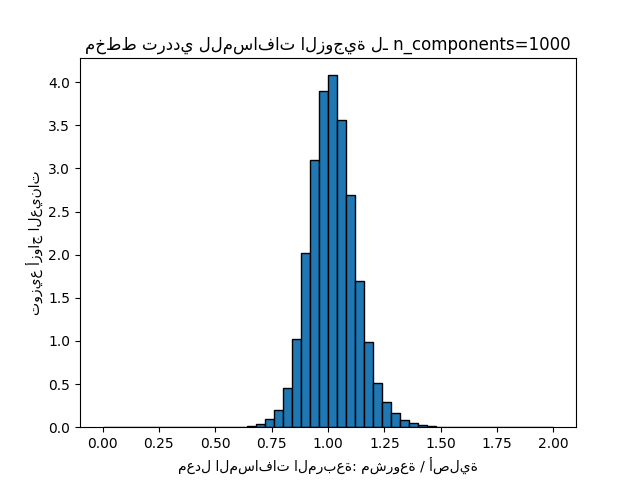
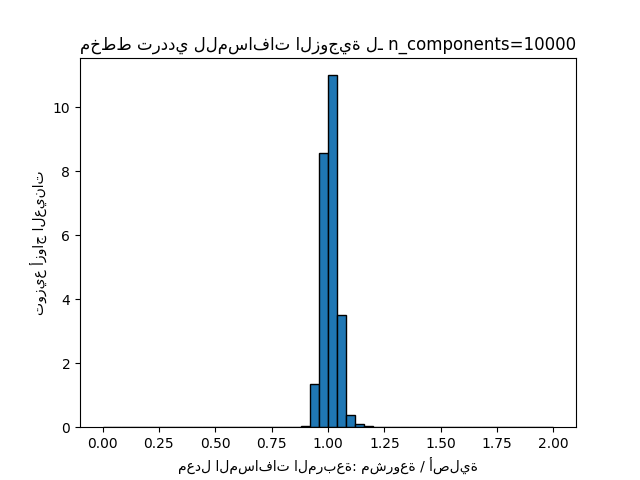
مخطط ترددي أحادي البعد لنسبة تلك المسافات (مشروعة / أصلية).

n_samples, n_features = data.shape
print(
    f"Embedding {n_samples} samples with dim {n_features} using various "
    "random projections"
)

n_components_range = np.array([300, 1_000, 10_000])
dists = euclidean_distances(data, squared=True).ravel()

# حدد فقط أزواج العينات غير المتطابقة
nonzero = dists != 0
dists = dists[nonzero]

for n_components in n_components_range:
    t0 = time()
    rp = SparseRandomProjection(n_components=n_components)
    projected_data = rp.fit_transform(data)
    print(
        f"Projected {n_samples} samples from {n_features} to {n_components} in "
        f"{time() - t0:0.3f}s"
    )
    if hasattr(rp, "components_"):
        n_bytes = rp.components_.data.nbytes
        n_bytes += rp.components_.indices.nbytes
        print(f"Random matrix with size: {n_bytes / 1e6:0.3f} MB")

    projected_dists = euclidean_distances(projected_data, squared=True).ravel()[nonzero]

    plt.figure()
    min_dist = min(projected_dists.min(), dists.min())
    max_dist = max(projected_dists.max(), dists.max())
    plt.hexbin(
        dists,
        projected_dists,
        gridsize=100,
        cmap=plt.cm.PuBu,
        extent=[min_dist, max_dist, min_dist, max_dist],
    )
    plt.xlabel("المسافات الزوجية المربعة في المساحة الأصلية")
    plt.ylabel("المسافات الزوجية المربعة في المساحة المشروعة")
    plt.title("توزيع المسافات الزوجية لـ n_components=%d" % n_components)
    cb = plt.colorbar()
    cb.set_label("عدد أزواج العينات")

    rates = projected_dists / dists
    print(f"Mean distances rate: {np.mean(rates):.2f} ({np.std(rates):.2f})")

    plt.figure()
    plt.hist(rates, bins=50, range=(0.0, 2.0), edgecolor="k", density=True)
    plt.xlabel("معدل المسافات المربعة: مشروعة / أصلية")
    plt.ylabel("توزيع أزواج العينات")
    plt.title("مخطط ترددي للمسافات الزوجية لـ n_components=%d" % n_components)

    # TODO: حساب القيمة المتوقعة لـ eps وإضافتها إلى المخطط السابق
# كخطوط عمودية / منطقة

plt.show()

Embedding 300 samples with dim 130107 using various random projections
Projected 300 samples from 130107 to 300 in 0.387s
Random matrix with size: 1.296 MB
Mean distances rate: 1.17 (0.23)
Projected 300 samples from 130107 to 1000 in 1.248s
Random matrix with size: 4.313 MB
Mean distances rate: 1.02 (0.10)
Projected 300 samples from 130107 to 10000 in 12.371s
Random matrix with size: 43.275 MB
Mean distances rate: 1.01 (0.03)

يمكننا أن نرى أنه بالنسبة للقيم المنخفضة من "n_components" التوزيع واسع مع العديد من الأزواج المشوهة وتوزيع منحرف (بسبب الحد الصلب نسبة الصفر على اليسار حيث تكون المسافات دائمًا إيجابية) في حين أنه بالنسبة للقيم الأكبر من 'n_components' يتم التحكم في التشوه وتحفظ المسافات جيدًا بواسطة الإسقاط العشوائي.

ملاحظات#

وفقًا لمبرهنة JL، سيتطلب إسقاط 300 عينة بدون تشوه كبير سيتطلب ذلك الآلاف من الأبعاد، بغض النظر عن عدد ميزات مجموعة البيانات الأصلية.

وبالتالي، لا معنى لاستخدام الإسقاطات العشوائية على مجموعة بيانات الأرقام التي تحتوي فقط على 64 الميزات في مساحة الإدخال: لا تسمح تقليل الأبعاد في هذه الحالة.

على مجموعة الأخبار العشرين من ناحية أخرى، يمكن تقليل الأبعاد من 56,436 إلى 10,000 مع الحفاظ بشكل معقول على المسافات الزوجية.

Total running time of the script: (0 minutes 18.355 seconds)