ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
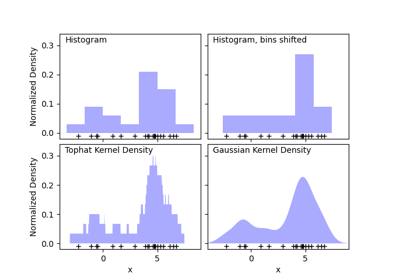
تقدير كثافة النواة#
يوضح هذا المثال كيفية استخدام تقدير كثافة النواة (KDE)، وهي تقنية قوية لتقدير الكثافة غير المعلمية، لتعلم نموذج توليدي لمجموعة بيانات. مع وجود هذا النموذج التوليدي، يمكن رسم عينات جديدة. وتعكس هذه العينات الجديدة النموذج الأساسي للبيانات.

أفضل عرض نطاق ترددي: 3.79269019073225
# المؤلفون: مطوري سكايت-ليرن
# معرف الترخيص: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KernelDensity
# تحميل البيانات
digits = load_digits()
# إسقاط البيانات ذات الأبعاد 64 إلى بعد أقل
pca = PCA(n_components=15, whiten=False)
data = pca.fit_transform(digits.data)
# استخدام البحث الشبكي والتحقق المتقاطع لضبط عرض النطاق الترددي
params = {"bandwidth": np.logspace(-1, 1, 20)}
grid = GridSearchCV(KernelDensity(), params)
grid.fit(data)
print("أفضل عرض نطاق ترددي: {0}".format(grid.best_estimator_.bandwidth))
# استخدام أفضل مقدر لحساب تقدير كثافة النواة
kde = grid.best_estimator_
# أخذ 44 عينة جديدة من البيانات
new_data = kde.sample(44, random_state=0)
new_data = pca.inverse_transform(new_data)
# تحويل البيانات إلى شبكة 4x11
new_data = new_data.reshape((4, 11, -1))
real_data = digits.data[:44].reshape((4, 11, -1))
# رسم الأرقام الحقيقية والأرقام المعاد أخذ عينات منها
fig, ax = plt.subplots(9, 11, subplot_kw=dict(xticks=[], yticks=[]))
for j in range(11):
ax[4, j].set_visible(False)
for i in range(4):
im = ax[i, j].imshow(
real_data[i, j].reshape((8, 8)), cmap=plt.cm.binary, interpolation="nearest"
)
im.set_clim(0, 16)
im = ax[i + 5, j].imshow(
new_data[i, j].reshape((8, 8)), cmap=plt.cm.binary, interpolation="nearest"
)
im.set_clim(0, 16)
ax[0, 5].set_title("اختيار من بيانات الإدخال")
ax[5, 5].set_title('الأرقام "الجديدة" المرسومة من نموذج كثافة النواة')
plt.show()
Total running time of the script: (0 minutes 5.303 seconds)
Related examples
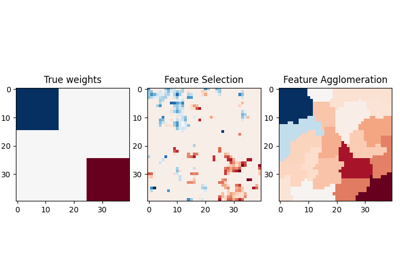
sphx_glr_auto_examples_cluster_plot_feature_agglomeration_vs_univariate_selection.py
# مقارنة بين تجميع الميزات والاختيار أحادي المتغير