ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
هندسة الميزات ذات الصلة بالوقت#
يُقدم هذا الدفتر طرقًا مختلفة للاستفادة من الميزات ذات الصلة بالوقت لمهمة انحدار طلب مشاركة الدراجات التي تعتمد بشكل كبير على دورات العمل (الأيام، والأسابيع، والشهور) ودورات المواسم السنوية.
في هذه العملية، نُقدم كيفية إجراء هندسة الميزات الدورية باستخدام
فئة sklearn.preprocessing.SplineTransformer وخيار
extrapolation="periodic" الخاص بها.
# المؤلفون: مطورو scikit-learn
# مُعرِّف ترخيص SPDX: BSD-3-Clause
استكشاف البيانات على مجموعة بيانات طلب مشاركة الدراجات#
نبدأ بتحميل البيانات من مستودع OpenML.
from sklearn.kernel_approximation import Nystroem
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import FeatureUnion
from sklearn.preprocessing import SplineTransformer
import pandas as pd
from sklearn.preprocessing import FunctionTransformer
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder
from sklearn.linear_model import RidgeCV
import numpy as np
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import cross_validate
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.compose import ColumnTransformer
from sklearn.model_selection import TimeSeriesSplit
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
bike_sharing = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True)
df = bike_sharing.frame
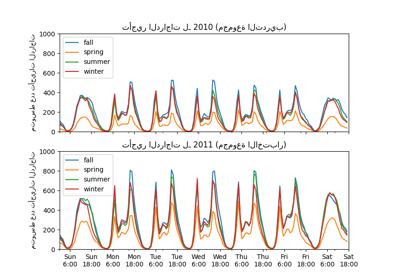
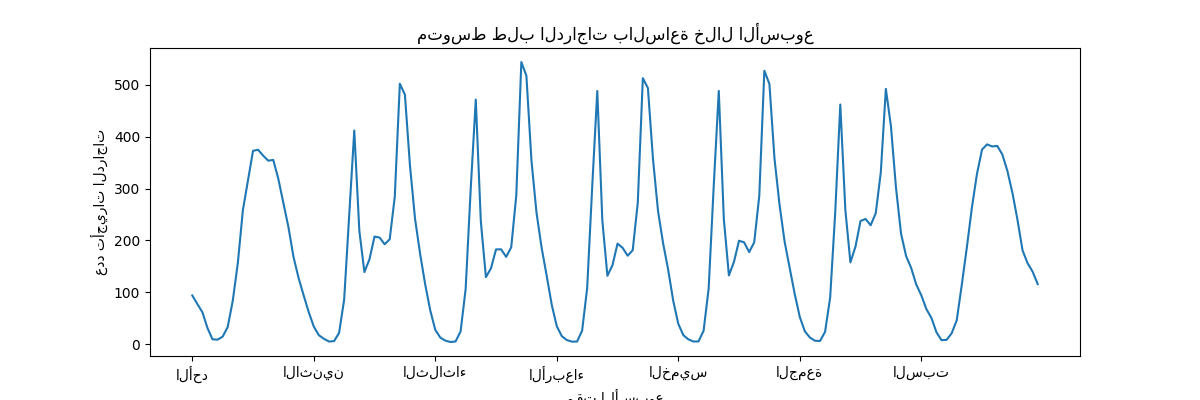
للحصول على فهم سريع للأنماط الدورية للبيانات، دعونا نلقي نظرة على متوسط الطلب في الساعة خلال الأسبوع.
لاحظ أن الأسبوع يبدأ يوم الأحد، خلال عطلة نهاية الأسبوع. يمكننا بوضوح تمييز أنماط التنقل في الصباح والمساء من أيام العمل واستخدام الدراجات الترفيهي في عطلات نهاية الأسبوع مع ذروة طلب أكثر انتشارًا في منتصف الأيام:
fig, ax = plt.subplots(figsize=(12, 4))
average_week_demand = df.groupby(["weekday", "hour"])["count"].mean()
average_week_demand.plot(ax=ax)
_ = ax.set(
title="متوسط طلب الدراجات بالساعة خلال الأسبوع",
xticks=[i * 24 for i in range(7)],
xticklabels=["الأحد", "الاثنين", "الثلاثاء",
"الأربعاء", "الخميس", "الجمعة", "السبت"],
xlabel="وقت الأسبوع",
ylabel="عدد تأجيرات الدراجات",
)
هدف مشكلة التنبؤ هو العدد المطلق لتأجيرات الدراجات على أساس كل ساعة:
df["count"].max()
977
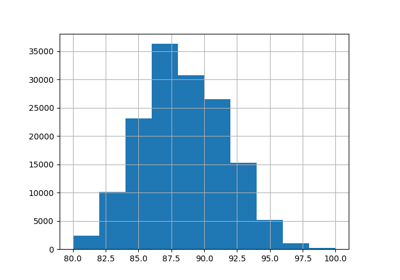
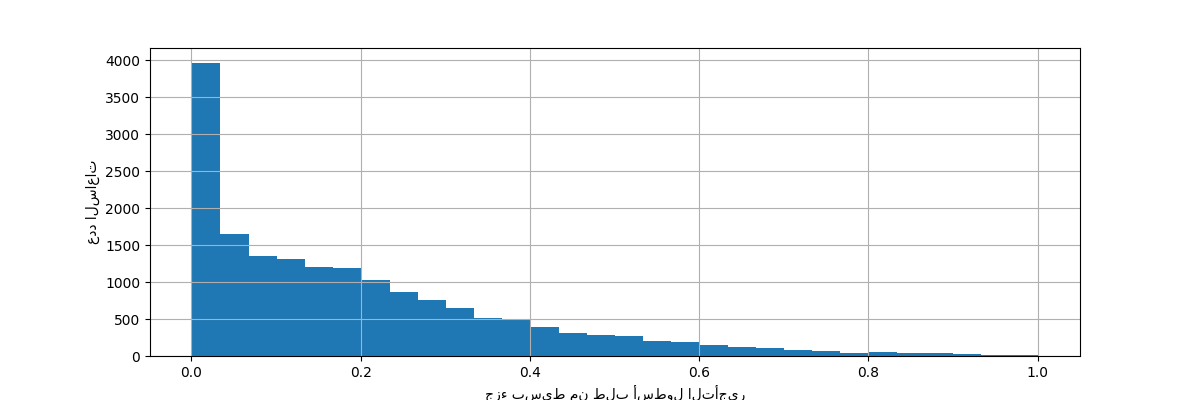
دعونا نعيد قياس متغير الهدف (عدد تأجيرات الدراجات بالساعة) للتنبؤ بطلب نسبي بحيث يكون من السهل تفسير متوسط الخطأ المطلق كجزء بسيط من الحد الأقصى للطلب.
ملاحظة
يقلل أسلوب الملاءمة للنماذج المستخدمة في هذا الدفتر جميعًا من متوسط الخطأ التربيعي لتقدير المتوسط الشرطي. ومع ذلك، سيُقدِّر الخطأ المطلق الوسيط الشرطي.
ومع ذلك، عند الإبلاغ عن مقاييس الأداء على مجموعة الاختبار في المناقشة، نختار التركيز على متوسط الخطأ المطلق بدلاً من متوسط الخطأ التربيعي (الجذر) لأنه من الأسهل تفسيرها. لاحظ، مع ذلك، أنه في هذه الدراسة، فإن أفضل النماذج لمقياس واحد هي أيضًا الأفضل من حيث المقياس الآخر.
y = df["count"] / df["count"].max()
fig, ax = plt.subplots(figsize=(12, 4))
y.hist(bins=30, ax=ax)
_ = ax.set(
xlabel="جزء بسيط من طلب أسطول التأجير",
ylabel="عدد الساعات",
)
إطار بيانات ميزة الإدخال هو سجل كل ساعة بعلامات زمنية للمتغيرات التي تصف أحوال الطقس. يتضمن كلاً من المتغيرات الرقمية والفئوية. لاحظ أنه قد تم بالفعل توسيع معلومات الوقت إلى عدة أعمدة تكميلية.
X = df.drop("count", axis="columns")
X
ملاحظة
إذا كانت معلومات الوقت موجودة فقط كعمود تاريخ أو عمود تاريخ ووقت، فكان من الممكن توسيعها إلى ساعة في اليوم، ويوم في الأسبوع، ويوم في الشهر، وشهر في السنة باستخدام pandas: https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#time-date-components
نستعرض الآن توزيع المتغيرات الفئوية، بدءًا
من "weather":
X["weather"].value_counts()
weather
clear 11413
misty 4544
rain 1419
heavy_rain 3
Name: count, dtype: int64
نظرًا لوجود 3 أحداث "heavy_rain" فقط، لا يمكننا استخدام هذه الفئة لـ
تدريب نماذج التعلم الآلي مع التحقق المتبادل. بدلاً من ذلك، نبسط
التمثيل عن طريق دمجها في فئة "rain".
X["weather"] = (
X["weather"]
.astype(object)
.replace(to_replace="heavy_rain", value="rain")
.astype("category")
)
X["weather"].value_counts()
weather
clear 11413
misty 4544
rain 1422
Name: count, dtype: int64
كما هو متوقع، فإن متغير "season" متوازن جيدًا:
X["season"].value_counts()
season
fall 4496
summer 4409
spring 4242
winter 4232
Name: count, dtype: int64
التحقق المتبادل على أساس الوقت#
نظرًا لأن مجموعة البيانات هي سجل أحداث مرتب زمنيًا (طلب كل ساعة)، فسنستخدم مُقسِّمًا للتحقق المتبادل حساسًا للوقت لتقييم نموذج التنبؤ بالطلب الخاص بنا بأكبر قدر ممكن من الواقعية. نستخدم فجوة لمدة يومين بين جانب التدريب وجانب الاختبار من عمليات التقسيم. نقوم أيضًا بتحديد حجم مجموعة التدريب لجعل أداء طيات التحقق المتبادل أكثر استقرارًا.
يجب أن تكون 1000 نقطة بيانات اختبار كافية لتحديد أداء النموذج. يُمثل هذا أقل بقليل من شهر ونصف من بيانات الاختبار المتجاورة:
ts_cv = TimeSeriesSplit(
n_splits=5,
gap=48,
max_train_size=10000,
test_size=1000,
)
دعونا نفحص يدويًا التقسيمات المختلفة للتحقق من أن
TimeSeriesSplit يعمل كما نتوقع، بدءًا من التقسيم الأول:
all_splits = list(ts_cv.split(X, y))
train_0, test_0 = all_splits[0]
X.iloc[test_0]
X.iloc[train_0]
نفحص الآن التقسيم الأخير:
train_4, test_4 = all_splits[4]
X.iloc[test_4]
X.iloc[train_4]
كل شيء على ما يرام. نحن الآن جاهزون لإجراء بعض النمذجة التنبؤية!
تعزيز التدرج#
غالبًا ما يكون انحدار تعزيز التدرج مع أشجار القرار مرنًا بما يكفي لـ معالجة البيانات الجدولية غير المتجانسة بكفاءة مع مزيج من الميزات الفئوية و الرقمية طالما أن عدد العينات كبير بما يكفي.
هنا، نستخدم
HistGradientBoostingRegressor الحديث مع دعم أصلي
للميزات الفئوية. لذلك، نحتاج فقط إلى تعيين
categorical_features="from_dtype" بحيث تُعتبر الميزات ذات نوع البيانات الفئوية
ميزات فئوية. كمرجع، نستخرج الميزات الفئوية من إطار البيانات بناءً على
نوع البيانات. تستخدم الأشجار الداخلية قاعدة تقسيم شجرة مخصصة لهذه الميزات.
لا تحتاج المتغيرات الرقمية إلى معالجة مسبقة، ومن أجل البساطة، نجرب فقط المعلمات الفائقة الافتراضية لهذا النموذج:
gbrt = HistGradientBoostingRegressor(
categorical_features="from_dtype", random_state=42)
categorical_columns = X.columns[X.dtypes == "category"]
print("الميزات الفئوية:", categorical_columns.tolist())
الميزات الفئوية: ['season', 'holiday', 'workingday', 'weather']
دعونا نُقيِّم نموذج تعزيز التدرج الخاص بنا باستخدام متوسط الخطأ المطلق للطلب النسبي في المتوسط عبر 5 تقسيمات للتحقق المتبادل على أساس الوقت:
def evaluate(model, X, y, cv, model_prop=None, model_step=None):
cv_results = cross_validate(
model,
X,
y,
cv=cv,
scoring=["neg_mean_absolute_error", "neg_root_mean_squared_error"],
return_estimator=model_prop is not None,
)
if model_prop is not None:
if model_step is not None:
values = [
getattr(m[model_step], model_prop) for m in cv_results["estimator"]
]
else:
values = [getattr(m, model_prop) for m in cv_results["estimator"]]
print(f"متوسط model.{model_prop} = {np.mean(values)}")
mae = -cv_results["test_neg_mean_absolute_error"]
rmse = -cv_results["test_neg_root_mean_squared_error"]
print(
f"متوسط الخطأ المطلق: {mae.mean():.3f} +/- {mae.std():.3f}\n"
f"جذر متوسط الخطأ التربيعي: {rmse.mean():.3f} +/- {rmse.std():.3f}"
)
evaluate(gbrt, X, y, cv=ts_cv, model_prop="n_iter_")
متوسط model.n_iter_ = 100.0
متوسط الخطأ المطلق: 0.044 +/- 0.003
جذر متوسط الخطأ التربيعي: 0.068 +/- 0.005
نرى أننا قمنا بتعيين max_iter كبيرة بما يكفي بحيث يتم الإيقاف المبكر.
يبلغ متوسط خطأ هذا النموذج حوالي 4 إلى 5٪ من الحد الأقصى للطلب. هذا جيد جدًا للمحاولة الأولى بدون أي ضبط للمعلمات الفائقة! كان علينا فقط توضيح المتغيرات الفئوية. لاحظ أنه يتم تمرير الميزات ذات الصلة بالوقت كما هي، أي بدون معالجتها. لكن هذه ليست مشكلة كبيرة للنماذج المستندة إلى الشجرة لأنها تستطيع تعلم علاقة غير رتيبة بين ميزات الإدخال الترتيبية والهدف.
هذا ليس هو الحال بالنسبة لنماذج الانحدار الخطي كما سنرى في ما يلي.
الانحدار الخطي الساذج#
كالمعتاد بالنسبة للنماذج الخطية، يجب ترميز المتغيرات الفئوية بشكل أحادي الاتجاه.
من أجل الاتساق، نقوم بقياس الميزات الرقمية على نفس النطاق 0-1 باستخدام
MinMaxScaler، على الرغم من أن هذا لا يؤثر
على النتائج كثيرًا في هذه الحالة لأنها بالفعل على مقاييس قابلة للمقارنة:
one_hot_encoder = OneHotEncoder(handle_unknown="ignore", sparse_output=False)
alphas = np.logspace(-6, 6, 25)
naive_linear_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
],
remainder=MinMaxScaler(),
),
RidgeCV(alphas=alphas),
)
evaluate(
naive_linear_pipeline, X, y, cv=ts_cv, model_prop="alpha_", model_step="ridgecv"
)
متوسط model.alpha_ = 2.7298221281347037
متوسط الخطأ المطلق: 0.142 +/- 0.014
جذر متوسط الخطأ التربيعي: 0.184 +/- 0.020
من المؤكد أن alpha_ المحددة موجودة في نطاقنا المحدد.
الأداء ليس جيدًا: متوسط الخطأ حوالي 14٪ من الحد الأقصى للطلب. هذا أعلى بثلاث مرات من متوسط خطأ نموذج تعزيز التدرج. يمكننا أن نشك في أن الترميز الأصلي الساذج (تم قياسه ببساطة من الحد الأدنى إلى الحد الأقصى) للميزات الدورية ذات الصلة بالوقت قد يمنع نموذج الانحدار الخطي من الاستفادة بشكل صحيح من معلومات الوقت: لا يُنمذج الانحدار الخطي تلقائيًا العلاقات غير الرتيبة بين ميزات الإدخال والهدف. يجب هندسة المصطلحات غير الخطية في الإدخال.
على سبيل المثال، يمنع الترميز الرقمي الأولي لميزة "hour" النموذج
الخطي من التعرف على أن زيادة الساعة في الصباح من 6
إلى 8 يجب أن يكون لها تأثير إيجابي قوي على عدد تأجيرات الدراجات بينما
يجب أن يكون للزيادة ذات الحجم المماثل في المساء من 18 إلى 20 تأثير
سلبي قوي على العدد المتوقع لتأجيرات الدراجات.
الخطوات الزمنية كفئات#
نظرًا لأن ميزات الوقت مُرمَّزة بطريقة منفصلة باستخدام أعداد صحيحة (24 قيمة فريدة في ميزة "hours")، يمكننا أن نقرر التعامل مع هذه كمتغيرات فئوية باستخدام ترميز أحادي الاتجاه وبالتالي تجاهل أي افتراض ضمني بترتيب قيم الساعة.
يمنح استخدام الترميز الأحادي الاتجاه لميزات الوقت النموذج الخطي مرونة أكبر بكثير حيث نُقدم ميزة إضافية واحدة لكل مستوى زمني منفصل.
one_hot_linear_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("one_hot_time", one_hot_encoder, ["hour", "weekday", "month"]),
],
remainder=MinMaxScaler(),
),
RidgeCV(alphas=alphas),
)
evaluate(one_hot_linear_pipeline, X, y, cv=ts_cv)
متوسط الخطأ المطلق: 0.099 +/- 0.011
جذر متوسط الخطأ التربيعي: 0.131 +/- 0.011
يبلغ متوسط معدل الخطأ لهذا النموذج 10٪ وهو أفضل بكثير من استخدام الترميز الأصلي (الترتيبي) لميزة الوقت، مما يؤكد حدسنا بأن نموذج الانحدار الخطي يستفيد من المرونة المضافة لعدم معالجة تقدم الوقت بطريقة رتيبة.
ومع ذلك، يُسبب هذا عددًا كبيرًا جدًا من الميزات الجديدة. إذا تم تمثيل وقت
اليوم بالدقائق منذ بداية اليوم بدلاً من
الساعات، لكان الترميز الأحادي الاتجاه قد أدخل 1440 ميزة بدلاً من 24.
قد يُسبب هذا بعض التكيف الزائد الكبير. لتجنب ذلك، يمكننا استخدام
sklearn.preprocessing.KBinsDiscretizer بدلاً من ذلك لإعادة تصنيف عدد
مستويات المتغيرات الترتيبية أو الرقمية الدقيقة مع الاستمرار
في الاستفادة من مزايا التعبير غير الرتيب للترميز
الأحادي الاتجاه.
أخيرًا، نلاحظ أيضًا أن الترميز الأحادي الاتجاه يتجاهل تمامًا ترتيب مستويات الساعة بينما قد يكون هذا تحيزًا استقرائيًا مثيرًا للاهتمام للحفاظ عليه إلى حد ما. في ما يلي، نحاول استكشاف ترميز سلس وغير رتيب يحافظ محليًا على الترتيب النسبي لميزات الوقت.
الميزات المثلثية#
كمحاولة أولى، يمكننا محاولة ترميز كل من هذه الميزات الدورية باستخدام تحويل الجيب وجيب التمام مع الفترة المقابلة.
يتم تحويل كل ميزة زمنية ترتيبية إلى ميزتين تُرمِّزان معًا معلومات مكافئة بطريقة غير رتيبة، والأهم من ذلك بدون أي قفزة بين القيمة الأولى والأخيرة للنطاق الدوري.
def sin_transformer(period):
return FunctionTransformer(lambda x: np.sin(x / period * 2 * np.pi))
def cos_transformer(period):
return FunctionTransformer(lambda x: np.cos(x / period * 2 * np.pi))
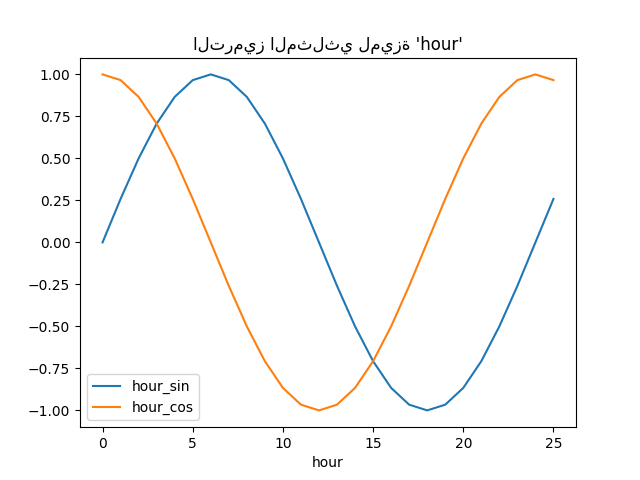
دعونا نتصور تأثير توسيع الميزة هذا على بعض بيانات الساعة التركيبية مع القليل من الاستقراء بعد الساعة = 23:
hour_df = pd.DataFrame(
np.arange(26).reshape(-1, 1),
columns=["hour"],
)
hour_df["hour_sin"] = sin_transformer(24).fit_transform(hour_df)["hour"]
hour_df["hour_cos"] = cos_transformer(24).fit_transform(hour_df)["hour"]
hour_df.plot(x="hour")
_ = plt.title("الترميز المثلثي لميزة 'hour'")
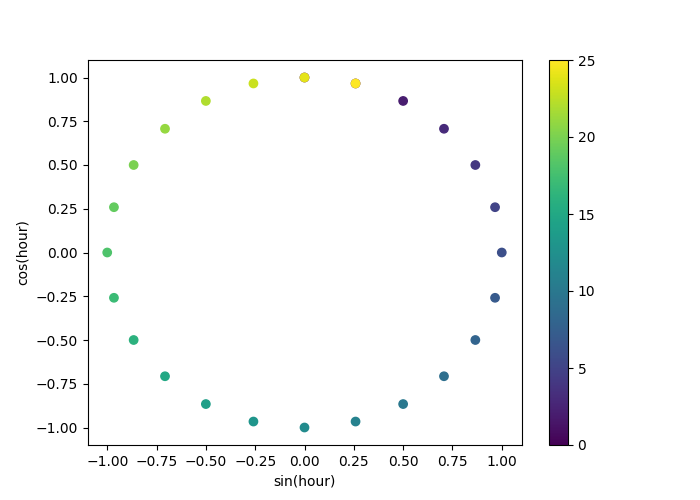
دعونا نستخدم مخطط تشتت ثنائي الأبعاد مع الساعات المُرمَّزة كألوان لنرى بشكل أفضل كيف يُعيِّن هذا التمثيل ساعات اليوم الأربع والعشرين إلى مساحة ثنائية الأبعاد، تُشبه نوعًا من إصدار ساعة تناظرية لمدة 24 ساعة. لاحظ أن الساعة "الخامسة والعشرين" يتم تعيينها مرة أخرى إلى الساعة الأولى بسبب الطبيعة الدورية لتمثيل الجيب/جيب التمام.
fig, ax = plt.subplots(figsize=(7, 5))
sp = ax.scatter(hour_df["hour_sin"], hour_df["hour_cos"], c=hour_df["hour"])
ax.set(
xlabel="sin(hour)",
ylabel="cos(hour)",
)
_ = fig.colorbar(sp)
يمكننا الآن بناء خط أنابيب لاستخراج الميزات باستخدام هذه الاستراتيجية:
cyclic_cossin_transformer = ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("month_sin", sin_transformer(12), ["month"]),
("month_cos", cos_transformer(12), ["month"]),
("weekday_sin", sin_transformer(7), ["weekday"]),
("weekday_cos", cos_transformer(7), ["weekday"]),
("hour_sin", sin_transformer(24), ["hour"]),
("hour_cos", cos_transformer(24), ["hour"]),
],
remainder=MinMaxScaler(),
)
cyclic_cossin_linear_pipeline = make_pipeline(
cyclic_cossin_transformer,
RidgeCV(alphas=alphas),
)
evaluate(cyclic_cossin_linear_pipeline, X, y, cv=ts_cv)
متوسط الخطأ المطلق: 0.125 +/- 0.014
جذر متوسط الخطأ التربيعي: 0.166 +/- 0.020
أداء نموذج الانحدار الخطي الخاص بنا مع هندسة الميزات البسيطة هذه أفضل قليلاً من استخدام ميزات الوقت الترتيبية الأصلية ولكنه أسوأ من استخدام ميزات الوقت المُرمَّزة بشكل أحادي الاتجاه. سنُحلل المزيد من الأسباب المحتملة لهذه النتيجة المخيبة للآمال في نهاية هذا الدفتر.
ميزات сплаين الدورية#
يمكننا تجربة ترميز بديل لميزات الوقت الدورية ذات الصلة باستخدام تحويلات сплаين مع عدد كبير بما يكفي من сплаين، ونتيجة لذلك، عدد أكبر من الميزات الموسعة مقارنة بتحويل الجيب/جيب التمام:
def periodic_spline_transformer(period, n_splines=None, degree=3):
if n_splines is None:
n_splines = period
n_knots = n_splines + 1 # دوري و include_bias هو True
return SplineTransformer(
degree=degree,
n_knots=n_knots,
knots=np.linspace(0, period, n_knots).reshape(n_knots, 1),
extrapolation="periodic",
include_bias=True,
)
مرة أخرى، دعونا نتصور تأثير توسيع الميزة هذا على بعض بيانات الساعة التركيبية مع القليل من الاستقراء بعد الساعة = 23:
hour_df = pd.DataFrame(
np.linspace(0, 26, 1000).reshape(-1, 1),
columns=["hour"],
)
splines = periodic_spline_transformer(24, n_splines=12).fit_transform(hour_df)
splines_df = pd.DataFrame(
splines,
columns=[f"spline_{i}" for i in range(splines.shape[1])],
)
pd.concat([hour_df, splines_df], axis="columns").plot(
x="hour", cmap=plt.cm.tab20b)
_ = plt.title("ترميز قائم على сплаين الدوري لميزة 'hour'")
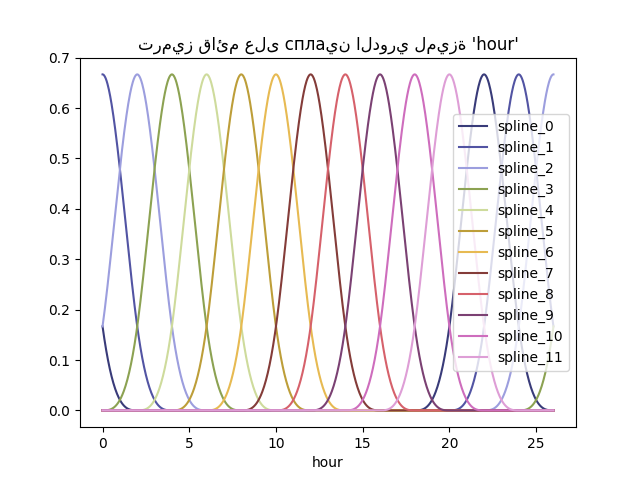
بفضل استخدام معلمة extrapolation="periodic"، نلاحظ
أن ترميز الميزة يظل سلسًا عند الاستقراء إلى ما بعد منتصف الليل.
يمكننا الآن بناء خط أنابيب تنبؤي باستخدام استراتيجية هندسة الميزات الدورية البديلة هذه.
من الممكن استخدام عدد أقل من сплаين من المستويات المنفصلة لهذه القيم الترتيبية. هذا يجعل الترميز القائم على сплаين أكثر كفاءة من الترميز الأحادي الاتجاه مع الحفاظ على معظم التعبيرية:
cyclic_spline_transformer = ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("cyclic_month", periodic_spline_transformer(
12, n_splines=6), ["month"]),
("cyclic_weekday", periodic_spline_transformer(
7, n_splines=3), ["weekday"]),
("cyclic_hour", periodic_spline_transformer(
24, n_splines=12), ["hour"]),
],
remainder=MinMaxScaler(),
)
cyclic_spline_linear_pipeline = make_pipeline(
cyclic_spline_transformer,
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_linear_pipeline, X, y, cv=ts_cv)
متوسط الخطأ المطلق: 0.097 +/- 0.011
جذر متوسط الخطأ التربيعي: 0.132 +/- 0.013
تُمكِّن ميزات сплаين النموذج الخطي من الاستفادة بنجاح من الميزات الدورية ذات الصلة بالوقت وتقليل الخطأ من ~ 14٪ إلى ~ 10٪ من الحد الأقصى للطلب، وهو ما يُشبه ما لاحظناه مع الميزات المُرمَّزة بشكل أحادي الاتجاه.
التحليل النوعي لتأثير الميزات على تنبؤات النموذج الخطي#
هنا، نريد تصور تأثير اختيارات هندسة الميزات على الشكل المتعلق بالوقت للتنبؤات.
للقيام بذلك، نعتبر تقسيمًا عشوائيًا قائمًا على الوقت لمقارنة التنبؤات على مجموعة من نقاط البيانات المحتفظ بها.
naive_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
naive_linear_predictions = naive_linear_pipeline.predict(X.iloc[test_0])
one_hot_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
one_hot_linear_predictions = one_hot_linear_pipeline.predict(X.iloc[test_0])
cyclic_cossin_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_cossin_linear_predictions = cyclic_cossin_linear_pipeline.predict(
X.iloc[test_0])
cyclic_spline_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_spline_linear_predictions = cyclic_spline_linear_pipeline.predict(
X.iloc[test_0])
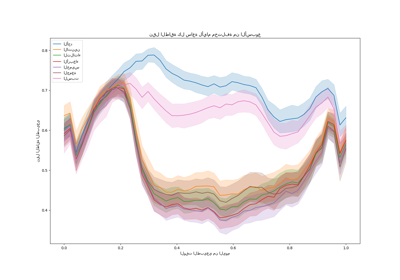
نقوم بتصور هذه التنبؤات عن طريق التكبير على آخر 96 ساعة (4 أيام) من مجموعة الاختبار للحصول على بعض الأفكار النوعية:
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(12, 4))
fig.suptitle("التنبؤات بواسطة النماذج الخطية")
ax.plot(
y.iloc[test_0].values[last_hours],
"x-",
alpha=0.2,
label="الطلب الفعلي",
color="black",
)
ax.plot(naive_linear_predictions[last_hours],
"x-", label="ميزات الوقت الترتيبي")
ax.plot(
cyclic_cossin_linear_predictions[last_hours],
"x-",
label="ميزات الوقت المثلثية",
)
ax.plot(
cyclic_spline_linear_predictions[last_hours],
"x-",
label="ميزات الوقت القائمة على сплаين",
)
ax.plot(
one_hot_linear_predictions[last_hours],
"x-",
label="ميزات الوقت أحادية الاتجاه",
)
_ = ax.legend()
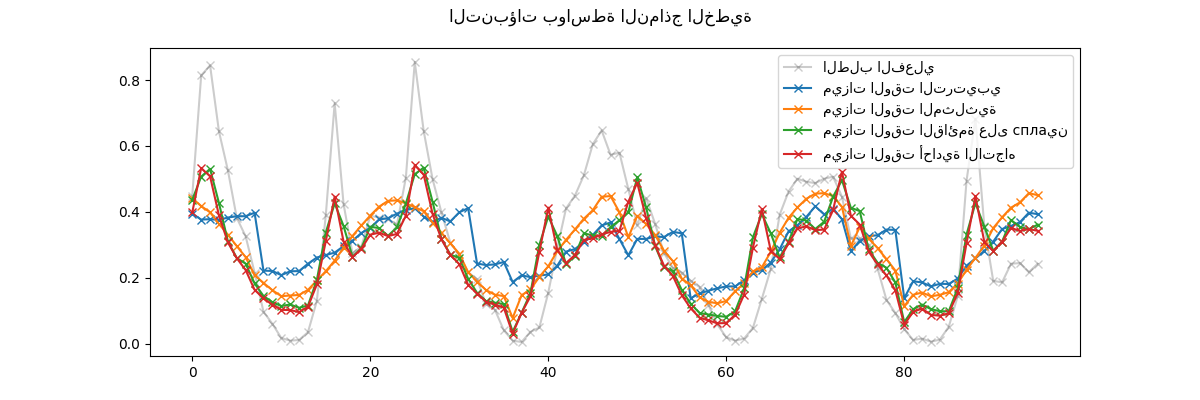
يمكننا استخلاص الاستنتاجات التالية من الرسم البياني أعلاه:
ميزات الوقت الترتيبية الأولية مشكلة لأنها لا تلتقط الدورية الطبيعية: نلاحظ قفزة كبيرة في التنبؤات في نهاية كل يوم عندما تنتقل ميزات الساعة من 23 إلى 0. يمكننا توقع قطع أثرية مماثلة في نهاية كل أسبوع أو كل عام.
كما هو متوقع، الميزات المثلثية (الجيب وجيب التمام) ليس لديها هذه الانقطاعات في منتصف الليل، لكن نموذج الانحدار الخطي يفشل في الاستفادة من هذه الميزات لنمذجة التغيرات داخل اليوم بشكل صحيح. يمكن أن يؤدي استخدام الميزات المثلثية للتوافقيات الأعلى أو الميزات المثلثية الإضافية للفترة الطبيعية ذات المراحل المختلفة إلى إصلاح هذه المشكلة.
تُصلح الميزات الدورية القائمة على сплаين هاتين المشكلتين في وقت واحد: فهي تمنح النموذج الخطي مزيدًا من التعبيرية من خلال تمكينه من التركيز على ساعات محددة بفضل استخدام 12 сплаين. علاوة على ذلك، يفرض خيار
extrapolation="periodic"تمثيلًا سلسًا بينhour=23وhour=0.تتصرف الميزات المُرمَّزة بشكل أحادي الاتجاه بشكل مشابه للميزات الدورية القائمة على сплаين ولكنها أكثر حدة: على سبيل المثال، يمكنها نمذجة ذروة الصباح خلال أيام الأسبوع بشكل أفضل نظرًا لأن هذه الذروة تستمر أقل من ساعة. ومع ذلك، سنرى في ما يلي أن ما يمكن أن يكون ميزة للنماذج الخطية ليس بالضرورة للنماذج الأكثر تعبيرية.
يمكننا أيضًا مقارنة عدد الميزات التي استخرجها كل خط أنابيب لهندسة الميزات:
naive_linear_pipeline[:-1].transform(X).shape
(17379, 19)
one_hot_linear_pipeline[:-1].transform(X).shape
(17379, 59)
cyclic_cossin_linear_pipeline[:-1].transform(X).shape
(17379, 22)
cyclic_spline_linear_pipeline[:-1].transform(X).shape
(17379, 37)
يؤكد هذا أن استراتيجيات الترميز الأحادي الاتجاه والترميز القائم على сплаين تُنشئ ميزات أكثر بكثير لتمثيل الوقت من البدائل، مما يمنح بدوره النموذج الخطي في المراحل النهائية مزيدًا من المرونة (درجات الحرية) لتجنب نقص الملاءمة.
أخيرًا، نلاحظ أنه لا يمكن لأي من النماذج الخطية تقريب الطلب الحقيقي على تأجير الدراجات، خاصة بالنسبة للقمم التي يمكن أن تكون حادة جدًا في ساعات الذروة خلال أيام العمل ولكنها أكثر تسطحًا خلال عطلات نهاية الأسبوع: أكثر النماذج الخطية دقة بناءً على сплаين أو الترميز الأحادي الاتجاه تميل إلى التنبؤ بقمم تأجير الدراجات المتعلقة بالتنقل حتى في عطلات نهاية الأسبوع و التقليل من تقدير الأحداث المتعلقة بالتنقل خلال أيام العمل.
تكشف أخطاء التنبؤ المنهجية هذه عن شكل من أشكال نقص الملاءمة ويمكن تفسيرها من خلال عدم وجود مصطلحات تفاعل بين الميزات، على سبيل المثال "workingday" والميزات المشتقة من "hours". سيتم معالجة هذه المشكلة في القسم التالي.
نمذجة التفاعلات الزوجية مع ميزات сплаين ومتعددة الحدود#
لا تلتقط النماذج الخطية تلقائيًا تأثيرات التفاعل بين ميزات
الإدخال. لا يساعد ذلك في أن بعض الميزات غير خطية بشكل هامشي كما هو
الحال مع الميزات التي تم إنشاؤها بواسطة SplineTransformer (أو الترميز
الأحادي الاتجاه أو التصنيف).
ومع ذلك، من الممكن استخدام فئة PolynomialFeatures على ساعات مُرمَّزة
بـ сплаين خشنة الحبيبات لنمذجة تفاعل "workingday"/"hours"
صراحةً بدون إدخال عدد كبير جدًا من المتغيرات الجديدة:
hour_workday_interaction = make_pipeline(
ColumnTransformer(
[
("cyclic_hour", periodic_spline_transformer(
24, n_splines=8), ["hour"]),
("workingday", FunctionTransformer(
lambda x: x == "True"), ["workingday"]),
]
),
PolynomialFeatures(degree=2, interaction_only=True, include_bias=False),
)
ثم يتم دمج هذه الميزات مع تلك المحسوبة بالفعل في خط أنابيب сплаين السابق. يمكننا ملاحظة تحسن كبير في الأداء عن طريق نمذجة هذا التفاعل الزوجي صراحةً:
cyclic_spline_interactions_pipeline = make_pipeline(
FeatureUnion(
[
("marginal", cyclic_spline_transformer),
("interactions", hour_workday_interaction),
]
),
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_interactions_pipeline, X, y, cv=ts_cv)
متوسط الخطأ المطلق: 0.078 +/- 0.009
جذر متوسط الخطأ التربيعي: 0.104 +/- 0.009
نمذجة تفاعلات الميزات غير الخطية باستخدام النوى#
سلَّط التحليل السابق الضوء على الحاجة إلى نمذجة التفاعلات بين
"workingday" و "hours". مثال آخر على مثل هذا التفاعل غير الخطي
الذي نود نمذجته هو تأثير المطر
الذي قد لا يكون هو نفسه خلال أيام العمل وعطلات نهاية الأسبوع والأعياد
على سبيل المثال.
لنمذجة كل هذه التفاعلات، يمكننا إما استخدام توسيع متعدد الحدود على جميع الميزات الهامشية مرة واحدة، بعد توسيعها القائم على сплаين. ومع ذلك، سيُنشئ هذا عددًا تربيعيًا من الميزات التي يمكن أن تُسبب مشكلات في التكيف الزائد وقابلية التتبع الحسابي.
بدلاً من ذلك، يمكننا استخدام طريقة Nyström لحساب توسيع نواة متعدد الحدود تقريبي. دعونا نجرب هذا الأخير:
cyclic_spline_poly_pipeline = make_pipeline(
cyclic_spline_transformer,
Nystroem(kernel="poly", degree=2, n_components=300, random_state=0),
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_poly_pipeline, X, y, cv=ts_cv)
متوسط الخطأ المطلق: 0.053 +/- 0.002
جذر متوسط الخطأ التربيعي: 0.076 +/- 0.004
نلاحظ أن هذا النموذج يمكن أن ينافس تقريبًا أداء أشجار التعزيز المتدرج بمتوسط خطأ حوالي 5٪ من الحد الأقصى للطلب.
لاحظ أنه على الرغم من أن الخطوة الأخيرة من خط الأنابيب هذا هي نموذج انحدار خطي، فإن الخطوات الوسيطة مثل استخراج ميزة сплаين وتقريب نواة Nyström غير خطية للغاية. نتيجة لذلك، يكون خط الأنابيب المركب أكثر تعبيرية من نموذج الانحدار الخطي البسيط ذي الميزات الأولية.
من أجل الاكتمال، نقوم أيضًا بتقييم مزيج من الترميز الأحادي الاتجاه وتقريب النواة:
one_hot_poly_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("one_hot_time", one_hot_encoder, ["hour", "weekday", "month"]),
],
remainder="passthrough",
),
Nystroem(kernel="poly", degree=2, n_components=300, random_state=0),
RidgeCV(alphas=alphas),
)
evaluate(one_hot_poly_pipeline, X, y, cv=ts_cv)
متوسط الخطأ المطلق: 0.082 +/- 0.006
جذر متوسط الخطأ التربيعي: 0.111 +/- 0.011
بينما كانت الميزات المُرمَّزة بشكل أحادي الاتجاه تنافسية مع الميزات القائمة على сплаين عند استخدام نماذج خطية، لم يعد هذا هو الحال عند استخدام تقريب منخفض الرتبة لنواة غير خطية: يمكن تفسير ذلك من خلال حقيقة أن ميزات сплаين أكثر سلاسة وتسمح لتقريب النواة بالعثور عل
Total running time of the script: (0 minutes 16.698 seconds)
Related examples