ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

التعلم القابل للتطوير مع تقريب نواة متعددة الحدود#

يوضح هذا المثال استخدام PolynomialCountSketch لتوليد تقريبات مساحة ميزات نواة متعددة الحدود بكفاءة. يتم استخدام هذا لتدريب المصنفات الخطية التي تقارب دقة التصنيفات المُكَرَّسَة.

نستخدم مجموعة بيانات Covtype [2]، محاولين إعادة إنتاج التجارب على الورقة الأصلية لـ Tensor Sketch [1]، أي الخوارزمية التي ينفذها PolynomialCountSketch.

أولاً، نحسب دقة مصنف خطي على الميزات الأصلية. ثم، نقوم بتدريب المصنفات الخطية على أعداد مختلفة من الميزات (n_components) التي يولدها PolynomialCountSketch، مما يقارب دقة مصنف مُكَرَّس بطريقة قابلة للتطوير.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

إعداد البيانات#

تحميل مجموعة بيانات Covtype، والتي تحتوي على 581,012 عينة مع 54 ميزة لكل منها، موزعة على 6 فئات. هدف هذه المجموعة من البيانات هو التنبؤ بنوع الغطاء الحرج من المتغيرات الكارتوجرافية فقط (لا توجد بيانات مستشعرة عن بعد). بعد التحميل، نحولها إلى مشكلة تصنيف ثنائي لمطابقة إصدار مجموعة البيانات في صفحة LIBSVM [2]، والتي كانت هي المستخدمة في [1].

from sklearn.datasets import fetch_covtype

X, y = fetch_covtype(return_X_y=True)

y[y != 2] = 0
y[y == 2] = 1  # سنحاول فصل الفئة 2 عن الفئات الست الأخرى.

تقسيم البيانات#

هنا نختار 5,000 عينة للتدريب و10,000 للاختبار. لتكرار نتائج الورقة الأصلية لـ Tensor Sketch، اختر 100,000 للتدريب.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=5_000, test_size=10_000, random_state=42
)

تطبيع الميزات#

الآن نقوم بتصغير الميزات إلى النطاق [0, 1] لمطابقة تنسيق مجموعة البيانات في صفحة LIBSVM، ثم نقوم بتطبيعها إلى طول الوحدة كما هو الحال في الورقة الأصلية لـ Tensor Sketch [1].

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler, Normalizer

mm = make_pipeline(MinMaxScaler(), Normalizer())
X_train = mm.fit_transform(X_train)
X_test = mm.transform(X_test)

إنشاء نموذج خط الأساس#

كتدريب خط الأساس، نقوم بتدريب SVM الخطي على الميزات الأصلية وطباعة الدقة. نقوم أيضًا بقياس وتخزين الدقة وأوقات التدريب لرسمها لاحقًا.

import time

from sklearn.svm import LinearSVC

results = {}

lsvm = LinearSVC()
start = time.time()
lsvm.fit(X_train, y_train)
lsvm_time = time.time() - start
lsvm_score = 100 * lsvm.score(X_test, y_test)

results["LSVM"] = {"time": lsvm_time, "score": lsvm_score}
print(f"Linear SVM score on raw features: {lsvm_score:.2f}%")

Linear SVM score on raw features: 75.62%

إنشاء نموذج تقريب النواة#

ثم نقوم بتدريب SVM الخطية على الميزات التي يولدها PolynomialCountSketch مع قيم مختلفة لـ n_components، مما يُظهر أن هذه التقريبات لميزات النواة تحسن دقة التصنيف الخطي. في سيناريوهات التطبيق النموذجية، يجب أن يكون n_components أكبر من عدد الميزات في التمثيل المدخل لتحقيق تحسن فيما يتعلق بالتصنيف الخطي. كقاعدة عامة، يتم تحقيق الأمثل لتقييم الدرجات / تكلفة وقت التشغيل عادةً عند n_components = 10 * n_features، على الرغم من أن هذا قد يعتمد على مجموعة البيانات المحددة التي يتم التعامل معها. لاحظ أنه، نظرًا لأن العينات الأصلية تحتوي على 54 ميزة، فإن خريطة الميزات الصريحة لنواة متعددة الحدود من الدرجة الرابعة سيكون لها حوالي 8.5 مليون ميزة (بدقة، 54^4). بفضل PolynomialCountSketch، يمكننا تكثيف معظم المعلومات التمييزية لمساحة الميزات تلك في تمثيل أكثر إحكاما. على الرغم من أننا نجري التجربة مرة واحدة فقط (n_runs = 1) في هذا المثال، في الممارسة العملية يجب تكرار التجربة عدة مرات للتعويض عن الطبيعة العشوائية لـ PolynomialCountSketch.

from sklearn.kernel_approximation import PolynomialCountSketch

n_runs = 1
N_COMPONENTS = [250, 500, 1000, 2000]

for n_components in N_COMPONENTS:
    ps_lsvm_time = 0
    ps_lsvm_score = 0
    for _ in range(n_runs):
        pipeline = make_pipeline(
            PolynomialCountSketch(n_components=n_components, degree=4),
            LinearSVC(),
        )

        start = time.time()
        pipeline.fit(X_train, y_train)
        ps_lsvm_time += time.time() - start
        ps_lsvm_score += 100 * pipeline.score(X_test, y_test)

    ps_lsvm_time /= n_runs
    ps_lsvm_score /= n_runs

    results[f"LSVM + PS({n_components})"] = {
        "time": ps_lsvm_time,
        "score": ps_lsvm_score,
    }
    print(
        f"Linear SVM score on {n_components} PolynomialCountSketch "
        + f"features: {ps_lsvm_score:.2f}%"
    )

Linear SVM score on 250 PolynomialCountSketch features: 76.34%
Linear SVM score on 500 PolynomialCountSketch features: 77.47%
Linear SVM score on 1000 PolynomialCountSketch features: 77.81%
Linear SVM score on 2000 PolynomialCountSketch features: 78.31%

إنشاء نموذج SVM المُكَرَّس#

تدريب SVM المُكَرَّس لمشاهدة مدى جودة PolynomialCountSketch في تقريب أداء النواة. بالطبع، قد يستغرق هذا بعض الوقت، حيث أن فئة SVC لديها قابلية للتطوير نسبيًا. هذا هو السبب في أن مقاربات النواة مفيدة جدًا:

from sklearn.svm import SVC

ksvm = SVC(C=500.0, kernel="poly", degree=4, coef0=0, gamma=1.0)

start = time.time()
ksvm.fit(X_train, y_train)
ksvm_time = time.time() - start
ksvm_score = 100 * ksvm.score(X_test, y_test)

results["KSVM"] = {"time": ksvm_time, "score": ksvm_score}
print(f"Kernel-SVM score on raw features: {ksvm_score:.2f}%")

Kernel-SVM score on raw features: 79.78%

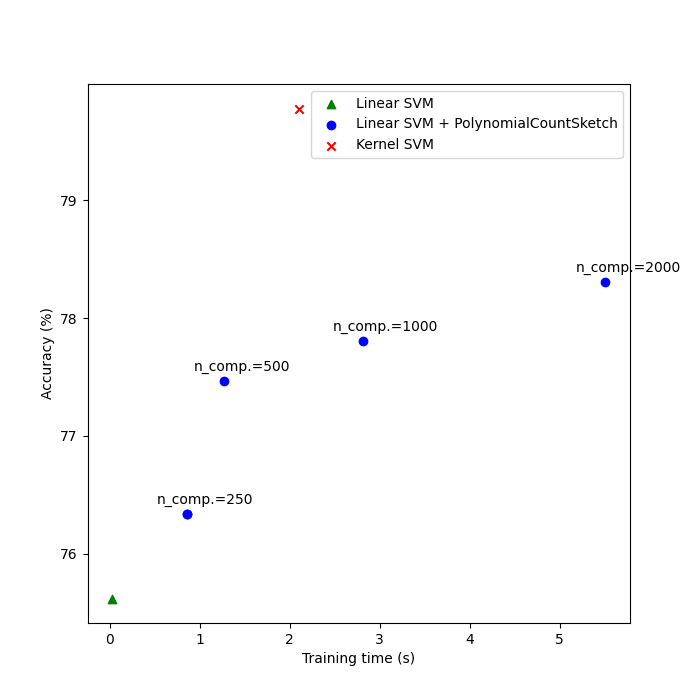
مقارنة النتائج#

أخيرًا، قم برسم نتائج الطرق المختلفة مقابل أوقات تدريبها. كما يمكننا أن نرى، يحقق SVM المُكَرَّس دقة أعلى، لكن وقت تدريبه أكبر بكثير، والأهم من ذلك، سينمو بشكل أسرع إذا زاد عدد عينات التدريب.

import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(7, 7))
ax.scatter(
    [
        results["LSVM"]["time"],
    ],
    [
        results["LSVM"]["score"],
    ],
    label="Linear SVM",
    c="green",
    marker="^",
)

ax.scatter(
    [
        results["LSVM + PS(250)"]["time"],
    ],
    [
        results["LSVM + PS(250)"]["score"],
    ],
    label="Linear SVM + PolynomialCountSketch",
    c="blue",
)

for n_components in N_COMPONENTS:
    ax.scatter(
        [
            results[f"LSVM + PS({n_components})"]["time"],
        ],
        [
            results[f"LSVM + PS({n_components})"]["score"],
        ],
        c="blue",
    )
    ax.annotate(
        f"n_comp.={n_components}",
        (
            results[f"LSVM + PS({n_components})"]["time"],
            results[f"LSVM + PS({n_components})"]["score"],
        ),
        xytext=(-30, 10),
        textcoords="offset pixels",
    )

ax.scatter(
    [
        results["KSVM"]["time"],
    ],
    [
        results["KSVM"]["score"],
    ],
    label="Kernel SVM",
    c="red",
    marker="x",
)

ax.set_xlabel("Training time (s)")
ax.set_ylabel("Accuracy (%)")
ax.legend()
plt.show()

المراجع#

[1] Pham, Ninh and Rasmus Pagh. "Fast and scalable polynomial kernels via explicit feature maps." KDD '13 (2013). https://doi.org/10.1145/2487575.2487591

[2] LIBSVM binary datasets repository https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html

Total running time of the script: (1 minutes 31.362 seconds)