ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
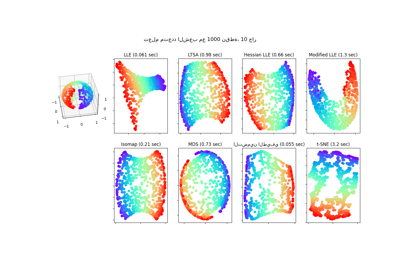
مقارنة طرق تعلم متعدد الشعب#
توضيح لخفض الأبعاد على مجموعة بيانات المنحنى S مع طرق تعلم متعدد الشعب المختلفة.
لنقاش ومقارنة هذه الخوارزميات، انظر صفحة وحدة متعدد الشعب
لمثال مماثل، حيث يتم تطبيق الطرق على مجموعة بيانات كروية، انظر طرق تعلم متعدد الشعب على كرة مقطوعة
لاحظ أن الغرض من MDS هو إيجاد تمثيل منخفض الأبعاد للبيانات (هنا 2D) حيث تحترم المسافات جيدًا المسافات في الفضاء الأصلي عالي الأبعاد، على عكس أخرى خوارزميات تعلم متعدد الشعب، فهي لا تسعى إلى تمثيل متماثل للبيانات في الفضاء منخفض الأبعاد.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
إعداد مجموعة البيانات#
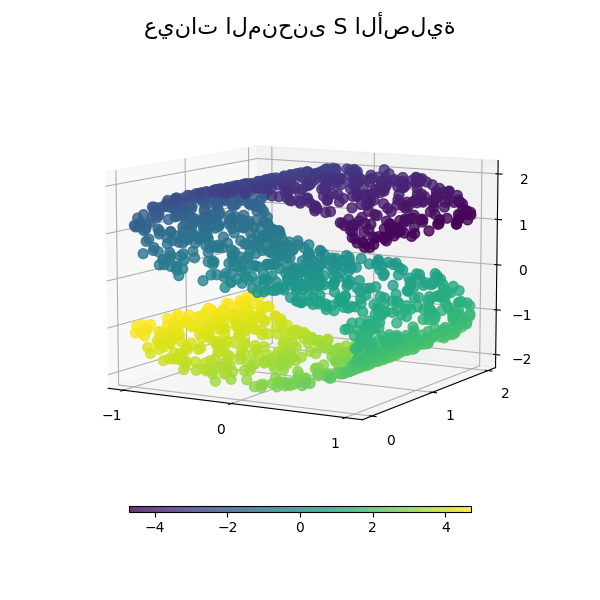
نبدأ بتوليد مجموعة بيانات المنحنى S.
import matplotlib.pyplot as plt
# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d # noqa: F401
from matplotlib import ticker
from sklearn import datasets, manifold
n_samples = 1500
S_points, S_color = datasets.make_s_curve(n_samples, random_state=0)
لنلقِ نظرة على البيانات الأصلية. ونعرّف أيضًا بعض الدوال المساعدة، والتي سنستخدمها لاحقًا.
def plot_3d(points, points_color, title):
x, y, z = points.T
fig, ax = plt.subplots(
figsize=(6, 6),
facecolor="white",
tight_layout=True,
subplot_kw={"projection": "3d"},
)
fig.suptitle(title, size=16)
col = ax.scatter(x, y, z, c=points_color, s=50, alpha=0.8)
ax.view_init(azim=-60, elev=9)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
ax.zaxis.set_major_locator(ticker.MultipleLocator(1))
fig.colorbar(col, ax=ax, orientation="horizontal", shrink=0.6, aspect=60, pad=0.01)
plt.show()
def plot_2d(points, points_color, title):
fig, ax = plt.subplots(figsize=(3, 3), facecolor="white", constrained_layout=True)
fig.suptitle(title, size=16)
add_2d_scatter(ax, points, points_color)
plt.show()
def add_2d_scatter(ax, points, points_color, title=None):
x, y = points.T
ax.scatter(x, y, c=points_color, s=50, alpha=0.8)
ax.set_title(title)
ax.xaxis.set_major_formatter(ticker.NullFormatter())
ax.yaxis.set_major_formatter(ticker.NullFormatter())
plot_3d(S_points, S_color, "عينات المنحنى S الأصلية")
تعريف خوارزميات لتعلم متعدد الشعب#
تعلم متعدد الشعب هو نهج لخفض الأبعاد غير الخطي. تعتمد خوارزميات هذه المهمة على فكرة أن أبعاد العديد من مجموعات البيانات مرتفعة بشكل مصطنع فقط.
اقرأ المزيد في دليل المستخدم.
n_neighbors = 12 # الجوار الذي يتم استخدامه لاستعادة الهيكل الخطي المحلي
n_components = 2 # عدد الإحداثيات لمتعدد الشعب
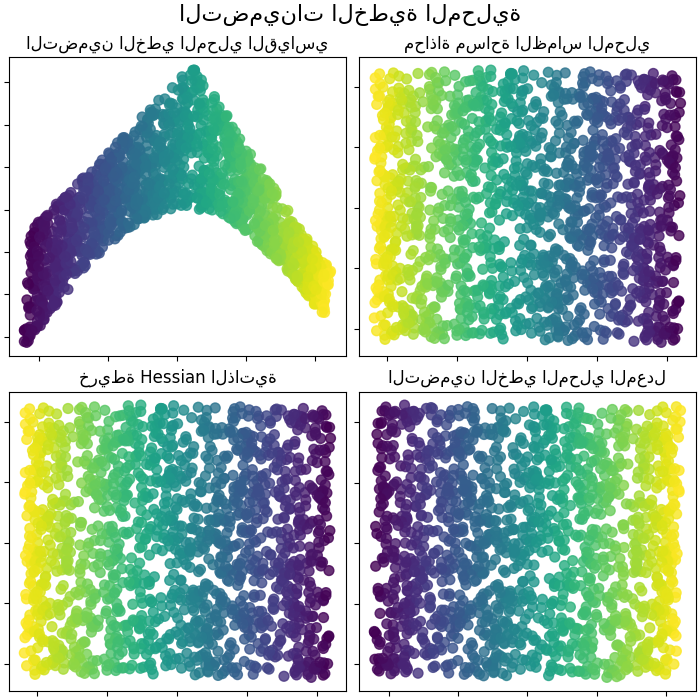
تضمينات خطية محليًا#
يمكن اعتبار التضمين الخطي المحلي (LLE) سلسلة من تحليلات المكونات الرئيسية المحلية التي تتم مقارنتها عالميًا لإيجاد أفضل تضمين غير خطي. اقرأ المزيد في دليل المستخدم.
params = {
"n_neighbors": n_neighbors,
"n_components": n_components,
"eigen_solver": "auto",
"random_state": 0,
}
lle_standard = manifold.LocallyLinearEmbedding(method="standard", **params)
S_standard = lle_standard.fit_transform(S_points)
lle_ltsa = manifold.LocallyLinearEmbedding(method="ltsa", **params)
S_ltsa = lle_ltsa.fit_transform(S_points)
lle_hessian = manifold.LocallyLinearEmbedding(method="hessian", **params)
S_hessian = lle_hessian.fit_transform(S_points)
lle_mod = manifold.LocallyLinearEmbedding(method="modified", **params)
S_mod = lle_mod.fit_transform(S_points)
fig, axs = plt.subplots(
nrows=2, ncols=2, figsize=(7, 7), facecolor="white", constrained_layout=True
)
fig.suptitle("التضمينات الخطية المحلية", size=16)
lle_methods = [
("التضمين الخطي المحلي القياسي", S_standard),
("محاذاة مساحة الظماس المحلي", S_ltsa),
("خريطة Hessian الذاتية", S_hessian),
("التضمين الخطي المحلي المعدل", S_mod),
]
for ax, method in zip(axs.flat, lle_methods):
name, points = method
add_2d_scatter(ax, points, S_color, name)
plt.show()
تضمين Isomap#
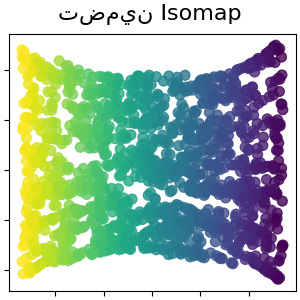
خفض الأبعاد غير الخطي من خلال التعيين المتساوي القياس. يبحث Isomap عن تضمين منخفض الأبعاد يحافظ على المسافات الجيوديسية بين جميع النقاط. اقرأ المزيد في دليل المستخدم.
isomap = manifold.Isomap(n_neighbors=n_neighbors, n_components=n_components, p=1)
S_isomap = isomap.fit_transform(S_points)
plot_2d(S_isomap, S_color, "تضمين Isomap")
القياس متعدد الأبعاد#
يبحث القياس متعدد الأبعاد (MDS) عن تمثيل منخفض الأبعاد للبيانات حيث تحترم المسافات جيدًا المسافات في الفضاء الأصلي عالي الأبعاد. اقرأ المزيد في دليل المستخدم.
md_scaling = manifold.MDS(
n_components=n_components,
max_iter=50,
n_init=4,
random_state=0,
normalized_stress=False,
)
S_scaling = md_scaling.fit_transform(S_points)
plot_2d(S_scaling, S_color, "القياس متعدد الأبعاد")

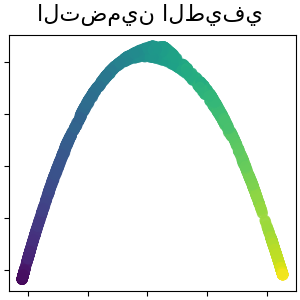
التضمين الطيفي لخفض الأبعاد غير الخطي#
يستخدم هذا التنفيذ خرائط Laplacian الذاتية، والتي تجد تمثيلًا منخفض الأبعاد للبيانات باستخدام تحليل طيفي لمصفوفة Laplacian للرسم البياني. اقرأ المزيد في دليل المستخدم.
spectral = manifold.SpectralEmbedding(
n_components=n_components, n_neighbors=n_neighbors, random_state=42
)
S_spectral = spectral.fit_transform(S_points)
plot_2d(S_spectral, S_color, "التضمين الطيفي")
تضمين الجوار العشوائي الموزع على شكل حرف T#
يحول أوجه التشابه بين نقاط البيانات إلى احتمالات مشتركة و يحاول تقليل اختلاف Kullback-Leibler بين الاحتمالات المشتركة للتضمين منخفض الأبعاد والبيانات عالية الأبعاد. لدى t-SNE دالة تكلفة ليست محدبة، أي مع تهيئات أولية مختلفة يمكننا الحصول على نتائج مختلفة. اقرأ المزيد في دليل المستخدم.
t_sne = manifold.TSNE(
n_components=n_components,
perplexity=30,
init="random",
max_iter=250,
random_state=0,
)
S_t_sne = t_sne.fit_transform(S_points)
plot_2d(S_t_sne, S_color, "تضمين الجوار العشوائي \n الموزع على شكل حرف T")

Total running time of the script: (0 minutes 17.568 seconds)
Related examples

تعلم متعدد الشعب على الأرقام المكتوبة بخط اليد: التضمين الخطي المحلي، Isomap...
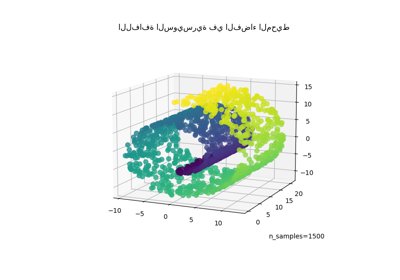
خفض اللفافة السويسرية واللفافة السويسرية ذات الثقب