ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

هيكلة سوق الأسهم المرئية#

يستخدم هذا المثال عدة تقنيات تعلم غير خاضعة للإشراف لاستخراج هيكل سوق الأسهم من الاختلافات في الاقتباسات التاريخية.

الكمية التي نستخدمها هي التغير اليومي في سعر الاقتباس: الاقتباسات المرتبطة تميل إلى التقلب فيما يتعلق ببعضها البعض خلال يوم.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

استرجاع البيانات من الإنترنت#

البيانات من 2003 - 2008. هذا هادئ بشكل معقول: (ليس منذ وقت طويل بحيث نحصل على شركات التكنولوجيا الفائقة، وقبل تحطم 2008). يمكن الحصول على هذا النوع من البيانات التاريخية من واجهات برمجة التطبيقات مثل data.nasdaq.com و alphavantage.co.

import sys

import numpy as np
import pandas as pd

symbol_dict = {
    "TOT": "Total",
    "XOM": "Exxon",
    "CVX": "Chevron",
    "COP": "ConocoPhillips",
    "VLO": "Valero Energy",
    "MSFT": "Microsoft",
    "IBM": "IBM",
    "TWX": "Time Warner",
    "CMCSA": "Comcast",
    "CVC": "Cablevision",
    "YHOO": "Yahoo",
    "DELL": "Dell",
    "HPQ": "HP",
    "AMZN": "Amazon",
    "TM": "Toyota",
    "CAJ": "Canon",
    "SNE": "Sony",
    "F": "Ford",
    "HMC": "Honda",
    "NAV": "Navistar",
    "NOC": "Northrop Grumman",
    "BA": "Boeing",
    "KO": "Coca Cola",
    "MMM": "3M",
    "MCD": "McDonald's",
    "PEP": "Pepsi",
    "K": "Kellogg",
    "UN": "Unilever",
    "MAR": "Marriott",
    "PG": "Procter Gamble",
    "CL": "Colgate-Palmolive",
    "GE": "General Electrics",
    "WFC": "Wells Fargo",
    "JPM": "JPMorgan Chase",
    "AIG": "AIG",
    "AXP": "American express",
    "BAC": "Bank of America",
    "GS": "Goldman Sachs",
    "AAPL": "Apple",
    "SAP": "SAP",
    "CSCO": "Cisco",
    "TXN": "Texas Instruments",
    "XRX": "Xerox",
    "WMT": "Wal-Mart",
    "HD": "Home Depot",
    "GSK": "GlaxoSmithKline",
    "PFE": "Pfizer",
    "SNY": "Sanofi-Aventis",
    "NVS": "Novartis",
    "KMB": "Kimberly-Clark",
    "R": "Ryder",
    "GD": "General Dynamics",
    "RTN": "Raytheon",
    "CVS": "CVS",
    "CAT": "Caterpillar",
    "DD": "DuPont de Nemours",
}


symbols, names = np.array(sorted(symbol_dict.items())).T

quotes = []

for symbol in symbols:
    print("Fetching quote history for %r" % symbol, file=sys.stderr)
    url = (
        "https://raw.githubusercontent.com/scikit-learn/examples-data/"
        "master/financial-data/{}.csv"
    )
    quotes.append(pd.read_csv(url.format(symbol)))

close_prices = np.vstack([q["close"] for q in quotes])
open_prices = np.vstack([q["open"] for q in quotes])

# التغيرات اليومية في الاقتباسات هي ما تحمل معظم المعلومات
variation = close_prices - open_prices

Fetching quote history for 'AAPL'
Fetching quote history for 'AIG'
Fetching quote history for 'AMZN'
Fetching quote history for 'AXP'
Fetching quote history for 'BA'
Fetching quote history for 'BAC'
Fetching quote history for 'CAJ'
Fetching quote history for 'CAT'
Fetching quote history for 'CL'
Fetching quote history for 'CMCSA'
Fetching quote history for 'COP'
Fetching quote history for 'CSCO'
Fetching quote history for 'CVC'
Fetching quote history for 'CVS'
Fetching quote history for 'CVX'
Fetching quote history for 'DD'
Fetching quote history for 'DELL'
Fetching quote history for 'F'
Fetching quote history for 'GD'
Fetching quote history for 'GE'
Fetching quote history for 'GS'
Fetching quote history for 'GSK'
Fetching quote history for 'HD'
Fetching quote history for 'HMC'
Fetching quote history for 'HPQ'
Fetching quote history for 'IBM'
Fetching quote history for 'JPM'
Fetching quote history for 'K'
Fetching quote history for 'KMB'
Fetching quote history for 'KO'
Fetching quote history for 'MAR'
Fetching quote history for 'MCD'
Fetching quote history for 'MMM'
Fetching quote history for 'MSFT'
Fetching quote history for 'NAV'
Fetching quote history for 'NOC'
Fetching quote history for 'NVS'
Fetching quote history for 'PEP'
Fetching quote history for 'PFE'
Fetching quote history for 'PG'
Fetching quote history for 'R'
Fetching quote history for 'RTN'
Fetching quote history for 'SAP'
Fetching quote history for 'SNE'
Fetching quote history for 'SNY'
Fetching quote history for 'TM'
Fetching quote history for 'TOT'
Fetching quote history for 'TWX'
Fetching quote history for 'TXN'
Fetching quote history for 'UN'
Fetching quote history for 'VLO'
Fetching quote history for 'WFC'
Fetching quote history for 'WMT'
Fetching quote history for 'XOM'
Fetching quote history for 'XRX'
Fetching quote history for 'YHOO'

تعلم هيكل الرسم البياني#

نستخدم تقدير معكوس التباين النادر للعثور على الاقتباسات التي مترابطة شرطياً على الآخرين. على وجه التحديد، يعطينا معكوس التباين النادر رسم بياني، وهو قائمة من الاتصالات. لكل رمز، الرموز التي يتصل بها هي تلك المفيدة لشرح تقلباته.

from sklearn import covariance

alphas = np.logspace(-1.5, 1, num=10)
edge_model = covariance.GraphicalLassoCV(alphas=alphas)

# توحيد سلسلة الوقت: استخدام الارتباطات بدلاً من التباين
# السابق أكثر كفاءة لاستعادة الهيكل
X = variation.copy().T
X /= X.std(axis=0)
edge_model.fit(X)

GraphicalLassoCV(alphas=array([ 0.03162278,  0.05994843,  0.11364637,  0.21544347,  0.40842387,
        0.77426368,  1.46779927,  2.7825594 ,  5.27499706, 10.        ]))

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

التجميع باستخدام انتشار الانتماء#

نستخدم التجميع لجمع الاقتباسات التي تتصرف بشكل مشابه. هنا، من بين تقنيات التجميع المختلفة المتاحة في scikit-learn، نستخدم انتشار التقارب كما أنه لا لا تفرض مجموعات متساوية الحجم، ويمكنها اختيار عدد المجموعات تلقائيًا من البيانات.

لاحظ أن هذا يعطينا مؤشرًا مختلفًا عن الرسم البياني، حيث يعكس الرسم البياني العلاقات الشرطية بين المتغيرات، في حين أن التجميع يعكس الخصائص الهامشية: يمكن اعتبار المتغيرات المجمعة معًا كأن لها تأثيرًا مماثلًا على مستوى سوق الأسهم بالكامل.

from sklearn import cluster

_, labels = cluster.affinity_propagation(edge_model.covariance_, random_state=0)
n_labels = labels.max()

for i in range(n_labels + 1):
    print(f"Cluster {i + 1}: {', '.join(names[labels == i])}")

Cluster 1: Apple, Amazon, Yahoo
Cluster 2: Comcast, Cablevision, Time Warner
Cluster 3: ConocoPhillips, Chevron, Total, Valero Energy, Exxon
Cluster 4: Cisco, Dell, HP, IBM, Microsoft, SAP, Texas Instruments
Cluster 5: Boeing, General Dynamics, Northrop Grumman, Raytheon
Cluster 6: AIG, American express, Bank of America, Caterpillar, CVS, DuPont de Nemours, Ford, General Electrics, Goldman Sachs, Home Depot, JPMorgan Chase, Marriott, McDonald's, 3M, Ryder, Wells Fargo, Wal-Mart
Cluster 7: GlaxoSmithKline, Novartis, Pfizer, Sanofi-Aventis, Unilever
Cluster 8: Kellogg, Coca Cola, Pepsi
Cluster 9: Colgate-Palmolive, Kimberly-Clark, Procter Gamble
Cluster 10: Canon, Honda, Navistar, Sony, Toyota, Xerox

تضمين في مساحة ثنائية الأبعاد#

لأغراض العرض، نحتاج إلى وضع الرموز المختلفة على قماش ثنائي الأبعاد. لهذا نستخدم manifold تقنيات لاسترداد تضمين ثنائي الأبعاد. نستخدم محددًا كثيفًا للوصول إلى إمكانية إعادة الإنتاج (يتم بدء arpack مع المتجهات العشوائية التي لا نتحكم فيها). بالإضافة إلى ذلك، نستخدم عدد كبير من الجيران لالتقاط الهيكل واسع النطاق.

# العثور على تضمين منخفض الأبعاد للعرض: العثور على أفضل موضع
# للعقد (الأسهم) على طائرة ثنائية الأبعاد

from sklearn import manifold

node_position_model = manifold.LocallyLinearEmbedding(
    n_components=2, eigen_solver="dense", n_neighbors=6
)

embedding = node_position_model.fit_transform(X.T).T

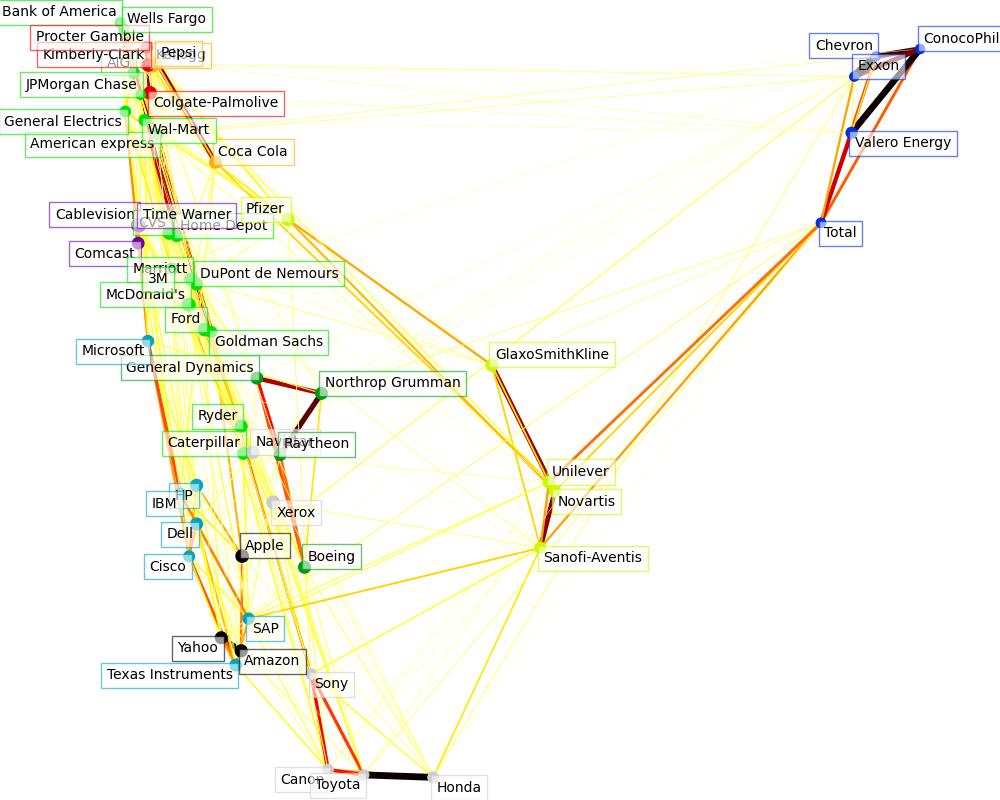
العرض المرئي#

يتم دمج مخرجات النماذج الثلاثة في رسم بياني ثنائي الأبعاد حيث العقد يمثل الأسهم والحافات:

تستخدم تسميات المجموعات لتحديد لون العقد
يستخدم نموذج التباين النادر لعرض قوة الحواف
يستخدم التضمين ثنائي الأبعاد لوضع العقد في الخطة

يحتوي هذا المثال على كمية عادلة من التعليمات البرمجية المتعلقة بالعرض المرئي، حيث العرض المرئي أمر بالغ الأهمية هنا لعرض الرسم البياني. أحد التحديات هو وضع التسميات لتقليل التداخل. لهذا نستخدم خوارزمية تقريبية تعتمد على اتجاه أقرب جار على طول كل المحور.

import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection

plt.figure(1, facecolor="w", figsize=(10, 8))
plt.clf()
ax = plt.axes([0.0, 0.0, 1.0, 1.0])
plt.axis("off")

# رسم رسم بياني للارتباطات الجزئية
partial_correlations = edge_model.precision_.copy()
d = 1 / np.sqrt(np.diag(partial_correlations))
partial_correlations *= d
partial_correlations *= d[:, np.newaxis]
non_zero = np.abs(np.triu(partial_correlations, k=1)) > 0.02

# رسم العقد باستخدام إحداثيات التضمين الخاص بنا
plt.scatter(
    embedding[0], embedding[1], s=100 * d**2, c=labels, cmap=plt.cm.nipy_spectral
)

# رسم الحواف
start_idx, end_idx = np.where(non_zero)
# تتابع (*line0*، *line1*، *line2*)، حيث::
#            linen = (x0, y0)، (x1, y1)، ... (xm, ym)
segments = [
    [embedding[:, start], embedding[:, stop]] for start, stop in zip(start_idx, end_idx)
]
values = np.abs(partial_correlations[non_zero])
lc = LineCollection(
    segments, zorder=0, cmap=plt.cm.hot_r, norm=plt.Normalize(0, 0.7 * values.max())
)
lc.set_array(values)
lc.set_linewidths(15 * values)
ax.add_collection(lc)

# إضافة تسمية لكل عقدة. التحدي هنا هو أننا نريد
# وضع التسميات لتجنب التداخل مع التسميات الأخرى
for index, (name, label, (x, y)) in enumerate(zip(names, labels, embedding.T)):
    dx = x - embedding[0]
    dx[index] = 1
    dy = y - embedding[1]
    dy[index] = 1
    this_dx = dx[np.argmin(np.abs(dy))]
    this_dy = dy[np.argmin(np.abs(dx))]
    if this_dx > 0:
        horizontalalignment = "left"
        x = x + 0.002
    else:
        horizontalalignment = "right"
        x = x - 0.002
    if this_dy > 0:
        verticalalignment = "bottom"
        y = y + 0.002
    else:
        verticalalignment = "top"
        y = y - 0.002
    plt.text(
        x,
        y,
        name,
        size=10,
        horizontalalignment=horizontalalignment,
        verticalalignment=verticalalignment,
        bbox=dict(
            facecolor="w",
            edgecolor=plt.cm.nipy_spectral(label / float(n_labels)),
            alpha=0.6,
        ),
    )

plt.xlim(
    embedding[0].min() - 0.15 * np.ptp(embedding[0]),
    embedding[0].max() + 0.10 * np.ptp(embedding[0]),
)
plt.ylim(
    embedding[1].min() - 0.03 * np.ptp(embedding[1]),
    embedding[1].max() + 0.03 * np.ptp(embedding[1]),
)

plt.show()