ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

تقدير معكوس التغاير النادر#

استخدام أداة تقدير GraphicalLasso لتعلم التغاير والانحراف النادر من عدد صغير من العينات.

لتقدير نموذج احتمالي (مثل النموذج الغاوسي)، فإن تقدير مصفوفة الانحراف، أي مصفوفة معكوس التغاير، هو بنفس أهمية تقدير مصفوفة التغاير. في الواقع، يتم تحديد نموذج غاوسي بواسطة مصفوفة الانحراف.

للحصول على ظروف استرداد مواتية، نقوم بجمع البيانات من نموذج بمصفوفة معكوس تغاير نادرة. بالإضافة إلى ذلك، نضمن أن البيانات ليست مرتبطة للغاية (تحديد أكبر معامل في مصفوفة الانحراف) وأنه لا يوجد معاملات صغيرة في مصفوفة الانحراف التي لا يمكن استردادها. بالإضافة إلى ذلك، مع عدد صغير من الملاحظات، من الأسهل استرداد مصفوفة الارتباط بدلاً من التغاير، وبالتالي نقوم بتصحيح سلسلة الوقت.

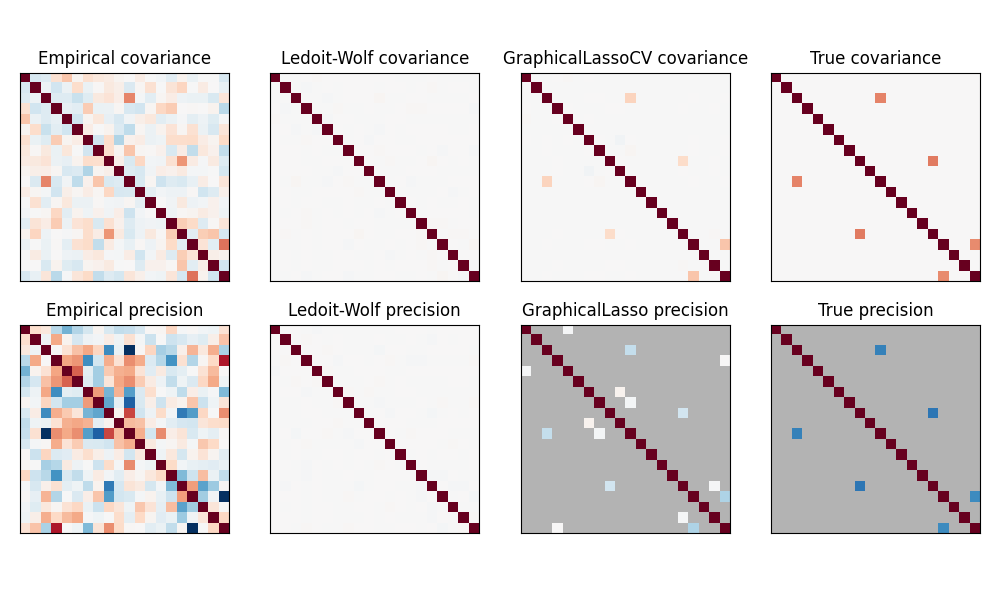
هنا، عدد العينات أكبر قليلاً من عدد الأبعاد، وبالتالي فإن التغاير التجريبي لا يزال قابلًا للعكس. ومع ذلك، بما أن الملاحظات مرتبطة بقوة، فإن مصفوفة التغاير التجريبية سيئة الشرط ونتيجة لذلك، فإن معكوسها - التغاير التجريبي الدقيق - بعيد جدًا عن الحقيقة.

إذا استخدمنا الانكماش l2، كما هو الحال مع أداة تقدير Ledoit-Wolf، حيث أن عدد العينات صغير، نحتاج إلى الانكماش كثيرًا. ونتيجة لذلك، فإن دقة Ledoit-Wolf قريبة جدًا من دقة الحقيقة، والتي ليست بعيدة عن كونها قطريًا، ولكن يتم فقدان البنية خارج القطر.

يمكن لأداة التقدير المعاقب l1 استرداد جزء من هذه البنية خارج القطر. إنها تتعلم الانحراف النادر. إنها غير قادرة على استرداد نمط التفرعات الدقيق: فهي تكتشف الكثير من المعاملات غير الصفرية. ومع ذلك، فإن أعلى المعاملات غير الصفرية المقدرة l1 تتوافق مع المعاملات غير الصفرية في الحقيقة. أخيرًا، فإن معاملات تقدير الانحراف l1 متحيزة نحو الصفر: بسبب العقوبة، فهي جميعها أصغر من قيمة الحقيقة المقابلة، كما يمكن رؤيتها في الشكل.

لاحظ أن نطاق ألوان مصفوفات الانحراف يتم ضبطه لتحسين قابلية قراءة الشكل. لا يتم عرض النطاق الكامل لقيم التغاير التجريبي.

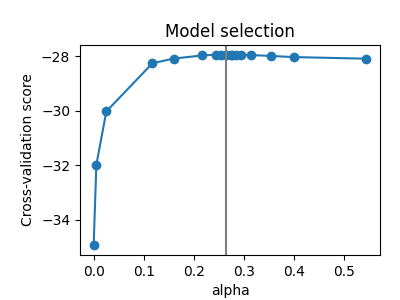
يتم تعيين معامل alpha لأداة GraphicalLasso لتحديد ندرة النموذج بواسطة التحقق الداخلي من الصحة في GraphicalLassoCV. كما يمكن رؤيته في الشكل 2، يتم تكرار الشبكة لحساب درجة التحقق من الصحة في الجوار الأقصى.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

توليد البيانات#

import matplotlib.pyplot as plt
from sklearn.covariance import GraphicalLassoCV, ledoit_wolf
import numpy as np
from scipy import linalg

from sklearn.datasets import make_sparse_spd_matrix

n_samples = 60
n_features = 20

prng = np.random.RandomState(1)
prec = make_sparse_spd_matrix(
    n_features, alpha=0.98, smallest_coef=0.4, largest_coef=0.7, random_state=prng
)
cov = linalg.inv(prec)
d = np.sqrt(np.diag(cov))
cov /= d
cov /= d[:, np.newaxis]
prec *= d
prec *= d[:, np.newaxis]
X = prng.multivariate_normal(np.zeros(n_features), cov, size=n_samples)
X -= X.mean(axis=0)
X /= X.std(axis=0)

تقدير التغاير#

emp_cov = np.dot(X.T, X) / n_samples

model = GraphicalLassoCV()
model.fit(X)
cov_ = model.covariance_
prec_ = model.precision_

lw_cov_, _ = ledoit_wolf(X)
lw_prec_ = linalg.inv(lw_cov_)

رسم النتائج#

plt.figure(figsize=(10, 6))
plt.subplots_adjust(left=0.02, right=0.98)

# رسم التغايرات
covs = [
    ("Empirical", emp_cov),
    ("Ledoit-Wolf", lw_cov_),
    ("GraphicalLassoCV", cov_),
    ("True", cov),
]
vmax = cov_.max()
for i, (name, this_cov) in enumerate(covs):
    plt.subplot(2, 4, i + 1)
    plt.imshow(
        this_cov, interpolation="nearest", vmin=-vmax, vmax=vmax, cmap=plt.cm.RdBu_r
    )
    plt.xticks(())
    plt.yticks(())
    plt.title("%s covariance" % name)
# رسم الانحرافات
precs = [
    ("Empirical", linalg.inv(emp_cov)),
    ("Ledoit-Wolf", lw_prec_),
    ("GraphicalLasso", prec_),
    ("True", prec),
]
vmax = 0.9 * prec_.max()
for i, (name, this_prec) in enumerate(precs):
    ax = plt.subplot(2, 4, i + 5)
    plt.imshow(
        np.ma.masked_equal(this_prec, 0),
        interpolation="nearest",
        vmin=-vmax,
        vmax=vmax,
        cmap=plt.cm.RdBu_r,
    )
    plt.xticks(())
    plt.yticks(())
    plt.title("%s precision" % name)
    if hasattr(ax, "set_facecolor"):
        ax.set_facecolor(".7")
    else:
        ax.set_axis_bgcolor(".7")

Empirical covariance, Ledoit-Wolf covariance, GraphicalLassoCV covariance, True covariance, Empirical precision, Ledoit-Wolf precision, GraphicalLasso precision, True precision

# رسم مقياس اختيار النموذج
plt.figure(figsize=(4, 3))
plt.axes([0.2, 0.15, 0.75, 0.7])
plt.plot(model.cv_results_["alphas"],
         model.cv_results_["mean_test_score"], "o-")
plt.axvline(model.alpha_, color=".5")
plt.title("Model selection")
plt.ylabel("Cross-validation score")
plt.xlabel("alpha")

plt.show()