ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

تقدير التغاير القوي وأهمية مسافات Mahalanobis#

يوضح هذا المثال تقدير التغاير باستخدام مسافات Mahalanobis على بيانات موزعة غاوسيًا.

بالنسبة للبيانات الموزعة غاوسيًا، يمكن حساب مسافة الملاحظة \(x_i\) إلى مركز التوزيع باستخدام مسافة Mahalanobis:

\[d_{(\mu,\Sigma)}(x_i)^2 = (x_i - \mu)^T\Sigma^{-1}(x_i - \mu)\]

حيث \(\mu\) و \(\Sigma\) هما الموقع والتغاير لتوزيعات غاوسية الأساسية.

في الممارسة العملية، يتم استبدال \(\mu\) و \(\Sigma\) ببعض التقديرات. يكون تقدير أقصى احتمال للتغاير القياسي (MLE) حساسًا جدًا لوجود القيم المتطرفة في مجموعة البيانات، وبالتالي، فإن مسافات Mahalanobis اللاحقة هي أيضًا. سيكون من الأفضل استخدام مقدر قوي للتغاير لضمان أن يكون التقدير مقاوماً للملاحظات "الخاطئة" في مجموعة البيانات وأن مسافات Mahalanobis المحسوبة تعكس بدقة التنظيم الحقيقي للملاحظات.

مقدر الحد الأدنى لمحدد التغاير (MCD) هو مقدر قوي، عالي نقطة الانهيار (أي يمكن استخدامه لتقدير مصفوفة التغاير لمجموعات البيانات شديدة التلوث، حتى \(\frac{n_\text{samples}-n_\text{features}-1}{2}\) قيم متطرفة) للتغاير. الفكرة وراء MCD هي إيجاد \(\frac{n_\text{samples}+n_\text{features}+1}{2}\) ملاحظات يكون التغاير التجريبي لها هو المحدد الأصغر، مما ينتج عنه مجموعة فرعية "نقية" من الملاحظات التي يمكن من خلالها حساب التقديرات القياسية للموقع والتغاير. تم تقديم MCD بواسطة P.J.Rousseuw في [1].

يوضح هذا المثال كيف تتأثر مسافات Mahalanobis بالبيانات المتطرفة. الملاحظات المأخوذة من توزيع ملوث لا يمكن تمييزها عن الملاحظات القادمة من التوزيع الحقيقي، التوزيع الغاوسي عند استخدام مسافات Mahalanobis القياسية القائمة على MLE. باستخدام مسافات Mahalanobis القائمة على MCD، يصبح من الممكن تمييز التوزيعين. تشمل التطبيقات المرتبطة بها اكتشاف القيم المتطرفة، تصنيف الملاحظات والتجميع.

ملاحظة

انظر أيضًا تقدير التغاير القوي مقابل التجريبي

المراجع

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

إنشاء البيانات#

أولاً، نقوم بإنشاء مجموعة بيانات من 125 عينة وميزتين. كلا الميزتين موزعتان غاوسية بمتوسط 0 ولكن الميزة 1 لها انحراف معياري يساوي 2 والميزة 2 لها انحراف معياري يساوي 1. بعد ذلك، يتم استبدال 25 عينة بعينات خارجية غاوسية حيث الميزة 1 لها انحراف معياري يساوي 1 والميزة 2 لها انحراف معياري يساوي 7.

import numpy as np

# من أجل نتائج متسقة
np.random.seed(7)

n_samples = 125
n_outliers = 25
n_features = 2

# إنشاء بيانات غاوسية بشكل (125، 2)
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.0
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
# إضافة بعض القيم المتطرفة
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.0
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)

مقارنة النتائج#

أدناه، نقوم بملاءمة مقدرات التغاير القائمة على MCD و MLE لبياناتنا ونطبع مصفوفات التغاير المقدرة. لاحظ أن التباين المقدر للميزة 2 أعلى بكثير مع المقدر القائم على MLE (7.5) من ذلك الخاص بمقدر MCD القوي (1.2). يوضح هذا أن المقدر القوي القائم على MCD أكثر مقاومة لعينات القيم المتطرفة، والتي تم تصميمها لتكون ذات تباين أكبر بكثير في الميزة 2.

import matplotlib.pyplot as plt

from sklearn.covariance import EmpiricalCovariance, MinCovDet

# ملاءمة مقدر MCD قوي للبيانات
robust_cov = MinCovDet().fit(X)
# ملاءمة مقدر MLE للبيانات
emp_cov = EmpiricalCovariance().fit(X)
print(
    "مصفوفة التغاير المقدرة:\nMCD (قوي):\n{}\nMLE:\n{}".format(
        robust_cov.covariance_, emp_cov.covariance_
    )
)

مصفوفة التغاير المقدرة:
MCD (قوي):
[[ 3.26253567e+00 -3.06695631e-03]
 [-3.06695631e-03  1.22747343e+00]]
MLE:
[[ 3.23773583 -0.24640578]
 [-0.24640578  7.51963999]]

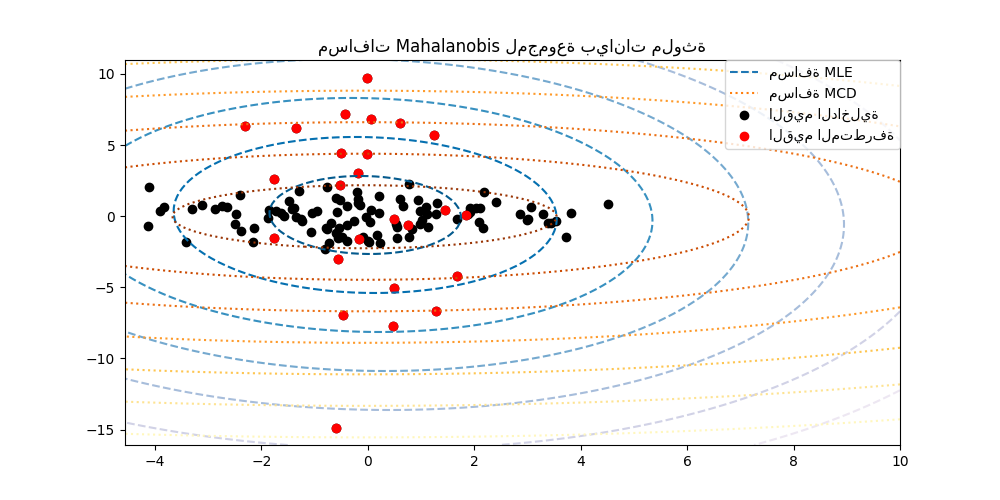
لتوضيح الفرق بشكل أفضل، نرسم خطوط كفاف لمسافات Mahalanobis المحسوبة بكلا الطريقتين. لاحظ أن مسافات Mahalanobis القوية القائمة على MCD تناسب النقاط السوداء الداخلية بشكل أفضل، بينما تتأثر المسافات القائمة على MLE أكثر بالنقاط الحمراء الخارجية.

import matplotlib.lines as mlines

fig, ax = plt.subplots(figsize=(10, 5))
# رسم مجموعة البيانات
inlier_plot = ax.scatter(X[:, 0], X[:, 1], color="black", label="inliers")
outlier_plot = ax.scatter(
    X[:, 0][-n_outliers:], X[:, 1][-n_outliers:], color="red", label="outliers"
)
ax.set_xlim(ax.get_xlim()[0], 10.0)
ax.set_title("مسافات Mahalanobis لمجموعة بيانات ملوثة")

# إنشاء شبكة من قيم الميزة 1 والميزة 2
xx, yy = np.meshgrid(
    np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
    np.linspace(plt.ylim()[0], plt.ylim()[1], 100),
)
zz = np.c_[xx.ravel(), yy.ravel()]
# حساب مسافات Mahalanobis القائمة على MLE للشبكة
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = plt.contour(
    xx, yy, np.sqrt(mahal_emp_cov), cmap=plt.cm.PuBu_r, linestyles="dashed"
)
# حساب مسافات Mahalanobis القائمة على MCD
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = ax.contour(
    xx, yy, np.sqrt(mahal_robust_cov), cmap=plt.cm.YlOrBr_r, linestyles="dotted"
)

# إضافة وسيلة إيضاح
ax.legend(
    [
        mlines.Line2D([], [], color="tab:blue", linestyle="dashed"),
        mlines.Line2D([], [], color="tab:orange", linestyle="dotted"),
        inlier_plot,
        outlier_plot,
    ],
    ["مسافة MLE", "مسافة MCD", "القيم الداخلية", "القيم المتطرفة"],
    loc="upper right",
    borderaxespad=0,
)

plt.show()

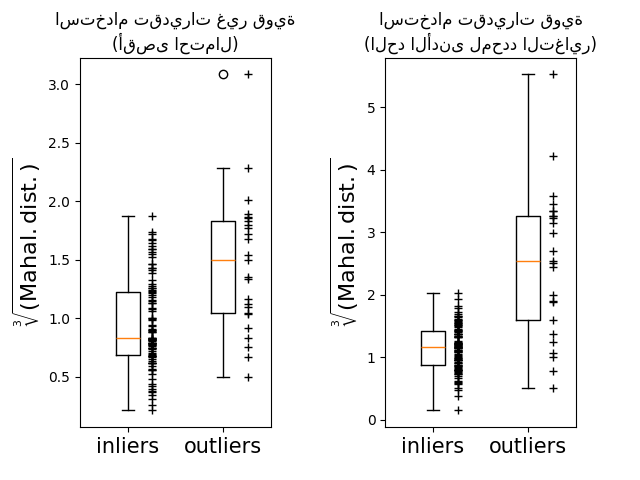
أخيرًا، نسلط الضوء على قدرة مسافات Mahalanobis القائمة على MCD على تمييز القيم المتطرفة. نأخذ الجذر التكعيبي لمسافات Mahalanobis، مما ينتج عنه توزيعات طبيعية تقريبًا (كما اقترح ويلسون وهيلفرتي [2]), ثم ارسم قيم عينات القيم الداخلية والخارجية باستخدام مخططات الصندوق. يكون توزيع عينات القيم المتطرفة أكثر انفصالًا عن توزيع عينات القيم الداخلية لمسافات Mahalanobis القوية القائمة على MCD.

fig, (ax1, ax2) = plt.subplots(1, 2)
plt.subplots_adjust(wspace=0.6)

# حساب الجذر التكعيبي لمسافات MLE Mahalanobis للعينات
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.33)
# رسم مخططات الصندوق
ax1.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=0.25)
# رسم العينات الفردية
ax1.plot(
    np.full(n_samples - n_outliers, 1.26),
    emp_mahal[:-n_outliers],
    "+k",
    markeredgewidth=1,
)
ax1.plot(np.full(n_outliers, 2.26), emp_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax1.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax1.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax1.set_title("استخدام تقديرات غير قوية\n(أقصى احتمال)")

# حساب الجذر التكعيبي لمسافات MCD Mahalanobis للعينات
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.33)
# رسم مخططات الصندوق
ax2.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]], widths=0.25)
# رسم العينات الفردية
ax2.plot(
    np.full(n_samples - n_outliers, 1.26),
    robust_mahal[:-n_outliers],
    "+k",
    markeredgewidth=1,
)
ax2.plot(np.full(n_outliers, 2.26), robust_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax2.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax2.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax2.set_title("استخدام تقديرات قوية\n(الحد الأدنى لمحدد التغاير)")

plt.show()