تأثير تحويل الأهداف في نموذج الانحدار

في هذا المثال، نقدم نظرة عامة على TransformedTargetRegressor. نستخدم مثالين لتوضيح فائدة تحويل الأهداف قبل تعلم نموذج انحدار خطي. يستخدم المثال الأول بيانات تركيبية بينما يعتمد المثال الثاني على مجموعة بيانات منازل Ames.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

from sklearn.model_selection import GridSearchCV
from sklearn.covariance import OAS, LedoitWolf
from sklearn.covariance import ShrunkCovariance, empirical_covariance, log_likelihood
from scipy import linalg
from sklearn.preprocessing import QuantileTransformer
from sklearn.preprocessing import quantile_transform
from sklearn.datasets import fetch_openml
from sklearn.metrics import PredictionErrorDisplay
from sklearn.linear_model import RidgeCV
from sklearn.compose import TransformedTargetRegressor
from sklearn.metrics import median_absolute_error, r2_score
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
import numpy as np
print(__doc__)

مثال تركيبي

يتم إنشاء مجموعة بيانات انحدار عشوائية تركيبية. يتم تعديل الأهداف y بواسطة:

1. ترجمة جميع الأهداف بحيث تكون جميع الإدخالات غير سالبة (عن طريق إضافة القيمة المطلقة لأدنى y) و

2. تطبيق دالة أسية للحصول على أهداف غير خطية لا يمكن ملاءمتها باستخدام نموذج خطي بسيط.

لذلك، سيتم استخدام دالة لوغاريتمية (np.log1p) ودالة أسية (np.expm1) لتحويل الأهداف قبل تدريب نموذج انحدار خطي واستخدامه للتنبؤ.

X, y = make_regression(n_samples=10_000, noise=100, random_state=0)
y = np.expm1((y + abs(y.min())) / 200)
y_trans = np.log1p(y)

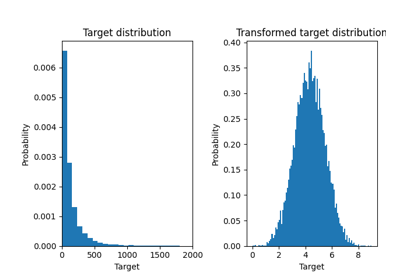
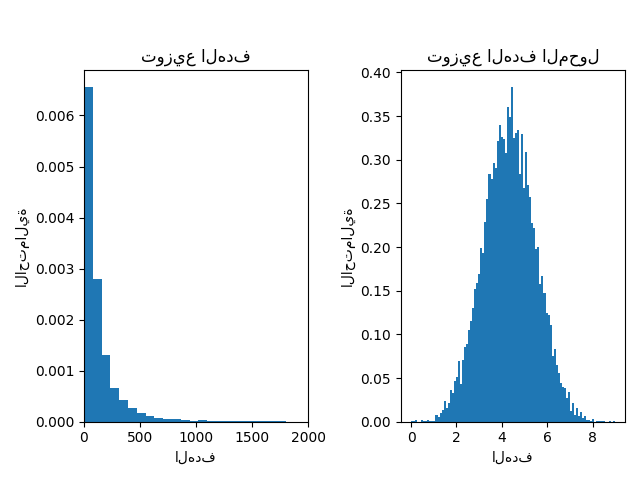
أدناه نرسم دوال كثافة الاحتمال للهدف قبل وبعد تطبيق الدوال اللوغاريتمية.

f, (ax0, ax1) = plt.subplots(1, 2)

ax0.hist(y, bins=100, density=True)
ax0.set_xlim([0, 2000])
ax0.set_ylabel("الاحتمالية")
ax0.set_xlabel("الهدف")
ax0.set_title("توزيع الهدف")

ax1.hist(y_trans, bins=100, density=True)
ax1.set_ylabel("الاحتمالية")
ax1.set_xlabel("الهدف")
ax1.set_title("توزيع الهدف المحول")

f.suptitle("البيانات التركيبية", y=1.05)
plt.tight_layout()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

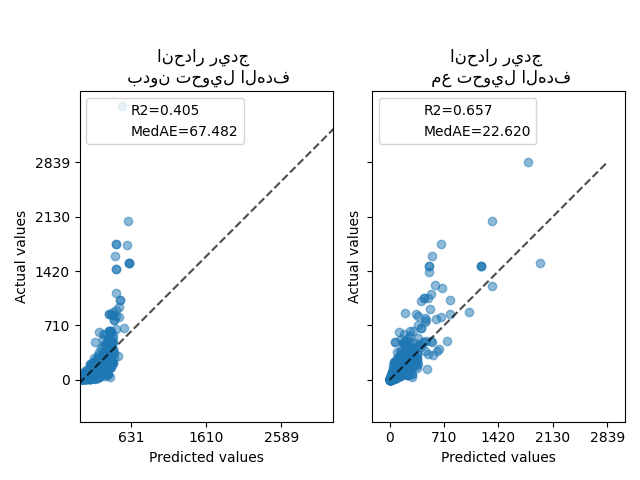
في البداية، سيتم تطبيق نموذج خطي على الأهداف الأصلية. نظرًا لـ اللاخطية، لن يكون النموذج المدرب دقيقًا أثناء التنبؤ. بعد ذلك، يتم استخدام دالة لوغاريتمية لجعل الأهداف خطية، مما يسمح بتنبؤ أفضل حتى مع نموذج خطي مشابه كما هو موضح بواسطة متوسط الخطأ المطلق (MedAE).

def compute_score(y_true, y_pred):
    return {
        "R2": f"{r2_score(y_true, y_pred):.3f}",
        "MedAE": f"{median_absolute_error(y_true, y_pred):.3f}",
    }

f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)

ridge_cv = RidgeCV().fit(X_train, y_train)
y_pred_ridge = ridge_cv.predict(X_test)

ridge_cv_with_trans_target = TransformedTargetRegressor(
    regressor=RidgeCV(), func=np.log1p, inverse_func=np.expm1
).fit(X_train, y_train)
y_pred_ridge_with_trans_target = ridge_cv_with_trans_target.predict(X_test)

PredictionErrorDisplay.from_predictions(
    y_test,
    y_pred_ridge,
    kind="actual_vs_predicted",
    ax=ax0,
    scatter_kwargs={"alpha": 0.5},
)
PredictionErrorDisplay.from_predictions(
    y_test,
    y_pred_ridge_with_trans_target,
    kind="actual_vs_predicted",
    ax=ax1,
    scatter_kwargs={"alpha": 0.5},
)

# إضافة الدرجة في وسيلة الإيضاح لكل محور
for ax, y_pred in zip([ax0, ax1], [y_pred_ridge, y_pred_ridge_with_trans_target]):
    for name, score in compute_score(y_test, y_pred).items():
        ax.plot([], [], " ", label=f"{name}={score}")
    ax.legend(loc="upper left")

ax0.set_title("انحدار ريدج \n بدون تحويل الهدف")
ax1.set_title("انحدار ريدج \n مع تحويل الهدف")
f.suptitle("البيانات التركيبية", y=1.05)
plt.tight_layout()

مجموعة بيانات من العالم الحقيقي

بطريقة مماثلة، يتم استخدام مجموعة بيانات منازل Ames لإظهار تأثير تحويل الأهداف قبل تعلم نموذج. في هذا المثال، الهدف المراد التنبؤ به هو سعر بيع كل منزل.

ames = fetch_openml(name="house_prices", as_frame=True)
# احتفظ بالأعمدة الرقمية فقط
X = ames.data.select_dtypes(np.number)
# إزالة الأعمدة ذات القيم NaN أو Inf
X = X.drop(columns=["LotFrontage", "GarageYrBlt", "MasVnrArea"])
# اجعل السعر بالآلاف من الدولارات
y = ames.target / 1000
y_trans = quantile_transform(
    y.to_frame(), n_quantiles=900, output_distribution="normal", copy=True
).squeeze()

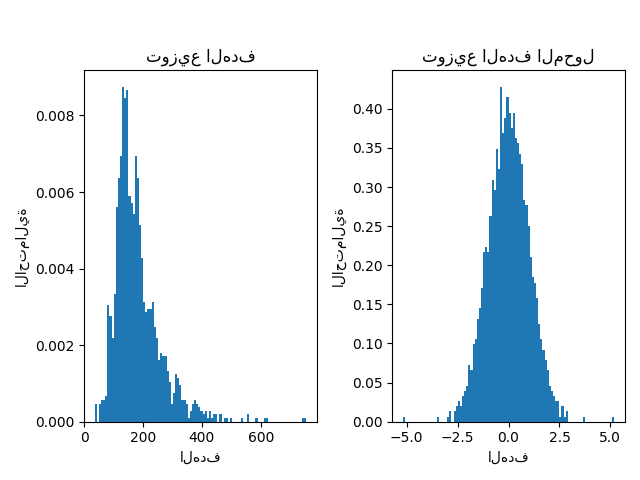
يتم استخدام QuantileTransformer لتطبيع توزيع الهدف قبل تطبيق نموذج RidgeCV.

f, (ax0, ax1) = plt.subplots(1, 2)

ax0.hist(y, bins=100, density=True)
ax0.set_ylabel("الاحتمالية")
ax0.set_xlabel("الهدف")
ax0.set_title("توزيع الهدف")

ax1.hist(y_trans, bins=100, density=True)
ax1.set_ylabel("الاحتمالية")
ax1.set_xlabel("الهدف")
ax1.set_title("توزيع الهدف المحول")

f.suptitle("بيانات منازل Ames: سعر البيع", y=1.05)
plt.tight_layout()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

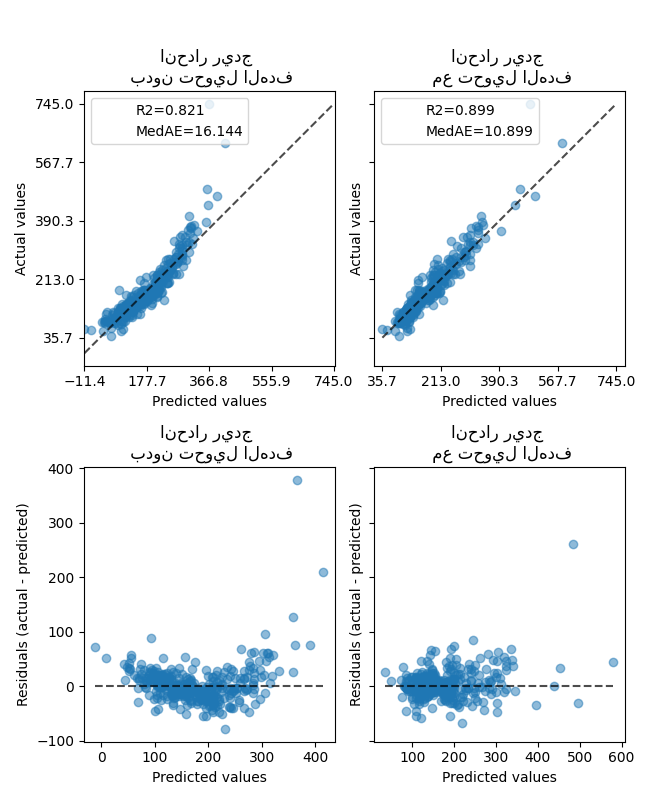
تأثير المحول أضعف من البيانات التركيبية. ومع ذلك، يؤدي التحويل إلى زيادة في \(R^2\) وانخفاض كبير في MedAE. يأخذ مخطط المتبقيات (الهدف المتوقع - الهدف الحقيقي مقابل الهدف المتوقع) بدون تحويل الهدف شكلًا منحنًا يشبه "الابتسامة العكسية" بسبب القيم المتبقية التي تختلف اعتمادًا على قيمة الهدف المتوقع. مع تحويل الهدف، يكون الشكل أكثر خطية مما يشير إلى ملاءمة أفضل للنموذج.

f, (ax0, ax1) = plt.subplots(2, 2, sharey="row", figsize=(6.5, 8))

ridge_cv = RidgeCV().fit(X_train, y_train)
y_pred_ridge = ridge_cv.predict(X_test)

ridge_cv_with_trans_target = TransformedTargetRegressor(
    regressor=RidgeCV(),
    transformer=QuantileTransformer(
        n_quantiles=900, output_distribution="normal"),
).fit(X_train, y_train)
y_pred_ridge_with_trans_target = ridge_cv_with_trans_target.predict(X_test)

# رسم القيم الفعلية مقابل القيم المتوقعة
PredictionErrorDisplay.from_predictions(
    y_test,
    y_pred_ridge,
    kind="actual_vs_predicted",
    ax=ax0[0],
    scatter_kwargs={"alpha": 0.5},
)
PredictionErrorDisplay.from_predictions(
    y_test,
    y_pred_ridge_with_trans_target,
    kind="actual_vs_predicted",
    ax=ax0[1],
    scatter_kwargs={"alpha": 0.5},
)

# إضافة الدرجة في وسيلة الإيضاح لكل محور
for ax, y_pred in zip([ax0[0], ax0[1]], [y_pred_ridge, y_pred_ridge_with_trans_target]):
    for name, score in compute_score(y_test, y_pred).items():
        ax.plot([], [], " ", label=f"{name}={score}")
    ax.legend(loc="upper left")

ax0[0].set_title("انحدار ريدج \n بدون تحويل الهدف")
ax0[1].set_title("انحدار ريدج \n مع تحويل الهدف")


# رسم المتبقيات مقابل القيم المتوقعة
PredictionErrorDisplay.from_predictions(
    y_test,
    y_pred_ridge,
    kind="residual_vs_predicted",
    ax=ax1[0],
    scatter_kwargs={"alpha": 0.5},
)
PredictionErrorDisplay.from_predictions(
    y_test,
    y_pred_ridge_with_trans_target,
    kind="residual_vs_predicted",
    ax=ax1[1],
    scatter_kwargs={"alpha": 0.5},
)
ax1[0].set_title("انحدار ريدج \n بدون تحويل الهدف")
ax1[1].set_title("انحدار ريدج \n مع تحويل الهدف")

f.suptitle("بيانات منازل Ames: سعر البيع", y=1.05)
plt.tight_layout()
plt.show()
"""
=======================================================================
تقدير انكماش التغاير: LedoitWolf مقابل OAS وأقصى احتمال
=======================================================================

عند العمل مع تقدير التغاير، فإن النهج المعتاد هو استخدام
مقدر أقصى احتمال، مثل
:class:`~sklearn.covariance.EmpiricalCovariance`. إنه غير متحيز، أي
يتقارب مع التغاير الحقيقي (السكاني) عند إعطاء العديد من
الملاحظات. ومع ذلك، قد يكون من المفيد أيضًا تنظيمه، من أجل تقليل تباينه؛ وهذا بدوره يؤدي إلى بعض التحيز. يوضح هذا المثال التنظيم البسيط المستخدم في
مقدرات :ref:`shrunk_covariance`. على وجه الخصوص، يركز على كيفية
تعيين مقدار التنظيم، أي كيفية اختيار المفاضلة بين التحيز والتباين.
"""

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

'\n=======================================================================\nتقدير انكماش التغاير: LedoitWolf مقابل OAS وأقصى احتمال\n=======================================================================\n\nعند العمل مع تقدير التغاير، فإن النهج المعتاد هو استخدام\nمقدر أقصى احتمال، مثل\n:class:`~sklearn.covariance.EmpiricalCovariance`. إنه غير متحيز، أي\nيتقارب مع التغاير الحقيقي (السكاني) عند إعطاء العديد من\nالملاحظات. ومع ذلك، قد يكون من المفيد أيضًا تنظيمه، من أجل تقليل تباينه؛ وهذا بدوره يؤدي إلى بعض التحيز. يوضح هذا المثال التنظيم البسيط المستخدم في\nمقدرات :ref:`shrunk_covariance`. على وجه الخصوص، يركز على كيفية\nتعيين مقدار التنظيم، أي كيفية اختيار المفاضلة بين التحيز والتباين.\n'

إنشاء بيانات عينة

n_features, n_samples = 40, 20
np.random.seed(42)
base_X_train = np.random.normal(size=(n_samples, n_features))
base_X_test = np.random.normal(size=(n_samples, n_features))

# تلوين العينات
coloring_matrix = np.random.normal(size=(n_features, n_features))
X_train = np.dot(base_X_train, coloring_matrix)
X_test = np.dot(base_X_test, coloring_matrix)

حساب الاحتمال على بيانات الاختبار

# تغطية نطاق من قيم معامل الانكماش المحتملة
shrinkages = np.logspace(-2, 0, 30)
negative_logliks = [
    -ShrunkCovariance(shrinkage=s).fit(X_train).score(X_test) for s in shrinkages
]

# تحت نموذج الحقيقة الأساسية، الذي لن نتمكن من الوصول إليه في الإعدادات الحقيقية
real_cov = np.dot(coloring_matrix.T, coloring_matrix)
emp_cov = empirical_covariance(X_train)
loglik_real = -log_likelihood(emp_cov, linalg.inv(real_cov))

مقارنة طرق مختلفة لتعيين معلمة التنظيم

هنا نقارن 3 طرق:

• تعيين المعلمة عن طريق التحقق المتبادل للاحتمال على ثلاث طيات وفقًا لشبكة من معلمات الانكماش المحتملة.

• صيغة مقفلة مقترحة من قبل Ledoit و Wolf لحساب معلمة التنظيم المثلى بشكل مقارب (تقليل معيار MSE )، مما ينتج عنه تقدير التغاير LedoitWolf.

• تحسين لانكماش Ledoit-Wolf، OAS، الذي اقترحه Chen et al. تقاربه أفضل بكثير بافتراض أن البيانات غاوسية، خاصة للعينات الصغيرة.

# GridSearch لمعامل انكماش مثالي
tuned_parameters = [{"shrinkage": shrinkages}]
cv = GridSearchCV(ShrunkCovariance(), tuned_parameters)
cv.fit(X_train)

# تقدير معامل الانكماش الأمثل لـ Ledoit-Wolf
lw = LedoitWolf()
loglik_lw = lw.fit(X_train).score(X_test)

# تقدير معامل OAS
oa = OAS()
loglik_oa = oa.fit(X_train).score(X_test)

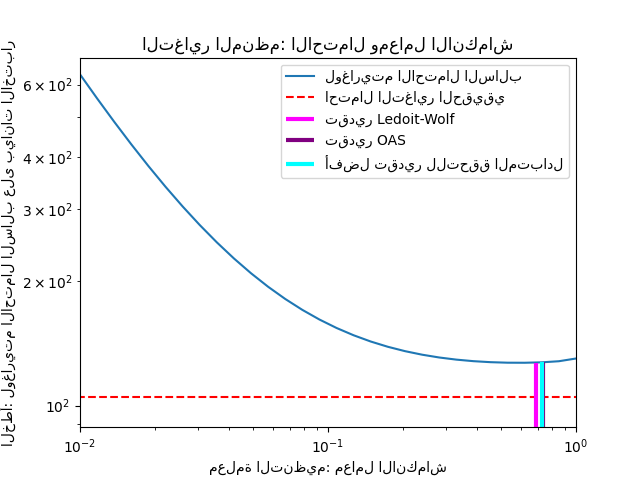
رسم النتائج

لتحديد خطأ التقدير كميًا، نرسم احتمال البيانات غير المرئية لـ قيم مختلفة لمعلمة الانكماش. نعرض أيضًا الخيارات بواسطة التحقق المتبادل، أو مع تقديرات LedoitWolf و OAS.

fig = plt.figure()
plt.title("التغاير المنظم: الاحتمال ومعامل الانكماش")
plt.xlabel("معلمة التنظيم: معامل الانكماش")
plt.ylabel("الخطأ: لوغاريتم الاحتمال السالب على بيانات الاختبار")
# نطاق منحنى الانكماش
plt.loglog(shrinkages, negative_logliks, label="لوغاريتم الاحتمال السالب")

plt.plot(plt.xlim(), 2 * [loglik_real], "--r", label="احتمال التغاير الحقيقي")

# ضبط العرض
lik_max = np.amax(negative_logliks)
lik_min = np.amin(negative_logliks)
ymin = lik_min - 6.0 * np.log((plt.ylim()[1] - plt.ylim()[0]))
ymax = lik_max + 10.0 * np.log(lik_max - lik_min)
xmin = shrinkages[0]
xmax = shrinkages[-1]
# احتمال LW
plt.vlines(
    lw.shrinkage_,
    ymin,
    -loglik_lw,
    color="magenta",
    linewidth=3,
    label="تقدير Ledoit-Wolf",
)
# احتمال OAS
plt.vlines(
    oa.shrinkage_, ymin, -loglik_oa, color="purple", linewidth=3, label="تقدير OAS"
)
# أفضل احتمال لمقدر CV
plt.vlines(
    cv.best_estimator_.shrinkage,
    ymin,
    -cv.best_estimator_.score(X_test),
    color="cyan",
    linewidth=3,
    label="أفضل تقدير للتحقق المتبادل",
)

plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.legend()

plt.show()

ملاحظة

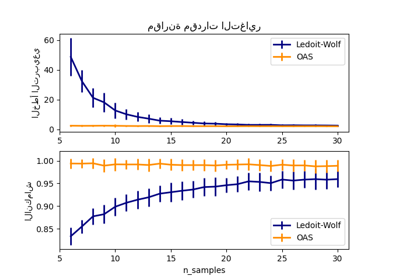
يتوافق تقدير أقصى احتمال مع عدم الانكماش، وبالتالي يكون أداؤه ضعيفًا. يعمل تقدير Ledoit-Wolf بشكل جيد حقًا، حيث إنه قريب من الأمثل وليس مكلفًا من الناحية الحسابية. في هذا المثال، يكون تقدير OAS بعيدًا بعض الشيء. ومن المثير للاهتمام، أن كلا النهجين يتفوقان على التحقق المتبادل، وهو الأكثر تكلفة من الناحية الحسابية.

Related examples

تأثير تحويل الأهداف في نموذج الانحدار

تأثير تحويل الأهداف في نموذج الانحدار

الانحدار الأيزوتوني

الانحدار الأيزوتوني

ربط الأنابيب: ربط PCA والانحدار اللوجستي

ربط الأنابيب: ربط PCA والانحدار اللوجستي

تقدير Ledoit-Wolf مقابل OAS

تقدير Ledoit-Wolf مقابل OAS