ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
نموذج الإهليجيات لمزيج غاوسي#
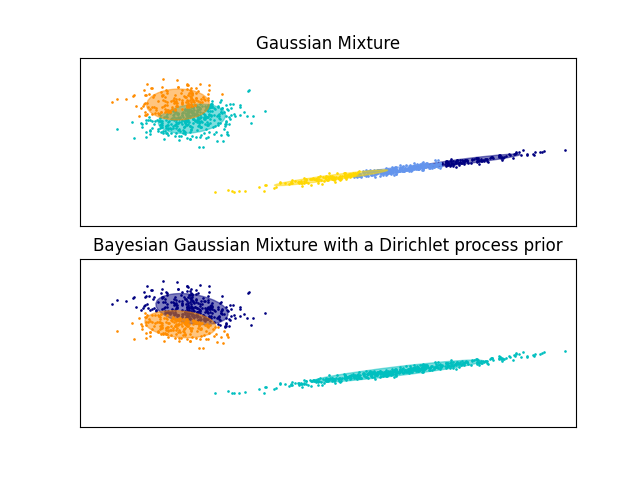
ارسم إهليجيات الثقة لمزيج من غاوسيين تم الحصول عليهما باستخدام التوقعات القصوى (فئة "GaussianMixture") والاستدلال المتغير (نماذج فئة "BayesianGaussianMixture" مع أولوية عملية ديريشليت).
لدى كلا النموذجين إمكانية الوصول إلى خمسة مكونات لملاءمة البيانات. لاحظ أن نموذج التوقعات القصوى سيستخدم بالضرورة جميع المكونات الخمسة بينما سيستخدم نموذج الاستدلال المتغير بشكل فعال فقط العديد من المكونات كما هو مطلوب للحصول على ملاءمة جيدة. هنا يمكننا أن نرى أن نموذج التوقعات القصوى يقسم بعض المكونات بشكل تعسفي، لأنه يحاول ملاءمة الكثير من المكونات، بينما يقوم نموذج عملية ديريشليت بتكييفه عدد الحالات تلقائيًا.
هذا المثال لا يظهر ذلك، لأننا في مساحة ذات أبعاد منخفضة، ولكن ميزة أخرى لنموذج عملية ديريشليت هي أنه يمكنه ملاءمة مصفوفات التغاير الكاملة بشكل فعال حتى عندما يكون هناك أقل أمثلة لكل مجموعة من الأبعاد في البيانات، وذلك بسبب خصائص التنظيم الخاصة بخوارزمية الاستدلال.
/project/workspace/sklearn/mixture/_base.py:269: ConvergenceWarning:
Best performing initialization did not converge. Try different init parameters, or increase max_iter, tol, or check for degenerate data.
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
import itertools
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg
from sklearn import mixture
color_iter = itertools.cycle(["navy", "c", "cornflowerblue", "gold", "darkorange"])
def plot_results(X, Y_, means, covariances, index, title):
splot = plt.subplot(2, 1, 1 + index)
for i, (mean, covar, color) in enumerate(zip(means, covariances, color_iter)):
v, w = linalg.eigh(covar)
v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# كما أن DP لن يستخدم كل مكون يمكنه الوصول إليه
# ما لم تكن هناك حاجة إليه، لا يجب علينا رسم المكونات الزائدة.
if not np.any(Y_ == i):
continue
plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], 0.8, color=color)
# ارسم إهليج لتوضيح المكون الغاوسي
angle = np.arctan(u[1] / u[0])
angle = 180.0 * angle / np.pi # تحويل إلى درجات
ell = mpl.patches.Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.5)
splot.add_artist(ell)
plt.xlim(-9.0, 5.0)
plt.ylim(-3.0, 6.0)
plt.xticks(())
plt.yticks(())
plt.title(title)
# عدد العينات لكل مكون
n_samples = 500
# توليد عينة عشوائية، مكونين
np.random.seed(0)
C = np.array([[0.0, -0.1], [1.7, 0.4]])
X = np.r_[
np.dot(np.random.randn(n_samples, 2), C),
0.7 * np.random.randn(n_samples, 2) + np.array([-6, 3]),
]
# ملاءمة مزيج غاوسي باستخدام التوقعات القصوى بخمسة مكونات
gmm = mixture.GaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0, "Gaussian Mixture")
# ملاءمة مزيج غاوسي لعملية ديريشليت باستخدام خمسة مكونات
dpgmm = mixture.BayesianGaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(
X,
dpgmm.predict(X),
dpgmm.means_,
dpgmm.covariances_,
1,
"Bayesian Gaussian Mixture with a Dirichlet process prior",
)
plt.show()
Total running time of the script: (0 minutes 0.405 seconds)
Related examples
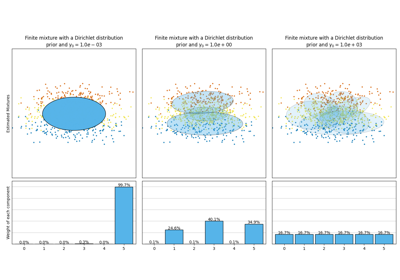
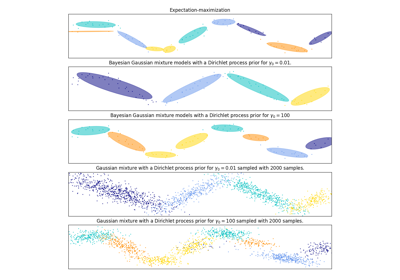
تحليل نوع أولوية التركيز لخوارزمية التباين بايزي غاوسي ميكسشر