ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

تحليل نوع أولوية التركيز لخوارزمية التباين بايزي غاوسي ميكسشر#

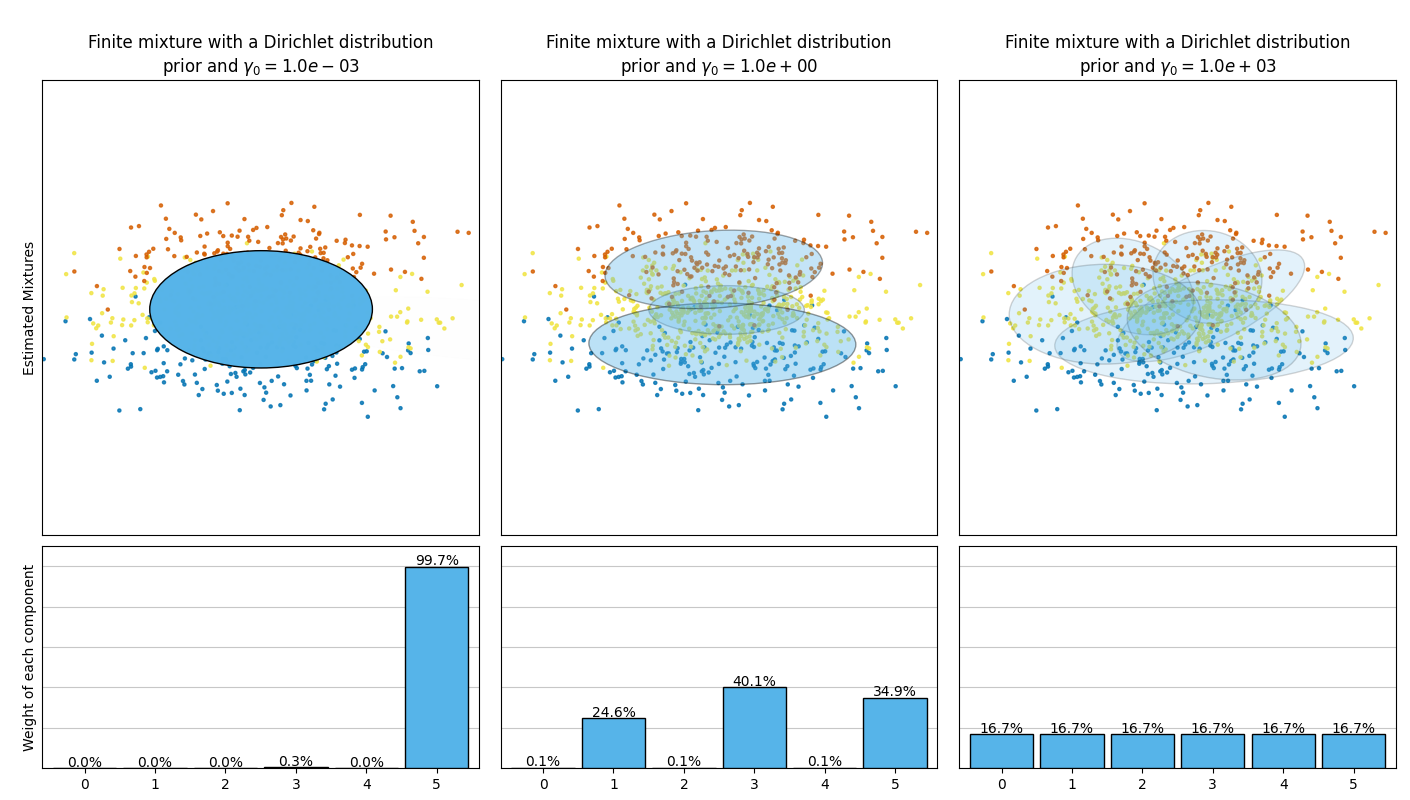
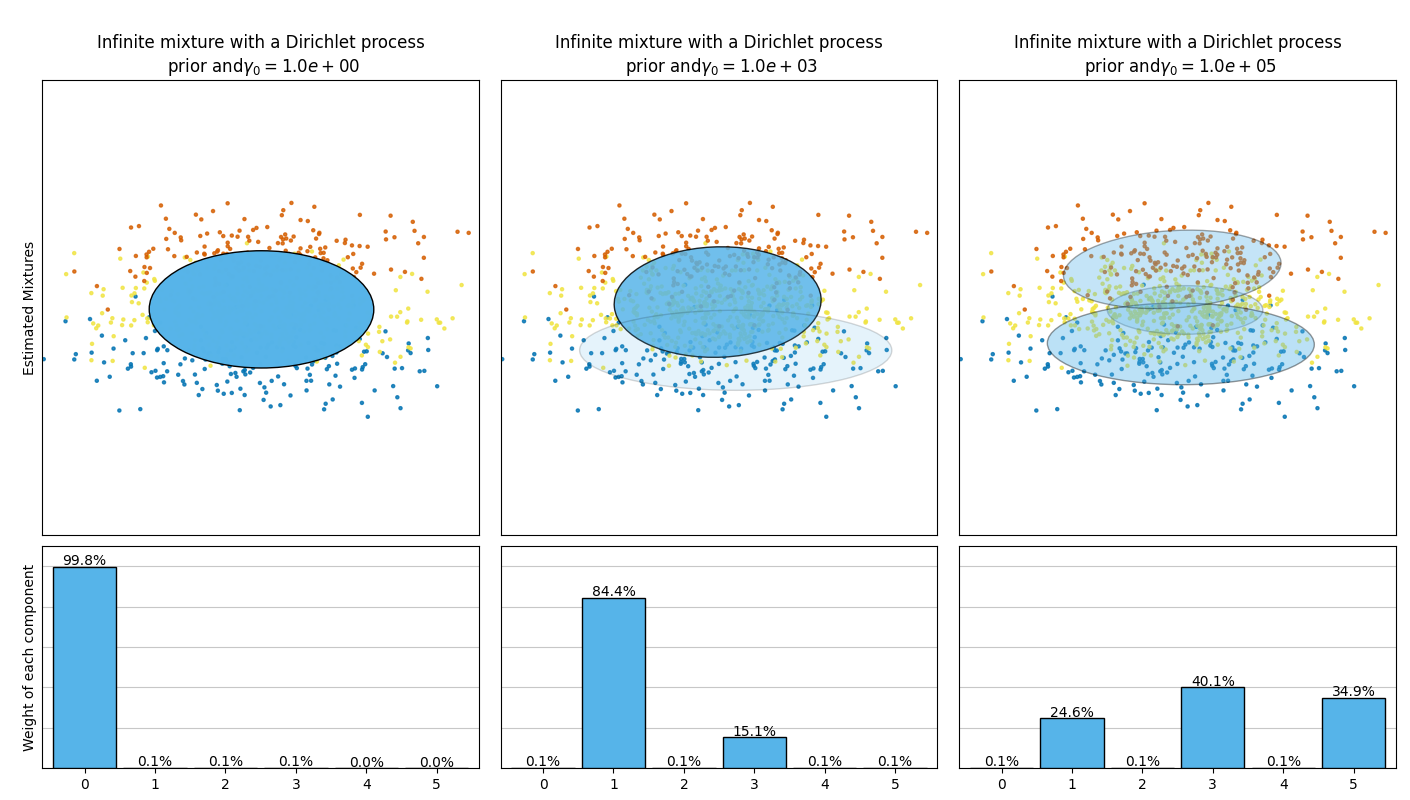
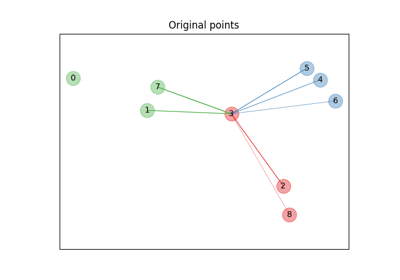
هذا المثال يقوم برسم الإهليبسيد (ellipsoids) المستخلصة من مجموعة بيانات تجريبية (خليط من ثلاثة توزيعات غاوسية) باستخدام نماذج فئة "بايزي غاوسي ميكسشر" مع توزيع ديريشليت كأولوية (weight_concentration_prior_type='dirichlet_distribution') وأولوية عملية ديريشليت (weight_concentration_prior_type='dirichlet_process'). في كل شكل، نقوم برسم النتائج لثلاث قيم مختلفة لأولوية وزن التركيز.

يمكن لفئة "بايزي غاوسي ميكسشر" أن تكيف عدد مكونات المزيج تلقائياً. للبارامتر "weight_concentration_prior" ارتباط مباشر مع العدد الناتج للمكونات ذات الأوزان غير الصفرية. تحديد قيمة منخفضة للأولوية المركزية سيجعل النموذج يضع معظم الوزن على مكونات قليلة، ويحدد أوزان المكونات المتبقية قريبة جداً من الصفر. القيم العالية للأولوية المركزية ستسمح لعدد أكبر من المكونات أن تكون نشطة في المزيج.

تسمح أولوية عملية ديريشليت بتعريف عدد لانهائي من المكونات وتختار تلقائياً العدد الصحيح من المكونات: تنشط مكوناً فقط إذا كان ذلك ضرورياً.

على العكس، فإن نموذج المزيج المحدود الكلاسيكي مع أولوية توزيع ديريشليت سيفضل مكونات موزونة بشكل أكثر توازناً وبالتالي يميل إلى تقسيم التجمعات الطبيعية إلى مكونات فرعية غير ضرورية.

$Finite mixture with a Dirichlet distribution prior and $\gamma_0=$$1.0e-03$, Finite mixture with a Dirichlet distribution prior and $\gamma_0=$$1.0e+00$, Finite mixture with a Dirichlet distribution prior and $\gamma_0=$$1.0e+03$$
$Infinite mixture with a Dirichlet process prior and$\gamma_0=$$1.0e+00$, Infinite mixture with a Dirichlet process prior and$\gamma_0=$$1.0e+03$, Infinite mixture with a Dirichlet process prior and$\gamma_0=$$1.0e+05$$

# المؤلفون: مطوري سكايلرن
# تعريف الترخيص: BSD-3-Clause

import matplotlib as mpl
import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import numpy as np

from sklearn.mixture import BayesianGaussianMixture


def plot_ellipses(ax, weights, means, covars):
    for n in range(means.shape[0]):
        eig_vals, eig_vecs = np.linalg.eigh(covars[n])
        unit_eig_vec = eig_vecs[0] / np.linalg.norm(eig_vecs[0])
        angle = np.arctan2(unit_eig_vec[1], unit_eig_vec[0])
        # Ellipse needs degrees
        angle = 180 * angle / np.pi
        # eigenvector normalization
        eig_vals = 2 * np.sqrt(2) * np.sqrt(eig_vals)
        ell = mpl.patches.Ellipse(
            means[n], eig_vals[0], eig_vals[1], angle=180 + angle, edgecolor="black"
        )
        ell.set_clip_box(ax.bbox)
        ell.set_alpha(weights[n])
        ell.set_facecolor("#56B4E9")
        ax.add_artist(ell)


def plot_results(ax1, ax2, estimator, X, y, title, plot_title=False):
    ax1.set_title(title)
    ax1.scatter(X[:, 0], X[:, 1], s=5, marker="o", color=colors[y], alpha=0.8)
    ax1.set_xlim(-2.0, 2.0)
    ax1.set_ylim(-3.0, 3.0)
    ax1.set_xticks(())
    ax1.set_yticks(())
    plot_ellipses(ax1, estimator.weights_, estimator.means_, estimator.covariances_)

    ax2.get_xaxis().set_tick_params(direction="out")
    ax2.yaxis.grid(True, alpha=0.7)
    for k, w in enumerate(estimator.weights_):
        ax2.bar(
            k,
            w,
            width=0.9,
            color="#56B4E9",
            zorder=3,
            align="center",
            edgecolor="black",
        )
        ax2.text(k, w + 0.007, "%.1f%%" % (w * 100.0), horizontalalignment="center")
    ax2.set_xlim(-0.6, 2 * n_components - 0.4)
    ax2.set_ylim(0.0, 1.1)
    ax2.tick_params(axis="y", which="both", left=False, right=False, labelleft=False)
    ax2.tick_params(axis="x", which="both", top=False)

    if plot_title:
        ax1.set_ylabel("Estimated Mixtures")
        ax2.set_ylabel("Weight of each component")


# بارامترات مجموعة البيانات
random_state, n_components, n_features = 2, 3, 2
colors = np.array(["#0072B2", "#F0E442", "#D55E00"])

covars = np.array(
    [[[0.7, 0.0], [0.0, 0.1]], [[0.5, 0.0], [0.0, 0.1]], [[0.5, 0.0], [0.0, 0.1]]]
)
samples = np.array([200, 500, 200])
means = np.array([[0.0, -0.70], [0.0, 0.0], [0.0, 0.70]])

# mean_precision_prior= 0.8 لتقليل تأثير الأولوية
estimators = [
    (
        "Finite mixture with a Dirichlet distribution\nprior and " r"$\gamma_0=$",
        BayesianGaussianMixture(
            weight_concentration_prior_type="dirichlet_distribution",
            n_components=2 * n_components,
            reg_covar=0,
            init_params="random",
            max_iter=1500,
            mean_precision_prior=0.8,
            random_state=random_state,
        ),
        [0.001, 1, 1000],
    ),
    (
        "Infinite mixture with a Dirichlet process\n prior and" r"$\gamma_0=$",
        BayesianGaussianMixture(
            weight_concentration_prior_type="dirichlet_process",
            n_components=2 * n_components,
            reg_covar=0,
            init_params="random",
            max_iter=1500,
            mean_precision_prior=0.8,
            random_state=random_state,
        ),
        [1, 1000, 100000],
    ),
]

# توليد البيانات
rng = np.random.RandomState(random_state)
X = np.vstack(
    [
        rng.multivariate_normal(means[j], covars[j], samples[j])
        for j in range(n_components)
    ]
)

y = np.concatenate([np.full(samples[j], j, dtype=int) for j in range(n_components)])


# رسم النتائج في شكلين مختلفين
for title, estimator, concentrations_prior in estimators:
    plt.figure(figsize=(4.7 * 3, 8))
    plt.subplots_adjust(
        bottom=0.04, top=0.90, hspace=0.05, wspace=0.05, left=0.03, right=0.99
    )

    gs = gridspec.GridSpec(3, len(concentrations_prior))
    for k, concentration in enumerate(concentrations_prior):
        estimator.weight_concentration_prior = concentration
        estimator.fit(X)
        plot_results(
            plt.subplot(gs[0:2, k]),
            plt.subplot(gs[2, k]),
            estimator,
            X,
            y,
            r"%s$%.1e$" % (title, concentration),
            plot_title=k == 0,
        )

plt.show()