ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
تشتتات GMM#
توضيح لعدة أنواع من التشتتات لمزيج النماذج الغاوسية.
راجع نماذج خليط غاوسي للمزيد من المعلومات حول المحلل.
على الرغم من أن GMM تستخدم غالبًا للتجمع، يمكننا مقارنة التجمعات التي تم الحصول عليها مع الفئات الفعلية من مجموعة البيانات. نقوم بتهيئة المتوسطات لغاوسيات مع متوسطات الفئات من مجموعة التدريب لجعل هذه المقارنة صالحة.
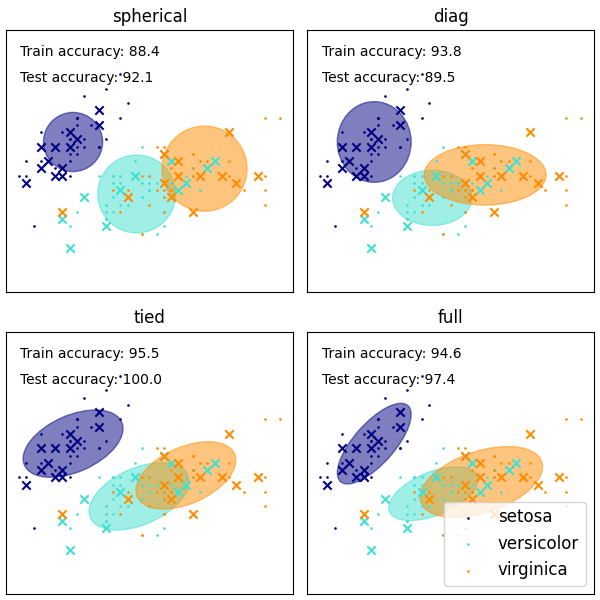
نحن نرسم العلامات المتوقعة على كل من بيانات التدريب والاختبار المحجوزة باستخدام مجموعة متنوعة من أنواع تشتت GMM على مجموعة بيانات الزهرة. نقارن بين GMMs مع كروية، قطري، كامل، ومتصل مصفوفات التشتت بترتيب تصاعدي للأداء. على الرغم من أن المرء يتوقع أن يعمل التشتت الكامل بشكل أفضل بشكل عام، إلا أنه عرضة للإفراط في التكيف على مجموعات البيانات الصغيرة ولا يعمم جيدًا على بيانات الاختبار المحجوزة.
في الرسوم البيانية، يتم عرض بيانات التدريب على شكل نقاط، بينما يتم عرض بيانات الاختبار على شكل صلبان. مجموعة بيانات الزهرة ذات أربعة أبعاد. يتم عرض البعدين الأولين فقط هنا، وبالتالي يتم فصل بعض النقاط في أبعاد أخرى.
# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import StratifiedKFold
colors = ["navy", "turquoise", "darkorange"]
def make_ellipses(gmm, ax):
for n, color in enumerate(colors):
if gmm.covariance_type == "full":
covariances = gmm.covariances_[n][:2, :2]
elif gmm.covariance_type == "tied":
covariances = gmm.covariances_[:2, :2]
elif gmm.covariance_type == "diag":
covariances = np.diag(gmm.covariances_[n][:2])
elif gmm.covariance_type == "spherical":
covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]
v, w = np.linalg.eigh(covariances)
u = w[0] / np.linalg.norm(w[0])
angle = np.arctan2(u[1], u[0])
angle = 180 * angle / np.pi # تحويل إلى درجات
v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
ell = mpl.patches.Ellipse(
gmm.means_[n, :2], v[0], v[1], angle=180 + angle, color=color
)
ell.set_clip_box(ax.bbox)
ell.set_alpha(0.5)
ax.add_artist(ell)
ax.set_aspect("equal", "datalim")
iris = datasets.load_iris()
# قم بتقسيم مجموعة البيانات إلى مجموعات تدريب (75%) واختبار (25%)
# مجموعات غير متداخلة.
skf = StratifiedKFold(n_splits=4)
# خذ فقط الطية الأولى.
train_index, test_index = next(iter(skf.split(iris.data, iris.target)))
X_train = iris.data[train_index]
y_train = iris.target[train_index]
X_test = iris.data[test_index]
y_test = iris.target[test_index]
n_classes = len(np.unique(y_train))
# جرب GMMs باستخدام أنواع مختلفة من التشتتات.
estimators = {
cov_type: GaussianMixture(
n_components=n_classes, covariance_type=cov_type, max_iter=20, random_state=0
)
for cov_type in ["spherical", "diag", "tied", "full"]
}
n_estimators = len(estimators)
plt.figure(figsize=(3 * n_estimators // 2, 6))
plt.subplots_adjust(
bottom=0.01, top=0.95, hspace=0.15, wspace=0.05, left=0.01, right=0.99
)
for index, (name, estimator) in enumerate(estimators.items()):
# نظرًا لأن لدينا تسميات الفئات لبيانات التدريب، يمكننا
# تهيئة معلمات GMM بطريقة خاضعة للإشراف.
estimator.means_init = np.array(
[X_train[y_train == i].mean(axis=0) for i in range(n_classes)]
)
# تدريب المعلمات الأخرى باستخدام خوارزمية EM.
estimator.fit(X_train)
h = plt.subplot(2, n_estimators // 2, index + 1)
make_ellipses(estimator, h)
for n, color in enumerate(colors):
data = iris.data[iris.target == n]
plt.scatter(
data[:, 0], data[:, 1], s=0.8, color=color, label=iris.target_names[n]
)
# رسم بيانات الاختبار بعلامات الصليب
for n, color in enumerate(colors):
data = X_test[y_test == n]
plt.scatter(data[:, 0], data[:, 1], marker="x", color=color)
y_train_pred = estimator.predict(X_train)
train_accuracy = np.mean(y_train_pred.ravel() == y_train.ravel()) * 100
plt.text(0.05, 0.9, "Train accuracy: %.1f" % train_accuracy, transform=h.transAxes)
y_test_pred = estimator.predict(X_test)
test_accuracy = np.mean(y_test_pred.ravel() == y_test.ravel()) * 100
plt.text(0.05, 0.8, "Test accuracy: %.1f" % test_accuracy, transform=h.transAxes)
plt.xticks(())
plt.yticks(())
plt.title(name)
plt.legend(scatterpoints=1, loc="lower right", prop=dict(size=12))
plt.show()
Total running time of the script: (0 minutes 0.290 seconds)
Related examples
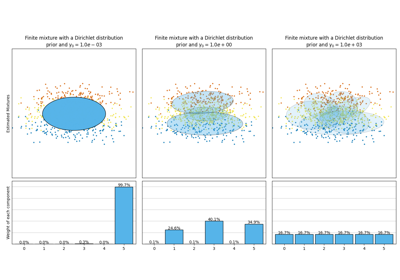
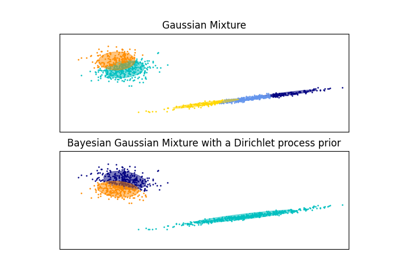
تحليل نوع أولوية التركيز لخوارزمية التباين بايزي غاوسي ميكسشر