ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
نموذج مزيج غاوسي لمنحنى الجيب#
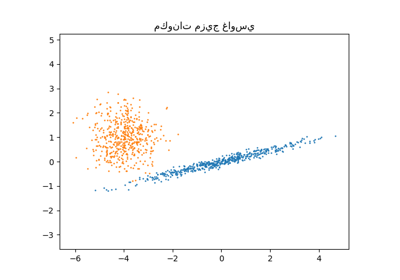
هذا المثال يوضح سلوك نماذج المزيج الغاوسي التي تم ضبطها على بيانات لم يتم أخذ عينات منها من متغيرات غاوسية عشوائية. مجموعة البيانات تتكون من 100 نقطة متباعدة بشكل فضفاض تتبع منحنى جيب متعرج. لذلك لا يوجد قيمة حقيقية لعدد المكونات الغاوسية.
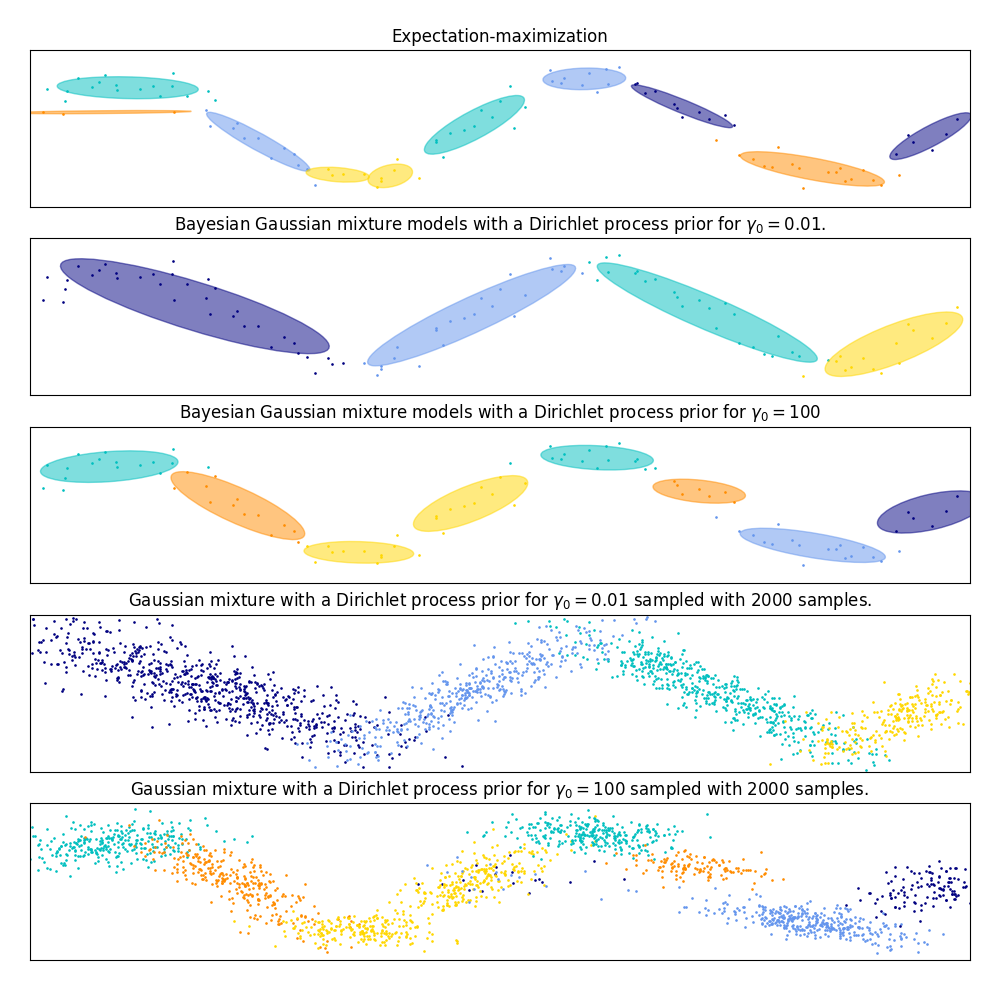
النموذج الأول هو نموذج مزيج غاوسي كلاسيكي بـ 10 مكونات تم ضبطه باستخدام خوارزمية التوقع-التعظيم.
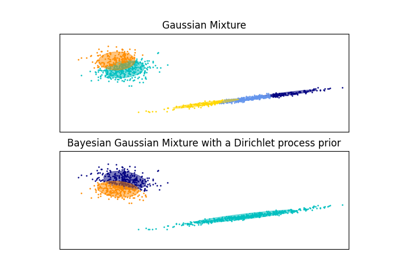
النموذج الثاني هو نموذج مزيج غاوسي بايزي مع عملية ديريشليت كأولوية تم ضبطها باستخدام الاستدلال المتغير. القيمة المنخفضة للأولوية التركيز تجعل النموذج يفضل عددًا أقل من المكونات النشطة. هذه النماذج "تقرر" أن تركز قوتها في النمذجة على الصورة الكبيرة لهيكل مجموعة البيانات: مجموعات من النقاط ذات الاتجاهات المتناوبة التي تم نمذجتها بواسطة مصفوفات التباين غير القطري. هذه الاتجاهات المتناوبة تلتقط بشكل تقريبي الطبيعة المتناوبة للإشارة الجيبية الأصلية.
النموذج الثالث هو أيضًا نموذج مزيج غاوسي بايزي مع عملية ديريشليت كأولوية ولكن هذه المرة تكون قيمة أولوية التركيز أعلى مما يعطي النموذج حرية أكبر لنمذجة البنية الدقيقة للبيانات. النتيجة هي مزيج بعدد أكبر من المكونات النشطة مشابه للنموذج الأول حيث قررنا بشكل تعسفي تثبيت عدد المكونات إلى 10.
أي نموذج هو الأفضل هو مسألة حكم ذاتي: هل نريد تفضيل النماذج التي تلتقط فقط الصورة الكبيرة لتلخيص وتفسير معظم بنية البيانات مع تجاهل التفاصيل أم أننا نفضل النماذج التي تتبع عن كثب المناطق عالية الكثافة للإشارة؟
يظهر اللوحان الأخيران كيف يمكننا أخذ عينات من النموذجين الأخيرين. توزيعات العينات الناتجة لا تبدو تمامًا مثل توزيع البيانات الأصلية. ينبع الفرق في المقام الأول من خطأ التقريب الذي قمنا به باستخدام نموذج يفترض أن البيانات تم إنشاؤها بواسطة عدد محدود من المكونات الغاوسية بدلاً من منحنى جيب متعرج مستمر.
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
import itertools
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg
from sklearn import mixture
color_iter = itertools.cycle(["navy", "c", "cornflowerblue", "gold", "darkorange"])
def plot_results(X, Y, means, covariances, index, title):
splot = plt.subplot(5, 1, 1 + index)
for i, (mean, covar, color) in enumerate(zip(means, covariances, color_iter)):
v, w = linalg.eigh(covar)
v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# كما أن DP لن يستخدم كل مكون لديه حق الوصول إليه
# إلا إذا كان بحاجة إليه، لا يجب أن نرسم المكونات الزائدة.
if not np.any(Y == i):
continue
plt.scatter(X[Y == i, 0], X[Y == i, 1], 0.8, color=color)
# ارسم بيضاوي لإظهار المكون الغاوسي
angle = np.arctan(u[1] / u[0])
angle = 180.0 * angle / np.pi # تحويل إلى درجات
ell = mpl.patches.Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.5)
splot.add_artist(ell)
plt.xlim(-6.0, 4.0 * np.pi - 6.0)
plt.ylim(-5.0, 5.0)
plt.title(title)
plt.xticks(())
plt.yticks(())
def plot_samples(X, Y, n_components, index, title):
plt.subplot(5, 1, 4 + index)
for i, color in zip(range(n_components), color_iter):
# كما أن DP لن يستخدم كل مكون لديه حق الوصول إليه
# إلا إذا كان بحاجة إليه، لا يجب أن نرسم المكونات الزائدة.
if not np.any(Y == i):
continue
plt.scatter(X[Y == i, 0], X[Y == i, 1], 0.8, color=color)
plt.xlim(-6.0, 4.0 * np.pi - 6.0)
plt.ylim(-5.0, 5.0)
plt.title(title)
plt.xticks(())
plt.yticks(())
# المعاملات
n_samples = 100
# توليد عينة عشوائية تتبع منحنى جيب
np.random.seed(0)
X = np.zeros((n_samples, 2))
step = 4.0 * np.pi / n_samples
for i in range(X.shape[0]):
x = i * step - 6.0
X[i, 0] = x + np.random.normal(0, 0.1)
X[i, 1] = 3.0 * (np.sin(x) + np.random.normal(0, 0.2))
plt.figure(figsize=(10, 10))
plt.subplots_adjust(
bottom=0.04, top=0.95, hspace=0.2, wspace=0.05, left=0.03, right=0.97
)
# ضبط مزيج غاوسي باستخدام خوارزمية التوقع-التعظيم بعشرة مكونات
gmm = mixture.GaussianMixture(
n_components=10, covariance_type="full", max_iter=100
).fit(X)
plot_results(
X, gmm.predict(X), gmm.means_, gmm.covariances_, 0, "Expectation-maximization"
)
dpgmm = mixture.BayesianGaussianMixture(
n_components=10,
covariance_type="full",
weight_concentration_prior=1e-2,
weight_concentration_prior_type="dirichlet_process",
mean_precision_prior=1e-2,
covariance_prior=1e0 * np.eye(2),
init_params="random",
max_iter=100,
random_state=2,
).fit(X)
plot_results(
X,
dpgmm.predict(X),
dpgmm.means_,
dpgmm.covariances_,
1,
"Bayesian Gaussian mixture models with a Dirichlet process prior "
r"for $\gamma_0=0.01$.",
)
X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(
X_s,
y_s,
dpgmm.n_components,
0,
"Gaussian mixture with a Dirichlet process prior "
r"for $\gamma_0=0.01$ sampled with $2000$ samples.",
)
dpgmm = mixture.BayesianGaussianMixture(
n_components=10,
covariance_type="full",
weight_concentration_prior=1e2,
weight_concentration_prior_type="dirichlet_process",
mean_precision_prior=1e-2,
covariance_prior=1e0 * np.eye(2),
init_params="kmeans",
max_iter=100,
random_state=2,
).fit(X)
plot_results(
X,
dpgmm.predict(X),
dpgmm.means_,
dpgmm.covariances_,
2,
"Bayesian Gaussian mixture models with a Dirichlet process prior "
r"for $\gamma_0=100$",
)
X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(
X_s,
y_s,
dpgmm.n_components,
1,
"Gaussian mixture with a Dirichlet process prior "
r"for $\gamma_0=100$ sampled with $2000$ samples.",
)
plt.show()
Total running time of the script: (0 minutes 0.521 seconds)
Related examples
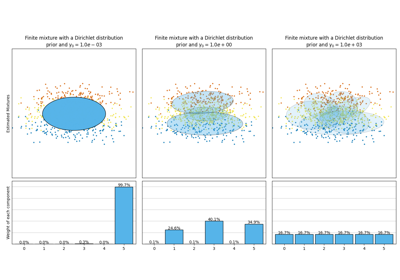
تحليل نوع أولوية التركيز لخوارزمية التباين بايزي غاوسي ميكسشر