ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

طرق تهيئة نماذج الخلط الغاوسي#

أمثلة على الطرق المختلفة للتهيئة في نماذج الخلط الغاوسي

راجع نماذج خليط غاوسي لمزيد من المعلومات حول المحلل.

هنا نقوم بتوليد بعض بيانات العينة مع أربع مجموعات سهلة التحديد. الغرض من هذا المثال هو إظهار الطرق الأربع المختلفة لمعلمة التهيئة init_param.

التهيئات الأربعة هي kmeans (الافتراضي)، random، random_from_data و k-means++.

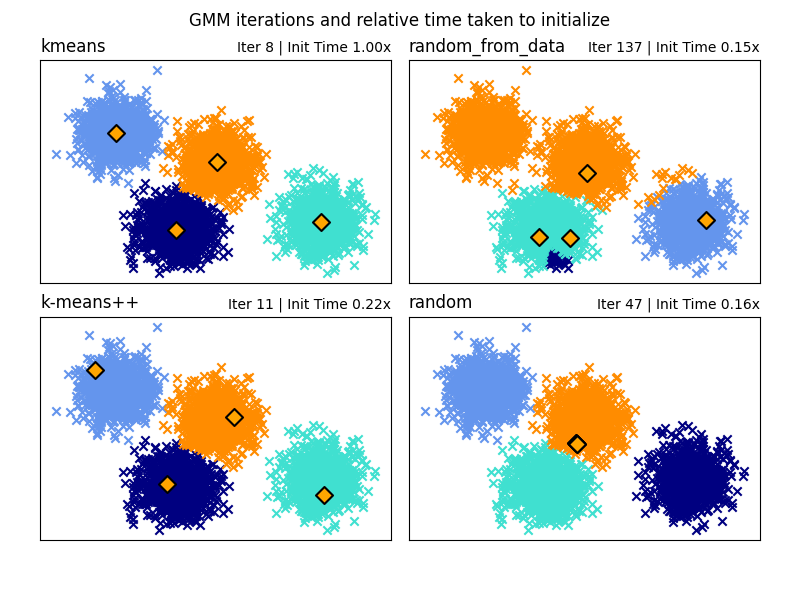
تمثل الماسات البرتقالية مراكز التهيئة للنماذج الغاوسية التي تم إنشاؤها بواسطة init_param. يتم تمثيل بقية البيانات على شكل صلبان وتمثل الألوان التصنيف المرتبط النهائي بعد انتهاء النموذج الغاوسي.

تمثل الأرقام في الزاوية العلوية اليمنى من كل رسم فرعي عدد التكرارات التي تم اتخاذها لتقارب GaussianMixture والوقت النسبي الذي استغرقته عملية التهيئة لجزء الخوارزمية. تميل أوقات التهيئة الأقصر إلى وجود عدد أكبر من التكرارات للتقارب.

وقت التهيئة هو نسبة الوقت المستغرق لتلك الطريقة مقابل الوقت المستغرق لطريقة kmeans الافتراضية. كما ترى، تستغرق جميع الطرق البديلة الثلاثة وقتًا أقل للتهيئة عند مقارنتها بـ kmeans.

في هذا المثال، عند تهيئة النموذج باستخدام random_from_data أو random، يستغرق النموذج مزيدًا من التكرارات للتقارب. هنا، يقوم k-means++ بعمل جيد لكل من الوقت المنخفض للتهيئة وعدد تكرارات GaussianMixture المنخفضة للتقارب.

GMM iterations and relative time taken to initialize, kmeans, Iter 8 | Init Time 1.00x, random_from_data, Iter 137 | Init Time 0.15x, k-means++, Iter 11 | Init Time 0.22x, random, Iter 47 | Init Time 0.16x

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

from timeit import default_timer as timer

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets._samples_generator import make_blobs
from sklearn.mixture import GaussianMixture
from sklearn.utils.extmath import row_norms

print(__doc__)

# توليد بعض البيانات

X, y_true = make_blobs(n_samples=4000, centers=4, cluster_std=0.60, random_state=0)
X = X[:, ::-1]

n_samples = 4000
n_components = 4
x_squared_norms = row_norms(X, squared=True)


def get_initial_means(X, init_params, r):
    # تشغيل GaussianMixture مع max_iter=0 لإخراج متوسطات التهيئة
    gmm = GaussianMixture(
        n_components=4, init_params=init_params, tol=1e-9, max_iter=0, random_state=r
    ).fit(X)
    return gmm.means_


methods = ["kmeans", "random_from_data", "k-means++", "random"]
colors = ["navy", "turquoise", "cornflowerblue", "darkorange"]
times_init = {}
relative_times = {}

plt.figure(figsize=(4 * len(methods) // 2, 6))
plt.subplots_adjust(
    bottom=0.1, top=0.9, hspace=0.15, wspace=0.05, left=0.05, right=0.95
)

for n, method in enumerate(methods):
    r = np.random.RandomState(seed=1234)
    plt.subplot(2, len(methods) // 2, n + 1)

    start = timer()
    ini = get_initial_means(X, method, r)
    end = timer()
    init_time = end - start

    gmm = GaussianMixture(
        n_components=4, means_init=ini, tol=1e-9, max_iter=2000, random_state=r
    ).fit(X)

    times_init[method] = init_time
    for i, color in enumerate(colors):
        data = X[gmm.predict(X) == i]
        plt.scatter(data[:, 0], data[:, 1], color=color, marker="x")

    plt.scatter(
        ini[:, 0], ini[:, 1], s=75, marker="D", c="orange", lw=1.5, edgecolors="black"
    )
    relative_times[method] = times_init[method] / times_init[methods[0]]

    plt.xticks(())
    plt.yticks(())
    plt.title(method, loc="left", fontsize=12)
    plt.title(
        "Iter %i | Init Time %.2fx" % (gmm.n_iter_, relative_times[method]),
        loc="right",
        fontsize=10,
    )
plt.suptitle("GMM iterations and relative time taken to initialize")
plt.show()