ضبط معامل الانتظام لخوارزمية SVC

يوضح المثال التالي تأثير ضبط معامل الانتظام عند استخدام آلات الدعم المتجهية (SVM) لتصنيف classification. بالنسبة لتصنيف SVC، نهتم بتصغير الخطر للمعادلة التالية:

\[C \sum_{i=1, n} \mathcal{L} (f(x_i), y_i) + \Omega (w)\]

حيث:

• \(C\) يستخدم لتحديد كمية الانتظام.

• \(\mathcal{L}\) هي دالة 'الخسارة' لعيناتنا ومعاملات نموذجنا.

• \(\Omega\) هي دالة 'العقوبة' لمعاملات نموذجنا.

إذا اعتبرنا دالة الخسارة هي الخطأ الفردي لكل عينة، فإن مصطلح ملاءمة البيانات، أو مجموع الخطأ لكل عينة، يزيد مع إضافة المزيد من العينات. ومع ذلك، فإن مصطلح العقوبة لا يزيد.

عند استخدام، على سبيل المثال، cross validation، لتحديد كمية الانتظام مع 'C'، سيكون هناك عدد مختلف من العينات بين المشكلة الرئيسية والمشاكل الأصغر داخل طيات التحقق المتقاطع.

بما أن دالة الخسارة تعتمد على عدد العينات، فإن ذلك يؤثر على القيمة المختارة لـ 'C'. والسؤال الذي يطرح نفسه هو "كيف يمكننا ضبط 'C' بشكل أمثل لمراعاة العدد المختلف من عينات التدريب؟"

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

توليد البيانات

في هذا المثال، نستكشف تأثير إعادة معلمة معامل الانتظام 'C' لمراعاة عدد العينات عند استخدام عقوبة L1 أو L2. لهذا الغرض، نقوم بإنشاء مجموعة بيانات اصطناعية ذات عدد كبير من الميزات، منها القليل فقط ذو دلالة. لذلك، نتوقع أن يؤدي الانتظام إلى تصغير المعاملات نحو الصفر (عقوبة L2) أو بالضبط إلى الصفر (عقوبة L1).

from sklearn.datasets import make_classification

n_samples, n_features = 100, 300
X, y = make_classification(
    n_samples=n_samples, n_features=n_features, n_informative=5, random_state=1
)

حالة عقوبة L1

في حالة L1، تقول النظرية إنه في حالة الانتظام القوي، لا يمكن للمقدر أن يتنبأ بنفس جودة نموذج يعرف التوزيع الحقيقي (حتى في حالة نمو حجم العينة إلى ما لا نهاية) حيث قد يحدد بعض أوزان الميزات التنبؤية إلى الصفر، مما يسبب انحياز. ومع ذلك، تقول النظرية إنه من الممكن إيجاد المجموعة الصحيحة من المعاملات غير الصفرية وكذلك إشاراتها عن طريق ضبط 'C'.

نحدد SVC الخطي بعقوبة L1.

from sklearn.svm import LinearSVC

model_l1 = LinearSVC(penalty="l1", loss="squared_hinge", dual=False, tol=1e-3)

نحسب متوسط درجة الاختبار لقيم مختلفة من 'C' عبر التحقق المتقاطع.

import numpy as np
import pandas as pd

from sklearn.model_selection import ShuffleSplit, validation_curve

Cs = np.logspace(-2.3, -1.3, 10)
train_sizes = np.linspace(0.3, 0.7, 3)
labels = [f"fraction: {train_size}" for train_size in train_sizes]
shuffle_params = {
    "test_size": 0.3,
    "n_splits": 150,
    "random_state": 1,
}

results = {"C": Cs}
for label, train_size in zip(labels, train_sizes):
    cv = ShuffleSplit(train_size=train_size, **shuffle_params)
    train_scores, test_scores = validation_curve(
        model_l1,
        X,
        y,
        param_name="C",
        param_range=Cs,
        cv=cv,
        n_jobs=2,
    )
    results[label] = test_scores.mean(axis=1)
results = pd.DataFrame(results)

import matplotlib.pyplot as plt

fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(12, 6))

# رسم النتائج بدون ضبط 'C'
results.plot(x="C", ax=axes[0], logx=True)
axes[0].set_ylabel("درجة التحقق المتقاطع")
axes[0].set_title("بدون ضبط")

for label in labels:
    best_C = results.loc[results[label].idxmax(), "C"]
    axes[0].axvline(x=best_C, linestyle="--", color="grey", alpha=0.7)

# رسم النتائج بضبط 'C'
for train_size_idx, label in enumerate(labels):
    train_size = train_sizes[train_size_idx]
    results_scaled = results[[label]].assign(
        C_scaled=Cs * float(n_samples * np.sqrt(train_size))
    )
    results_scaled.plot(x="C_scaled", ax=axes[1], logx=True, label=label)
    best_C_scaled = results_scaled["C_scaled"].loc[results[label].idxmax()]
    axes[1].axvline(x=best_C_scaled, linestyle="--", color="grey", alpha=0.7)

axes[1].set_title("ضبط 'C' بواسطة sqrt(1 / n_samples)")

_ = fig.suptitle("تأثير ضبط 'C' بعقوبة L1")

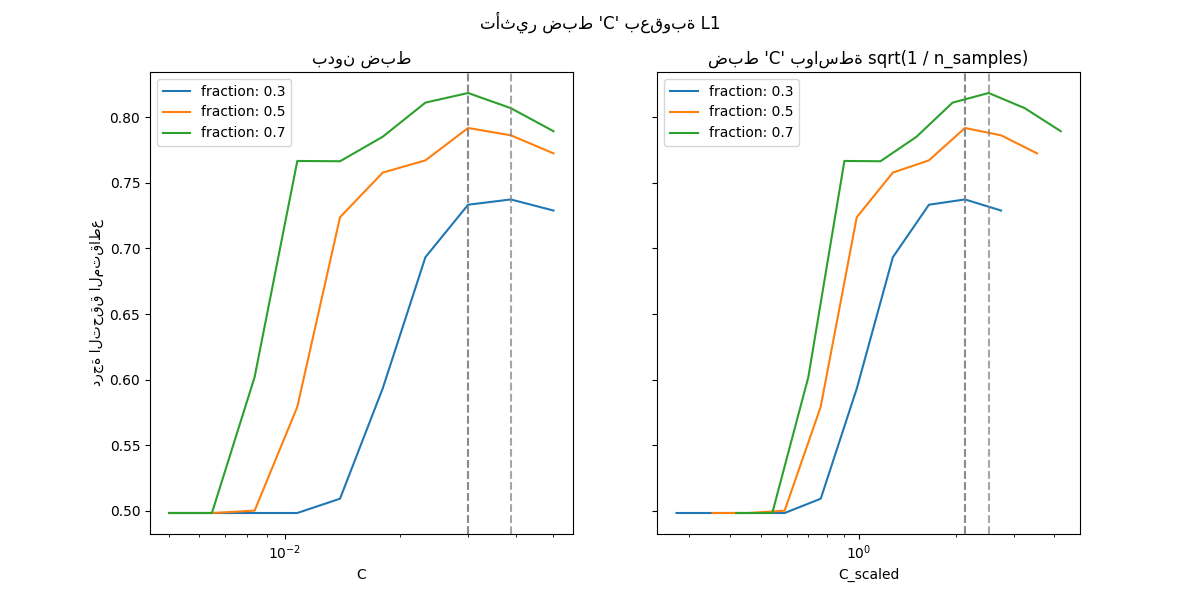
في منطقة 'C' الصغيرة (الانتظام القوي)، جميع المعاملات التي يتعلمها النموذج تساوي الصفر، مما يؤدي إلى نقص كبير في الملاءمة. بالفعل، الدقة في هذه المنطقة هي على مستوى الصدفة.

باستخدام المقياس الافتراضي يؤدي إلى قيمة مثلى مستقرة نوعا ما لـ 'C'، في حين أن الانتقال خارج منطقة نقص الملاءمة يعتمد على عدد عينات التدريب. تؤدي إعادة المعلمة إلى نتائج أكثر استقرارا.

انظر على سبيل المثال النظرية 3 من On the prediction performance of the Lasso أو Simultaneous analysis of Lasso and Dantzig selector حيث يفترض أن معامل الانتظام متناسب دائما مع 1 / sqrt(n_samples).

حالة عقوبة L2

يمكننا إجراء تجربة مماثلة مع عقوبة L2. في هذه الحالة، تقول النظرية إنه لتحقيق اتساق التنبؤ، يجب الحفاظ على معامل العقوبة ثابتا مع نمو عدد العينات.

model_l2 = LinearSVC(penalty="l2", loss="squared_hinge", dual=True)
Cs = np.logspace(-8, 4, 11)

labels = [f"fraction: {train_size}" for train_size in train_sizes]
results = {"C": Cs}
for label, train_size in zip(labels, train_sizes):
    cv = ShuffleSplit(train_size=train_size, **shuffle_params)
    train_scores, test_scores = validation_curve(
        model_l2,
        X,
        y,
        param_name="C",
        param_range=Cs,
        cv=cv,
        n_jobs=2,
    )
    results[label] = test_scores.mean(axis=1)
results = pd.DataFrame(results)

import matplotlib.pyplot as plt

fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(12, 6))

# رسم النتائج بدون ضبط 'C'
results.plot(x="C", ax=axes[0], logx=True)
axes[0].set_ylabel("درجة التحقق المتقاطع")
axes[0].set_title("بدون ضبط")

for label in labels:
    best_C = results.loc[results[label].idxmax(), "C"]
    axes[0].axvline(x=best_C, linestyle="--", color="grey", alpha=0.8)

# رسم النتائج بضبط 'C'
for train_size_idx, label in enumerate(labels):
    results_scaled = results[[label]].assign(
        C_scaled=Cs * float(n_samples * np.sqrt(train_sizes[train_size_idx]))
    )
    results_scaled.plot(x="C_scaled", ax=axes[1], logx=True, label=label)
    best_C_scaled = results_scaled["C_scaled"].loc[results[label].idxmax()]
    axes[1].axvline(x=best_C_scaled, linestyle="--", color="grey", alpha=0.8)
axes[1].set_title("ضبط 'C' بواسطة sqrt(1 / n_samples)")

fig.suptitle("تأثير ضبط 'C' بعقوبة L2")
plt.show()

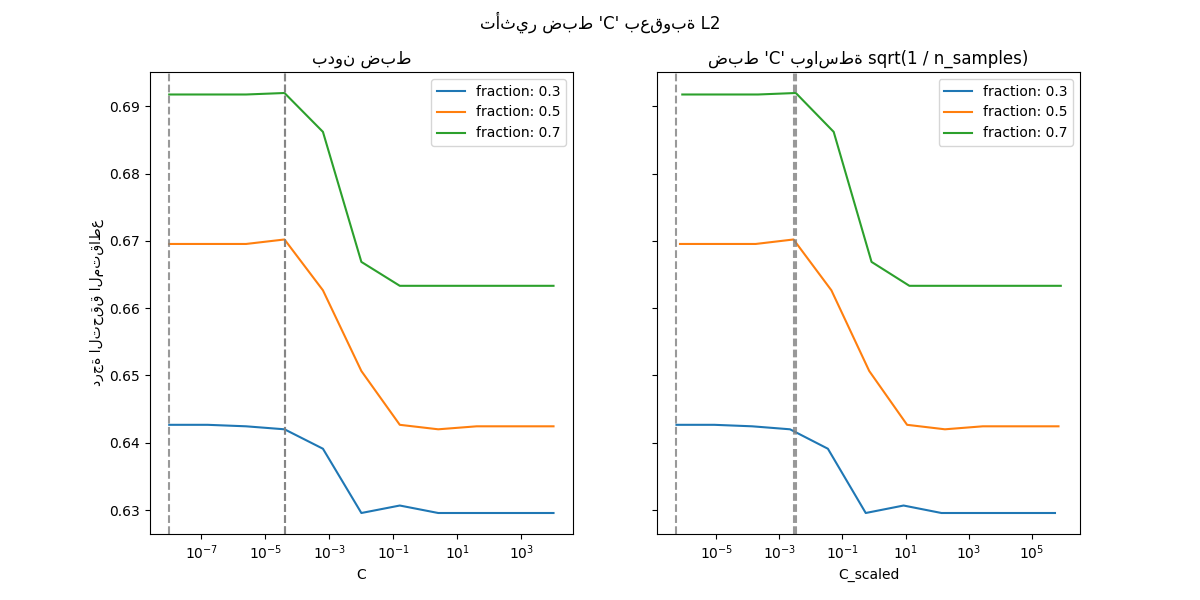
بالنسبة لحالة عقوبة L2، يبدو أن إعادة المعلمة لها تأثير أقل على استقرار القيمة المثلى للانتظام. يحدث الانتقال خارج منطقة الإفراط في الملاءمة في نطاق أكثر انتشارا، ولا يبدو أن الدقة تتدهور إلى مستوى الصدفة.

جرب زيادة القيمة إلى 'n_splits=1_000' للحصول على نتائج أفضل في حالة L2، والتي لا تظهر هنا بسبب القيود على منشئ التوثيق.

Related examples

عقوبة L1 والندرة في الانحدار اللوجستي

عقوبة L1 والندرة في الانحدار اللوجستي

مقارنة بين البحث الشبكي وتقليص الخيارات المتتابع

مقارنة بين البحث الشبكي وتقليص الخيارات المتتابع

نسب الاحتمال الطبقي لقياس أداء التصنيف

نسب الاحتمال الطبقي لقياس أداء التصنيف

عمليات التقسيم المتتالية

عمليات التقسيم المتتالية