ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

معاملات SVM ذات الدالة الشعاعية الأساسية#

يوضح هذا المثال تأثير معاملي "جاما" و "سي" في دالة النواة ذات الدالة الشعاعية الأساسية (RBF) في SVM.

بديهياً، يحدد معامل "جاما" مدى تأثير مثال التدريب الواحد، حيث تشير القيم المنخفضة إلى "بعيد" والقيم العالية إلى "قريب". ويمكن اعتبار معاملات "جاما" على أنها عكس نصف قطر تأثير العينات التي يختارها النموذج كمتجهات دعم.

يتناسب معامل "سي" مع التصنيف الصحيح لأمثلة التدريب مقابل تعظيم هامش دالة القرار. بالنسبة للقيم الأكبر من "سي"، سيتم قبول هامش أصغر إذا كانت دالة القرار أفضل في تصنيف جميع نقاط التدريب بشكل صحيح. وستشجع قيمة "سي" المنخفضة على هامش أكبر، وبالتالي دالة قرار أبسط، على حساب دقة التدريب. وبعبارة أخرى، يتصرف "سي" كمعامل تنظيم في SVM.

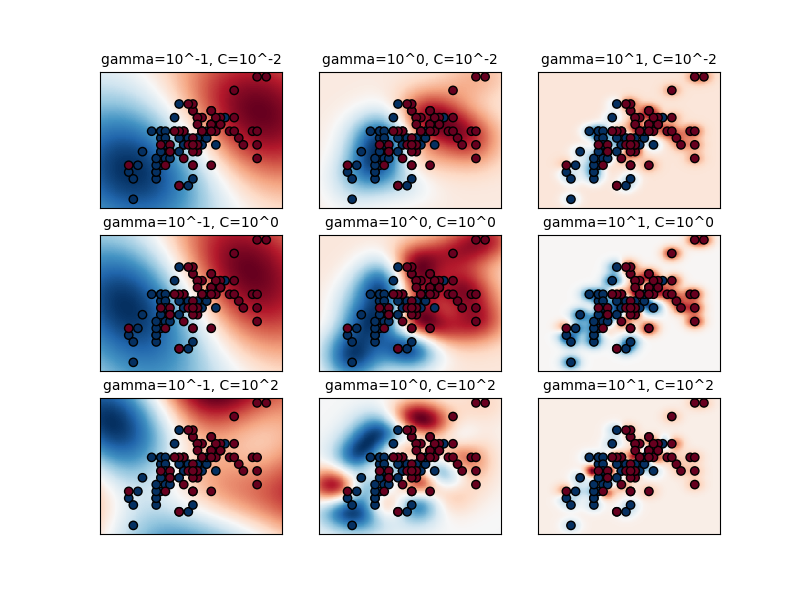
الرسم البياني الأول هو تصور لدالة القرار لمجموعة من قيم المعاملات في مشكلة تصنيف مبسطة تتضمن ميزتين مستهدفتين فقط وفئتين ممكنتين (تصنيف ثنائي). تجدر الإشارة إلى أن هذا النوع من الرسم البياني غير ممكن في المشاكل التي تحتوي على المزيد من الميزات أو الفئات المستهدفة.

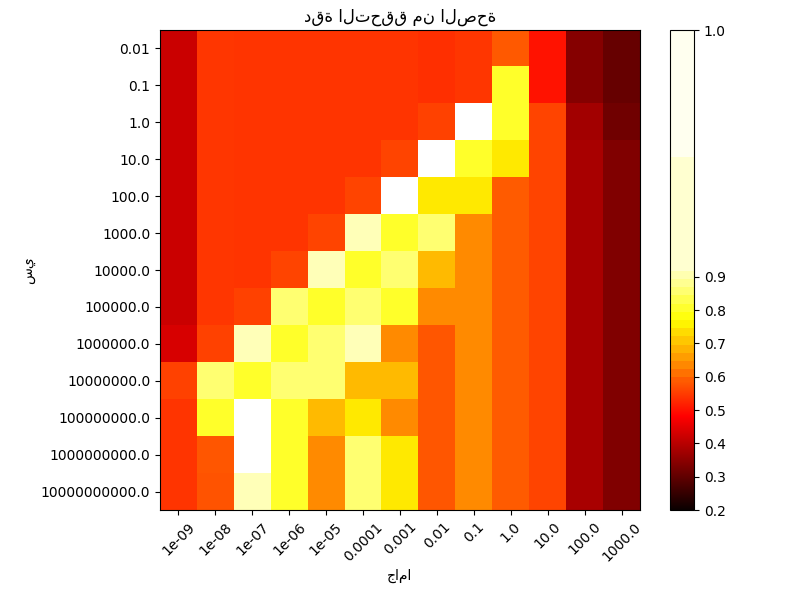
الرسم البياني الثاني هو خريطة حرارية لدقة التصنيف عبر التحقق من صحة دالة التصنيف كدالة في "سي" و"جاما". في هذا المثال، نستكشف شبكة كبيرة نسبياً لأغراض التوضيح. في الممارسة العملية، تكون الشبكة اللوغاريتمية من 10^-3 إلى 10^3 كافية عادةً. إذا كانت أفضل المعاملات تقع على حدود الشبكة، فيمكن تمديدها في ذلك الاتجاه في عملية البحث اللاحقة.

تجدر الإشارة إلى أن خريطة الحرارة لها تدرج لوني خاص مع قيمة وسطى قريبة من قيم الدرجات لأفضل النماذج أداءً بحيث يسهل تمييزها في لمح البصر.

سلوك النموذج حساس للغاية لمعامل "جاما". إذا كانت "جاما" كبيرة جداً، فإن نصف قطر منطقة تأثير متجهات الدعم يشمل متجه الدعم نفسه، ولا يمكن لأي كمية من التنظيم باستخدام "سي" أن تمنع الإفراط في التحديد.

عندما تكون "جاما" صغيرة جداً، يكون النموذج مقيدًا للغاية ولا يمكنه التقاط تعقيد أو "شكل" البيانات. ستتضمن منطقة تأثير أي متجه دعم مختار مجموعة بيانات التدريب بأكملها. سيتصرف النموذج الناتج بشكل مشابه للنموذج الخطي مع مجموعة من المستويات الفاصلة التي تفصل مراكز الكثافة العالية لأي زوج من الفئات.

بالنسبة للقيم المتوسطة، يمكننا أن نرى في الرسم البياني الثاني أن النماذج الجيدة يمكن العثور عليها على قطري "سي" و"جاما". يمكن جعل النماذج الملساء (قيم "جاما" المنخفضة) أكثر تعقيدًا عن طريق زيادة أهمية تصنيف كل نقطة بشكل صحيح (قيم "سي" الأكبر) وبالتالي قطري النماذج ذات الأداء الجيد.

أخيرًا، يمكننا أيضًا ملاحظة أنه بالنسبة لبعض القيم المتوسطة لـ "جاما"، نحصل على نماذج ذات أداء متساوٍ عندما تصبح "سي" كبيرة جدًا. وهذا يشير إلى أن مجموعة متجهات الدعم لا تتغير بعد الآن. يعمل نصف قطر دالة RBF بمفرده كمنظم هيكلي جيد. زيادة "سي" أكثر لا تساعد، على الأرجح لأنه لا توجد نقاط تدريب أخرى في الانتهاك (داخل الهامش أو مصنفة بشكل خاطئ)، أو على الأقل لا يمكن العثور على حل أفضل. نظرًا لتساوي الدرجات، قد يكون من المنطقي استخدام قيم "سي" الأصغر، حيث تزيد قيم "سي" العالية بشكل عام من وقت الملاءمة.

من ناحية أخرى، تؤدي قيم "سي" المنخفضة بشكل عام إلى المزيد من متجهات الدعم، والتي قد تزيد من وقت التنبؤ. لذلك، ينطوي خفض قيمة "سي" على مفاضلة بين وقت الملاءمة ووقت التنبؤ.

يجب أن نلاحظ أيضًا أن الاختلافات الصغيرة في الدرجات ناتجة عن التقسيمات العشوائية لإجراء التحقق من الصحة المتقاطع. يمكن تنعيم هذه التغيرات الزائفة عن طريق زيادة عدد تكرارات CV "n_splits" على حساب وقت الحساب. ستؤدي زيادة عدد خطوات "C_range" و"gamma_range" إلى زيادة دقة خريطة الحرارة للبارامترات فائقة الدقة.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

فئة فائدة لنقل نقطة الوسط لمخطط الألوان ليكون حول قيم الاهتمام.

import numpy as np
from matplotlib.colors import Normalize


class MidpointNormalize (Normalize):
    def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
        self.midpoint = midpoint
        Normalize.__init__(self, vmin, vmax, clip)

    def __call__(self, value, clip=None):
        x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
        return np.ma.masked_array(np.interp(value, x, y))

تحميل وإعداد مجموعة البيانات#

مجموعة البيانات للبحث الشبكي

from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target

مجموعة بيانات لتصور دالة القرار: نحتفظ فقط بأول ميزتين في X ونأخذ عينة فرعية من مجموعة البيانات للاحتفاظ بفئتين فقط وجعلها مشكلة تصنيف ثنائي.

X_2d = X[:, :2]
X_2d = X_2d[y > 0]
y_2d = y[y > 0]
y_2d -= 1

عادة ما تكون فكرة جيدة لقياس البيانات لتدريب SVM. نحن نغش قليلاً في هذا المثال في قياس جميع البيانات، بدلاً من ملاءمة التحويل على مجموعة التدريب وتطبيقه فقط على مجموعة الاختبار.

from  sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X = scaler.fit_transform(X)
X_2d = scaler.fit_transform(X_2d)

تدريب المصنفات#

للبحث الأولي، تكون الشبكة اللوغاريتمية ذات الأساس 10 مفيدة غالبًا. باستخدام أساس 2، يمكن تحقيق ضبط أدق ولكن بتكلفة أعلى بكثير.

from sklearn.model_selection import GridSearchCV, StratifiedShuffleSplit
from sklearn.svm import SVC

C_range = np.logspace(-2, 10, 13)
gamma_range = np.logspace(-9, 3, 13)
param_grid = dict(gamma=gamma_range, C=C_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=cv)
grid.fit(X, y)

print(
"أفضل المعاملات هي %s مع درجة %0.2f"
% (grid.best_params_, grid.best_score_)
)

أفضل المعاملات هي {'C': np.float64(1.0), 'gamma': np.float64(0.1)} مع درجة 0.97

الآن نحتاج إلى ملاءمة مصنف لجميع المعاملات في الإصدار 2D (نستخدم مجموعة أصغر من المعاملات هنا لأنها تستغرق بعض الوقت للتدريب)

C_2d_range = [1e-2, 1, 1e2]
gamma_2d_range = [1e-1, 1, 1e1]
classifiers = []
for C in C_2d_range:
    for gamma in gamma_2d_range:
        clf = SVC(C=C, gamma=gamma)
        clf.fit(X_2d, y_2d)
        classifiers.append((C, gamma, clf))

التصور#

رسم تصور لتأثير المعاملات

import matplotlib.pyplot as plt

plt.figure(figsize=(8, 6))
xx, yy = np.meshgrid(np.linspace(-3, 3, 200), np.linspace(-3, 3, 200))
for k, (C, gamma, clf) in enumerate(classifiers):
    # تقييم دالة القرار في شبكة
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # تصور دالة القرار لهذه المعاملات
    plt.subplot(len(C_2d_range), len(gamma_2d_range), k + 1)
    plt.title("gamma=10^%d, C=10^%d" % (np.log10(gamma), np.log10(C)), size="medium")

    # تصور تأثير المعامل على دالة القرار
    plt.pcolormesh(xx, yy, -Z, cmap=plt.cm.RdBu)
    plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, cmap=plt.cm.RdBu_r, edgecolors="k")
    plt.xticks(())
    plt.yticks(())
    plt.axis("tight")

scoring = grid.cv_results_["mean_test_score"].reshape(len(C_range), len(gamma_range))

gamma=10^-1, C=10^-2, gamma=10^0, C=10^-2, gamma=10^1, C=10^-2, gamma=10^-1, C=10^0, gamma=10^0, C=10^0, gamma=10^1, C=10^0, gamma=10^-1, C=10^2, gamma=10^0, C=10^2, gamma=10^1, C=10^2

رسم خريطة حرارية لدقة التحقق من صحة دالة التصنيف كدالة في "جاما" و"سي"

يتم ترميز الدرجات كألوان مع مخطط الألوان الساخن الذي يتراوح من الأحمر الداكن إلى الأصفر الساطع. نظرًا لأن الدرجات الأكثر إثارة للاهتمام تقع جميعها في النطاق من 0.92 إلى 0.97، نستخدم معيارًا مخصصًا لوضع نقطة الوسط عند 0.92 بحيث يسهل تصور الاختلافات الصغيرة في قيم الدرجات في النطاق المثير للاهتمام بينما لا يتم طي جميع قيم الدرجات المنخفضة بشكل وحشي إلى نفس اللون.

plt.figure(figsize=(8, 6))
plt.subplots_adjust(left=0.2, right=0.95, bottom=0.15, top=0.95)
plt.imshow(
    scoring,
    interpolation="nearest",
    cmap=plt.cm.hot,
    norm=MidpointNormalize(vmin=0.2, midpoint=0.92),
)
plt.xlabel("جاما")
plt.ylabel("سي")
plt.colorbar()
plt.xticks(np.arange(len(gamma_range)), gamma_range, rotation=45)
plt.yticks(np.arange(len(C_range)), C_range)
plt.title("دقة التحقق من الصحة")
plt.show()