ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

رسم احتمالية التصنيف#

ارسم احتمالية التصنيف لمصنفات مختلفة. نستخدم مجموعة بيانات من 3 فئات، ونصنفها باستخدام مصنف الدعم الموجه، والانحدار اللوجستي المعاقب L1 وL2 (متعدد الحدود متعدد الفئات)، وإصدار One-Vs-Rest مع الانحدار اللوجستي، وتصنيف عملية جاوس.

SVC الخطي ليس مصنف احتمالي بشكل افتراضي، ولكنه يحتوي على خيار معايرة مدمج مُمكّن في هذا المثال (probability=True).

الانحدار اللوجستي مع One-Vs-Rest ليس مصنف متعدد الفئات بشكل افتراضي. ونتيجة لذلك، يواجه صعوبة أكبر في فصل الفئة 2 و3 عن المصنفات الأخرى.

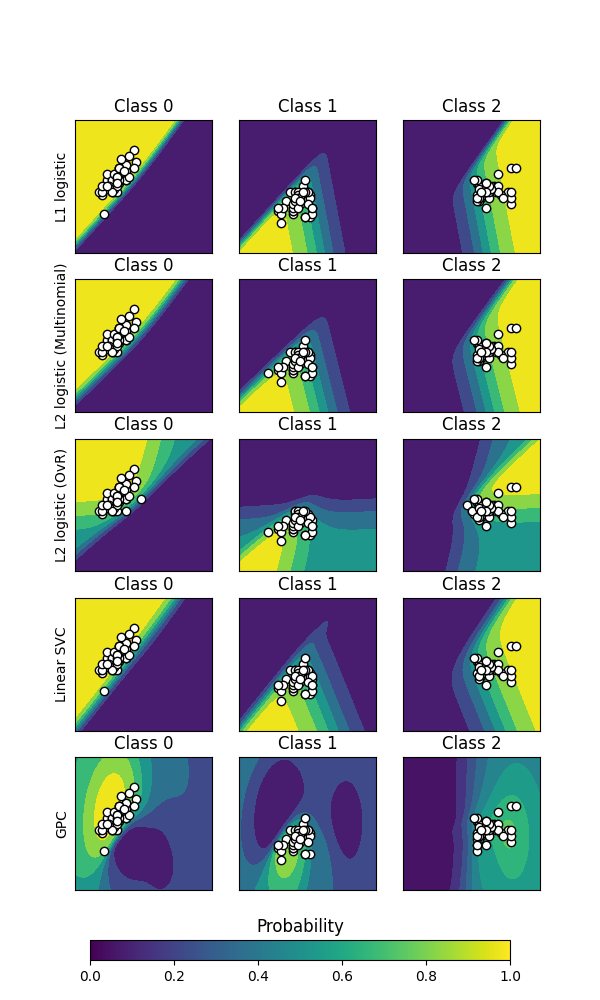
Class 0, Class 1, Class 2, Class 0, Class 1, Class 2, Class 0, Class 1, Class 2, Class 0, Class 1, Class 2, Class 0, Class 1, Class 2, Probability

Accuracy (train) for L1 logistic: 83.3%
Accuracy (train) for L2 logistic (Multinomial): 82.7%
Accuracy (train) for L2 logistic (OvR): 79.3%
Accuracy (train) for Linear SVC: 82.0%
Accuracy (train) for GPC: 82.7%

# المؤلفون: مطوري سكايت-ليرن
# معرف-ترخيص-SPDX: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm

from sklearn import datasets
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.multiclass import OneVsRestClassifier
from sklearn.svm import SVC

iris = datasets.load_iris()
X = iris.data[:, 0:2]  # نأخذ فقط الخاصيتين الأوليين للتصور
y = iris.target

n_features = X.shape[1]

C = 10
kernel = 1.0 * RBF([1.0, 1.0])  # لتصنيف GPC

# إنشاء مصنفات مختلفة.
classifiers = {
    "L1 logistic": LogisticRegression(C=C, penalty="l1", solver="saga", max_iter=10000),
    "L2 logistic (Multinomial)": LogisticRegression(
        C=C, penalty="l2", solver="saga", max_iter=10000
    ),
    "L2 logistic (OvR)": OneVsRestClassifier(
        LogisticRegression(C=C, penalty="l2", solver="saga", max_iter=10000)
    ),
    "Linear SVC": SVC(kernel="linear", C=C, probability=True, random_state=0),
    "GPC": GaussianProcessClassifier(kernel),
}

n_classifiers = len(classifiers)

fig, axes = plt.subplots(
    nrows=n_classifiers,
    ncols=len(iris.target_names),
    figsize=(3 * 2, n_classifiers * 2),
)
for classifier_idx, (name, classifier) in enumerate(classifiers.items()):
    y_pred = classifier.fit(X, y).predict(X)
    accuracy = accuracy_score(y, y_pred)
    print(f"Accuracy (train) for {name}: {accuracy:0.1%}")
    for label in np.unique(y):
        # ارسم تقدير الاحتمالية المقدم من المصنف
        disp = DecisionBoundaryDisplay.from_estimator(
            classifier,
            X,
            response_method="predict_proba",
            class_of_interest=label,
            ax=axes[classifier_idx, label],
            vmin=0,
            vmax=1,
        )
        axes[classifier_idx, label].set_title(f"Class {label}")
        # ارسم البيانات المتوقعة للانتماء إلى الفئة المعطاة
        mask_y_pred = y_pred == label
        axes[classifier_idx, label].scatter(
            X[mask_y_pred, 0], X[mask_y_pred, 1], marker="o", c="w", edgecolor="k"
        )
        axes[classifier_idx, label].set(xticks=(), yticks=())
    axes[classifier_idx, 0].set_ylabel(name)

ax = plt.axes([0.15, 0.04, 0.7, 0.02])
plt.title("Probability")
_ = plt.colorbar(
    cm.ScalarMappable(norm=None, cmap="viridis"), cax=ax, orientation="horizontal"
)

plt.show()