ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
التنبؤات الاحتمالية مع تصنيف العملية الغاوسية (GPC)#
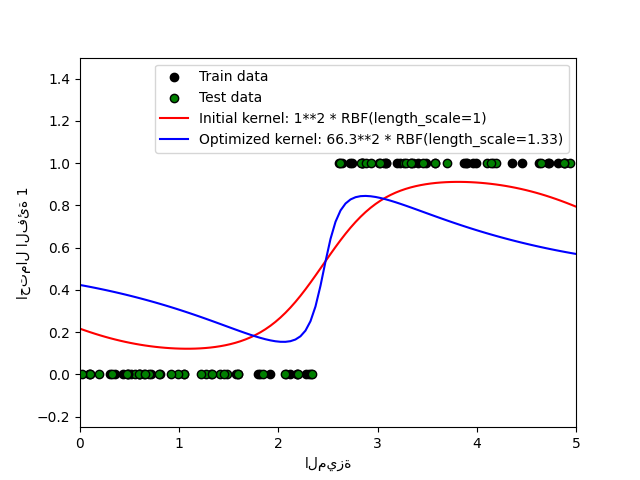
يوضح هذا المثال الاحتمال المتوقع لـ GPC لنواة RBF مع خيارات مختلفة للمعلمات الفائقة. يُظهر الشكل الأول الاحتمال المتوقع لـ GPC مع معلمات فائقة تم اختيارها عشوائيًا ومع المعلمات الفائقة المقابلة لأكبر احتمال هامشي لوغاريتمي (LML).
بينما تتمتع المعلمات الفائقة التي تم اختيارها عن طريق تحسين LML باحتمال هامشي لوغاريتمي أكبر بكثير ، فإنها تعمل بشكل أسوأ قليلاً وفقًا لـ log-loss على بيانات الاختبار. يُظهر الشكل أن هذا بسبب أنها تُظهر تغيرًا حادًا في احتمالات الفئة عند حدود الفئة (وهو أمر جيد) ولكن لديها احتمالات متوقعة قريبة من 0.5 بعيدًا عن حدود الفئة (وهو أمر سيئ). يحدث هذا التأثير غير المرغوب فيه بسبب تقريب لابلاس المستخدم داخليًا بواسطة GPC.
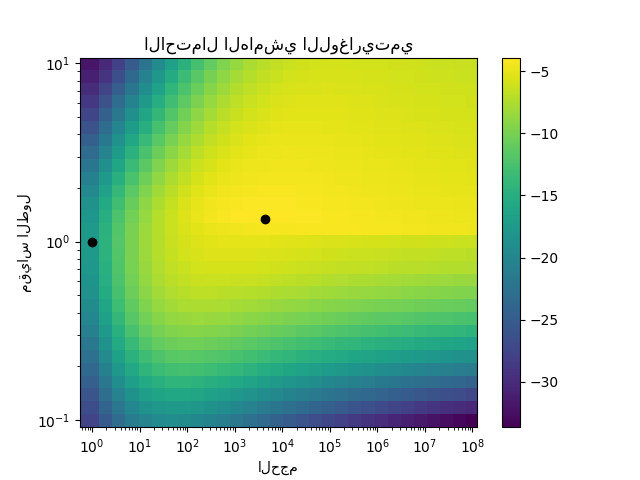
يُظهر الشكل الثاني الاحتمال الهامشي اللوغاريتمي لاختيارات مختلفة لمعلمات النواة الفائقة ، مع إبراز خياري المعلمات الفائقة المستخدمة في الشكل الأول بنقاط سوداء.
الاحتمال الهامشي اللوغاريتمي (أولي): -17.598
الاحتمال الهامشي اللوغاريتمي (محسن): -3.875
الدقة: 1.000 (أولي) 1.000 (محسن)
Log-loss: 0.214 (أولي) 0.319 (محسن)
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from matplotlib import pyplot as plt
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import accuracy_score, log_loss
# توليد البيانات
train_size = 50
rng = np.random.RandomState(0)
X = rng.uniform(0, 5, 100)[:, np.newaxis]
y = np.array(X[:, 0] > 2.5, dtype=int)
# تحديد عمليات غاوسية بمعلمات فائقة ثابتة ومحسنة
gp_fix = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0), optimizer=None)
gp_fix.fit(X[:train_size], y[:train_size])
gp_opt = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0))
gp_opt.fit(X[:train_size], y[:train_size])
print(
"الاحتمال الهامشي اللوغاريتمي (أولي): %.3f"
% gp_fix.log_marginal_likelihood(gp_fix.kernel_.theta)
)
print(
"الاحتمال الهامشي اللوغاريتمي (محسن): %.3f"
% gp_opt.log_marginal_likelihood(gp_opt.kernel_.theta)
)
print(
"الدقة: %.3f (أولي) %.3f (محسن)"
% (
accuracy_score(y[:train_size], gp_fix.predict(X[:train_size])),
accuracy_score(y[:train_size], gp_opt.predict(X[:train_size])),
)
)
print(
"Log-loss: %.3f (أولي) %.3f (محسن)"
% (
log_loss(y[:train_size], gp_fix.predict_proba(X[:train_size])[:, 1]),
log_loss(y[:train_size], gp_opt.predict_proba(X[:train_size])[:, 1]),
)
)
# رسم التوزيعات اللاحقة
plt.figure()
plt.scatter(
X[:train_size, 0], y[:train_size], c="k", label="Train data", edgecolors=(0, 0, 0)
)
plt.scatter(
X[train_size:, 0], y[train_size:], c="g", label="Test data", edgecolors=(0, 0, 0)
)
X_ = np.linspace(0, 5, 100)
plt.plot(
X_,
gp_fix.predict_proba(X_[:, np.newaxis])[:, 1],
"r",
label="Initial kernel: %s" % gp_fix.kernel_,
)
plt.plot(
X_,
gp_opt.predict_proba(X_[:, np.newaxis])[:, 1],
"b",
label="Optimized kernel: %s" % gp_opt.kernel_,
)
plt.xlabel("الميزة")
plt.ylabel("احتمال الفئة 1")
plt.xlim(0, 5)
plt.ylim(-0.25, 1.5)
plt.legend(loc="best")
# رسم المشهد LML
plt.figure()
theta0 = np.logspace(0, 8, 30)
theta1 = np.logspace(-1, 1, 29)
Theta0, Theta1 = np.meshgrid(theta0, theta1)
LML = [
[
gp_opt.log_marginal_likelihood(np.log([Theta0[i, j], Theta1[i, j]]))
for i in range(Theta0.shape[0])
]
for j in range(Theta0.shape[1])
]
LML = np.array(LML).T
plt.plot(
np.exp(gp_fix.kernel_.theta)[0], np.exp(gp_fix.kernel_.theta)[1], "ko", zorder=10
)
plt.plot(
np.exp(gp_opt.kernel_.theta)[0], np.exp(gp_opt.kernel_.theta)[1], "ko", zorder=10
)
plt.pcolor(Theta0, Theta1, LML)
plt.xscale("log")
plt.yscale("log")
plt.colorbar()
plt.xlabel("الحجم")
plt.ylabel("مقياس الطول")
plt.title("الاحتمال الهامشي اللوغاريتمي")
plt.show()
Total running time of the script: (0 minutes 2.344 seconds)
Related examples
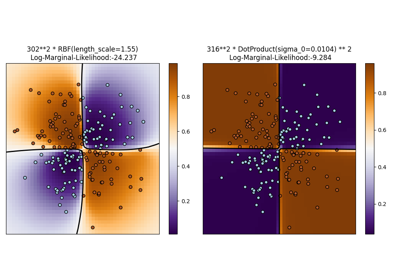
توضيح تصنيف العملية الغاوسية (GPC) على مجموعة بيانات XOR
قدرة انحدار العمليات الغاوسية (GPR) على تقدير مستوى ضوضاء البيانات
تصنيف العملية الغاوسية (GPC) على مجموعة بيانات iris