ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

مقارنة انحدار kernel ridge وانحدار العمليات الغاوسية#

يوضح هذا المثال الاختلافات بين انحدار kernel ridge وانحدار العمليات الغاوسية.

يستخدم كل من انحدار kernel ridge وانحدار العمليات الغاوسية ما يسمى "kernel trick" لجعل نماذجهما معبرة بما يكفي لملاءمة بيانات التدريب. ومع ذلك ، فإن مشاكل التعلم الآلي التي تم حلها بواسطة الطريقتين مختلفة بشكل كبير.

سيجد انحدار kernel ridge دالة الهدف التي تقلل من دالة الخسارة (متوسط الخطأ التربيعي).

بدلاً من إيجاد دالة هدف واحدة ، يستخدم انحدار العمليات الغاوسية نهجًا احتماليًا: يتم تحديد التوزيع اللاحق الغاوسي على دوال الهدف بناءً على نظرية Bayes ، وبالتالي يتم دمج الاحتمالات السابقة على دوال الهدف مع دالة احتمالية محددة بواسطة بيانات التدريب المرصودة لتقديم تقديرات للتوزيعات اللاحقة.

سنوضح هذه الاختلافات بمثال وسنركز أيضًا على ضبط المعلمات الفائقة للنواة.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

توليد مجموعة بيانات#

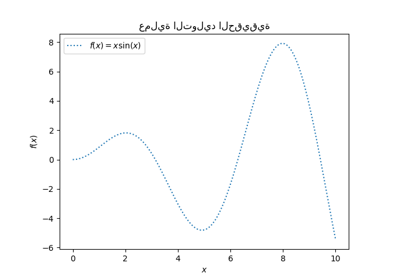
نقوم بإنشاء مجموعة بيانات اصطناعية. ستأخذ عملية التوليد الحقيقية متجهًا أحادي البعد وتحسب جيبها. لاحظ أن فترة هذا الجيب هي \(2 \pi\). سنعيد استخدام هذه المعلومات لاحقًا في هذا المثال.

import numpy as np

rng = np.random.RandomState(0)
data = np.linspace(0, 30, num=1_000).reshape(-1, 1)
target = np.sin(data).ravel()

الآن ، يمكننا تخيل سيناريو حيث نحصل على ملاحظات من هذه العملية الحقيقية. ومع ذلك ، سنضيف بعض التحديات:

ستكون القياسات صاخبة ؛
ستكون العينات من بداية الإشارة فقط متاحة.

training_sample_indices = rng.choice(np.arange(0, 400), size=40, replace=False)
training_data = data[training_sample_indices]
training_noisy_target = target[training_sample_indices] + 0.5 * rng.randn(
    len(training_sample_indices)
)

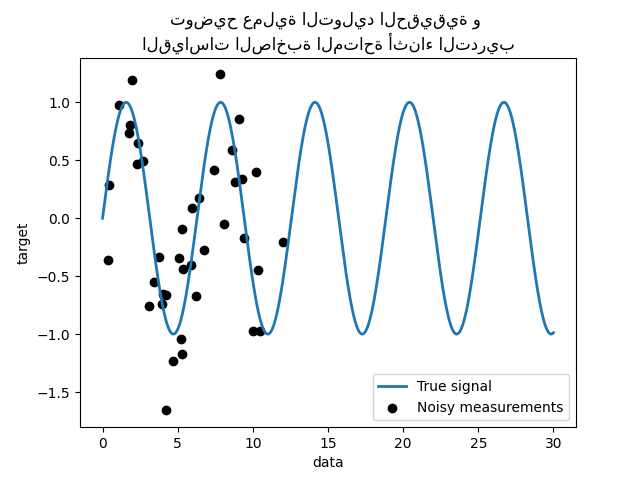
دعونا نرسم الإشارة الحقيقية والقياسات الصاخبة المتاحة للتدريب.

import matplotlib.pyplot as plt

plt.plot(data, target, label="True signal", linewidth=2)
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "توضيح عملية التوليد الحقيقية و \n"
    "القياسات الصاخبة المتاحة أثناء التدريب"
)

توضيح عملية التوليد الحقيقية و القياسات الصاخبة المتاحة أثناء التدريب

حدود نموذج خطي بسيط#

أولاً ، نود تسليط الضوء على حدود النموذج الخطي بالنظر إلى مجموعة البيانات الخاصة بنا. نقوم بملاءمة Ridge ونتحقق من تنبؤات هذا النموذج على مجموعة البيانات الخاصة بنا.

from sklearn.linear_model import Ridge

ridge = Ridge().fit(training_data, training_noisy_target)

plt.plot(data, target, label="True signal", linewidth=2)
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(data, ridge.predict(data), label="Ridge regression")
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("حدود نموذج خطي مثل ridge")

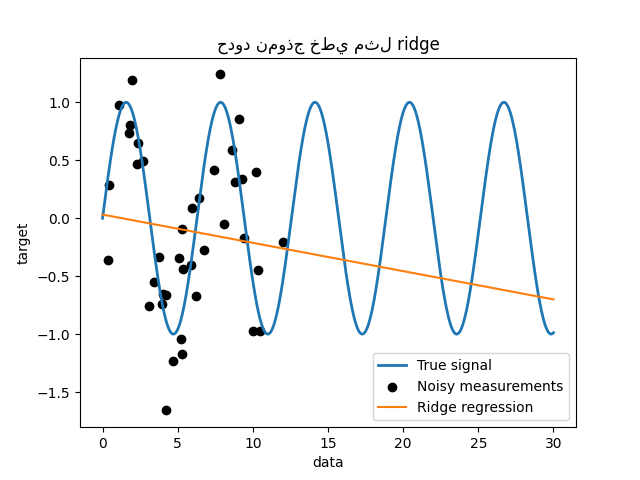
مثل هذا المنحدر ridge لا يتناسب مع البيانات لأنه ليس معبرًا بما فيه الكفاية.

طرق النواة: kernel ridge و العملية الغاوسية#

Kernel ridge#

يمكننا جعل النموذج الخطي السابق أكثر تعبيرًا باستخدام ما يسمى النواة. النواة هي تضمين من مساحة الميزة الأصلية إلى أخرى. ببساطة ، يتم استخدامه لتعيين بياناتنا الأصلية في مساحة ميزة أحدث وأكثر تعقيدًا. يتم تعريف هذه المساحة الجديدة صراحةً من خلال اختيار النواة.

في حالتنا ، نعلم أن عملية التوليد الحقيقية هي دالة دورية. يمكننا استخدام نواة ExpSineSquared التي تسمح باستعادة الدورية. الفئة KernelRidge ستقبل مثل هذه النواة.

استخدام هذا النموذج مع النواة يعادل تضمين البيانات باستخدام دالة التعيين للنواة ثم تطبيق انحدار ridge. من الناحية العملية ، لا يتم تعيين البيانات بشكل صريح ؛ بدلاً من ذلك ، حاصل الضرب النقطي بين العينات في مساحة الميزة ذات الأبعاد الأعلى يتم حسابه باستخدام "kernel trick".

وبالتالي ، دعونا نستخدم KernelRidge .

import time

from sklearn.gaussian_process.kernels import ExpSineSquared
from sklearn.kernel_ridge import KernelRidge

kernel_ridge = KernelRidge(kernel=ExpSineSquared())

start_time = time.time()
kernel_ridge.fit(training_data, training_noisy_target)
print(
    f"ملاءمة KernelRidge مع النواة الافتراضية: {time.time() - start_time:.3f} ثانية"
)

ملاءمة KernelRidge مع النواة الافتراضية: 0.001 ثانية

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(
    data,
    kernel_ridge.predict(data),
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "انحدار Kernel ridge مع  exponential sine squared\n "
    "النواة باستخدام المعلمات الفائقة الافتراضية"
)

انحدار Kernel ridge مع exponential sine squared النواة باستخدام المعلمات الفائقة الافتراضية

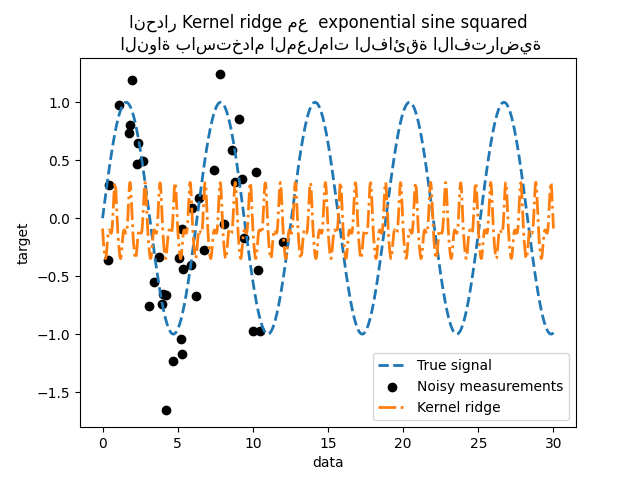
هذا النموذج المجهز غير دقيق. في الواقع ، لم نقم بتعيين معلمات النواة واستخدمنا المعلمات الافتراضية بدلاً من ذلك. يمكننا فحصها.

kernel_ridge.kernel

ExpSineSquared(length_scale=1, periodicity=1)

تحتوي نواتنا على معلمتين: مقياس الطول والدورية. بالنسبة لمجموعة البيانات الخاصة بنا ، نستخدم sin كعملية توليد ، مما يعني \(2 \pi\)-دورية للإشارة. القيمة الافتراضية للمعامل هي \(1\) ، وهذا يفسر التردد العالي الملاحظ في تنبؤات نموذجنا. يمكن استخلاص استنتاجات مماثلة مع معامل مقياس الطول. وبالتالي ، يخبرنا أن معلمات النواة بحاجة إلى الضبط. سنستخدم بحثًا عشوائيًا لضبط المعلمات المختلفة لنموذج kernel ridge: المعامل alpha ومعلمات النواة.

from scipy.stats import loguniform

from sklearn.model_selection import RandomizedSearchCV

param_distributions = {
    "alpha": loguniform(1e0, 1e3),
    "kernel__length_scale": loguniform(1e-2, 1e2),
    "kernel__periodicity": loguniform(1e0, 1e1),
}
kernel_ridge_tuned = RandomizedSearchCV(
    kernel_ridge,
    param_distributions=param_distributions,
    n_iter=500,
    random_state=0,
)
start_time = time.time()
kernel_ridge_tuned.fit(training_data, training_noisy_target)
print(f"الوقت اللازم لملاءمة KernelRidge: {time.time() - start_time:.3f} ثانية")

الوقت اللازم لملاءمة KernelRidge: 4.548 ثانية

أصبحت ملاءمة النموذج الآن أكثر تكلفة من الناحية الحسابية نظرًا لأنه يتعين علينا تجربة عدة مجموعات من المعلمات الفائقة. يمكننا إلقاء نظرة على المعلمات الفائقة التي تم العثور عليها للحصول على بعض الحدس.

kernel_ridge_tuned.best_params_

{'alpha': np.float64(1.991584977345022), 'kernel__length_scale': np.float64(0.7986499491396734), 'kernel__periodicity': np.float64(6.6072758064261095)}

بالنظر إلى أفضل المعلمات ، نرى أنها مختلفة عن الافتراضيات. نرى أيضًا أن الدورية أقرب إلى القيمة المتوقعة: \(2 \pi\). يمكننا الآن فحص تنبؤات kernel ridge المضبوط لدينا.

start_time = time.time()
predictions_kr = kernel_ridge_tuned.predict(data)
print(f"الوقت اللازم للتنبؤ بـ KernelRidge: {time.time() - start_time:.3f} ثانية")

الوقت اللازم للتنبؤ بـ KernelRidge: 0.002 ثانية

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "انحدار Kernel ridge مع  exponential sine squared\n "
    "النواة باستخدام المعلمات الفائقة المضبوطة"
)

انحدار Kernel ridge مع exponential sine squared النواة باستخدام المعلمات الفائقة المضبوطة

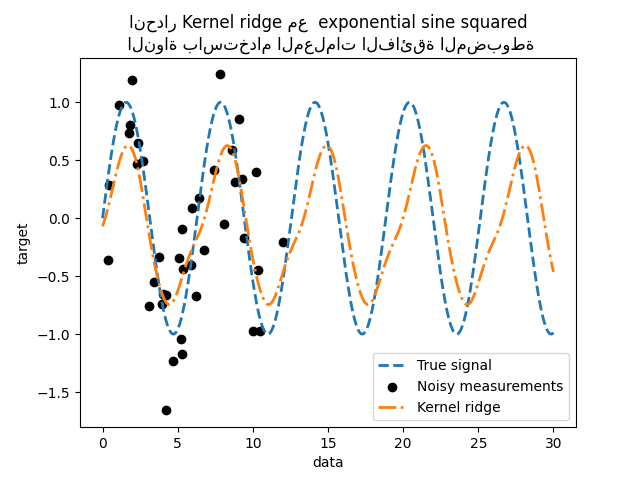
نحصل على نموذج أكثر دقة. ما زلنا نلاحظ بعض الأخطاء ويرجع ذلك أساسًا إلى الضوضاء المضافة إلى مجموعة البيانات.

انحدار العملية الغاوسية#

الآن ، سنستخدم GaussianProcessRegressor لملاءمة نفس مجموعة البيانات. عند تدريب عملية غاوسية ، يتم تحسين المعلمات الفائقة للنواة أثناء عملية الملاءمة. ليست هناك حاجة لبحث خارجي عن المعلمات الفائقة. هنا ، نقوم بإنشاء نواة أكثر تعقيدًا قليلاً من

kernel ridge: نضيف

WhiteKernel التي تُستخدم لـ تقدير الضوضاء في مجموعة البيانات.

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel

kernel = 1.0 * ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) + WhiteKernel(
    1e-1
)
gaussian_process = GaussianProcessRegressor(kernel=kernel)
start_time = time.time()
gaussian_process.fit(training_data, training_noisy_target)
print(
    f"الوقت اللازم لملاءمة GaussianProcessRegressor: {time.time() - start_time:.3f} ثانية"
)

الوقت اللازم لملاءمة GaussianProcessRegressor: 0.158 ثانية

التكلفة الحسابية لتدريب عملية غاوسية أقل بكثير من تكلفة kernel ridge التي تستخدم بحثًا عشوائيًا. يمكننا التحقق من معلمات النوى التي حسبناها.

gaussian_process.kernel_

0.675**2 * ExpSineSquared(length_scale=1.34, periodicity=6.57) + WhiteKernel(noise_level=0.182)

في الواقع ، نرى أن المعلمات قد تم تحسينها. بالنظر إلى معامل periodicity ، نرى أننا وجدنا فترة قريبة من القيمة النظرية \(2 \pi\). يمكننا الآن إلقاء نظرة على تنبؤات نموذجنا.

start_time = time.time()
mean_predictions_gpr, std_predictions_gpr = gaussian_process.predict(
    data,
    return_std=True,
)
print(
    f"الوقت اللازم للتنبؤ بـ GaussianProcessRegressor: {time.time() - start_time:.3f} ثانية"
)

الوقت اللازم للتنبؤ بـ GaussianProcessRegressor: 0.002 ثانية

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
# رسم تنبؤات kernel ridge
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
# رسم تنبؤات انحدار العملية الغاوسية
plt.plot(
    data,
    mean_predictions_gpr,
    label="Gaussian process regressor",
    linewidth=2,
    linestyle="dotted",
)
plt.fill_between(
    data.ravel(),
    mean_predictions_gpr - std_predictions_gpr,
    mean_predictions_gpr + std_predictions_gpr,
    color="tab:green",
    alpha=0.2,
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("مقارنة بين kernel ridge وانحدار العملية الغاوسية")

مقارنة بين kernel ridge وانحدار العملية الغاوسية

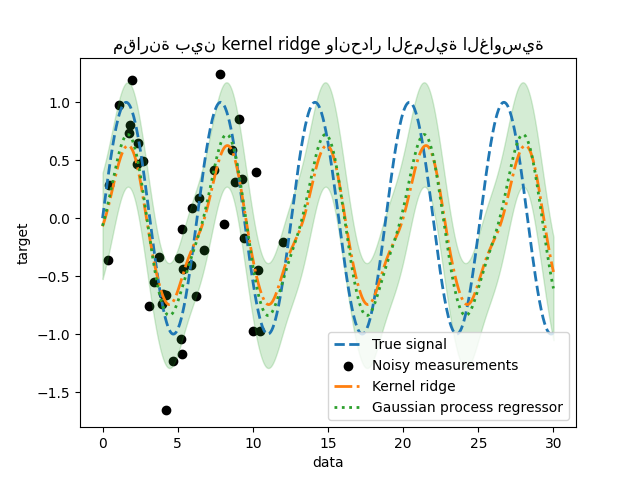
نلاحظ أن نتائج kernel ridge وانحدار العملية الغاوسية متقاربة. ومع ذلك ، يوفر انحدار العملية الغاوسية أيضًا معلومات عدم اليقين التي لا تتوفر مع kernel ridge. نظرًا للصياغة الاحتمالية لدوال الهدف ، يمكن للعملية الغاوسية إخراج الانحراف المعياري (أو التغاير) جنبًا إلى جنب مع متوسط تنبؤات دوال الهدف.

ومع ذلك ، فإن هذا يأتي بتكلفة: الوقت اللازم لحساب التنبؤات يكون أعلى مع العملية الغاوسية.

الخلاصة النهائية#

يمكننا أن نقول كلمة أخيرة بخصوص إمكانية النموذجين للاستقراء. في الواقع ، قدمنا فقط بداية الإشارة كمجموعة تدريب. استخدام نواة دورية يجبر نموذجنا على تكرار النمط الموجود في مجموعة التدريب. باستخدام معلومات النواة هذه جنبًا إلى جنب مع قدرة كلا النموذجين على الاستقراء ، نلاحظ أن النماذج ستستمر في التنبؤ بنمط الجيب.

تسمح العملية الغاوسية بدمج النوى معًا. وبالتالي ، يمكننا ربط: exponential sine squared kernel مع نواة دالة الأساس الشعاعي.

from sklearn.gaussian_process.kernels import RBF

kernel = 1.0 * ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) * RBF(
    length_scale=15, length_scale_bounds="fixed"
) + WhiteKernel(1e-1)
gaussian_process = GaussianProcessRegressor(kernel=kernel)
gaussian_process.fit(training_data, training_noisy_target)
mean_predictions_gpr, std_predictions_gpr = gaussian_process.predict(
    data,
    return_std=True,
)

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
# رسم تنبؤات kernel ridge
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
# رسم تنبؤات انحدار العملية الغاوسية
plt.plot(
    data,
    mean_predictions_gpr,
    label="Gaussian process regressor",
    linewidth=2,
    linestyle="dotted",
)
plt.fill_between(
    data.ravel(),
    mean_predictions_gpr - std_predictions_gpr,
    mean_predictions_gpr + std_predictions_gpr,
    color="tab:green",
    alpha=0.2,
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("تأثير استخدام نواة دالة الأساس الشعاعي")

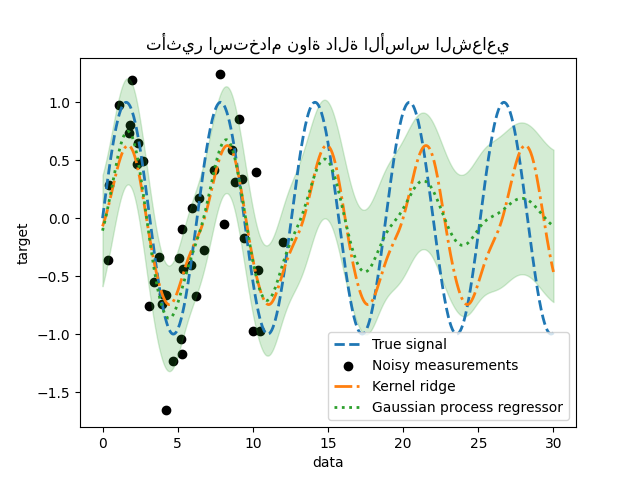
سيؤدي تأثير استخدام نواة دالة الأساس الشعاعي إلى تخفيف تأثير الدورية بمجرد عدم توفر أي عينة في التدريب. كلما ابتعدت عينات الاختبار عن عينات التدريب ، تتقارب التنبؤات نحو متوسطها ويزداد انحرافها المعياري أيضًا.

Total running time of the script: (0 minutes 5.513 seconds)