ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
التنبؤ بمستوى ثاني أكسيد الكربون في مجموعة بيانات Mona Loa باستخدام انحدار العملية الغاوسية (GPR)#
يستند هذا المثال إلى القسم 5.4.3 من "العمليات الغاوسية للتعلم الآلي" [1]. يوضح مثالاً على هندسة النواة المعقدة وتحسين المعلمات الفائقة باستخدام صعود التدرج على الاحتمال الهامشي اللوغاريتمي. تتكون البيانات من متوسط التركيزات الشهرية لثاني أكسيد الكربون في الغلاف الجوي (مقاسة بأجزاء لكل مليون من حيث الحجم (ppm)) التي تم جمعها في مرصد مونا لوا في هاواي ، بين عامي 1958 و 2001. الهدف هو نمذجة تركيز ثاني أكسيد الكربون كدالة للوقت \(t\) واستقراءه للسنوات التي تلي عام 2001.
المراجع
print(__doc__)
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
بناء مجموعة البيانات#
سنشتق مجموعة بيانات من مرصد مونا لوا الذي جمع عينات الهواء. نحن مهتمون بتقدير تركيز ثاني أكسيد الكربون واستقرائه للسنة التالية. أولاً ، نقوم بتحميل مجموعة البيانات الأصلية المتوفرة في OpenML كإطار بيانات pandas. سيتم استبدال هذا بـ Polars بمجرد أن يضيف fetch_openml دعمًا أصليًا له.
from sklearn.datasets import fetch_openml
co2 = fetch_openml(data_id=41187, as_frame=True)
co2.frame.head()
أولاً ، نقوم بمعالجة إطار البيانات الأصلي لإنشاء عمود تاريخ وتحديده مع عمود ثاني أكسيد الكربون.
import polars as pl
co2_data = pl.DataFrame(co2.frame[["year", "month", "day", "co2"]]).select(
pl.date("year", "month", "day"), "co2"
)
co2_data.head()
co2_data["date"].min(), co2_data["date"].max()
(datetime.date(1958, 3, 29), datetime.date(2001, 12, 29))
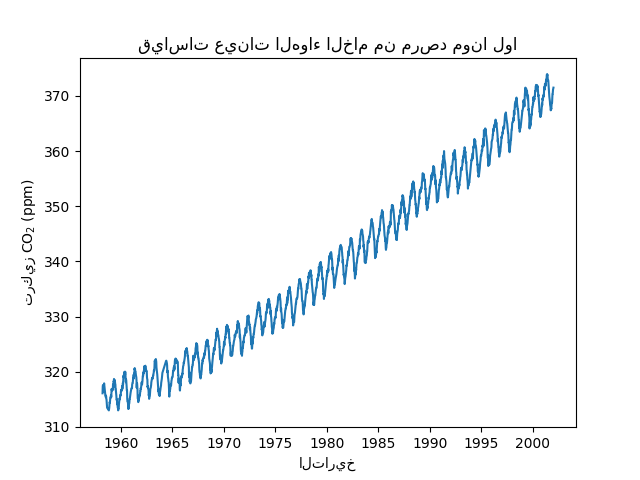
نرى أننا نحصل على تركيز ثاني أكسيد الكربون لبعض الأيام من مارس 1958 إلى ديسمبر 2001. يمكننا رسم هذه المعلومات الخام لفهم أفضل.
import matplotlib.pyplot as plt
plt.plot(co2_data["date"], co2_data["co2"])
plt.xlabel("التاريخ")
plt.ylabel("تركيز CO$_2$ (ppm)")
_ = plt.title("قياسات عينات الهواء الخام من مرصد مونا لوا")
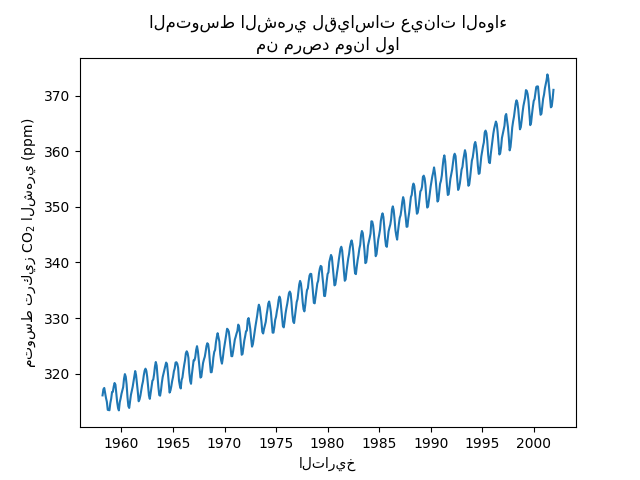
سنقوم بمعالجة مجموعة البيانات عن طريق حساب المتوسط الشهري وإسقاط الأشهر التي لم يتم جمع أي قياسات لها. سيكون لمثل هذه المعالجة تأثير تجانس على البيانات.
co2_data = (
co2_data.sort(by="date")
.group_by_dynamic("date", every="1mo")
.agg(pl.col("co2").mean())
.drop_nulls()
)
plt.plot(co2_data["date"], co2_data["co2"])
plt.xlabel("التاريخ")
plt.ylabel("متوسط تركيز CO$_2$ الشهري (ppm)")
_ = plt.title(
"المتوسط الشهري لقياسات عينات الهواء\nمن مرصد مونا لوا"
)
ستكون الفكرة في هذا المثال هي التنبؤ بتركيز ثاني أكسيد الكربون كدالة للتاريخ. نحن مهتمون أيضًا باستقراء السنوات القادمة بعد عام 2001.
كخطوة أولى ، سنقسم البيانات والهدف المراد تقديره. بما أن البيانات عبارة عن تاريخ ، فسنحولها إلى رقم.
X = co2_data.select(
pl.col("date").dt.year() + pl.col("date").dt.month() / 12
).to_numpy()
y = co2_data["co2"].to_numpy()
تصميم النواة المناسبة#
لتصميم النواة لاستخدامها مع عمليتنا الغاوسية ، يمكننا وضع بعض الافتراضات فيما يتعلق بالبيانات المتوفرة. نلاحظ أن لديها العديد من الخصائص: نرى اتجاهًا تصاعديًا طويل المدى ، وتغير موسمي واضح ، وبعض المخالفات الصغيرة. يمكننا استخدام نواة مناسبة مختلفة من شأنها التقاط هذه الميزات.
أولاً ، يمكن ملاءمة الاتجاه التصاعدي طويل المدى باستخدام نواة دالة أساس شعاعي (RBF) مع معامل مقياس طول كبير. تفرض نواة RBF ذات مقياس الطول الكبير أن يكون هذا المكون سلسًا. لا يتم فرض زيادة في الاتجاه لإعطاء درجة من الحرية لنموذجنا. مقياس الطول المحدد والسعة هما معلمات فائقة حرة.
يتم تفسير التباين الموسمي بواسطة نواة الجيب الأسي التربيعي الدوري مع دورية ثابتة لمدة عام واحد. مقياس الطول لهذا المكون الدوري ، الذي يتحكم في نعومته ، هو معامل حر. من أجل السماح بالانحلال بعيدًا عن الدورية الدقيقة ، يتم أخذ حاصل الضرب مع نواة RBF. يتحكم مقياس الطول لمكون RBF هذا في وقت الانحلال وهو معامل حر إضافي. يُعرف هذا النوع من النواة أيضًا باسم النواة الدورية محليًا.
from sklearn.gaussian_process.kernels import ExpSineSquared
seasonal_kernel = (
2.0**2
* RBF(length_scale=100.0)
* ExpSineSquared(length_scale=1.0, periodicity=1.0, periodicity_bounds="fixed")
)
يتم تفسير المخالفات الصغيرة بواسطة مكون نواة تربيعي نسبي ، والذي سيتم تحديد مقياس طوله ومعامل ألفا ، اللذان يحددان مدى انتشار مقاييس الطول. تُعادل النواة التربيعية النسبية نواة RBF ذات عدة مقاييس طول وستستوعب بشكل أفضل المخالفات المختلفة.
from sklearn.gaussian_process.kernels import RationalQuadratic
irregularities_kernel = 0.5**2 * RationalQuadratic(length_scale=1.0, alpha=1.0)
أخيرًا ، يمكن حساب الضوضاء في مجموعة البيانات بنواة تتكون من مساهمة نواة RBF ، والتي يجب أن تفسر مكونات الضوضاء المترابطة مثل ظواهر الطقس المحلي ، ومساهمة نواة بيضاء للضوضاء البيضاء. السعات النسبية ومقياس طول RBF هي معلمات حرة إضافية.
from sklearn.gaussian_process.kernels import WhiteKernel
noise_kernel = 0.1**2 * RBF(length_scale=0.1) + WhiteKernel(
noise_level=0.1**2, noise_level_bounds=(1e-5, 1e5)
)
وبالتالي ، فإن نواتنا النهائية هي إضافة جميع النوى السابقة.
co2_kernel = (
long_term_trend_kernel + seasonal_kernel + irregularities_kernel + noise_kernel
)
co2_kernel
50**2 * RBF(length_scale=50) + 2**2 * RBF(length_scale=100) * ExpSineSquared(length_scale=1, periodicity=1) + 0.5**2 * RationalQuadratic(alpha=1, length_scale=1) + 0.1**2 * RBF(length_scale=0.1) + WhiteKernel(noise_level=0.01)
ملاءمة النموذج والاستقراء#
الآن ، نحن جاهزون لاستخدام مُنحدِر عملية غاوسية وملاءمة البيانات المتاحة. لاتباع المثال من الأدبيات ، سنطرح المتوسط من الهدف. كان بإمكاننا استخدام normalize_y=True. ومع ذلك ، فإن القيام بذلك كان سيؤدي أيضًا إلى قياس الهدف (بقسمة y على انحرافه المعياري). وبالتالي ، لكانت المعلمات الفائقة للنواة المختلفة لها معنى مختلف لأنه لم يكن من الممكن التعبير عنها بـ ppm.
from sklearn.gaussian_process import GaussianProcessRegressor
y_mean = y.mean()
gaussian_process = GaussianProcessRegressor(kernel=co2_kernel, normalize_y=False)
gaussian_process.fit(X, y - y_mean)
الآن ، سنستخدم العملية الغاوسية للتنبؤ على:
بيانات التدريب لفحص مدى الملاءمة ؛
البيانات المستقبلية لمعرفة الاستقراء الذي أجراه النموذج.
وبالتالي ، نقوم بإنشاء بيانات تركيبية من عام 1958 إلى الشهر الحالي. بالإضافة إلى ذلك ، نحتاج إلى إضافة المتوسط المطروح المحسوب أثناء التدريب.
import datetime
import numpy as np
today = datetime.datetime.now()
current_month = today.year + today.month / 12
X_test = np.linspace(start=1958, stop=current_month, num=1_000).reshape(-1, 1)
mean_y_pred, std_y_pred = gaussian_process.predict(X_test, return_std=True)
mean_y_pred += y_mean
plt.plot(X, y, color="black", linestyle="dashed", label="القياسات")
plt.plot(X_test, mean_y_pred, color="tab:blue", alpha=0.4, label="العملية الغاوسية")
plt.fill_between(
X_test.ravel(),
mean_y_pred - std_y_pred,
mean_y_pred + std_y_pred,
color="tab:blue",
alpha=0.2,
)
plt.legend()
plt.xlabel("السنة")
plt.ylabel("متوسط تركيز CO$_2$ الشهري (ppm)")
_ = plt.title(
"المتوسط الشهري لقياسات عينات الهواء\nمن مرصد مونا لوا"
)
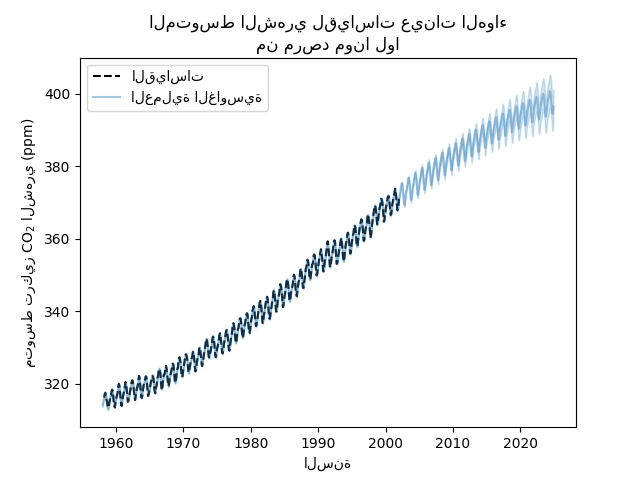
نموذجنا المجهز قادر على ملاءمة البيانات السابقة بشكل صحيح والاستقراء للسنوات القادمة بثقة.
تفسير المعلمات الفائقة للنواة#
الآن ، يمكننا إلقاء نظرة على المعلمات الفائقة للنواة.
gaussian_process.kernel_
44.8**2 * RBF(length_scale=51.6) + 2.64**2 * RBF(length_scale=91.5) * ExpSineSquared(length_scale=1.48, periodicity=1) + 0.536**2 * RationalQuadratic(alpha=2.89, length_scale=0.968) + 0.188**2 * RBF(length_scale=0.122) + WhiteKernel(noise_level=0.0367)
وبالتالي ، يتم تفسير معظم إشارة الهدف ، مع طرح المتوسط ، من خلال اتجاه تصاعدي طويل المدى لحوالي 45 جزء في المليون ومقياس طول يبلغ حوالي 52 عامًا. المكون الدوري له سعة حوالي 2.6 جزء في المليون ، ووقت انحلال يبلغ حوالي 90 عامًا ، ومقياس طول يبلغ حوالي 1.5. يشير وقت الانحلال الطويل إلى أن لدينا مكونًا قريبًا جدًا من الدورية الموسمية. الضوضاء المترابطة لها سعة حوالي 0.2 جزء في المليون مع مقياس طول يبلغ حوالي 0.12 سنة ومساهمة ضوضاء بيضاء تبلغ حوالي 0.04 جزء في المليون. وبالتالي ، فإن مستوى الضوضاء الإجمالي صغير جدًا ، مما يشير إلى أنه يمكن تفسير البيانات جيدًا بواسطة النموذج.
Total running time of the script: (0 minutes 9.082 seconds)
Related examples
قدرة انحدار العمليات الغاوسية (GPR) على تقدير مستوى ضوضاء البيانات
مقارنة انحدار kernel ridge وانحدار العمليات الغاوسية
توضيح تصنيف العملية الغاوسية (GPC) على مجموعة بيانات XOR