ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
تصنيف العملية الغاوسية (GPC) على مجموعة بيانات iris#
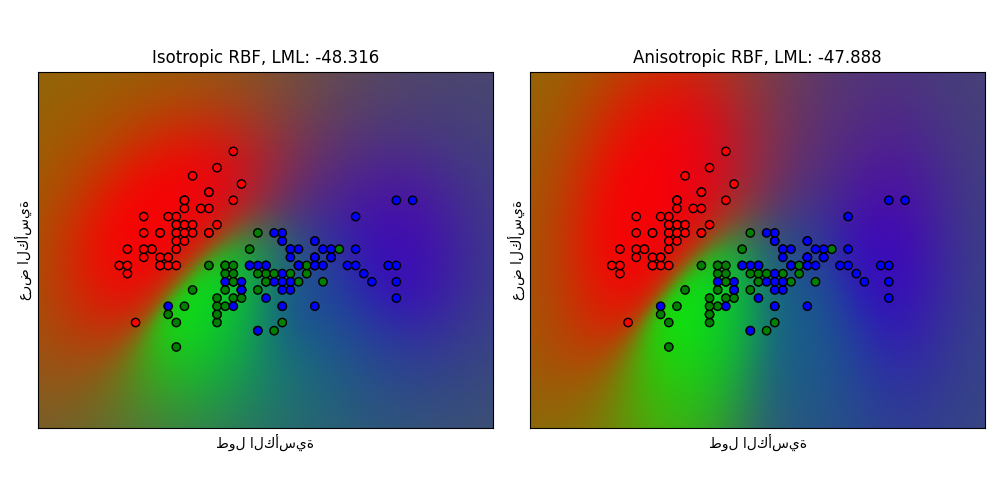
يوضح هذا المثال الاحتمال المتوقع لـ GPC لنواة RBF متناحرة وغير متناحرة على نسخة ثنائية الأبعاد لمجموعة بيانات iris. تحصل نواة RBF غير المتناحرة على احتمال هامشي لوغاريتمي أعلى قليلاً عن طريق تعيين مقاييس طول مختلفة لأبعاد الميزتين.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
# استيراد بعض البيانات للعمل بها
iris = datasets.load_iris()
X = iris.data[:, :2] # نأخذ الميزتين الأوليين فقط.
y = np.array(iris.target, dtype=int)
h = 0.02 # حجم الخطوة في الشبكة
kernel = 1.0 * RBF([1.0])
gpc_rbf_isotropic = GaussianProcessClassifier(kernel=kernel).fit(X, y)
kernel = 1.0 * RBF([1.0, 1.0])
gpc_rbf_anisotropic = GaussianProcessClassifier(kernel=kernel).fit(X, y)
# إنشاء شبكة للرسم فيها
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
titles = ["Isotropic RBF", "Anisotropic RBF"] # عناوين الرسم
plt.figure(figsize=(10, 5))
for i, clf in enumerate((gpc_rbf_isotropic, gpc_rbf_anisotropic)):
# رسم الاحتمالات المتوقعة. لذلك ، سنقوم بتعيين لون
# لكل نقطة في الشبكة [x_min, m_max]x[y_min, y_max].
plt.subplot(1, 2, i + 1)
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])
# وضع النتيجة في مخطط ألوان
Z = Z.reshape((xx.shape[0], xx.shape[1], 3))
plt.imshow(Z, extent=(x_min, x_max, y_min, y_max), origin="lower")
# رسم نقاط التدريب أيضًا
plt.scatter(X[:, 0], X[:, 1], c=np.array(["r", "g", "b"])[y], edgecolors=(0, 0, 0))
plt.xlabel("طول الكأسية") # Sepal length
plt.ylabel("عرض الكأسية") # Sepal width
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.title(
"%s, LML: %.3f" % (titles[i], clf.log_marginal_likelihood(clf.kernel_.theta))
)
plt.tight_layout()
plt.show()
Total running time of the script: (0 minutes 4.662 seconds)
Related examples
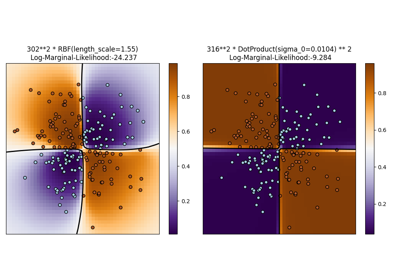
توضيح تصنيف العملية الغاوسية (GPC) على مجموعة بيانات XOR
توضيح تصنيف العملية الغاوسية (GPC) على مجموعة بيانات XOR
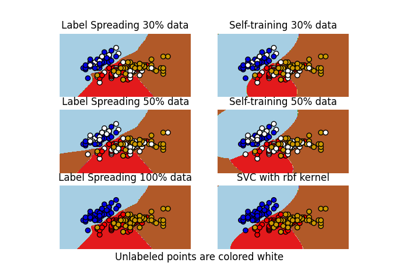
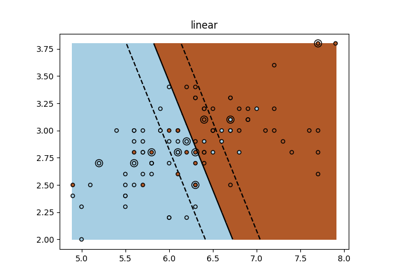
حدود القرار للمصنفات شبه المُشرفة مقابل SVM على مجموعة بيانات Iris
حدود القرار للمصنفات شبه المُشرفة مقابل SVM على مجموعة بيانات Iris
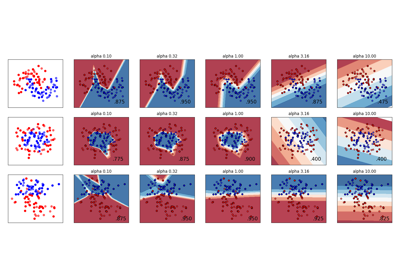
تغيير معامل التنظيم في الشبكة العصبية متعددة الطبقات
تغيير معامل التنظيم في الشبكة العصبية متعددة الطبقات