ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

انحدار العمليات الغاوسية: مثال تمهيدي أساسي#

مثال بسيط أحادي البعد للانحدار محسوب بطريقتين مختلفتين:

حالة خالية من الضوضاء
حالة ضوضاء مع مستوى ضوضاء معروف لكل نقطة بيانات

في كلتا الحالتين، يتم تقدير معلمات النواة باستخدام مبدأ الاحتمالية القصوى.

توضح الأشكال خاصية الاستيفاء لنموذج العملية الغاوسية بالإضافة إلى طبيعتها الاحتمالية في شكل فاصل ثقة بنسبة 95٪ لكل نقطة.

لاحظ أن alpha هي معلمة للتحكم في قوة تنظيم تيخونوف على مصفوفة التغاير المفترضة لنقاط التدريب.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

توليد مجموعة البيانات#

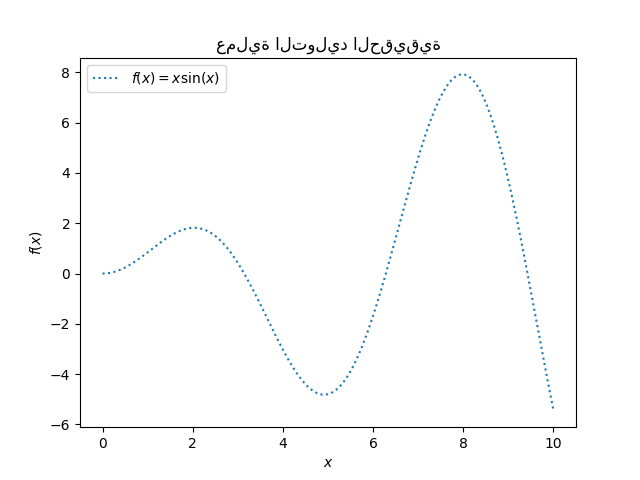
سنبدأ بتوليد مجموعة بيانات اصطناعية. يتم تعريف عملية التوليد الحقيقية على أنها \(f(x) = x \sin(x)\).

import numpy as np

X = np.linspace(start=0, stop=10, num=1_000).reshape(-1, 1)
y = np.squeeze(X * np.sin(X))

import matplotlib.pyplot as plt

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("عملية التوليد الحقيقية")

سنستخدم مجموعة البيانات هذه في التجربة التالية لتوضيح كيفية عمل انحدار العمليات الغاوسية.

مثال مع هدف خالٍ من الضوضاء#

في هذا المثال الأول، سنستخدم عملية التوليد الحقيقية دون إضافة أي ضوضاء. لتدريب انحدار العمليات الغاوسية، سنختار عينات قليلة فقط.

rng = np.random.RandomState(1)
training_indices = rng.choice(np.arange(y.size), size=6, replace=False)
X_train, y_train = X[training_indices], y[training_indices]

الآن، نقوم بملاءمة عملية غاوسية على عينات بيانات التدريب القليلة هذه. سنستخدم نواة دالة أساس شعاعية (RBF) ومعلمة ثابتة لملاءمة السعة.

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

kernel = 1 * RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e2))
gaussian_process = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)
gaussian_process.fit(X_train, y_train)
gaussian_process.kernel_

5.02**2 * RBF(length_scale=1.43)

بعد ملاءمة نموذجنا، نرى أنه قد تم تحسين المعلمات الفائقة للنواة. الآن، سنستخدم نواتنا لحساب متوسط التنبؤ لمجموعة البيانات الكاملة ورسم فاصل الثقة بنسبة 95٪.

mean_prediction, std_prediction = gaussian_process.predict(X, return_std=True)

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.scatter(X_train, y_train, label="الملاحظات")
plt.plot(X, mean_prediction, label="متوسط التنبؤ")
plt.fill_between(
    X.ravel(),
    mean_prediction - 1.96 * std_prediction,
    mean_prediction + 1.96 * std_prediction,
    alpha=0.5,
    label=r"فاصل ثقة 95%",
)
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("انحدار العمليات الغاوسية على مجموعة بيانات خالية من الضوضاء")

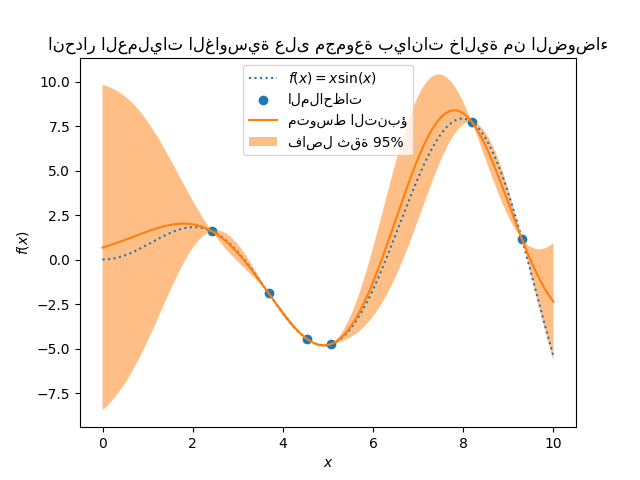
انحدار العمليات الغاوسية على مجموعة بيانات خالية من الضوضاء

نرى أنه بالنسبة للتنبؤ الذي تم إجراؤه على نقطة بيانات قريبة من نقطة بيانات من مجموعة التدريب، فإن فاصل الثقة بنسبة 95٪ له سعة صغيرة. كلما كانت العينة بعيدة عن بيانات التدريب، فإن تنبؤ نموذجنا يكون أقل دقة ويكون التنبؤ بالنموذج أقل دقة (عدم يقين أعلى).

مثال مع أهداف ضوضاء#

يمكننا تكرار تجربة مماثلة مع إضافة ضوضاء إضافية للهدف هذه المرة. سيسمح ذلك برؤية تأثير الضوضاء على النموذج الملائم.

نضيف بعض الضوضاء الغاوسية العشوائية للهدف مع انحراف معياري تعسفي.

noise_std = 0.75
y_train_noisy = y_train + rng.normal(loc=0.0, scale=noise_std, size=y_train.shape)

ننشئ نموذج عملية غاوسية مماثل. بالإضافة إلى النواة، هذه المرة، نحدد المعلمة alpha التي يمكن تفسيرها على أنها تباين ضوضاء غاوسي.

gaussian_process = GaussianProcessRegressor(
    kernel=kernel, alpha=noise_std**2, n_restarts_optimizer=9
)
gaussian_process.fit(X_train, y_train_noisy)
mean_prediction, std_prediction = gaussian_process.predict(X, return_std=True)

دعونا نرسم متوسط التنبؤ ومنطقة عدم اليقين كما كان من قبل.

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.errorbar(
    X_train,
    y_train_noisy,
    noise_std,
    linestyle="None",
    color="tab:blue",
    marker=".",
    markersize=10,
    label="الملاحظات",
)
plt.plot(X, mean_prediction, label="متوسط التنبؤ")
plt.fill_between(
    X.ravel(),
    mean_prediction - 1.96 * std_prediction,
    mean_prediction + 1.96 * std_prediction,
    color="tab:orange",
    alpha=0.5,
    label=r"فاصل ثقة 95%",
)
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("انحدار العمليات الغاوسية على مجموعة بيانات ضوضاء")

انحدار العمليات الغاوسية على مجموعة بيانات ضوضاء

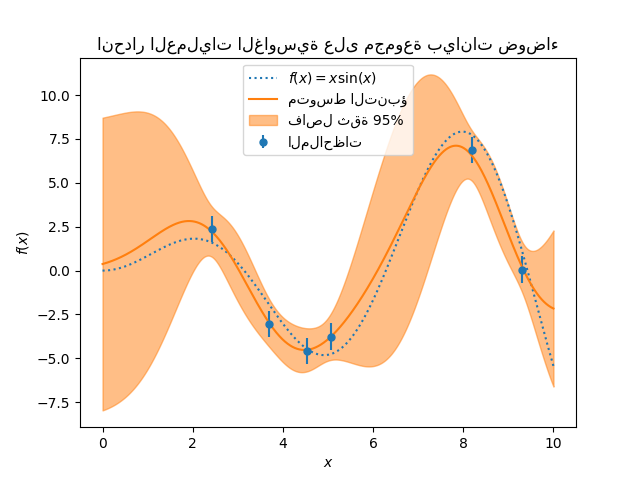
تؤثر الضوضاء على التنبؤات القريبة من عينات التدريب: يكون عدم اليقين التنبؤي بالقرب من عينات التدريب أكبر لأننا نصمم صراحة مستوى ضوضاء هدف معين بشكل مستقل عن متغير الإدخال.

Total running time of the script: (0 minutes 0.558 seconds)