ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
قدرة انحدار العمليات الغاوسية (GPR) على تقدير مستوى ضوضاء البيانات#
يوضح هذا المثال قدرة
WhiteKernel
على تقدير مستوى الضوضاء في البيانات. علاوة على ذلك، سنوضح أهمية تهيئة المعلمات الفائقة للنواة.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
توليد البيانات#
سنعمل في بيئة حيث سيحتوي X على ميزة واحدة. سننشئ دالة ستولد الهدف المراد التنبؤ به. سنضيف خيارًا لإضافة بعض الضوضاء إلى الهدف الذي تم إنشاؤه.
import numpy as np
def target_generator(X, add_noise=False):
target = 0.5 + np.sin(3 * X)
if add_noise:
rng = np.random.RandomState(1)
target += rng.normal(0, 0.3, size=target.shape)
return target.squeeze()
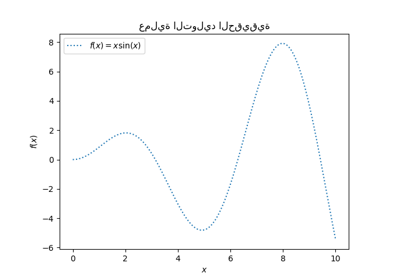
لنلقِ نظرة على مُولد الأهداف حيث لن نضيف أي ضوضاء لمراقبة الإشارة التي نرغب في التنبؤ بها.
X = np.linspace(0, 5, num=80).reshape(-1, 1)
y = target_generator(X, add_noise=False)
import matplotlib.pyplot as plt
plt.plot(X, y, label="الإشارة المتوقعة")
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")
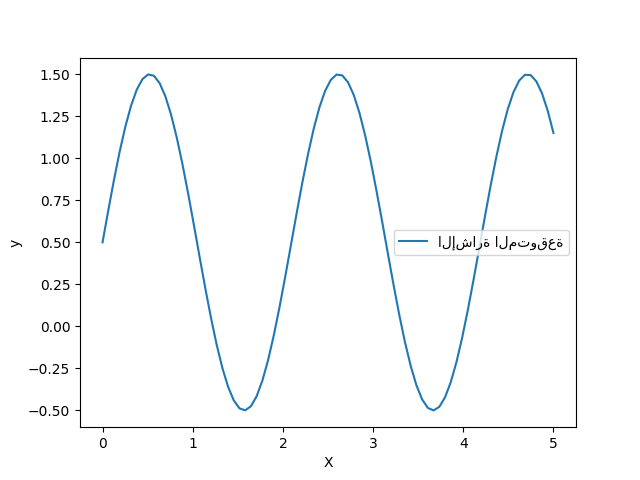
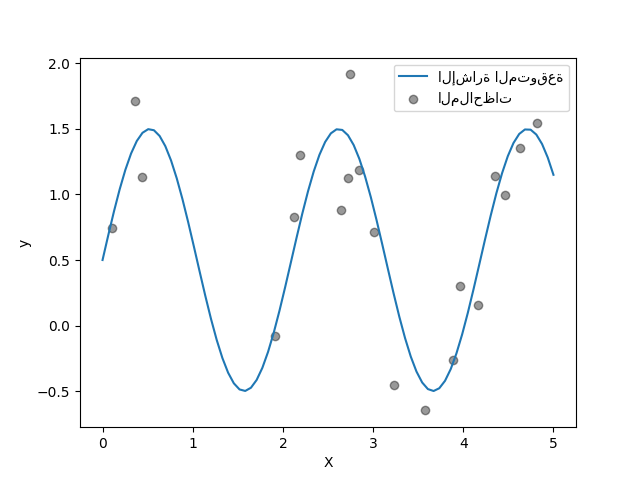
يقوم الهدف بتحويل المدخلات X باستخدام دالة الجيب. الآن، سنقوم بإنشاء بعض عينات التدريب المزعجة. لتوضيح مستوى الضوضاء، سنرسم الإشارة الحقيقية مع عينات التدريب المزعجة.
rng = np.random.RandomState(0)
X_train = rng.uniform(0, 5, size=20).reshape(-1, 1)
y_train = target_generator(X_train, add_noise=True)
plt.plot(X, y, label="الإشارة المتوقعة")
plt.scatter(
x=X_train[:, 0],
y=y_train,
color="black",
alpha=0.4,
label="الملاحظات",
)
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")
تحسين المعلمات الفائقة للنواة في GPR#
الآن، سنقوم بإنشاء
GaussianProcessRegressor
باستخدام نواة مضافة تجمع بين نواتي
RBF
و
WhiteKernel.
النواة WhiteKernel هي نواة ستكون قادرة على تقدير كمية الضوضاء الموجودة في البيانات بينما ستعمل النواة RBF على ملاءمة اللاخطية بين البيانات والهدف.
ومع ذلك، سنوضح أن مساحة المعلمات الفائقة تحتوي على العديد من الحدود الدنيا المحلية. وهذا سيبرز أهمية القيم الأولية للمعلمات الفائقة.
سنقوم بإنشاء نموذج باستخدام نواة ذات مستوى ضوضاء عالٍ ومقياس طول كبير، مما سيفسر جميع الاختلافات في البيانات بالضوضاء.
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
noise_level=1, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)
plt.plot(X, y, label="الإشارة المتوقعة")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="الملاحظات")
plt.errorbar(X, y_mean, y_std, label="المتوسط اللاحق ± الانحراف المعياري")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
(
f"القيمة الأولية: {kernel}\nالقيمة المثلى: {gpr.kernel_}\nاحتمالية الهامش اللوغاريتمي: "
f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
),
fontsize=8,
)
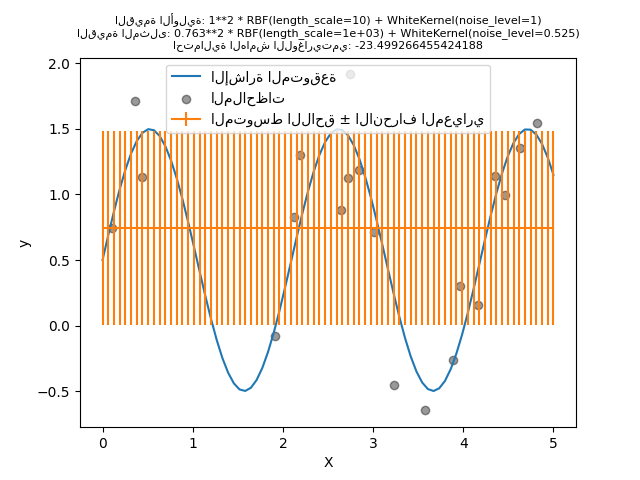
نرى أن النواة المثلى التي تم العثور عليها لا تزال ذات مستوى ضوضاء عالٍ ومقياس طول أكبر. يصل مقياس الطول إلى الحد الأقصى المسموح به لهذا المعلم وقد تلقينا تحذيرًا نتيجة لذلك.
والأهم من ذلك، نلاحظ أن النموذج لا يقدم تنبؤات مفيدة: يبدو أن التنبؤ المتوسط ثابت: فهو لا يتبع الإشارة المتوقعة الخالية من الضوضاء.
الآن، سنقوم بتهيئة RBF بقيمة أولية أكبر لـ length_scale و WhiteKernel بمستوى ضوضاء أولي أصغر مع الحفاظ على حدود المعلمات دون تغيير.
kernel = 1.0 * RBF(length_scale=1e-1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
noise_level=1e-2, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)
plt.plot(X, y, label="الإشارة المتوقعة")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="الملاحظات")
plt.errorbar(X, y_mean, y_std, label="المتوسط اللاحق ± الانحراف المعياري")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
(
f"القيمة الأولية: {kernel}\nالقيمة المثلى: {gpr.kernel_}\nاحتمالية الهامش اللوغاريتمي: "
f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
),
fontsize=8,
)
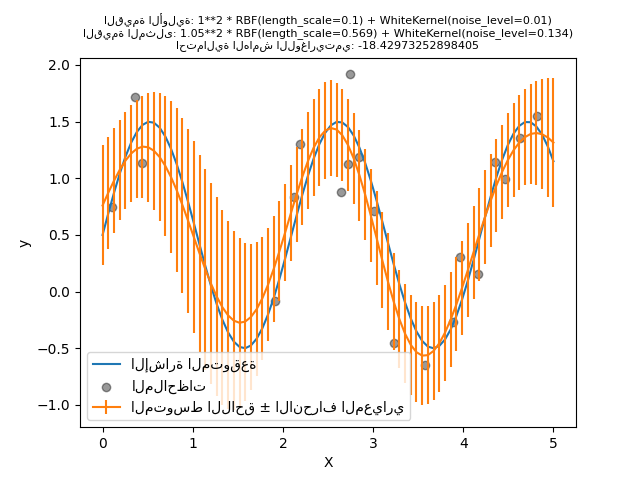
أولاً، نرى أن تنبؤات النموذج أكثر دقة من تنبؤات النموذج السابق: هذا النموذج الجديد قادر على تقدير العلاقة الدالية الخالية من الضوضاء.
بالنظر إلى المعلمات الفائقة للنواة، نرى أن أفضل توليفة تم العثور عليها تتميز بمستوى ضوضاء أقل ومقياس طول أقصر من النموذج الأول.
يمكننا فحص احتمالية الهامش اللوغاريتمي (LML) لـ GaussianProcessRegressor لمعلمات فائقة مختلفة للحصول على فكرة عن الحدود الدنيا المحلية.
from matplotlib.colors import LogNorm
length_scale = np.logspace(-2, 4, num=80)
noise_level = np.logspace(-2, 1, num=80)
length_scale_grid, noise_level_grid = np.meshgrid(length_scale, noise_level)
log_marginal_likelihood = [
gpr.log_marginal_likelihood(theta=np.log([0.36, scale, noise]))
for scale, noise in zip(length_scale_grid.ravel(), noise_level_grid.ravel())
]
log_marginal_likelihood = np.reshape(log_marginal_likelihood, noise_level_grid.shape)
vmin, vmax = (-log_marginal_likelihood).min(), 50
level = np.around(np.logspace(np.log10(vmin), np.log10(vmax), num=20), decimals=1)
plt.contour(
length_scale_grid,
noise_level_grid,
-log_marginal_likelihood,
levels=level,
norm=LogNorm(vmin=vmin, vmax=vmax),
)
plt.colorbar()
plt.xscale("log")
plt.yscale("log")
plt.xlabel("مقياس الطول")
plt.ylabel("مستوى الضوضاء")
plt.title("احتمالية الهامش اللوغاريتمي")
plt.show()
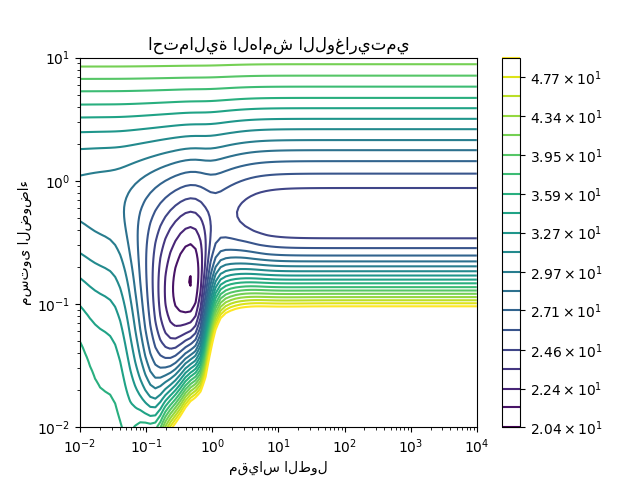
نرى أن هناك حدين أدنى محليين يتوافقان مع توليفة المعلمات الفائقة التي تم العثور عليها سابقًا. اعتمادًا على القيم الأولية للمعلمات الفائقة، قد يتقارب التحسين القائم على التدرج أو لا يتقارب مع أفضل نموذج. لذلك من المهم تكرار التحسين عدة مرات لتهيئات مختلفة. يمكن القيام بذلك عن طريق تعيين المعلمة n_restarts_optimizer للفئة GaussianProcessRegressor.
دعونا نحاول مرة أخرى ملاءمة نموذجنا بالقيم الأولية السيئة ولكن هذه المرة مع 10 عمليات إعادة تشغيل عشوائية.
kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
noise_level=1, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(
kernel=kernel, alpha=0.0, n_restarts_optimizer=10, random_state=0
)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)
plt.plot(X, y, label="الإشارة المتوقعة")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="الملاحظات")
plt.errorbar(X, y_mean, y_std, label="المتوسط اللاحق ± الانحراف المعياري")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
(
f"القيمة الأولية: {kernel}\nالقيمة المثلى: {gpr.kernel_}\nاحتمالية الهامش اللوغاريتمي: "
f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
),
fontsize=8,
)
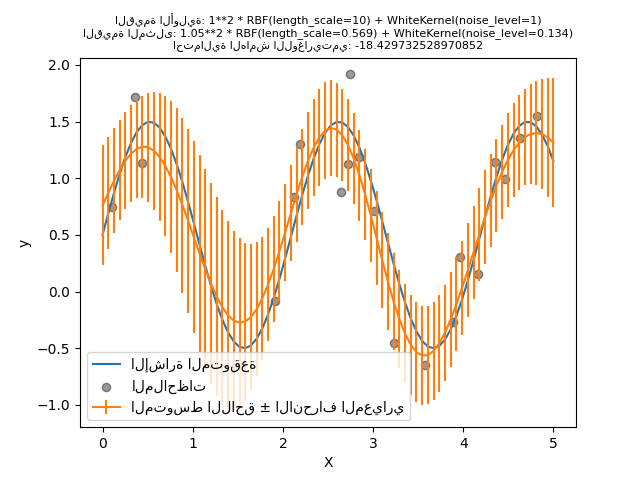
كما كنا نأمل، تسمح عمليات إعادة التشغيل العشوائية للتحسين بالعثور على أفضل مجموعة من المعلمات الفائقة على الرغم من القيم الأولية السيئة.
Total running time of the script: (0 minutes 6.884 seconds)
Related examples
توضيح العملية الغاوسية المسبقة واللاحقة لنوى مختلفة
التنبؤ بمستوى ثاني أكسيد الكربون في مجموعة بيانات Mona Loa باستخدام انحدار العملية الغاوسية (GPR)
مقارنة انحدار kernel ridge وانحدار العمليات الغاوسية