ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

استخدام KBinsDiscretizer لتقسيم الخصائص المستمرة#

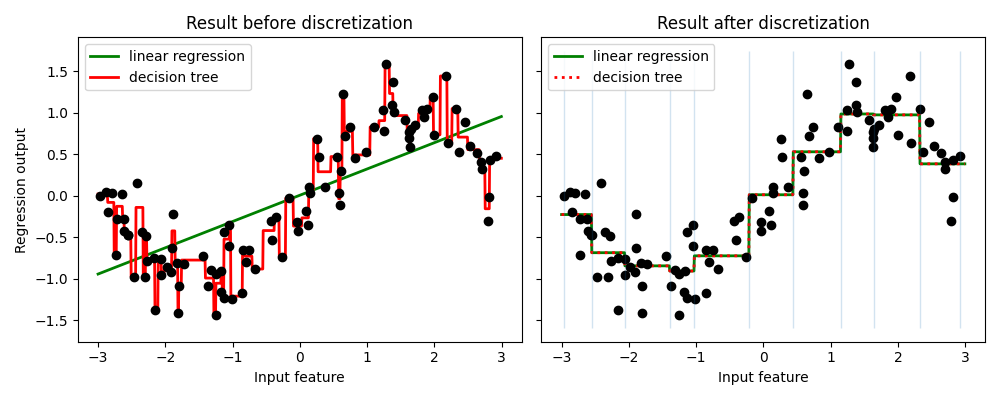
يقارن المثال نتيجة التنبؤ بالانحدار الخطي (النموذج الخطي) وشجرة القرار (النموذج القائم على الشجرة) مع وبدون تقسيم الخصائص ذات القيم الحقيقية.

كما هو موضح في النتيجة قبل التقسيم، فإن النموذج الخطي سريع البناء وسهل التفسير نسبيًا، ولكنه لا يمكنه سوى نمذجة العلاقات الخطية، في حين يمكن لشجرة القرار بناء نموذج أكثر تعقيدًا بكثير للبيانات. إحدى طرق جعل النموذج الخطي أكثر قوة على البيانات المستمرة هي استخدام التقسيم (المعروف أيضًا باسم التصنيف). في المثال، نقوم بتقسيم الخاصية ونقوم بترميز البيانات المحولة بطريقة "one-hot". لاحظ أنه إذا لم تكن الفئات واسعة بشكل معقول، فسيبدو أن هناك زيادة كبيرة في خطر الإفراط في التخصيص، لذلك يجب عادةً ضبط معلمات التقسيم تحت التحقق المتقاطع.

بعد التقسيم، يقوم الانحدار الخطي وشجرة القرار بالتنبؤ بنفس الطريقة تمامًا. حيث أن الخصائص ثابتة داخل كل فئة، يجب على أي نموذج أن يتنبأ بنفس القيمة لجميع النقاط داخل الفئة. مقارنة بالنتيجة قبل التقسيم، يصبح الانحدار الخطي أكثر مرونة بكثير بينما تصبح شجرة القرار أقل مرونة بكثير. لاحظ أن تقسيم الخصائص بشكل عام ليس له تأثير مفيد على النماذج القائمة على الشجرة، حيث يمكن لهذه النماذج أن تتعلم تقسيم البيانات في أي مكان.

Result before discretization, Result after discretization

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor

# إنشاء مجموعة البيانات
rnd = np.random.RandomState(42)
X = rnd.uniform(-3, 3, size=100)
y = np.sin(X) + rnd.normal(size=len(X)) / 3
X = X.reshape(-1, 1)

# تحويل مجموعة البيانات باستخدام KBinsDiscretizer
enc = KBinsDiscretizer(n_bins=10, encode="onehot")
X_binned = enc.fit_transform(X)

# التنبؤ بمجموعة البيانات الأصلية
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(10, 4))
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
reg = LinearRegression().fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color="green", label="linear regression")
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color="red", label="decision tree")
ax1.plot(X[:, 0], y, "o", c="k")
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")

# التنبؤ بمجموعة البيانات المحولة
line_binned = enc.transform(line)
reg = LinearRegression().fit(X_binned, y)
ax2.plot(
    line,
    reg.predict(line_binned),
    linewidth=2,
    color="green",
    linestyle="-",
    label="linear regression",
)
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X_binned, y)
ax2.plot(
    line,
    reg.predict(line_binned),
    linewidth=2,
    color="red",
    linestyle=":",
    label="decision tree",
)
ax2.plot(X[:, 0], y, "o", c="k")
ax2.vlines(enc.bin_edges_[0], *plt.gca().get_ylim(), linewidth=1, alpha=0.2)
ax2.legend(loc="best")
ax2.set_xlabel("Input feature")
ax2.set_title("Result after discretization")

plt.tight_layout()
plt.show()