ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

التكامل متعدد الحدود والتقسيم#

يوضح هذا المثال كيفية تقريب دالة باستخدام متعددات الحدود حتى الدرجة degree باستخدام الانحدار المحدب. نعرض طريقتين مختلفتين نظرًا لـ n_samples من النقاط 1d x_i:

PolynomialFeatures يولد جميع متعددات الحدود حتى degree. وهذا يعطينا ما يسمى مصفوفة Vandermonde مع n_samples صفوف و degree + 1 أعمدة:
```
[[1, x_0, x_0 ** 2, x_0 ** 3, ..., x_0 ** degree],
 [1, x_1, x_1 ** 2, x_1 ** 3, ..., x_1 ** degree],
 ...]
```
بديهيًا، يمكن تفسير هذه المصفوفة على أنها مصفوفة من الميزات الزائفة (النقاط المرتفعة إلى بعض القوة). المصفوفة تشبه (ولكنها مختلفة عن) المصفوفة الناتجة عن نواة متعددة الحدود.
SplineTransformer يولد وظائف أساس B-spline. وظيفة أساس B-spline هي دالة متعددة الحدود القطعية من الدرجة degree التي لا تساوي الصفر إلا بين degree+1 العقد المتتالية. نظرًا لعدد العقد n_knots، ينتج عن ذلك مصفوفة من n_samples صفوف و n_knots + degree - 1 أعمدة:
```
[[basis_1(x_0), basis_2(x_0), ...],
 [basis_1(x_1), basis_2(x_1), ...],
 ...]
```

يوضح هذا المثال أن هذين المحولين مناسبان جيدًا لنمذجة التأثيرات غير الخطية بنموذج خطي، باستخدام خط أنابيب لإضافة ميزات غير خطية. توسع طرق النواة هذه الفكرة ويمكنها استنتاج مساحات ميزات عالية جدًا (حتى لا نهائية) الأبعاد.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, SplineTransformer

نبدأ بتعريف دالة نعتزم تقريبها وإعداد رسمها.

def f(x):
    """دالة ليتم تقريبها بواسطة التكامل متعدد الحدود."""
    return x * np.sin(x)


# النطاق الكامل الذي نريد رسمه
x_plot = np.linspace(-1, 11, 100)

لجعلها مثيرة للاهتمام، نقدم فقط مجموعة فرعية صغيرة من النقاط للتدريب.

x_train = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
x_train = np.sort(rng.choice(x_train, size=20, replace=False))
y_train = f(x_train)

# إنشاء إصدارات مصفوفة 2D من هذه المصفوفات لإطعام المحولات
X_train = x_train[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]

الآن نحن مستعدون لإنشاء ميزات متعددة الحدود وتقسيمها، والتدريب على النقاط التدريبية وإظهار مدى جودة تقريبها.

# رسم الدالة
lw = 2
fig, ax = plt.subplots()
ax.set_prop_cycle(
    color=["black", "teal", "yellowgreen", "gold", "darkorange", "tomato"]
)
ax.plot(x_plot, f(x_plot), linewidth=lw, label="ground truth")

# رسم نقاط التدريب
ax.scatter(x_train, y_train, label="training points")

# الميزات متعددة الحدود
for degree in [3, 4, 5]:
    model = make_pipeline(PolynomialFeatures(degree), Ridge(alpha=1e-3))
    model.fit(X_train, y_train)
    y_plot = model.predict(X_plot)
    ax.plot(x_plot, y_plot, label=f"degree {degree}")

# B-spline مع 4 + 3 - 1 = 6 وظائف أساس
model = make_pipeline(SplineTransformer(n_knots=4, degree=3), Ridge(alpha=1e-3))
model.fit(X_train, y_train)

y_plot = model.predict(X_plot)
ax.plot(x_plot, y_plot, label="B-spline")
ax.legend(loc="lower center")
ax.set_ylim(-20, 10)
plt.show()

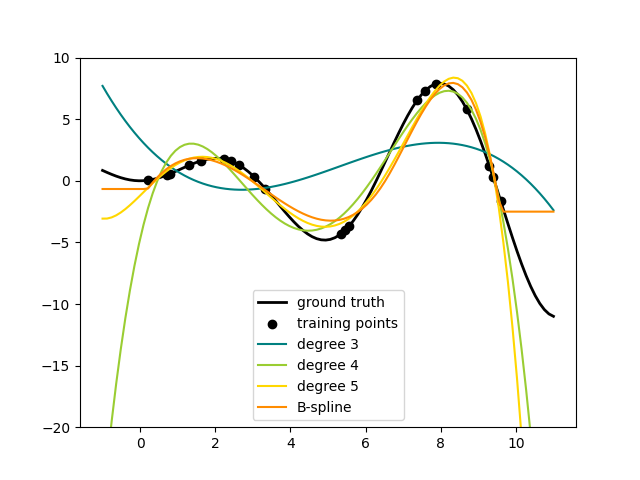
هذا يظهر بوضوح أن متعددات الحدود ذات الدرجة الأعلى يمكنها ملاءمة البيانات بشكل أفضل. ولكن في نفس الوقت، يمكن للقوى العالية جدًا أن تظهر سلوكًا متذبذبًا غير مرغوب فيه وهي خطيرة بشكل خاص للاستقراء خارج نطاق البيانات المناسب. هذه ميزة B-splines. عادة ما تناسب البيانات جيدًا مثل متعددات الحدود ولها سلوك لطيف جدًا وسلس. لديهم أيضًا خيارات جيدة للتحكم في الاستقراء، والذي يظل افتراضيًا مستمرًا بثابت. لاحظ أنه في معظم الأحيان، تفضل زيادة عدد العقد ولكن الحفاظ على degree=3.

من أجل إعطاء المزيد من الأفكار حول قواعد الميزات المولدة، نرسم جميع أعمدة كل من المحولات بشكل منفصل.

fig, axes = plt.subplots(ncols=2, figsize=(16, 5))
pft = PolynomialFeatures(degree=3).fit(X_train)
axes[0].plot(x_plot, pft.transform(X_plot))
axes[0].legend(axes[0].lines, [f"degree {n}" for n in range(4)])
axes[0].set_title("PolynomialFeatures")

splt = SplineTransformer(n_knots=4, degree=3).fit(X_train)
axes[1].plot(x_plot, splt.transform(X_plot))
axes[1].legend(axes[1].lines, [f"spline {n}" for n in range(6)])
axes[1].set_title("SplineTransformer")

# رسم العقد من spline
knots = splt.bsplines_[0].t
axes[1].vlines(knots[3:-3], ymin=0, ymax=0.8, linestyles="dashed")
plt.show()

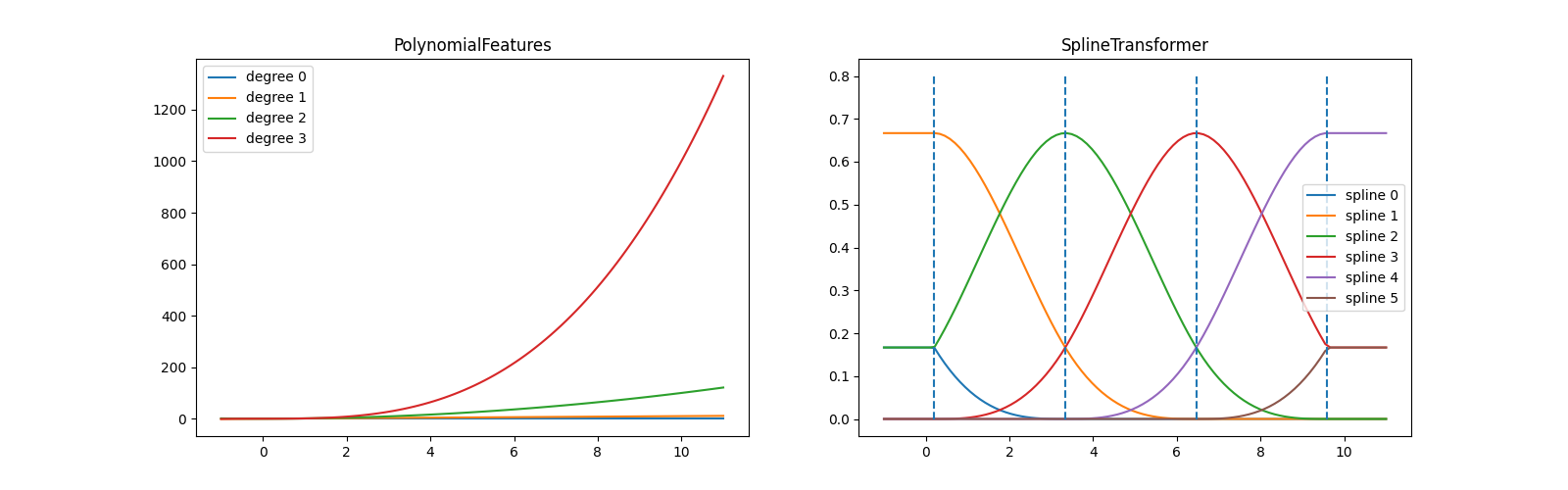
في الرسم البياني الأيسر، نتعرف على الخطوط المقابلة للمتعددات الحدود البسيطة من x**0 إلى x**3. في الشكل الأيمن، نرى ست وظائف أساس B-spline من degree=3 وأيضًا مواضع العقد الأربعة التي تم اختيارها أثناء fit. لاحظ أنه هناك عدد degree من العقد الإضافية لكل من اليسار واليمين من الفاصل الزمني المناسب. هذه هي لأسباب فنية، لذلك نحن نمتنع عن إظهارها. لكل وظيفة أساس دعم محلي ويستمر كقيمة ثابتة خارج النطاق المناسب. يمكن تغيير هذا السلوك الاستقرائي بواسطة الحجة extrapolation.

تقسيم دوري#

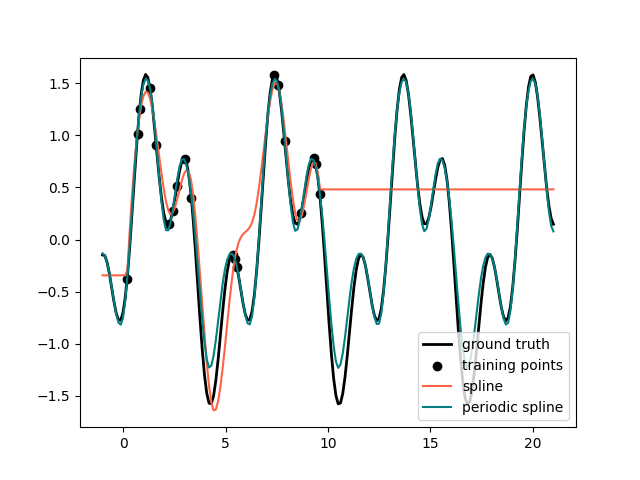
في المثال السابق، رأينا قيود متعددات الحدود والتقسيمات للاستقراء خارج نطاق الملاحظات التدريبية. في بعض الإعدادات، على سبيل المثال، مع التأثيرات الموسمية، نتوقع استمرار دوري للإشارة الأساسية. يمكن نمذجة مثل هذه التأثيرات باستخدام تقسيم دوري، التي لها قيمة دالة متساوية ومشتقات متساوية في العقدة الأولى والأخيرة. في الحالة التالية نعرض كيف توفر التقسيمات الدورية ملاءمة أفضل داخل وخارج نطاق بيانات التدريب نظرًا للمعلومات الإضافية الدورية. فترة التقسيمات هي المسافة بين العقدة الأولى والأخيرة، والتي نحددها يدويًا.

يمكن أن تكون التقسيمات الدورية مفيدة أيضًا للميزات الدورية بشكل طبيعي (مثل يوم السنة)، حيث تمنع السلاسة في العقد الحدودية قفزة في القيم المحولة (على سبيل المثال، من 31 ديسمبر إلى 1 يناير). بالنسبة لهذه الميزات الدورية بشكل طبيعي أو بشكل عام الميزات التي تكون الفترة معروفة، فمن المستحسن تمرير هذه المعلومات صراحةً إلى SplineTransformer عن طريق تعيين العقد يدويًا.

def g(x):
    """دالة ليتم تقريبها بواسطة التكامل التقسيمي الدوري."""
    return np.sin(x) - 0.7 * np.cos(x * 3)


y_train = g(x_train)

# تمديد بيانات الاختبار إلى المستقبل:
x_plot_ext = np.linspace(-1, 21, 200)
X_plot_ext = x_plot_ext[:, np.newaxis]

lw = 2
fig, ax = plt.subplots()
ax.set_prop_cycle(color=["black", "tomato", "teal"])
ax.plot(x_plot_ext, g(x_plot_ext), linewidth=lw, label="ground truth")
ax.scatter(x_train, y_train, label="training points")

for transformer, label in [
    (SplineTransformer(degree=3, n_knots=10), "spline"),
    (
        SplineTransformer(
            degree=3,
            knots=np.linspace(0, 2 * np.pi, 10)[:, None],
            extrapolation="periodic",
        ),
        "periodic spline",
    ),
]:
    model = make_pipeline(transformer, Ridge(alpha=1e-3))
    model.fit(X_train, y_train)
    y_plot_ext = model.predict(X_plot_ext)
    ax.plot(x_plot_ext, y_plot_ext, label=label)

ax.legend()
fig.show()

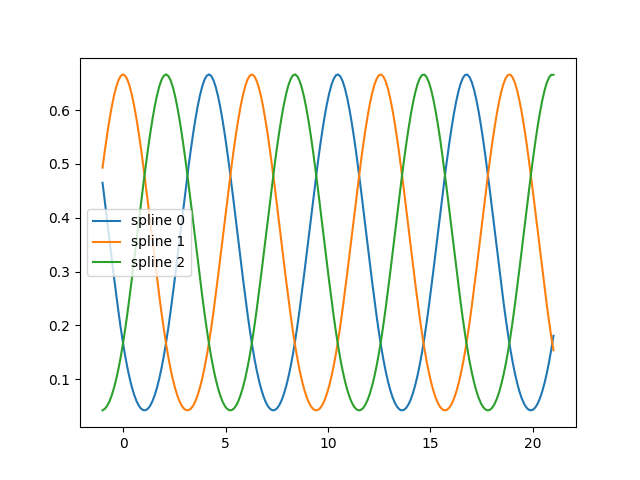
fig, ax = plt.subplots()
knots = np.linspace(0, 2 * np.pi, 4)
splt = SplineTransformer(knots=knots[:, None], degree=3, extrapolation="periodic").fit(
    X_train
)
ax.plot(x_plot_ext, splt.transform(X_plot_ext))
ax.legend(ax.lines, [f"spline {n}" for n in range(3)])
plt.show()