ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
مقارنة تأثير المقياس المختلف على البيانات مع القيم الشاذة#
تتميز الخاصية 0 (متوسط الدخل في الكتلة) والخاصية 5 (متوسط شغل المنزل) في California Housing dataset بمقاييس مختلفة جداً وتحتوي على بعض القيم الشاذة الكبيرة جدًا. تؤدي هاتان الخاصيتان إلى صعوبات في تصور البيانات, والأهم من ذلك, يمكن أن تتدهور الأداء التنبؤي للعديد من خوارزميات التعلم الآلي. يمكن أن تؤدي البيانات غير المقاسة أيضًا إلى إبطاء أو حتى منع تقارب العديد من المقدرات القائمة على التدرج.
في الواقع, تم تصميم العديد من المقدرات بافتراض أن كل ميزة تأخذ القيم القريبة من الصفر أو, بشكل أكثر أهمية, أن جميع الميزات تختلف على نطاقات قابلة للمقارنة. على وجه الخصوص, غالبًا ما تفترض المقدرات المترية والقائمة على التدرج بيانات تقريبية قياسية (ميزات مركزية مع تباينات الوحدة). الاستثناء الملحوظ هو المقدرات القائمة على شجرة القرار التي تكون قوية للتدرج التعسفي للبيانات.
يستخدم هذا المثال مقاييس ودوال تحويل وتطبيع مختلفة لجلب البيانات ضمن نطاق محدد مسبقًا.
المقاييس هي محولات خطية (أو أكثر دقة محولات أفينية) وتختلف عن بعضها البعض في الطريقة التي تقدر بها المعلمات المستخدمة لنقل وتوسيع كل ميزة.
QuantileTransformer يوفر تحولات غير خطية
في المسافات
بين القيم الشاذة الهامشية والقيم الداخلية يتم تقليصها.
PowerTransformer يوفر
تحولات غير خطية يتم فيها رسم البيانات إلى توزيع طبيعي لتثبيت
التباين وتقليل الانحراف.
على عكس التحولات السابقة, يشير التطبيع إلى تحويل لكل عينة بدلاً من تحويل لكل ميزة.
قد يكون الكود التالي طويلاً بعض الشيء, لذا لا تتردد في الانتقال مباشرةً إلى تحليل النتائج_.
# المؤلفون: مطوري سكايلرن
# معرف SPDX-License: BSD-3-Clause
import matplotlib as mpl
import numpy as np
from matplotlib import cm
from matplotlib import pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import (
MaxAbsScaler,
MinMaxScaler,
Normalizer,
PowerTransformer,
QuantileTransformer,
RobustScaler,
StandardScaler,
minmax_scale,
)
dataset = fetch_california_housing()
X_full, y_full = dataset.data, dataset.target
feature_names = dataset.feature_names
feature_mapping = {
"MedInc": "Median income in block",
"HouseAge": "Median house age in block",
"AveRooms": "Average number of rooms",
"AveBedrms": "Average number of bedrooms",
"Population": "Block population",
"AveOccup": "Average house occupancy",
"Latitude": "House block latitude",
"Longitude": "House block longitude",
}
# خذ فقط ميزتين لجعل التصوير أسهل
# تحتوي ميزة MedInc على توزيع طويل الذيل.
# تحتوي الميزة AveOccup على عدد قليل من القيم الشاذة ولكنها كبيرة جدًا.
features = ["MedInc", "AveOccup"]
features_idx = [feature_names.index(feature) for feature in features]
X = X_full[:, features_idx]
distributions = [
("البيانات غير المقاسة", X),
("البيانات بعد التوسيع القياسي", StandardScaler().fit_transform(X)),
("البيانات بعد التوسيع من الحد الأدنى إلى الحد الأقصى", MinMaxScaler().fit_transform(X)),
("البيانات بعد التوسيع من الحد الأقصى إلى الحد الأدنى", MaxAbsScaler().fit_transform(X)),
(
"البيانات بعد التوسيع المتين",
RobustScaler(quantile_range=(25, 75)).fit_transform(X),
),
(
"البيانات بعد التحول بالقوة (Yeo-Johnson)",
PowerTransformer(method="yeo-johnson").fit_transform(X),
),
(
"البيانات بعد التحول بالقوة (Box-Cox)",
PowerTransformer(method="box-cox").fit_transform(X),
),
(
"البيانات بعد التحول الكمي (توزيع احتمالي موحد)",
QuantileTransformer(
output_distribution="uniform", random_state=42
).fit_transform(X),
),
(
"البيانات بعد التحول الكمي (توزيع احتمالي طبيعي)",
QuantileTransformer(
output_distribution="normal", random_state=42
).fit_transform(X),
),
("البيانات بعد التطبيع العيني L2", Normalizer().fit_transform(X)),
]
# قم بتوسيع الإخراج بين 0 و 1 لشريط الألوان
y = minmax_scale(y_full)
# البلازما غير موجودة في ماتبلوتليب <1.5
cmap = getattr(cm, "plasma_r", cm.hot_r)
def create_axes(title, figsize=(16, 6)):
fig = plt.figure(figsize=figsize)
fig.suptitle(title)
# تحديد المحور للرسم الأول
left, width = 0.1, 0.22
bottom, height = 0.1, 0.7
bottom_h = height + 0.15
left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.1]
rect_histy = [left_h, bottom, 0.05, height]
ax_scatter = plt.axes(rect_scatter)
ax_histx = plt.axes(rect_histx)
ax_histy = plt.axes(rect_histy)
# تحديد المحور للرسم المكبر
left = width + left + 0.2
left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.1]
rect_histy = [left_h, bottom, 0.05, height]
ax_scatter_zoom = plt.axes(rect_scatter)
ax_histx_zoom = plt.axes(rect_histx)
ax_histy_zoom = plt.axes(rect_histy)
# تحديد المحور لشريط الألوان
left, width = width + left + 0.13, 0.01
rect_colorbar = [left, bottom, width, height]
ax_colorbar = plt.axes(rect_colorbar)
return (
(ax_scatter, ax_histy, ax_histx),
(ax_scatter_zoom, ax_histy_zoom, ax_histx_zoom),
ax_colorbar,
)
def plot_distribution(axes, X, y, hist_nbins=50, title="", x0_label="", x1_label=""):
ax, hist_X1, hist_X0 = axes
ax.set_title(title)
ax.set_xlabel(x0_label)
ax.set_ylabel(x1_label)
# رسم التبعثر
colors = cmap(y)
ax.scatter(X[:, 0], X[:, 1], alpha=0.5, marker="o", s=5, lw=0, c=colors)
# إزالة العمود الفقري العلوي والأيمن من أجل الجماليات
# إجراء تخطيط محور لطيف
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
ax.spines["left"].set_position(("outward", 10))
ax.spines["bottom"].set_position(("outward", 10))
# رسم بياني للتاريخ X1 (الميزة 5)
hist_X1.set_ylim(ax.get_ylim())
hist_X1.hist(
X[:, 1], bins=hist_nbins, orientation="horizontal", color="grey", ec="grey"
)
hist_X1.axis("off")
# رسم بياني للتاريخ X0 (الميزة 0)
hist_X0.set_xlim(ax.get_xlim())
hist_X0.hist(
X[:, 0], bins=hist_nbins, orientation="vertical", color="grey", ec="grey"
)
hist_X0.axis("off")
سيتم عرض رسمين لكل مقياس/مطبق/محول. سيظهر الرسم الأيسر رسمًا نقطيًا لمجموعة البيانات الكاملة بينما سيستبعد الرسم الأيمن القيم المتطرفة بالنظر فقط إلى 99% من مجموعة البيانات, واستبعاد القيم الشاذة الهامشية. بالإضافة إلى ذلك, سيتم عرض التوزيعات الهامشية لكل ميزة على جانبي الرسم البياني.
def make_plot(item_idx):
title, X = distributions[item_idx]
ax_zoom_out, ax_zoom_in, ax_colorbar = create_axes(title)
axarr = (ax_zoom_out, ax_zoom_in)
plot_distribution(
axarr[0],
X,
y,
hist_nbins=200,
x0_label=feature_mapping[features[0]],
x1_label=feature_mapping[features[1]],
title="Full data",
)
# التكبير
zoom_in_percentile_range = (0, 99)
cutoffs_X0 = np.percentile(X[:, 0], zoom_in_percentile_range)
cutoffs_X1 = np.percentile(X[:, 1], zoom_in_percentile_range)
non_outliers_mask = np.all(X > [cutoffs_X0[0], cutoffs_X1[0]], axis=1) & np.all(
X < [cutoffs_X0[1], cutoffs_X1[1]], axis=1
)
plot_distribution(
axarr[1],
X[non_outliers_mask],
y[non_outliers_mask],
hist_nbins=50,
x0_label=feature_mapping[features[0]],
x1_label=feature_mapping[features[1]],
title="Zoom-in",
)
norm = mpl.colors.Normalize(y_full.min(), y_full.max())
mpl.colorbar.ColorbarBase(
ax_colorbar,
cmap=cmap,
norm=norm,
orientation="vertical",
label="Color mapping for values of y",
)
البيانات الأصلية#
يتم رسم كل تحول لإظهار ميزتين محولتين, مع عرض الرسم الأيسر لمجموعة البيانات الكاملة, واليمين مكبر لإظهار مجموعة البيانات بدون القيم الشاذة الهامشية. يتم ضغط الغالبية العظمى من العينات إلى نطاق محدد, [0, 10] للدخل المتوسط و [0, 6] لشغل المنزل المتوسط. لاحظ أنه هناك بعض القيم الشاذة الهامشية (بعض الكتل بها متوسط شغل أكثر من 1200). لذلك, يمكن أن يكون معالجة محددة مفيدًا جدًا اعتمادًا على التطبيق. في ما يلي, نقدم بعض الأفكار وسلوكيات أساليب المعالجة المسبقة هذه في وجود القيم الشاذة الهامشية.
make_plot(0)
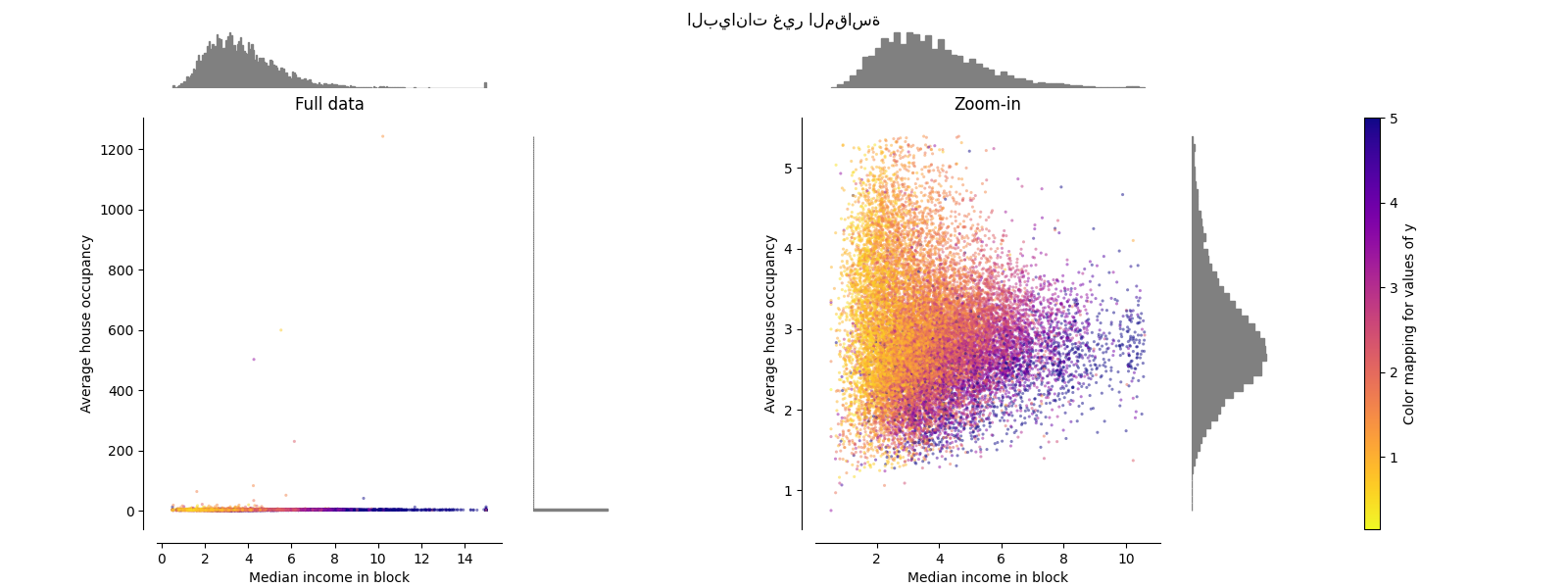
StandardScaler#
StandardScaler يزيل المتوسط ويوسع
البيانات إلى تباين الوحدة. يقلل التوسيع من نطاق قيم الميزة كما هو موضح في
الرسم الأيسر أدناه.
ومع ذلك, يكون للقيم الشاذة تأثير عند حساب المتوسط التجريبي
والانحراف المعياري. لاحظ على وجه الخصوص أنه لأن القيم الشاذة في كل
ميزة لها أحجام مختلفة, فإن انتشار البيانات المحولة على
كل ميزة مختلفة جدًا: تقع معظم البيانات في النطاق [-2, 4] للميزة
الدخل المتوسط المحولة في حين يتم ضغط نفس البيانات في
النطاق الأصغر [-0.2, 0.2] لشغل المنزل المتوسط المحول.
StandardScaler لذلك لا يمكن أن يضمن
نطاقات ميزات متوازنة في
وجود القيم الشاذة.
make_plot(1)
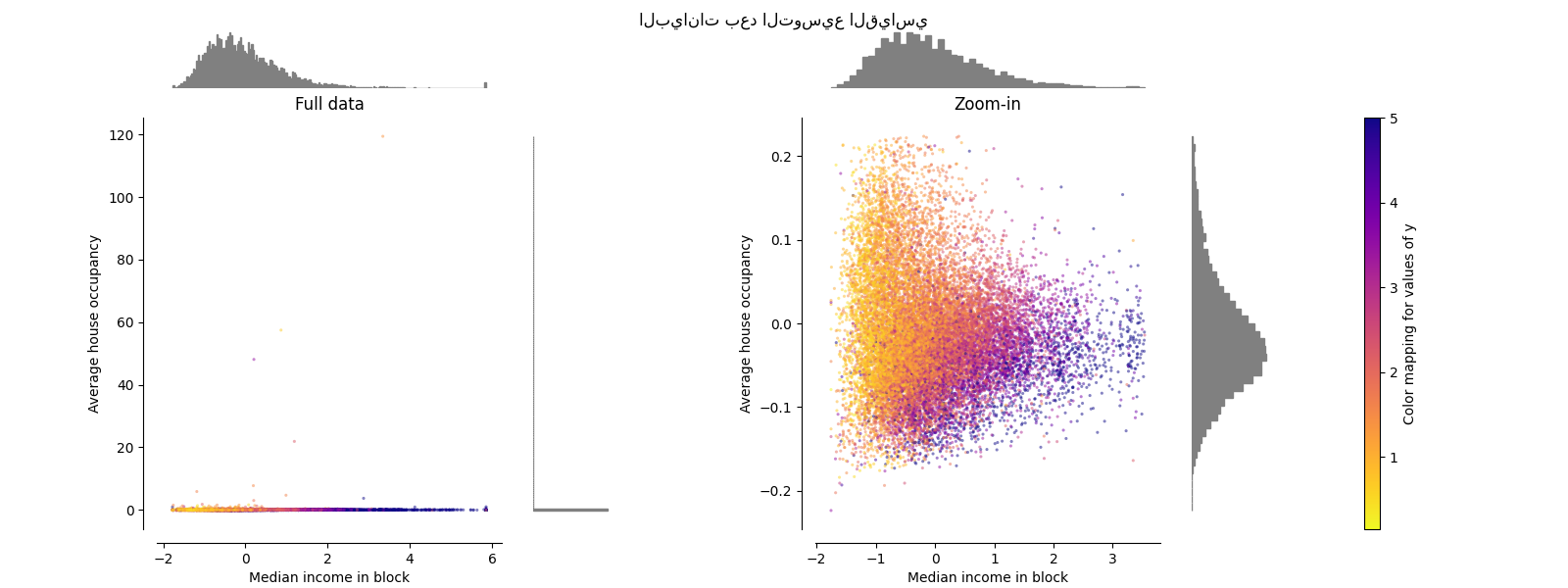
MinMaxScaler#
MinMaxScaler يعيد توسيع مجموعة البيانات بحيث
جميع قيم الميزات في
النطاق [0, 1] كما هو موضح في اللوحة اليمنى أدناه. ومع ذلك, يضغط هذا التوسيع
جميع القيم الداخلية إلى النطاق الضيق [0, 0.005] لشغل المنزل المحول.
كل من StandardScaler و
MinMaxScaler حساسة للغاية لوجود
القيم الشاذة.
make_plot(2)
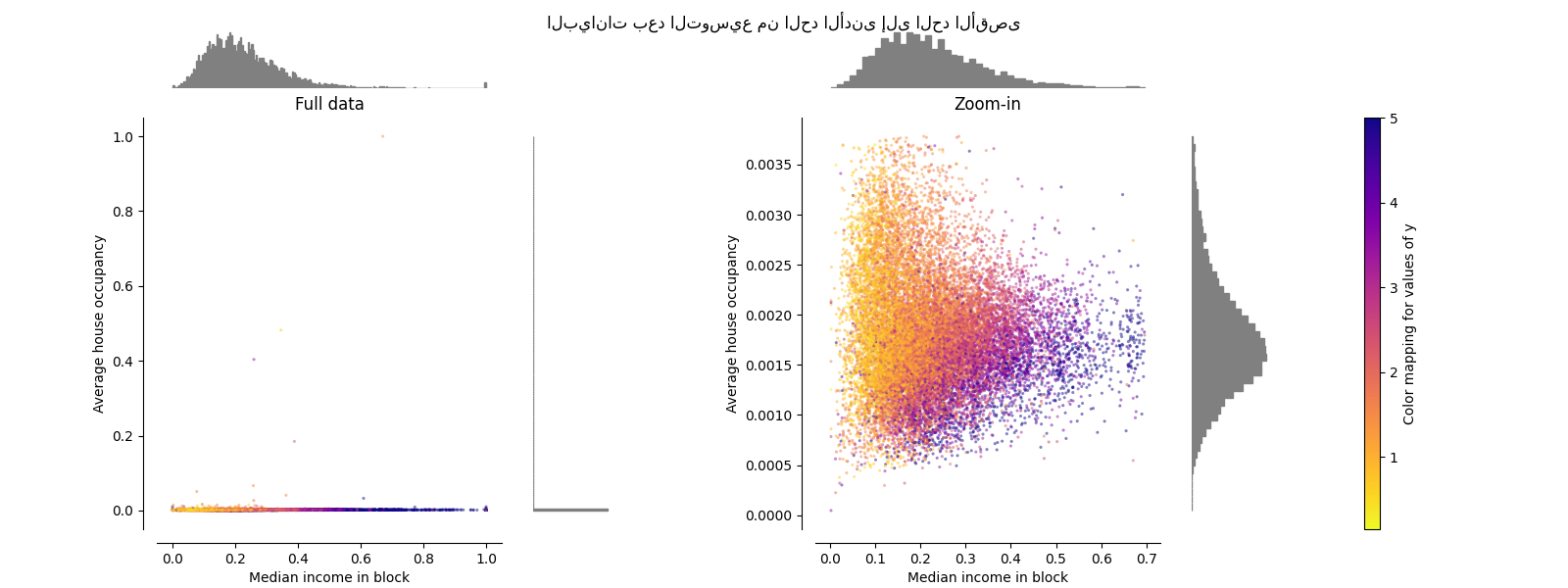
MaxAbsScaler#
MaxAbsScaler مشابه
MinMaxScaler باستثناء أن
القيم يتم رسمها عبر نطاقات متعددة اعتمادًا على ما إذا كانت القيم السلبية
أو الإيجابية موجودة. إذا كانت القيم الإيجابية فقط موجودة, يكون
النطاق [0, 1]. إذا كانت القيم السلبية فقط موجودة, يكون النطاق [-1, 0].
إذا كانت القيم السلبية والإيجابية موجودة, يكون النطاق [-1, 1].
على البيانات الإيجابية فقط, كل من MinMaxScaler
و MaxAbsScaler تتصرف بشكل مشابه.
MaxAbsScaler لذلك يعاني أيضًا من
وجود القيم الشاذة الكبيرة.
make_plot(3)
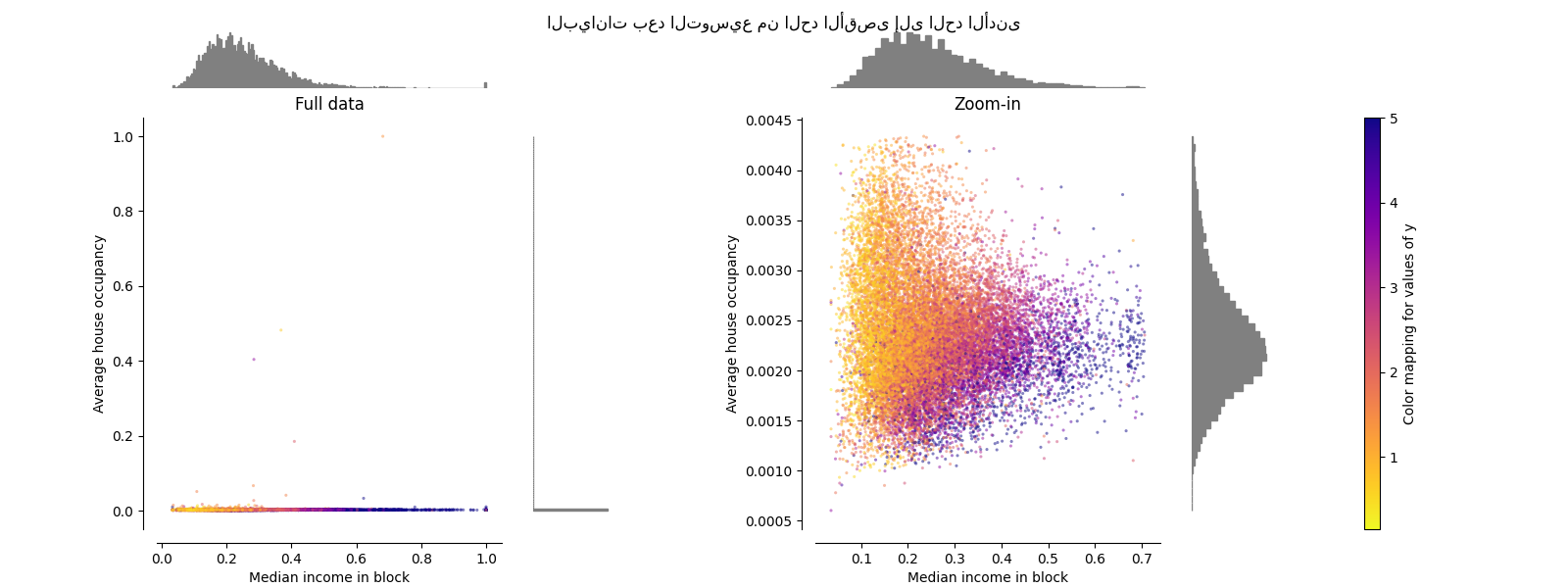
RobustScaler#
على عكس المقاييس السابقة, فإن إحصائيات التوسيط والتوسيع
RobustScaler
تعتمد على المئينات وبالتالي لا تتأثر بعدد صغير
من القيم الشاذة الهامشية الكبيرة جدًا. وبالتالي, فإن النطاق الناتج
لقيم الميزات المحولة أكبر من المقاييس السابقة, والأهم من ذلك,
تكون متشابهة تقريبًا: بالنسبة لكلتا الميزتين تقع معظم
القيم المحولة في نطاق [-2, 3] كما هو موضح في الرسم المكبر.
لاحظ أن القيم الشاذة نفسها لا تزال موجودة في البيانات المحولة.
إذا كان قص القيم الشاذة مرغوبًا فيه بشكل منفصل, فمن الضروري إجراء تحول غير خطي
(انظر أدناه).
make_plot(4)
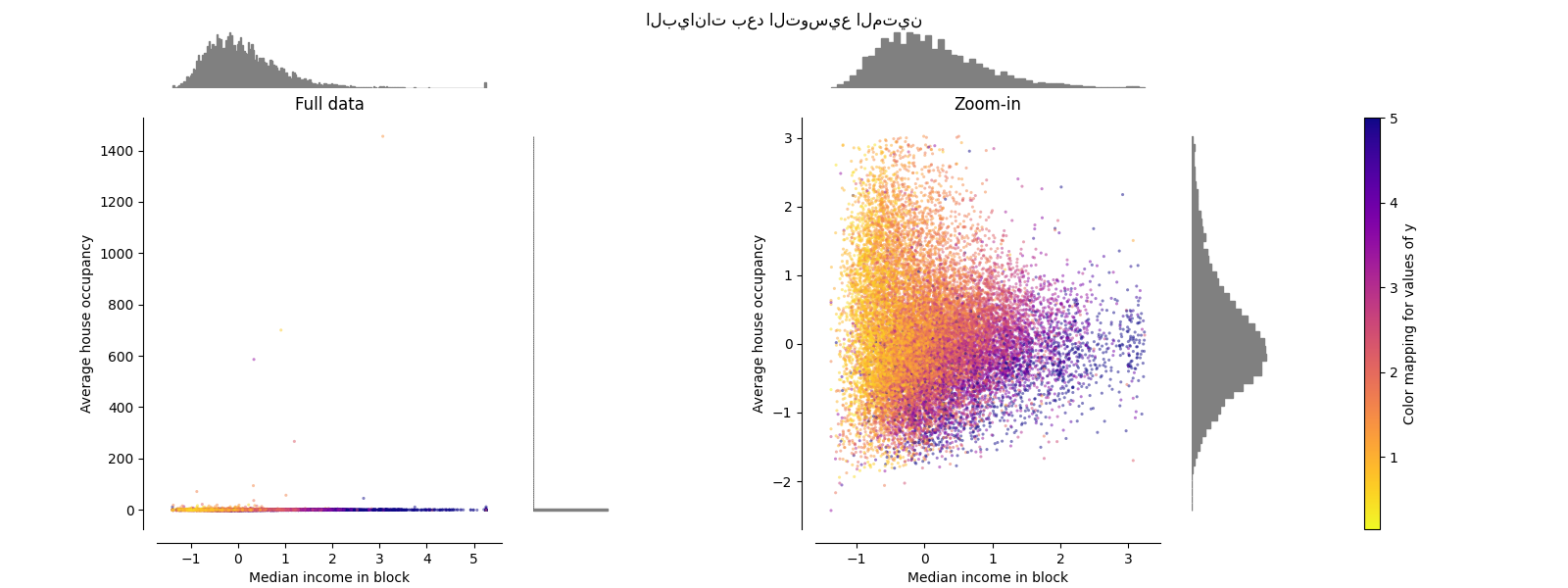
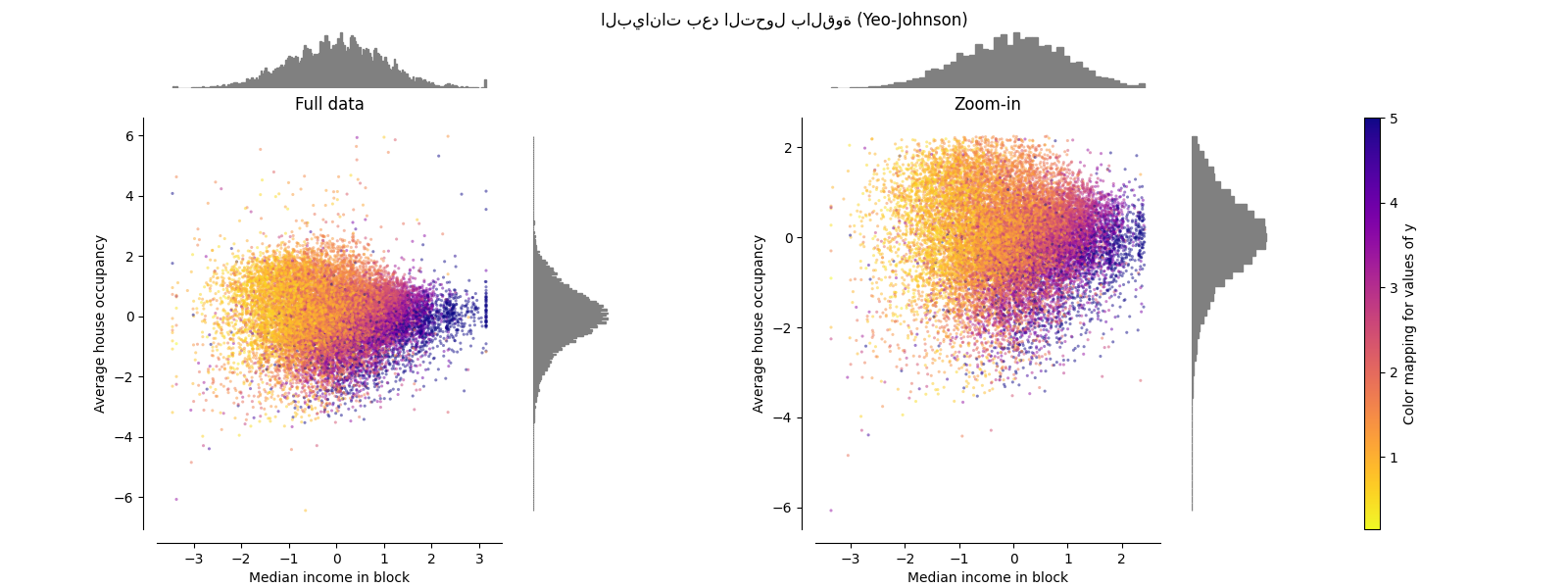
PowerTransformer#
يطبق PowerTransformer تحويلًا قويًا
على كل ميزة لجعل البيانات أشبه بالتوزيع الغاوسي من أجل
استقرار التباين وتقليل الانحراف. حاليًا، يتم دعم تحويلات Yeo-Johnson
و Box-Cox ويتم تحديد عامل القياس الأمثل عن طريق تقدير
الاحتمالية القصوى في كلتا الطريقتين. افتراضيًا، يطبق
PowerTransformer تطبيعًا صفريًا
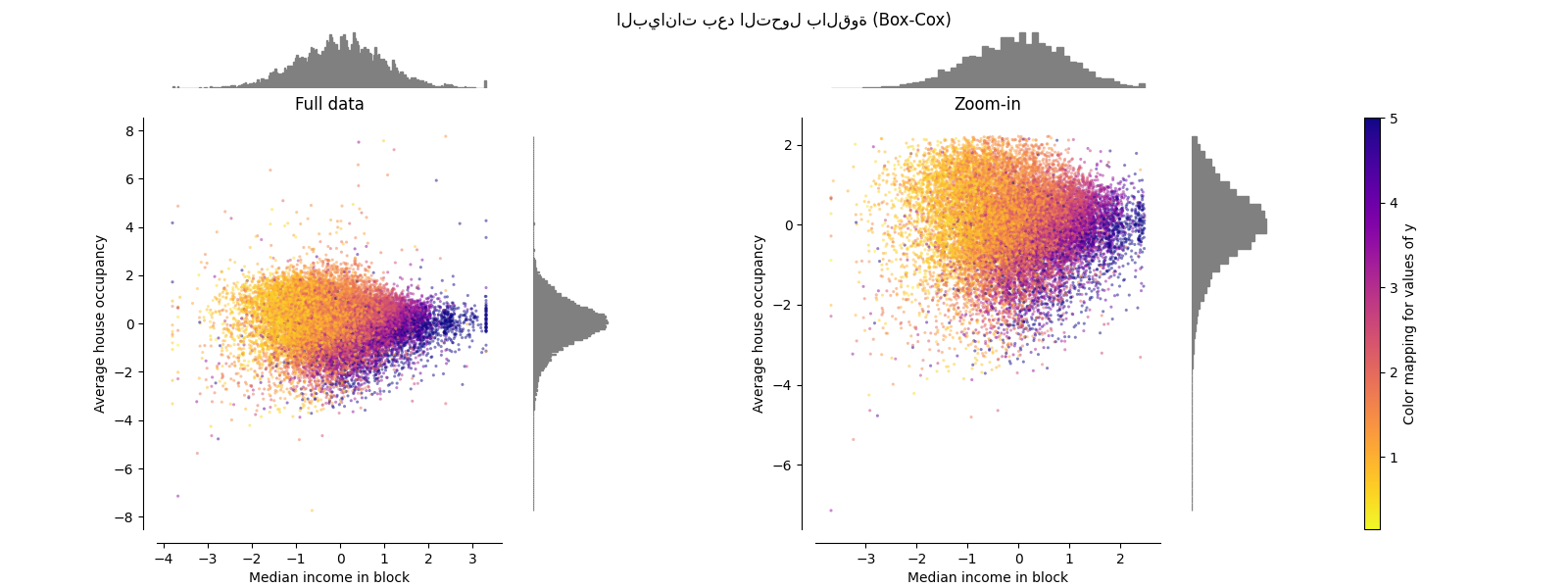
ومتوسطًا لوحدة التباين. لاحظ أنه لا يمكن تطبيق Box-Cox إلا على البيانات
الموجبة تمامًا. يحدث أن يكون الدخل ومتوسط إشغال المنزل موجبين
تمامًا، ولكن إذا كانت القيم السالبة موجودة، فإن تحويل Yeo-Johnson هو
المفضل.
make_plot(5)
make_plot(6)
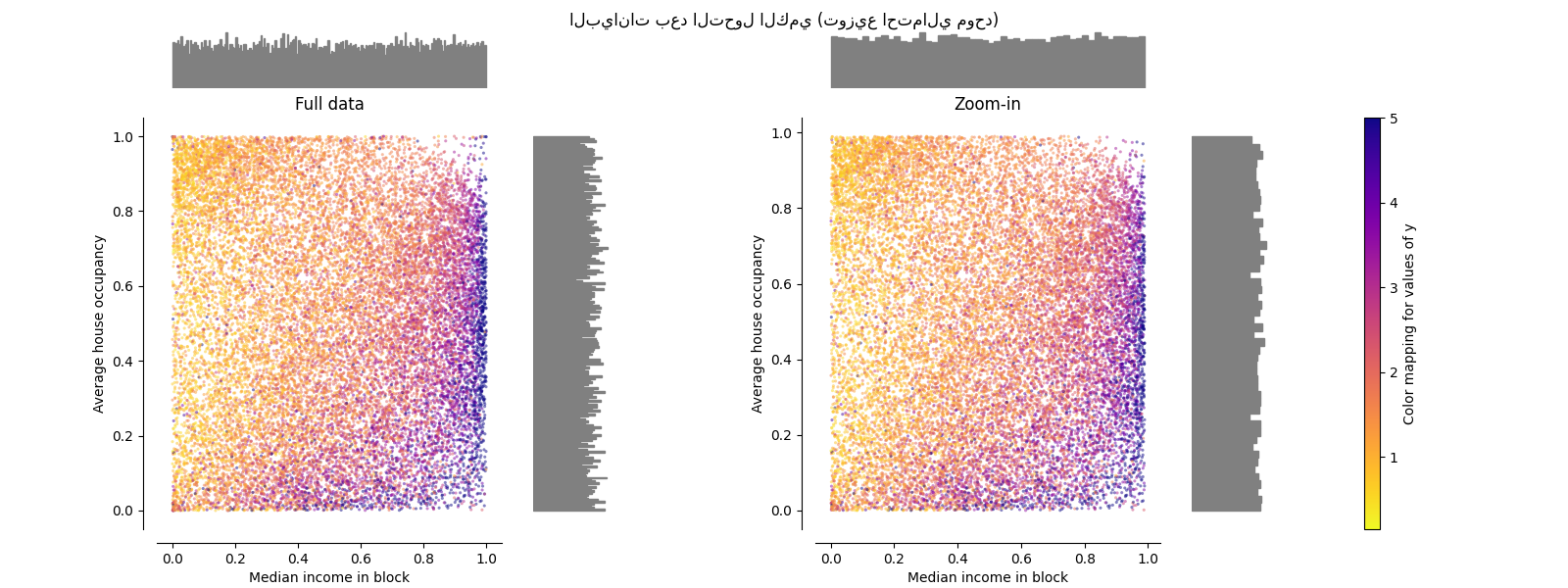
QuantileTransformer (مخرجات موحدة)#
يطبق QuantileTransformer تحويلًا غير خطي
بحيث يتم تعيين دالة كثافة الاحتمال لكل ميزة إلى توزيع
موحد أو غاوسي. في هذه الحالة، سيتم تعيين جميع البيانات، بما في ذلك
القيم المتطرفة، إلى توزيع موحد مع النطاق [0، 1]، مما يجعل
القيم المتطرفة لا يمكن تمييزها عن القيم الداخلية.
RobustScaler و
QuantileTransformer مقاومان للقيم
المتطرفة بمعنى أن إضافة أو إزالة القيم المتطرفة في مجموعة التدريب
سينتج عنهما نفس التحويل تقريبًا. ولكن على عكس
RobustScaler، فإن
QuantileTransformer سيقوم أيضًا
تلقائيًا بطي أي قيمة متطرفة عن طريق تعيينها على حدود النطاق المحددة
مسبقًا (0 و 1). يمكن أن يؤدي هذا إلى تشبع القطع الأثرية للقيم
المتطرفة.
make_plot(7)
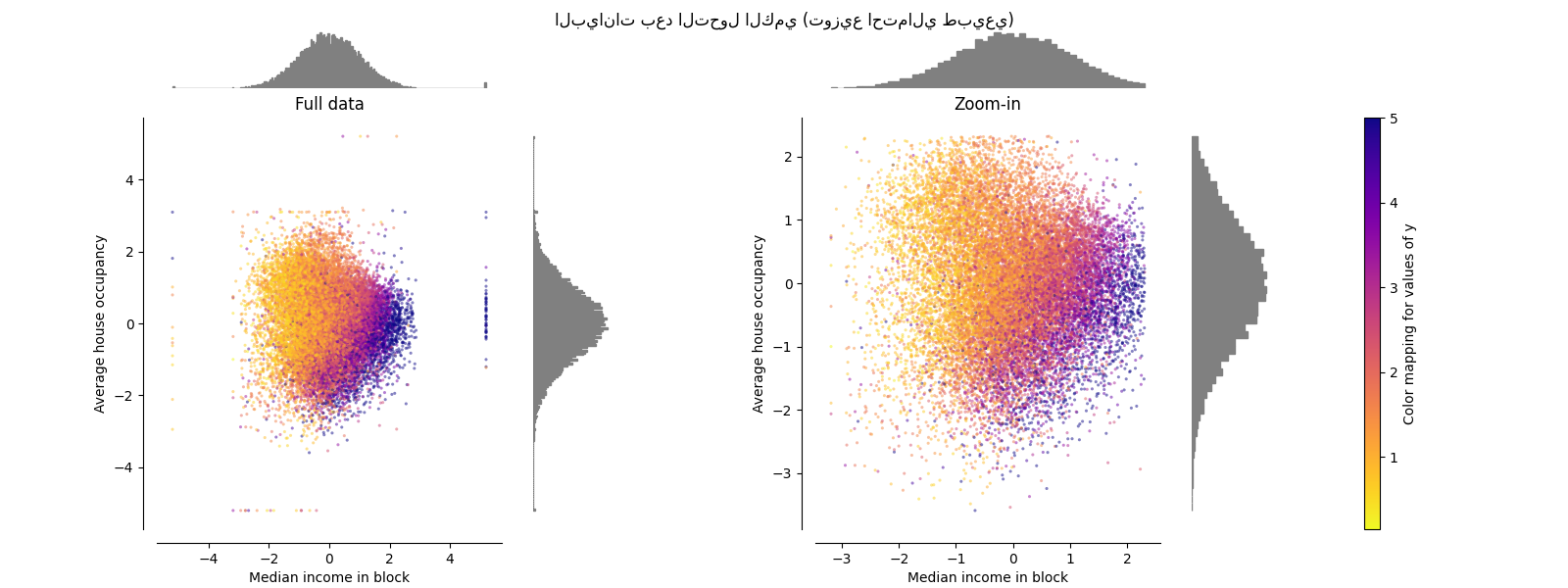
QuantileTransformer (مخرجات غاوسية)#
للتعيين إلى توزيع غاوسي، قم بتعيين المعلمة
output_distribution='normal'.
make_plot(8)
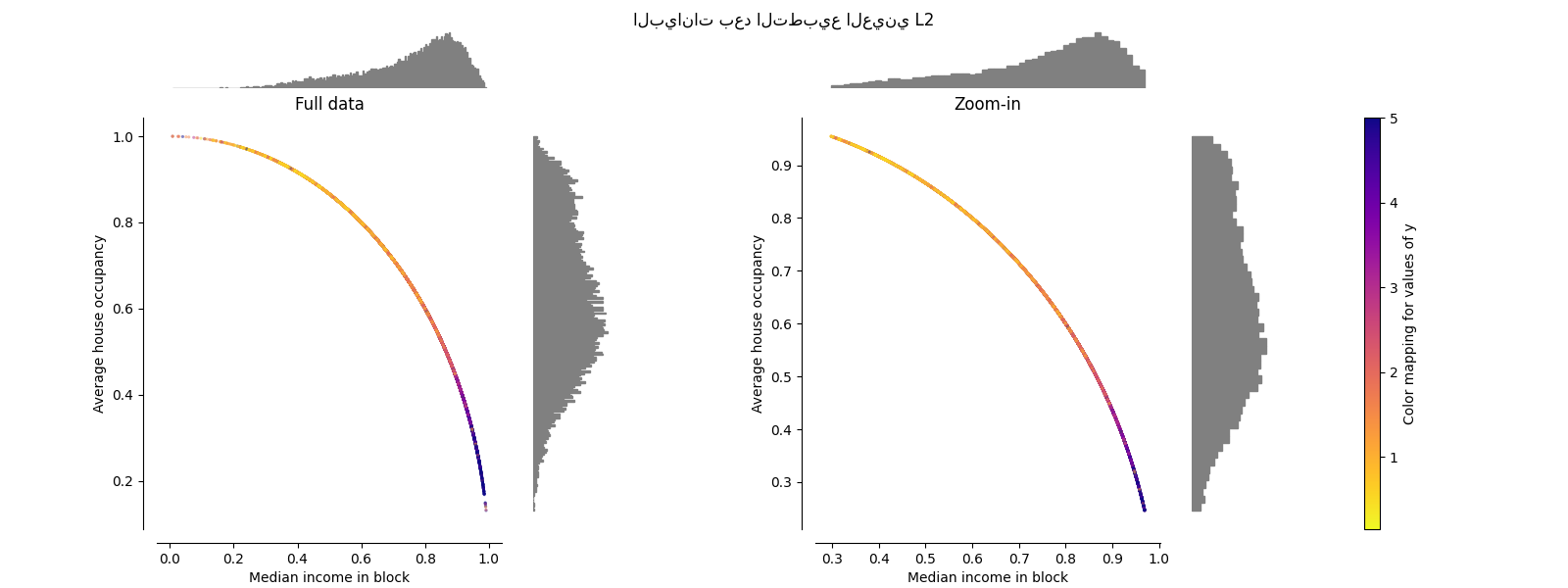
Normalizer#
يقوم Normalizer بإعادة قياس المتجه لكل
عينة ليكون له معيار وحدة، بشكل مستقل عن توزيع العينات. يمكن رؤيته
في كلا الشكلين أدناه حيث يتم تعيين جميع العينات على دائرة الوحدة. في
مثالنا، تحتوي الميزتان المحددتان على قيم موجبة فقط؛ لذلك تقع البيانات
المحولة فقط في الربع الموجب. لن يكون هذا هو الحال إذا كانت بعض
الميزات الأصلية تحتوي على مزيج من القيم الموجبة والسالبة.
make_plot(9)
plt.show()
Total running time of the script: (0 minutes 10.370 seconds)
Related examples
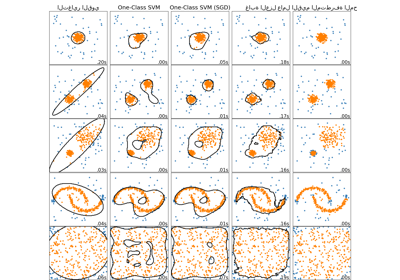
مقارنة خوارزميات الكشف عن الشذوذ لكشف القيم المتطرفة في مجموعات بيانات تجريبية
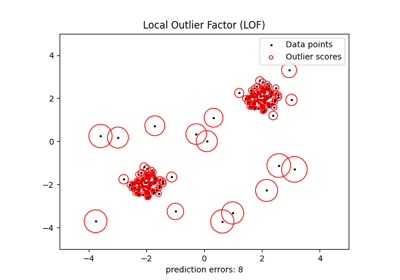
الكشف عن القيم الشاذة باستخدام عامل الانحراف المحلي (LOF)