أهمية معايرة الميزات

تعد معايرة الميزات من خلال التوحيد القياسي، والتي تسمى أيضًا التوحيد القياسي Z-score، خطوة معالجة مسبقة مهمة للعديد من خوارزميات التعلم الآلي. تتضمن إعادة معايرة كل ميزة بحيث يكون لها انحراف معياري يساوي 1 ومتوسط يساوي 0.

حتى إذا كانت النماذج القائمة على الشجرة (تقريبًا) غير متأثرة بالمعايرة، فإن العديد من الخوارزميات الأخرى تتطلب معايرة الميزات، غالبًا لأسباب مختلفة: لتسهيل التقارب (مثل الانحدار اللوجستي غير المعاقب)، لإنشاء نموذج مختلف تمامًا مقارنةً بالملاءمة مع البيانات غير المعايرة (مثل نماذج KNeighbors). يتم توضيح الأخير في الجزء الأول من المثال الحالي.

في الجزء الثاني من المثال، نوضح كيف يتأثر التحليل الرئيسي للمكونات (PCA) بتطبيع الميزات. لتوضيح ذلك، نقارن المكونات الرئيسية التي تم العثور عليها باستخدام PCA على البيانات غير المعايرة بتلك التي تم الحصول عليها عند استخدام StandardScaler لمعايرة البيانات أولاً.

في الجزء الأخير من المثال، نوضح تأثير التطبيع على دقة النموذج الذي تم تدريبه على البيانات المخفضة باستخدام PCA.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

تحميل وإعداد البيانات

مجموعة البيانات المستخدمة هي Wine recognition dataset المتاحة في UCI. تحتوي هذه المجموعة من البيانات على ميزات مستمرة ذات مقاييس متغايرة بسبب الخصائص المختلفة التي تقيسها (مثل محتوى الكحول وحمض الماليك).

from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

X, y = load_wine(return_X_y=True, as_frame=True)
scaler = StandardScaler().set_output(transform="pandas")

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.30, random_state=42
)
scaled_X_train = scaler.fit_transform(X_train)

تأثير إعادة المعايرة على نماذج k-neighbors

من أجل تصور حدود القرار لتصنيف KNeighborsClassifier، في هذا القسم، نختار مجموعة فرعية من ميزتين لهما قيم ذات ترتيبات مختلفة من حيث الحجم.

ضع في اعتبارك أن استخدام مجموعة فرعية من الميزات لتدريب النموذج قد يؤدي إلى ترك ميزات ذات تأثير تنبؤي عالٍ، مما يؤدي إلى حدود قرار أسوأ بكثير مقارنةً بالنموذج الذي تم تدريبه على المجموعة الكاملة من الميزات.

import matplotlib.pyplot as plt

from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.neighbors import KNeighborsClassifier

X_plot = X[["proline", "hue"]]
X_plot_scaled = scaler.fit_transform(X_plot)
clf = KNeighborsClassifier(n_neighbors=20)


def fit_and_plot_model(X_plot, y, clf, ax):
    clf.fit(X_plot, y)
    disp = DecisionBoundaryDisplay.from_estimator(
        clf,
        X_plot,
        response_method="predict",
        alpha=0.5,
        ax=ax,
    )
    disp.ax_.scatter(X_plot["proline"], X_plot["hue"], c=y, s=20, edgecolor="k")
    disp.ax_.set_xlim((X_plot["proline"].min(), X_plot["proline"].max()))
    disp.ax_.set_ylim((X_plot["hue"].min(), X_plot["hue"].max()))
    return disp.ax_


fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 6))

fit_and_plot_model(X_plot, y, clf, ax1)
ax1.set_title("KNN بدون معايرة")

fit_and_plot_model(X_plot_scaled, y, clf, ax2)
ax2.set_xlabel("proline المعاير")
ax2.set_ylabel("hue المعاير")
_ = ax2.set_title("KNN مع المعايرة")

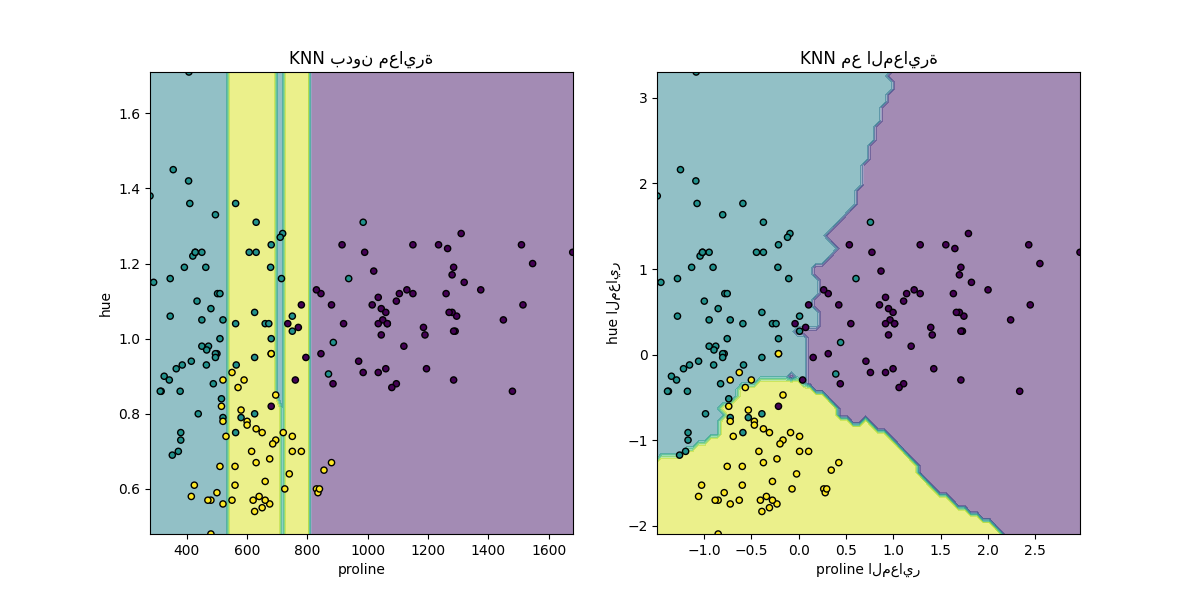
هنا، توضح حدود القرار أن ملاءمة البيانات المعايرة أو غير المعايرة تؤدي إلى نماذج مختلفة تمامًا. والسبب هو أن المتغير "proline" له قيم تتراوح بين 0 و 1,000؛ في حين أن المتغير "hue" يتراوح بين 1 و 10. بسبب هذا، تتأثر المسافات بين العينات بشكل أساسي بالاختلافات في قيم "proline"، في حين يتم تجاهل قيم "hue" بشكل نسبي. إذا استخدم المرء StandardScaler لتطبيع هذه القاعدة البيانات، كلتا القيمتين المعايرتين تقع تقريبًا بين -3 و 3، وتتأثر بنية الجيران بشكل متساوٍ تقريبًا من خلال كلا المتغيرين.

تأثير إعادة المعايرة على خفض الأبعاد باستخدام PCA

يتكون خفض الأبعاد باستخدام PCA من العثور على الميزات التي تزيد من التباين. إذا كانت إحدى الميزات تختلف أكثر من غيرها فقط بسبب مقاييسها، PCA سيحدد أن هذه الميزة تهيمن على اتجاه المكونات الرئيسية.

يمكننا فحص المكونات الرئيسية الأولى باستخدام جميع الميزات الأصلية:

import pandas as pd

from sklearn.decomposition import PCA

pca = PCA(n_components=2).fit(X_train)
scaled_pca = PCA(n_components=2).fit(scaled_X_train)
X_train_transformed = pca.transform(X_train)
X_train_std_transformed = scaled_pca.transform(scaled_X_train)

first_pca_component = pd.DataFrame(
    pca.components_[0], index=X.columns, columns=["بدون معايرة"]
)
first_pca_component["مع المعايرة"] = scaled_pca.components_[0]
first_pca_component.plot.bar(
    title="أوزان المكون الرئيسي الأول", figsize=(6, 8)
)

_ = plt.tight_layout()

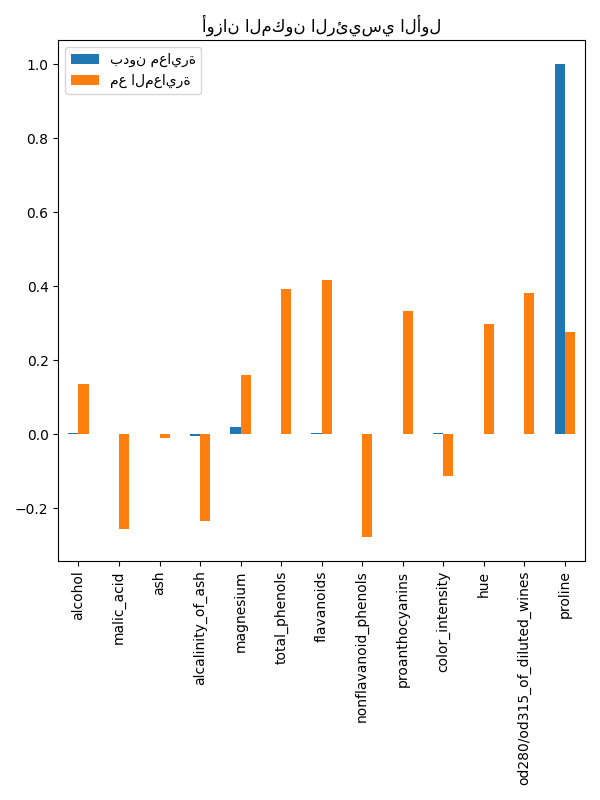
بالفعل نجد أن ميزة "proline" تهيمن على اتجاه المكون الرئيسي الأول بدون معايرة، حيث تكون أعلى بحوالي مرتبتين من الحجم من الميزات الأخرى. وهذا يتناقض عند ملاحظة المكون الرئيسي الأول لنسخة البيانات المعايرة، حيث تكون مراتب الحجم متشابهة تقريبًا عبر جميع الميزات.

يمكننا تصور توزيع المكونات الرئيسية في كلتا الحالتين:

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))

target_classes = range(0, 3)
colors = ("blue", "red", "green")
markers = ("^", "s", "o")

for target_class, color, marker in zip(target_classes, colors, markers):
    ax1.scatter(
        x=X_train_transformed[y_train == target_class, 0],
        y=X_train_transformed[y_train == target_class, 1],
        color=color,
        label=f"class {target_class}",
        alpha=0.5,
        marker=marker,
    )

    ax2.scatter(
        x=X_train_std_transformed[y_train == target_class, 0],
        y=X_train_std_transformed[y_train == target_class, 1],
        color=color,
        label=f"class {target_class}",
        alpha=0.5,
        marker=marker,
    )

ax1.set_title("مجموعة البيانات التدريبية غير المعايرة بعد PCA")
ax2.set_title("مجموعة البيانات التدريبية المعايرة بعد PCA")

for ax in (ax1, ax2):
    ax.set_xlabel("المكون الرئيسي الأول")
    ax.set_ylabel("المكون الرئيسي الثاني")
    ax.legend(loc="upper right")
    ax.grid()

_ = plt.tight_layout()

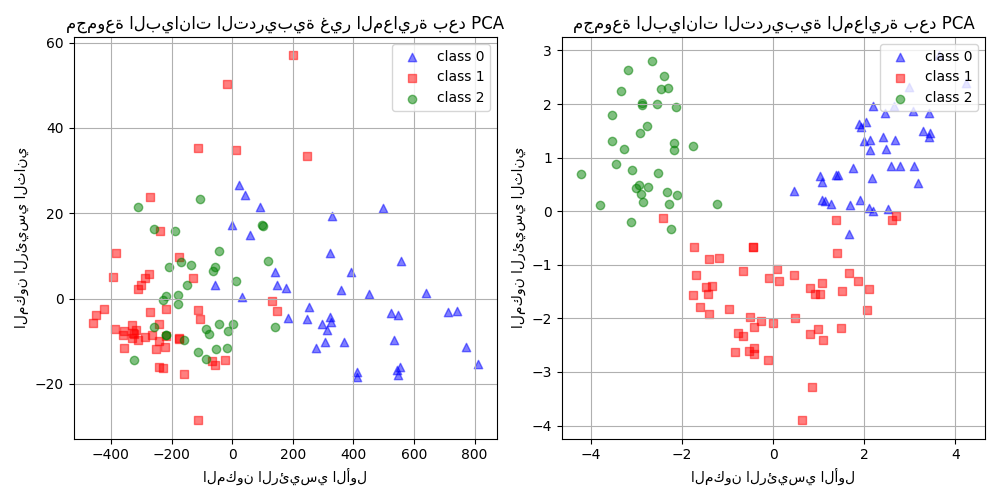
من الرسم البياني أعلاه، نلاحظ أن معايرة الميزات قبل خفض الأبعاد يؤدي إلى مكونات بنفس ترتيب الحجم. في هذه الحالة، يحسن أيضًا قابلية فصل الفئات. بالفعل، في القسم التالي نؤكد أن قابلية الفصل الأفضل لها تأثير جيد على الأداء العام للنموذج.

تأثير إعادة المعايرة على أداء النموذج

أولاً، نوضح كيف يعتمد التنظيم الأمثل لتصنيف LogisticRegressionCV على معايرة البيانات أو عدم معايرتها:

import numpy as np

from sklearn.linear_model import LogisticRegressionCV
from sklearn.pipeline import make_pipeline

Cs = np.logspace(-5, 5, 20)

unscaled_clf = make_pipeline(pca, LogisticRegressionCV(Cs=Cs))
unscaled_clf.fit(X_train, y_train)

scaled_clf = make_pipeline(scaler, pca, LogisticRegressionCV(Cs=Cs))
scaled_clf.fit(X_train, y_train)

print(f"القيمة المثلى C للـ PCA غير المعاير: {unscaled_clf[-1].C_[0]:.4f}\n")
print(f"القيمة المثلى C للبيانات المعايرة مع PCA: {scaled_clf[-1].C_[0]:.2f}")

القيمة المثلى C للـ PCA غير المعاير: 0.0004

القيمة المثلى C للبيانات المعايرة مع PCA: 20.69

الحاجة إلى التنظيم أعلى (قيم أقل لـ C) للبيانات التي لم يتم معايرتها قبل تطبيق PCA. نقوم الآن بتقييم تأثير المعايرة على دقة ومتوسط خسارة اللوغاريتم للنموذجين الأمثلين:

from sklearn.metrics import accuracy_score, log_loss

y_pred = unscaled_clf.predict(X_test)
y_pred_scaled = scaled_clf.predict(X_test)
y_proba = unscaled_clf.predict_proba(X_test)
y_proba_scaled = scaled_clf.predict_proba(X_test)

print("دقة الاختبار لـ PCA غير المعاير")
print(f"{accuracy_score(y_test, y_pred):.2%}\n")
print("دقة الاختبار للبيانات المعايرة مع PCA")
print(f"{accuracy_score(y_test, y_pred_scaled):.2%}\n")
print("خسارة اللوغاريتم لـ PCA غير المعاير")
print(f"{log_loss(y_test, y_proba):.3}\n")
print("خسارة اللوغاريتم للبيانات المعايرة مع PCA")
print(f"{log_loss(y_test, y_proba_scaled):.3}")

دقة الاختبار لـ PCA غير المعاير
35.19%

دقة الاختبار للبيانات المعايرة مع PCA
96.30%

خسارة اللوغاريتم لـ PCA غير المعاير
0.957

خسارة اللوغاريتم للبيانات المعايرة مع PCA
0.0825

يتم ملاحظة اختلاف واضح في دقة التنبؤ عند معايرة البيانات قبل PCA، حيث تتفوق بشكل كبير على النسخة غير المعايرة. ويتوافق هذا مع الحدس الذي تم الحصول عليه من الرسم البياني في القسم السابق، حيث تصبح المكونات قابلة للفصل خطيًا عند المعايرة قبل استخدام PCA.

لاحظ أنه في هذه الحالة، تؤدي النماذج ذات الميزات المعايرة أداءً أفضل من النماذج ذات الميزات غير المعايرة لأن جميع المتغيرات من المتوقع أن تكون تنبؤية ونحن نتجنب بعضها أن يتم تجاهلها نسبيًا.

إذا كانت المتغيرات في المقاييس المنخفضة غير تنبؤية، فقد يواجه المرء انخفاضًا في الأداء بعد معايرة الميزات: ستساهم الميزات الضجيجية أكثر في التنبؤ بعد المعايرة وبالتالي ستزيد المعايرة من الإفراط في الملاءمة.

وأخيرًا وليس آخرًا، نلاحظ أننا نحقق خسارة لوغاريتم أقل من خلال خطوة المعايرة.

Related examples

مقارنة معايرة المصنفات

مقارنة معايرة المصنفات

منحنيات معايرة الاحتمالية

منحنيات معايرة الاحتمالية

معايرة الاحتمالات لتصنيف ثلاثي الفئات

معايرة الاحتمالات لتصنيف ثلاثي الفئات

# مقارنة المنحنيات الخطية للانحدار البايزي

# مقارنة المنحنيات الخطية للانحدار البايزي