تحويل البيانات إلى التوزيع الطبيعي

هذا المثال يوضح استخدام تحويلات Box-Cox وYeo-Johnson من خلال PowerTransformer لتحويل البيانات من توزيعات مختلفة إلى التوزيع الطبيعي.

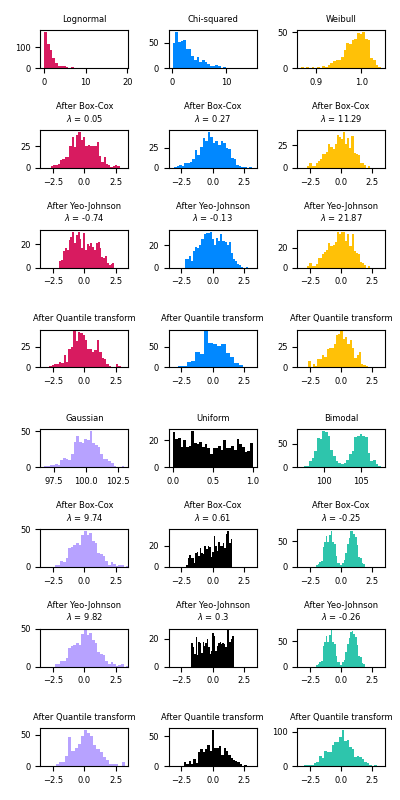
التحويل بالقوة مفيد كتحويل في مشاكل النمذجة حيث يتم الرغبة في التجانس والتوزيع الطبيعي. فيما يلي أمثلة على تطبيق Box-Cox و Yeo-Johnwon على ستة توزيعات احتمالية مختلفة: اللوغاريتمي الطبيعي، مربع كاي، ويبل، الجاوسي، الموحد، ثنائي النمط.

ملاحظة أن التحولات تنجح في تحويل البيانات إلى توزيع طبيعي عند تطبيقها على مجموعات بيانات معينة، ولكنها غير فعالة مع مجموعات أخرى. هذا يسلط الضوء على أهمية تصور البيانات قبل وبعد التحويل.

لاحظ أيضًا أنه على الرغم من أن Box-Cox يبدو أنه يؤدي بشكل أفضل من Yeo-Johnson للتوزيعات اللوغاريتمية الطبيعية ومربعة كاي، إلا أنه يجب مراعاة أن Box-Cox لا يدعم المدخلات ذات القيم السالبة.

لمقارنة، نضيف أيضًا الناتج من QuantileTransformer. يمكنه فرض أي توزيع تعسفي إلى التوزيع الجاوسي، بشرط أن يكون هناك ما يكفي من عينات التدريب (الآلاف). لأنه طريقة غير معلمية، من الصعب تفسيرها أكثر من الطرق المعلمية (Box-Cox وYeo-Johnson).

على مجموعات البيانات "الصغيرة" (أقل من بضع مئات من النقاط)، محول الكوانتيل عرضة لخطر الإفراط في التحديد. يوصى باستخدام التحويل بالقوة.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PowerTransformer, QuantileTransformer

N_SAMPLES = 1000
FONT_SIZE = 6
BINS = 30


rng = np.random.RandomState(304)
bc = PowerTransformer(method="box-cox")
yj = PowerTransformer(method="yeo-johnson")
# n_quantiles is set to the training set size rather than the default value
# to avoid a warning being raised by this example
qt = QuantileTransformer(
    n_quantiles=500, output_distribution="normal", random_state=rng
)
size = (N_SAMPLES, 1)


# التوزيع اللوغاريتمي الطبيعي
X_lognormal = rng.lognormal(size=size)

# توزيع مربع كاي
df = 3
X_chisq = rng.chisquare(df=df, size=size)

# توزيع ويبل
a = 50
X_weibull = rng.weibull(a=a, size=size)

# التوزيع الجاوسي
loc = 100
X_gaussian = rng.normal(loc=loc, size=size)

# التوزيع الموحد
X_uniform = rng.uniform(low=0, high=1, size=size)

# التوزيع ثنائي النمط
loc_a, loc_b = 100, 105
X_a, X_b = rng.normal(loc=loc_a, size=size), rng.normal(loc=loc_b, size=size)
X_bimodal = np.concatenate([X_a, X_b], axis=0)


# إنشاء الرسوم البيانية
distributions = [
    ("Lognormal", X_lognormal),
    ("Chi-squared", X_chisq),
    ("Weibull", X_weibull),
    ("Gaussian", X_gaussian),
    ("Uniform", X_uniform),
    ("Bimodal", X_bimodal),
]

colors = ["#D81B60", "#0188FF", "#FFC107", "#B7A2FF", "#000000", "#2EC5AC"]

fig, axes = plt.subplots(nrows=8, ncols=3, figsize=plt.figaspect(2))
axes = axes.flatten()
axes_idxs = [
    (0, 3, 6, 9),
    (1, 4, 7, 10),
    (2, 5, 8, 11),
    (12, 15, 18, 21),
    (13, 16, 19, 22),
    (14, 17, 20, 23),
]
axes_list = [(axes[i], axes[j], axes[k], axes[l]) for (i, j, k, l) in axes_idxs]


for distribution, color, axes in zip(distributions, colors, axes_list):
    name, X = distribution
    X_train, X_test = train_test_split(X, test_size=0.5)

    # إجراء تحويلات القوة وتحويل الكوانتيل
    X_trans_bc = bc.fit(X_train).transform(X_test)
    lmbda_bc = round(bc.lambdas_[0], 2)
    X_trans_yj = yj.fit(X_train).transform(X_test)
    lmbda_yj = round(yj.lambdas_[0], 2)
    X_trans_qt = qt.fit(X_train).transform(X_test)

    ax_original, ax_bc, ax_yj, ax_qt = axes

    ax_original.hist(X_train, color=color, bins=BINS)
    ax_original.set_title(name, fontsize=FONT_SIZE)
    ax_original.tick_params(axis="both", which="major", labelsize=FONT_SIZE)

    for ax, X_trans, meth_name, lmbda in zip(
        (ax_bc, ax_yj, ax_qt),
        (X_trans_bc, X_trans_yj, X_trans_qt),
        ("Box-Cox", "Yeo-Johnson", "Quantile transform"),
        (lmbda_bc, lmbda_yj, None),
    ):
        ax.hist(X_trans, color=color, bins=BINS)
        title = "After {}".format(meth_name)
        if lmbda is not None:
            title += "\n$\\lambda$ = {}".format(lmbda)
        ax.set_title(title, fontsize=FONT_SIZE)
        ax.tick_params(axis="both", which="major", labelsize=FONT_SIZE)
        ax.set_xlim([-3.5, 3.5])


plt.tight_layout()
plt.show()

Related examples

مقارنة تأثير المقياس المختلف على البيانات مع القيم الشاذة

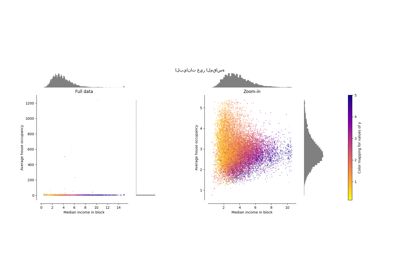
مقارنة تأثير المقياس المختلف على البيانات مع القيم الشاذة

sphx_glr_auto_examples_linear_model_plot_bayesian_ridge_curvefit.py

# ========================================================

إيقاف التدريب المبكر في Gradient Boosting

إيقاف التدريب المبكر في Gradient Boosting

ضبط معامل الانتظام لخوارزمية SVC

ضبط معامل الانتظام لخوارزمية SVC