ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
تحليل المكونات الرئيسية (PCA) على مجموعة بيانات Iris#
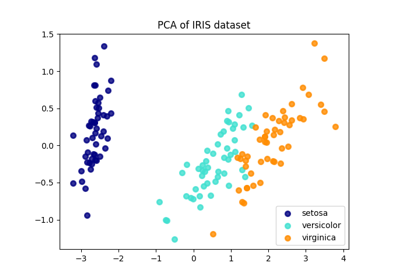
هذا المثال يوضح تقنية تحليل معروفة باسم تحليل المكونات الرئيسية (PCA) على مجموعة بيانات Iris.
تتكون هذه المجموعة من 4 خصائص: طول الكأس، وعرض الكأس، وطول البتلة، وعرض البتلة. نستخدم PCA لإسقاط هذا الفضاء المكون من 4 خصائص إلى فضاء ثلاثي الأبعاد.
# المؤلفون: مطوري scikit-learn
# معرف رخصة SPDX: BSD-3-Clause
تحميل مجموعة بيانات Iris#
مجموعة بيانات Iris متوفرة مباشرة كجزء من scikit-learn. يمكن تحميلها
باستخدام الدالة load_iris. مع المعاملات الافتراضية،
يتم إرجاع كائن Bunch، والذي يحتوي على البيانات،
والقيم المستهدفة، وأسماء الخصائص، وأسماء الأهداف.
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])
رسم بياني لأزواج الخصائص في مجموعة بيانات Iris#
دعنا نرسم أولاً أزواج الخصائص في مجموعة بيانات Iris.
import seaborn as sns
# إعادة تسمية الفئات باستخدام أسماء الأهداف في مجموعة بيانات Iris
iris.frame["target"] = iris.target_names[iris.target]
_ = sns.pairplot(iris.frame, hue="target")
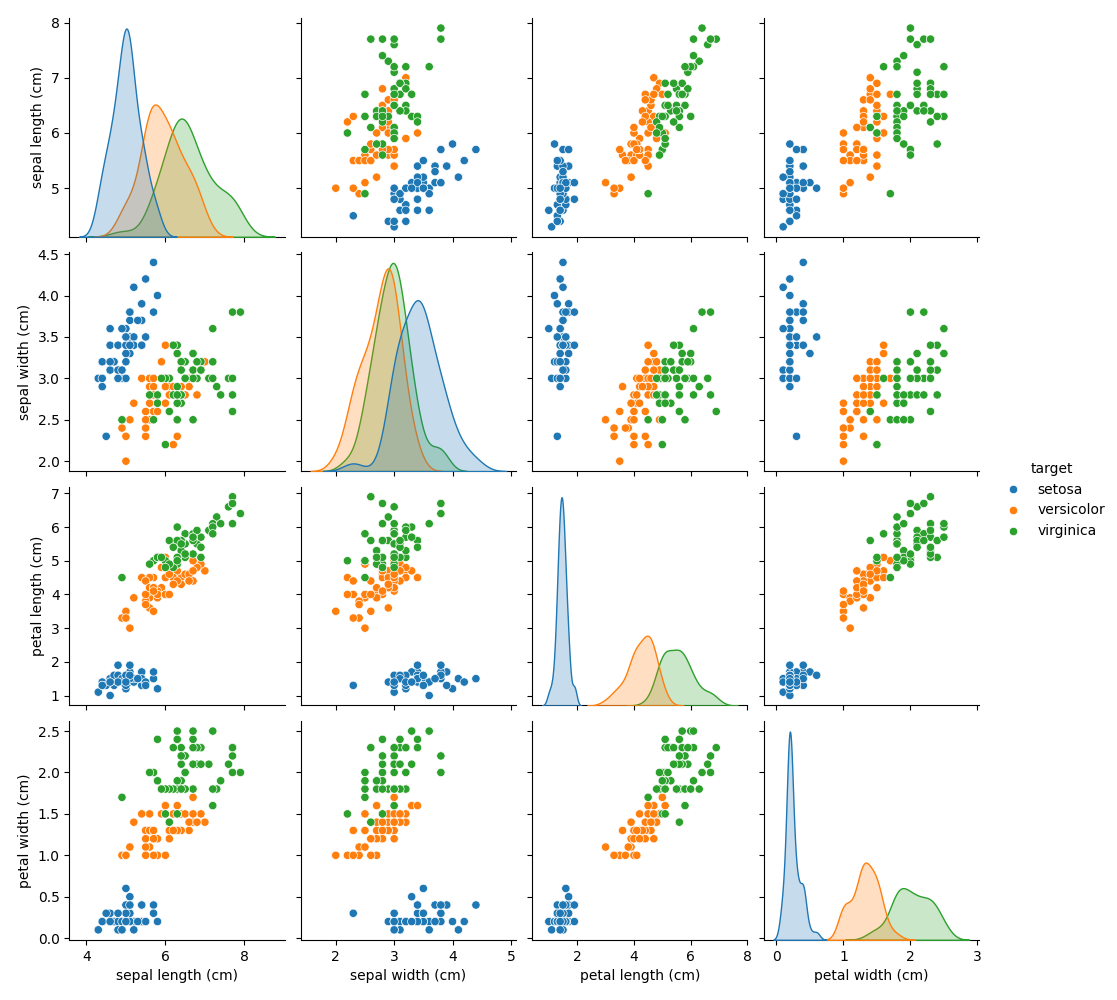
كل نقطة بيانات على كل رسم بياني متفرق تشير إلى واحدة من زهور Iris الـ 150 في مجموعة البيانات، مع الإشارة إلى لونها إلى نوعها (Setosa، وVersicolor، وVirginica).
يمكنك بالفعل ملاحظة نمط فيما يتعلق بنوع Setosa، والذي يمكن تحديده بسهولة بناءً على كأسها القصير والعريض. فقط بالنظر إلى هذين البعدين، طول وعرض الكأس، لا يزال هناك تداخل بين نوعي Versicolor وVirginica.
يُظهر القطر التوزيع لكل خاصية. نلاحظ أن عرض البتلة وطول البتلة هما أكثر الخصائص تمييزًا للأنواع الثلاثة.
رسم تمثيل PCA#
دعنا نطبق تحليل المكونات الرئيسية (PCA) على مجموعة بيانات Iris ثم نرسم زهور Iris عبر الأبعاد الثلاثة الأولى لـ PCA. سيسمح لنا ذلك بالتمييز بشكل أفضل بين الأنواع الثلاثة!
import matplotlib.pyplot as plt
# استيراد غير مستخدم ولكنه مطلوب للقيام بالرسوم البيانية ثلاثية الأبعاد باستخدام matplotlib < 3.2
import mpl_toolkits.mplot3d # noqa: F401
from sklearn.decomposition import PCA
fig = plt.figure(1, figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d", elev=-150, azim=110)
X_reduced = PCA(n_components=3).fit_transform(iris.data)
scatter = ax.scatter(
X_reduced[:, 0],
X_reduced[:, 1],
X_reduced[:, 2],
c=iris.target,
s=40,
)
ax.set(
title="First three PCA dimensions",
xlabel="1st Eigenvector",
ylabel="2nd Eigenvector",
zlabel="3rd Eigenvector",
)
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax.zaxis.set_ticklabels([])
# إضافة أسطورة
legend1 = ax.legend(
scatter.legend_elements()[0],
iris.target_names.tolist(),
loc="upper right",
title="Classes",
)
ax.add_artist(legend1)
plt.show()
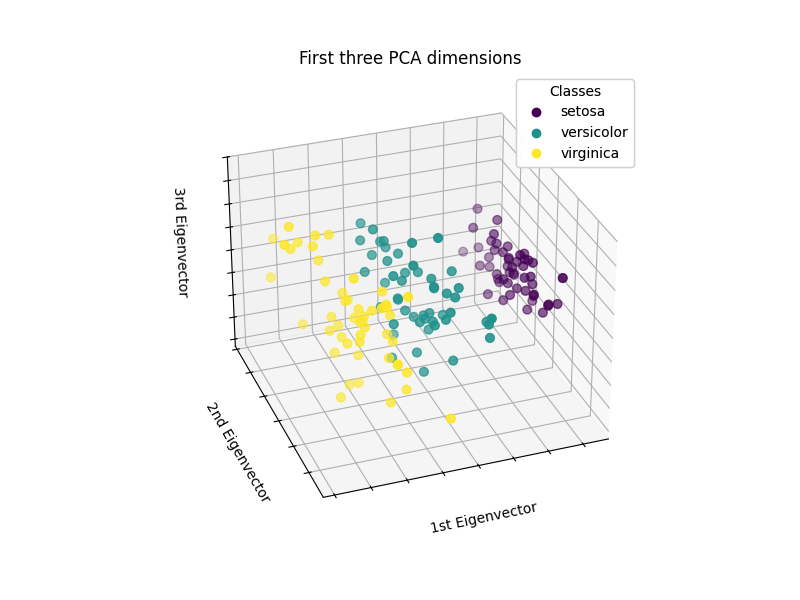
ستقوم PCA بإنشاء 3 خصائص جديدة تكون مزيجًا خطيًا من الخصائص الأصلية الـ 4. بالإضافة إلى ذلك، تُعظِّم هذه التحويلة التباين. مع هذا التحويل، نرى أنه يمكننا تحديد كل نوع باستخدام الخاصية الأولى فقط (أي، المتجه الذاتي الأول).
Total running time of the script: (0 minutes 3.495 seconds)
Related examples
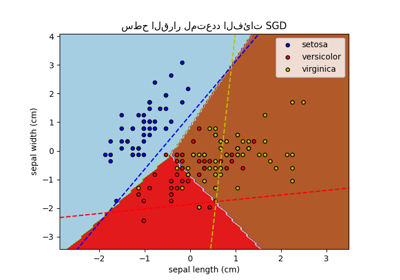
مقارنة بين الإسقاط ثنائي الأبعاد للمجموعة البيانات آيريس باستخدام LDA وPCA
sphx_glr_auto_examples_decomposition_plot_incremental_pca.py
رسم سطح القرار لأشجار القرار المدربة على مجموعة بيانات الزهرة الآرغوانية