ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

Kernel PCA#

يوضح هذا المثال الفرق بين تحليل المكونات الرئيسية (PCA) ونسخته المطبقة مع النواة (KernelPCA).

من ناحية، نوضح أن KernelPCA قادر على إيجاد إسقاط للبيانات يفصلها خطيًا بينما لا يكون هذا هو الحال مع PCA.

أخيرًا، نوضح أن عكس هذا الإسقاط هو تقريب مع KernelPCA، بينما يكون دقيقًا مع PCA.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

مشروع البيانات: `PCA` مقابل. `KernelPCA`#

في هذا القسم، نوضح مزايا استخدام نواة عند مشروع البيانات باستخدام تحليل المكونات الرئيسية (PCA). ننشئ مجموعة بيانات مكونة من دائرتين متداخلتين.

from sklearn.decomposition import PCA, KernelPCA
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

X, y = make_circles(n_samples=1_000, factor=0.3, noise=0.05, random_state=0)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, stratify=y, random_state=0)

لنلقِ نظرة سريعة على مجموعة البيانات المولدة.

_, (train_ax, test_ax) = plt.subplots(
    ncols=2, sharex=True, sharey=True, figsize=(8, 4))

train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train)
train_ax.set_ylabel("الميزة #1")
train_ax.set_xlabel("الميزة #0")
train_ax.set_title("بيانات التدريب")

test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
test_ax.set_xlabel("الميزة #0")
_ = test_ax.set_title("بيانات الاختبار")

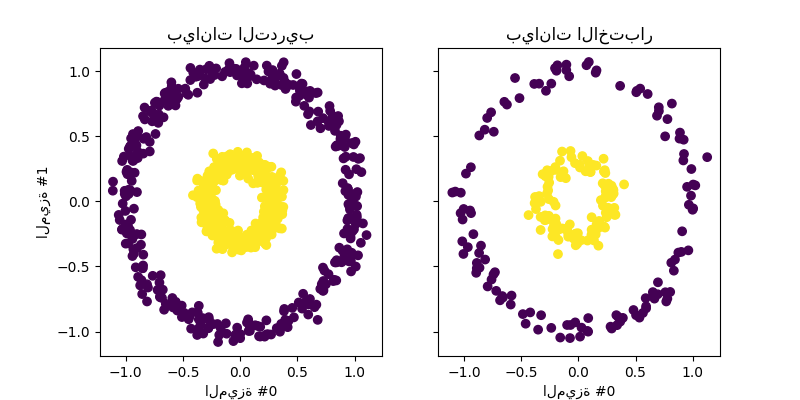
لا يمكن فصل العينات من كل فئة بشكل خطي: لا يوجد خط مستقيم يمكنه تقسيم عينات المجموعة الداخلية من المجموعة الخارجية مجموعة.

الآن، سنستخدم PCA مع وبدون نواة لمعرفة تأثير استخدام مثل هذه النواة. النواة المستخدمة هنا هي وظيفة أساس شعاعي (RBF) نواة.

pca = PCA(n_components=2)
kernel_pca = KernelPCA(
    n_components=None, kernel="rbf", gamma=10, fit_inverse_transform=True, alpha=0.1
)

X_test_pca = pca.fit(X_train).transform(X_test)
X_test_kernel_pca = kernel_pca.fit(X_train).transform(X_test)

fig, (orig_data_ax, pca_proj_ax, kernel_pca_proj_ax) = plt.subplots(
    ncols=3, figsize=(14, 4)
)

orig_data_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
orig_data_ax.set_ylabel("الميزة #1")
orig_data_ax.set_xlabel("الميزة #0")
orig_data_ax.set_title("بيانات الاختبار")

pca_proj_ax.scatter(X_test_pca[:, 0], X_test_pca[:, 1], c=y_test)
pca_proj_ax.set_ylabel("المكون الرئيسي #1")
pca_proj_ax.set_xlabel("المكون الرئيسي #0")
pca_proj_ax.set_title("مشروع بيانات الاختبار\n باستخدام PCA")

kernel_pca_proj_ax.scatter(
    X_test_kernel_pca[:, 0], X_test_kernel_pca[:, 1], c=y_test)
kernel_pca_proj_ax.set_ylabel("المكون الرئيسي #1")
kernel_pca_proj_ax.set_xlabel("المكون الرئيسي #0")
_ = kernel_pca_proj_ax.set_title("مشروع بيانات الاختبار\n باستخدام KernelPCA")

بيانات الاختبار, مشروع بيانات الاختبار باستخدام PCA, مشروع بيانات الاختبار باستخدام KernelPCA

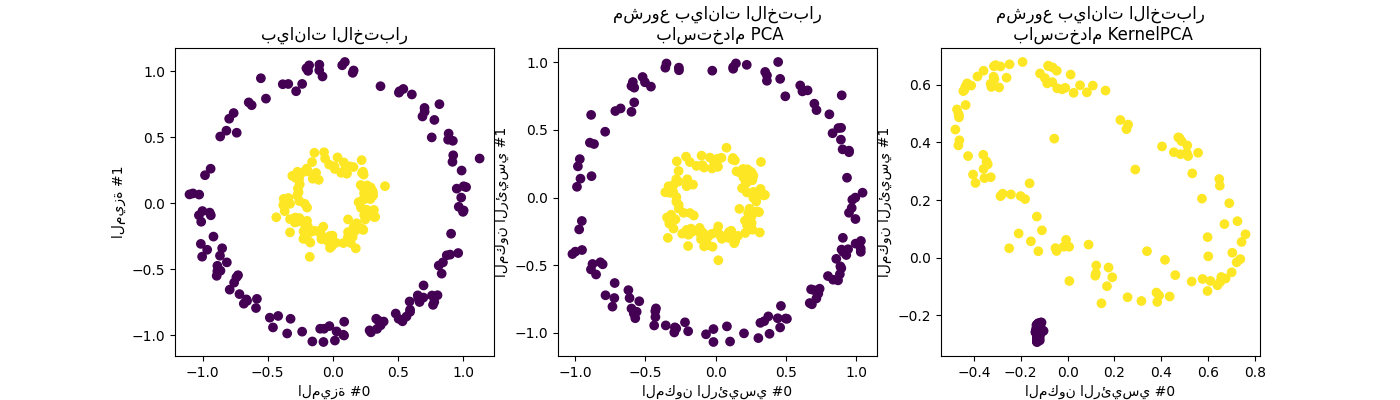
نذكر أن PCA يحول البيانات خطيًا. بشكل حدسي، يعني ذلك أن سيتم تركز نظام الإحداثيات، وإعادة تحجيم كل مكون فيما يتعلق بتغيره وأخيرًا يتم تدويره. البيانات التي يتم الحصول عليها من هذه التحويلة متساوية الاتجاه ويمكن الآن يتم عرضها على المكونات الرئيسية.

وبالتالي، عند النظر إلى المشروع الذي تم إجراؤه باستخدام PCA (أي الشكل الأوسط)، فإننا نرى أنه لا يوجد تغيير فيما يتعلق بالتحجيم؛ في الواقع، البيانات عبارة عن دائرتان متمركزتان في الصفر، والبيانات الأصلية متساوية الاتجاه بالفعل. ومع ذلك، يمكننا أن نرى أن البيانات قد تم تدويرها. كـ استنتاج، نرى أن مثل هذا المشروع لن يساعد إذا حددنا مصنفًا خطيًا للتمييز عينات من كلتا الفئتين.

يسمح استخدام النواة بإجراء مشروع غير خطي. هنا، باستخدام نواة RBF نتوقع أن المشروع سيكشف مجموعة البيانات مع الحفاظ تقريبًا الحفاظ على المسافات النسبية لزوج من نقاط البيانات قريبة من بعضها البعض في الفضاء الأصلي.

نلاحظ مثل هذا السلوك في الشكل على اليمين: عينات فئة معينة أقرب إلى بعضها البعض من عينات الفئة المعاكسة، فك كلا مجموعتي العينات. الآن، يمكننا استخدام مصنف خطي لفصل العينات من الفئتين.

المشروع في مساحة الميزة الأصلية#

إحدى الخصوصيات التي يجب مراعاتها عند استخدام KernelPCA تتعلق بإعادة البناء (أي العرض الخلفي في مساحة الميزة الأصلية). مع PCA، ستكون إعادة البناء دقيقة إذا n_components هو نفسه عدد الميزات الأصلية. هذه هي الحالة في هذا المثال.

يمكننا التحقيق إذا حصلنا على مجموعة البيانات الأصلية عند العرض الخلفي مع KernelPCA.

X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test))
X_reconstructed_kernel_pca = kernel_pca.inverse_transform(
    kernel_pca.transform(X_test))

fig, (orig_data_ax, pca_back_proj_ax, kernel_pca_back_proj_ax) = plt.subplots(
    ncols=3, sharex=True, sharey=True, figsize=(13, 4)
)

orig_data_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
orig_data_ax.set_ylabel("الميزة #1")
orig_data_ax.set_xlabel("الميزة #0")
orig_data_ax.set_title("بيانات الاختبار الأصلية")

pca_back_proj_ax.scatter(
    X_reconstructed_pca[:, 0], X_reconstructed_pca[:, 1], c=y_test)
pca_back_proj_ax.set_xlabel("الميزة #0")
pca_back_proj_ax.set_title("إعادة البناء عبر PCA")

kernel_pca_back_proj_ax.scatter(
    X_reconstructed_kernel_pca[:,
                               0], X_reconstructed_kernel_pca[:, 1], c=y_test
)
kernel_pca_back_proj_ax.set_xlabel("الميزة #0")
_ = kernel_pca_back_proj_ax.set_title("إعادة البناء عبر KernelPCA")

بيانات الاختبار الأصلية, إعادة البناء عبر PCA, إعادة البناء عبر KernelPCA

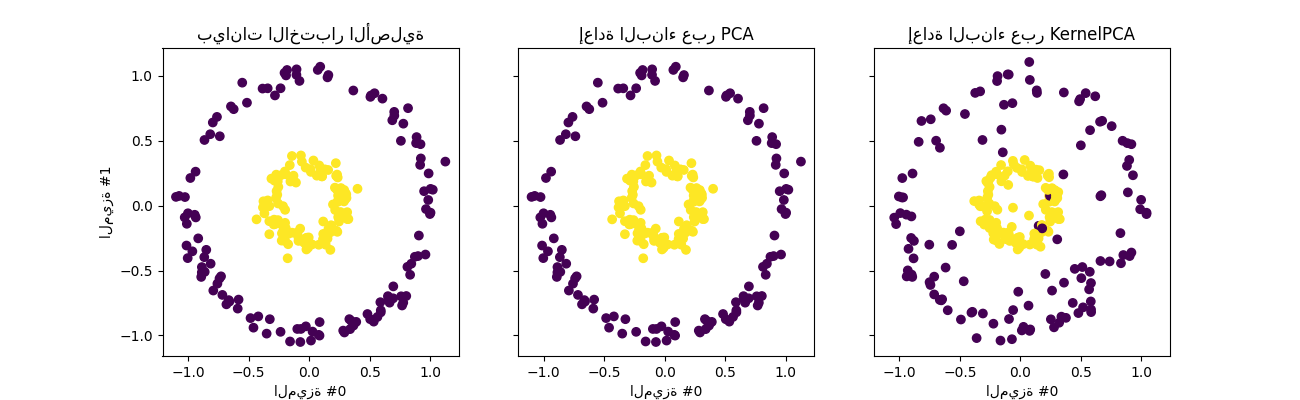
بينما نرى إعادة بناء مثالية مع PCA، نلاحظ نتيجة مختلفة لـ KernelPCA.

في الواقع، لا يمكن لـ inverse_transform الاعتماد على العرض الخلفي التحليلي وبالتالي إعادة البناء الدقيقة. بدلاً من ذلك، يتم تدريب KernelRidge داخليًا لتعلم خريطة من أساس PCA المُكرنل إلى مساحة الميزة الأصلية. لذلك، تأتي هذه الطريقة مع تقريب يقدم اختلافات صغيرة عند العرض الخلفي في مساحة الميزة الأصلية.

لتحسين إعادة البناء باستخدام inverse_transform، يمكن ضبط alpha في KernelPCA، مصطلح التنظيم الذي يتحكم في الاعتماد على بيانات التدريب أثناء تدريب الخريطة.

Total running time of the script: (0 minutes 0.728 seconds)