ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
FastICA على سحب النقاط ثنائية الأبعاد#
يوضح هذا المثال بصريًا في فضاء الميزات مقارنة بالنتائج باستخدام تقنيتين مختلفتين لتحليل المكونات.
تحليل المكونات المستقلة (ICA) مقابل تحليل المكونات الرئيسية (PCA).
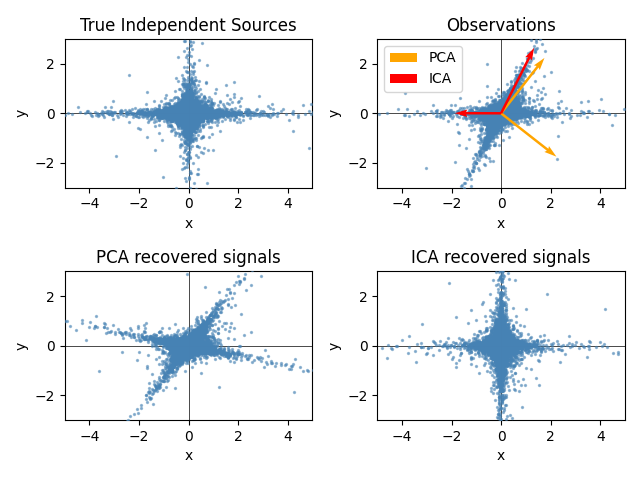
تمثيل ICA في فضاء الميزات يعطي نظرة على 'ICA الهندسي': ICA هو خوارزمية تجد اتجاهات في فضاء الميزات المرتبطة بالانحرافات ذات اللاغاوسية العالية. هذه الاتجاهات لا تحتاج إلى أن تكون متعامدة في فضاء الميزات الأصلي، ولكنها متعامدة في فضاء الميزات المبيض، حيث ترتبط جميع الاتجاهات بنفس التباين.
PCA، من ناحية أخرى، يجد اتجاهات متعامدة في فضاء الميزات الخام التي ترتبط باتجاهات تحسب التباين الأقصى.
هنا، نقوم بمحاكاة مصادر مستقلة باستخدام عملية غير غاوسية للغاية، 2 طالب T مع عدد منخفض من درجات الحرية (الشكل العلوي الأيسر). نقوم بمزجها لإنشاء الملاحظات (الشكل العلوي الأيمن). في هذا الفضاء الخام للملاحظات، يتم تمثيل الاتجاهات التي حددتها PCA بواسطة المتجهات البرتقالية. نمثل الإشارة في فضاء PCA، بعد التبييض بواسطة التباين المقابل للمتجهات PCA (الأسفل اليسار). تشغيل ICA يقابل إيجاد دوران في هذا الفضاء لتحديد اتجاهات اللاغاوسية القصوى (الأسفل الأيمن).
# المؤلفون: مطوري سكايت-ليرن
# معرف SPDX-License: BSD-3-Clause
توليد بيانات العينة#
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA, FastICA
rng = np.random.RandomState(42)
S = rng.standard_t(1.5, size=(20000, 2))
S[:, 0] *= 2.0
# مزج البيانات
A = np.array([[1, 1], [0, 2]]) # مصفوفة المزج
X = np.dot(S, A.T) # توليد الملاحظات
pca = PCA()
S_pca_ = pca.fit(X).transform(X)
ica = FastICA(random_state=rng, whiten="arbitrary-variance")
S_ica_ = ica.fit(X).transform(X) # تقدير المصادر
رسم النتائج#
def plot_samples(S, axis_list=None):
plt.scatter(
S[:, 0], S[:, 1], s=2, marker="o", zorder=10, color="steelblue", alpha=0.5
)
if axis_list is not None:
for axis, color, label in axis_list:
x_axis, y_axis = axis / axis.std()
plt.quiver(
(0, 0),
(0, 0),
x_axis,
y_axis,
zorder=11,
width=0.01,
scale=6,
color=color,
label=label,
)
plt.hlines(0, -5, 5, color="black", linewidth=0.5)
plt.vlines(0, -3, 3, color="black", linewidth=0.5)
plt.xlim(-5, 5)
plt.ylim(-3, 3)
plt.gca().set_aspect("equal")
plt.xlabel("x")
plt.ylabel("y")
plt.figure()
plt.subplot(2, 2, 1)
plot_samples(S / S.std())
plt.title("True Independent Sources")
axis_list = [(pca.components_.T, "orange", "PCA"), (ica.mixing_, "red", "ICA")]
plt.subplot(2, 2, 2)
plot_samples(X / np.std(X), axis_list=axis_list)
legend = plt.legend(loc="upper left")
legend.set_zorder(100)
plt.title("Observations")
plt.subplot(2, 2, 3)
plot_samples(S_pca_ / np.std(S_pca_))
plt.title("PCA recovered signals")
plt.subplot(2, 2, 4)
plot_samples(S_ica_ / np.std(S_ica_))
plt.title("ICA recovered signals")
plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.36)
plt.tight_layout()
plt.show()
Total running time of the script: (0 minutes 0.443 seconds)
Related examples
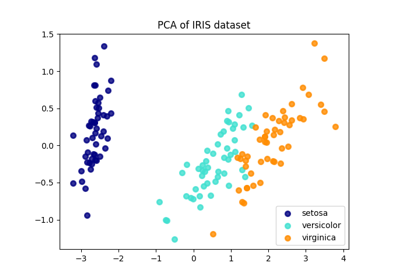
مقارنة بين الإسقاط ثنائي الأبعاد للمجموعة البيانات آيريس باستخدام LDA وPCA
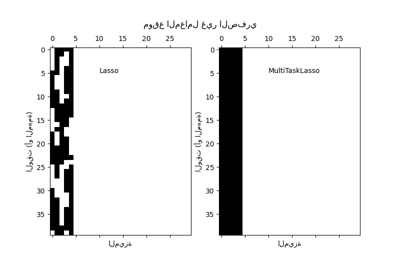
الاختيار المشترك للميزات باستخدام Lasso متعدد المهام