ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

مقارنة بين الإسقاط ثنائي الأبعاد للمجموعة البيانات آيريس باستخدام LDA وPCA#

تمثل مجموعة بيانات آيريس 3 أنواع من زهور آيريس (سيتوسا، وفيرسيكولور، وفيرجينيكا) مع 4 خصائص: طول الكأس، وعرض الكأس، وطول البتلة، وعرض البتلة.

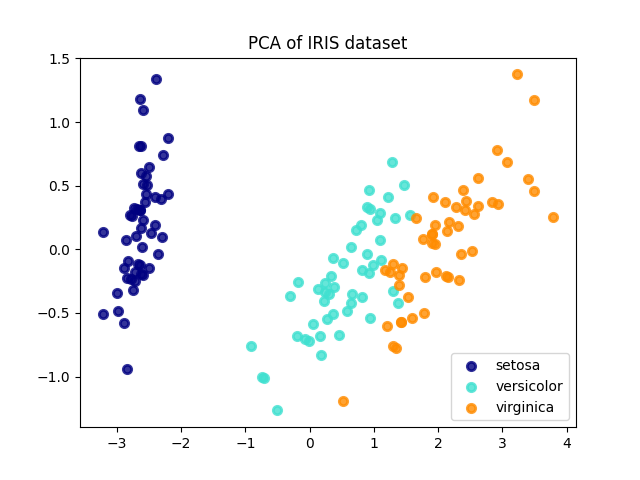
تحدد تحليل المكونات الرئيسية (PCA) المطبق على هذه البيانات مجموعة الخصائص (المكونات الرئيسية، أو الاتجاهات في فضاء الميزات) التي تفسر معظم التباين في البيانات. هنا نرسم العينات المختلفة على أول مكونين رئيسيين.

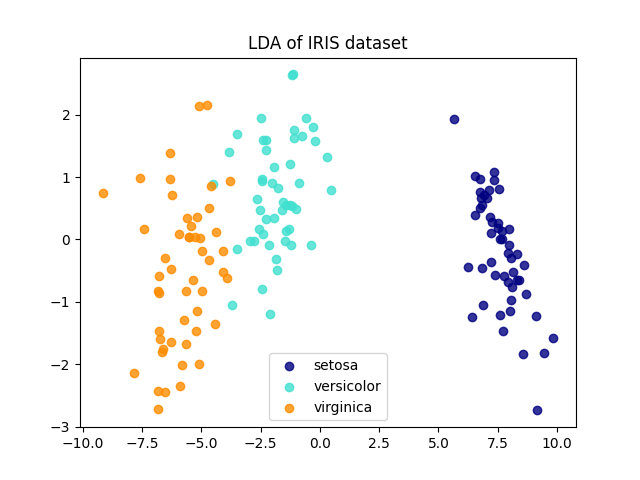
يحاول تحليل التمييز الخطي (LDA) تحديد الخصائص التي تفسر معظم التباين بين الفئات. وعلى وجه الخصوص، فإن LDA، على عكس PCA، هي طريقة مُشرفة تستخدم تسميات الفئات المعروفة.

explained variance ratio (first two components): [0.92461872 0.05306648]

# المؤلفون: مطوري سكايت-ليرن
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris = datasets.load_iris()

X = iris.data
y = iris.target
target_names = iris.target_names

pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)

lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)

# نسبة التباين الموضحة لكل مكون
print(
    "explained variance ratio (first two components): %s"
    % str(pca.explained_variance_ratio_)
)

plt.figure()
colors = ["navy", "turquoise", "darkorange"]
lw = 2

for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(
        X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=0.8, lw=lw, label=target_name
    )
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("PCA of IRIS dataset")

plt.figure()
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(
        X_r2[y == i, 0], X_r2[y == i, 1], alpha=0.8, color=color, label=target_name
    )
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("LDA of IRIS dataset")

plt.show()