ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
مسارات لاصو ولاصو-لارس وشبكة مرنة#
هذا المثال يوضح كيفية حساب "المسارات" لمعاملات لاصو، لاصو-لارس، ومسارات الشبكة المرنة. وبعبارة أخرى، فإنه يظهر العلاقة بين معامل التنظيم (ألفا) والمعاملات.
يفرض لاصو ولاصو-لارس قيدًا على المعاملات، تشجيع بعضها على أن تكون صفرًا. الشبكة المرنة هي تعميم لاصو الذي يضيف مصطلح عقوبة L2 إلى مصطلح عقوبة L1. هذا يسمح لبعض المعاملات أن تكون غير صفرية مع تشجيع التباعد.
يستخدم لاصو والشبكة المرنة طريقة النزول المنسق لحساب المسارات، في حين يستخدم لاصو-لارس خوارزمية لارس لحساب المسارات.
يتم حساب المسارات باستخدام: func:~sklearn.linear_model.lasso_path،
lars_path، و:func:~sklearn.linear_model.enet_path.
تظهر النتائج مخططات مقارنة مختلفة:
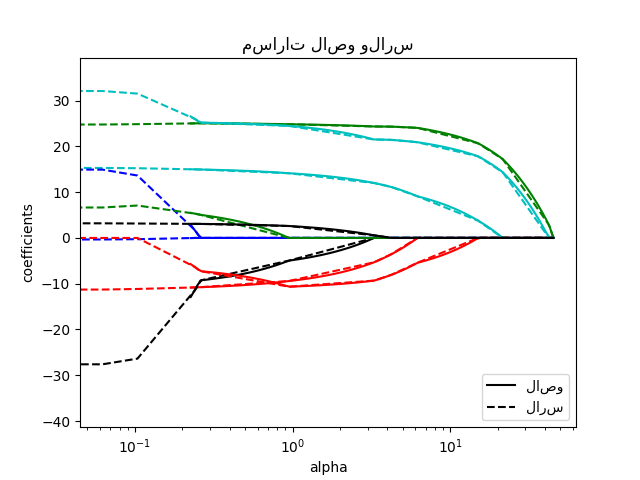
مقارنة لاصو ولاصو-لارس
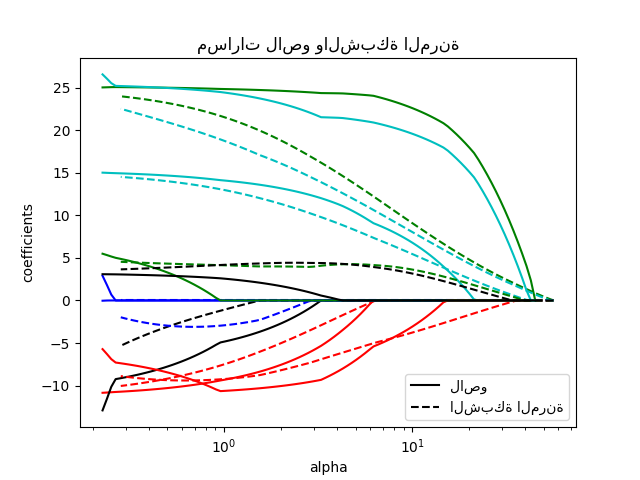
مقارنة لاصو والشبكة المرنة
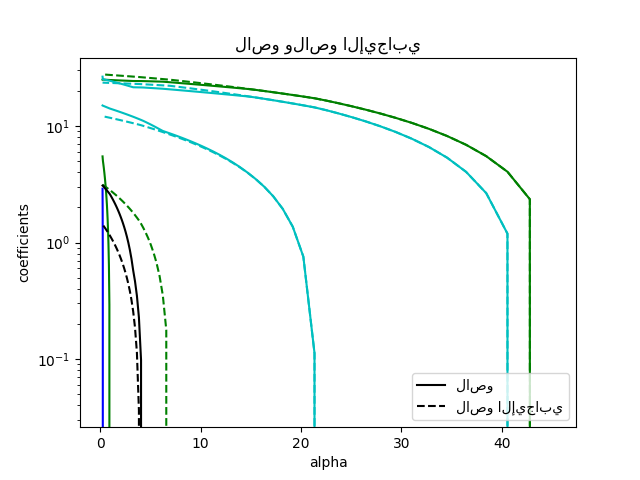
مقارنة لاصو مع لاصو الإيجابي
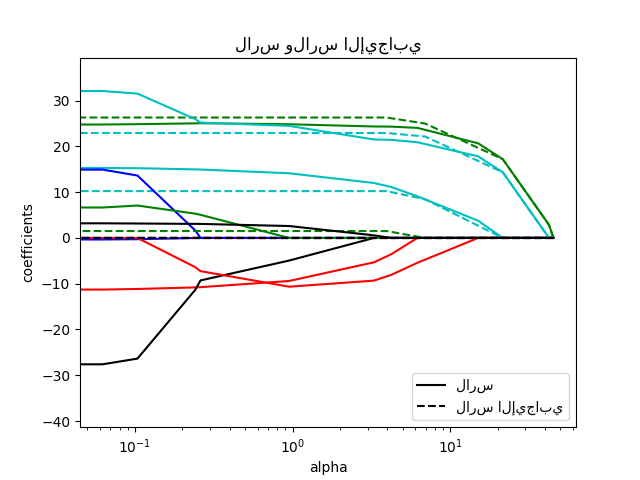
مقارنة لارس ولارس الإيجابي
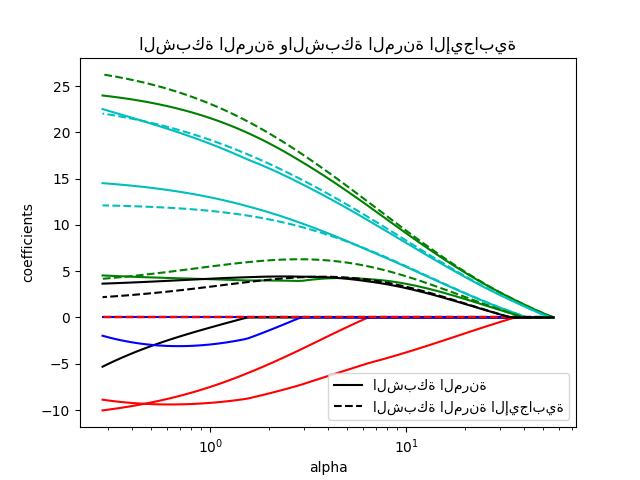
مقارنة الشبكة المرنة والشبكة المرنة الإيجابية
يظهر كل رسم بياني كيف تختلف معاملات النموذج مع تغير قوة التنظيم، تقديم نظرة ثاقبة لسلوك هذه النماذج تحت قيود مختلفة.
حساب مسار التنظيم باستخدام لاصو...
حساب مسار التنظيم باستخدام لاصو الإيجابي...
حساب مسار التنظيم باستخدام لارس...
حساب مسار التنظيم باستخدام لارس الإيجابي...
حساب مسار التنظيم باستخدام الشبكة المرنة...
حساب مسار التنظيم باستخدام الشبكة المرنة الإيجابية...
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
from itertools import cycle
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.linear_model import enet_path, lars_path, lasso_path
X, y = load_diabetes(return_X_y=True)
X /= X.std(axis=0) # توحيد البيانات (أسهل في تعيين معامل l1_ratio)
# حساب المسارات
eps = 5e-3 # كلما صغر، كلما طال المسار
print("حساب مسار التنظيم باستخدام لاصو...")
alphas_lasso, coefs_lasso, _ = lasso_path(X, y, eps=eps)
print("حساب مسار التنظيم باستخدام لاصو الإيجابي...")
alphas_positive_lasso, coefs_positive_lasso, _ = lasso_path(
X, y, eps=eps, positive=True
)
print("حساب مسار التنظيم باستخدام لارس...")
alphas_lars, _, coefs_lars = lars_path(X, y, method="lasso")
print("حساب مسار التنظيم باستخدام لارس الإيجابي...")
alphas_positive_lars, _, coefs_positive_lars = lars_path(
X, y, method="lasso", positive=True
)
print("حساب مسار التنظيم باستخدام الشبكة المرنة...")
alphas_enet, coefs_enet, _ = enet_path(X, y, eps=eps, l1_ratio=0.8)
print("حساب مسار التنظيم باستخدام الشبكة المرنة الإيجابية...")
alphas_positive_enet, coefs_positive_enet, _ = enet_path(
X, y, eps=eps, l1_ratio=0.8, positive=True
)
# عرض النتائج
plt.figure(1)
colors = cycle(["b", "r", "g", "c", "k"])
for coef_lasso, coef_lars, c in zip(coefs_lasso, coefs_lars, colors):
l1 = plt.semilogx(alphas_lasso, coef_lasso, c=c)
l2 = plt.semilogx(alphas_lars, coef_lars, linestyle="--", c=c)
plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("مسارات لاصو ولارس")
plt.legend((l1[-1], l2[-1]), ("لاصو", "لارس"), loc="lower right")
plt.axis("tight")
plt.figure(2)
colors = cycle(["b", "r", "g", "c", "k"])
for coef_l, coef_e, c in zip(coefs_lasso, coefs_enet, colors):
l1 = plt.semilogx(alphas_lasso, coef_l, c=c)
l2 = plt.semilogx(alphas_enet, coef_e, linestyle="--", c=c)
plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("مسارات لاصو والشبكة المرنة")
plt.legend((l1[-1], l2[-1]), ("لاصو", "الشبكة المرنة"), loc="lower right")
plt.axis("tight")
plt.figure(3)
for coef_l, coef_pl, c in zip(coefs_lasso, coefs_positive_lasso, colors):
l1 = plt.semilogy(alphas_lasso, coef_l, c=c)
l2 = plt.semilogy(alphas_positive_lasso, coef_pl, linestyle="--", c=c)
plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("لاصو ولاصو الإيجابي")
plt.legend((l1[-1], l2[-1]), ("لاصو", "لاصو الإيجابي"), loc="lower right")
plt.axis("tight")
plt.figure(4)
colors = cycle(["b", "r", "g", "c", "k"])
for coef_lars, coef_positive_lars, c in zip(coefs_lars, coefs_positive_lars, colors):
l1 = plt.semilogx(alphas_lars, coef_lars, c=c)
l2 = plt.semilogx(alphas_positive_lars, coef_positive_lars, linestyle="--", c=c)
plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("لارس ولارس الإيجابي")
plt.legend((l1[-1], l2[-1]), ("لارس", "لارس الإيجابي"), loc="lower right")
plt.axis("tight")
plt.figure(5)
for coef_e, coef_pe, c in zip(coefs_enet, coefs_positive_enet, colors):
l1 = plt.semilogx(alphas_enet, coef_e, c=c)
l2 = plt.semilogx(alphas_positive_enet, coef_pe, linestyle="--", c=c)
plt.xlabel("alpha")
plt.ylabel("coefficients")
plt.title("الشبكة المرنة والشبكة المرنة الإيجابية")
plt.legend((l1[-1], l2[-1]), ("الشبكة المرنة", "الشبكة المرنة الإيجابية"), loc="lower right")
plt.axis("tight")
plt.show()
Total running time of the script: (0 minutes 0.957 seconds)
Related examples
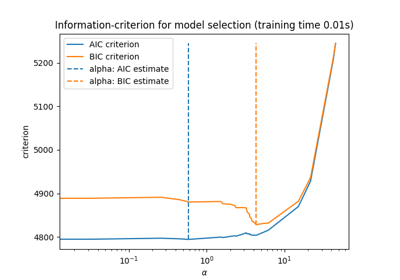
نموذج لاصو: اختيار النموذج باستخدام معايير AIC-BIC والتحقق المتقاطع